AP Board 7th Class Maths Solutions Chapter 10 త్రిభుజాల నిర్మాణం InText Questions

SCERT AP 7th Class Maths Solutions Pdf Chapter 10 త్రిభుజాల నిర్మాణం InText Questions and Answers.

AP State Syllabus 7th Class Maths Solutions 10th Lesson త్రిభుజాల నిర్మాణం InText Questions

[పేజీ నెం. 134]

ప్రక్క చిత్రమును చూసి, ప్రశ్నలకు సమాధానం ఇవ్వండి:

ప్రశ్న 1.
మీ నిత్యజీవితంలో త్రిభుజాకారంలో ఉన్న కొన్ని వస్తువుల పేర్లు తెలపండి.
జవాబు
సమోసా, చపాతి, ఇంటి పైకప్పు, వంతెన ట్రస్సులు, భవనం టెస్సెలేషన్స్,

ప్రశ్న 2.
చిత్రంలో కనపడు త్రిభుజాల రకాలు ఏవి?
జవాబు
లంబకోణ త్రిభుజాలు, సమబాహు త్రిభుజాలు.

ప్రశ్న 3.
అన్ని త్రిభుజాలు వాటి ధర్మాలననుసరించి ఒకేరకంగా కనిపిస్తున్నాయని అనుకుంటున్నారా ? అవి ఏవి ?
జవాబు
అవును. అన్ని త్రిభుజాలు ఒకే రకంగా కనిపిస్తున్నాయి. ఎందువలననగా ఆ త్రిభుజాలు
(a) లంబకోణం
(b) సమాన భుజం మరియు
(c) సమాన కర్ణం కలిగి ఉంటాయి.

నీ ప్రగతిని సరిచూసుకో [పేజి నెం. 138]

ప్రశ్న 1.
XY = 4 సెం.మీ ఉండునట్లు సమబాహు త్రిభుజం ∆XYZను నిర్మించండి.
సాధన.

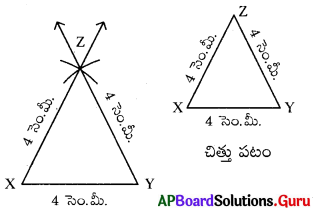
నిర్మాణ సోపానక్రమం:

1. చిత్తు పటాన్ని గీచి, కొలతలను గుర్తించాలి.
2. XY = 4 సెం.మీ.లతో రేఖాఖండాన్ని గీయాలి.
3. ‘X’ కేంద్రంగా 4 సెం.మీ. వ్యాసార్ధంతో ఒక చాపరేఖ గీయాలి.
4. ” కేంద్రంగా 4 సెం.మీ. వ్యాసార్ధంతో పై చాపరేఖను ఖండిస్తూ మరొక చాపరేఖను గీయాలి. ఖండన బిందువును ‘Z’ గా గుర్తించాలి.
5. XZ, YZ లను కలపాలి. మనకు కావలసిన ∆XYZ ఏర్పడినది.

ప్రశ్న 2.
PQ = PR = 3 సెం.మీ, QR = 5 సెం.మీ కొలతలతో సమద్విబాహు త్రిభుజం ∆PQR ను నిర్మించండి.
సాధన.

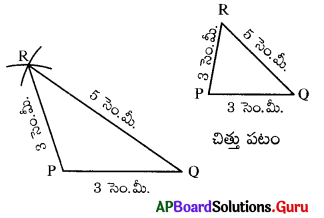
నిర్మాణ సోపానక్రమం:

1. చిత్తు పటంను గీచి, ఇచ్చిన కొలతలను గుర్తించాలి.
2. PQ = 3 సెం.మీ.లతో రేఖాఖండాన్ని గీయాలి.
3. P కేంద్రంగా 3 సెం.మీ. వ్యాసార్ధంతో ఒక చాపరేఖను గీయాలి.
4. Q కేంద్రంగా 5 సెం.మీ. వ్యాసార్థంతో పై చాపరేఖను ఖండిస్తూ మరొక. చాపరేఖను గీచి, ఖండన బిందువును R గా గుర్తించాలి.
5. PR, QR లను కలపాలి. మనకు కావలసిన ∆POR ఏర్పడినది.

ఆలోచించండి [పేజి నెం. 138]

AB = 4 సెం.మీ., BC = 5 సెం.మీ. మరియు CA = 10 సెం.మీ. కొలతలతో ∆ABC ను నిర్మించగలమా?
సాధన.
AB = 4. సెం.మీ., BC = 5 సెం.మీ. మరియు CA = 10 సెం.మీ.
ఒక త్రిభుజంలో ఏ రెండు భుజాల మొత్తమయినా, మూడవ భుజం కన్నా ఎక్కువ ఉండాలి.
AB + BC = 4 సెం.మీ. + 5 సెం.మీ.
= 9 సెం.మీ. < 10 సెం.మీ.
AB + BC < AC
కావున, ఇవ్వబడిన కొలతలు ∆ABC త్రిభుజాన్ని ఏర్పరచవు.

నీ ప్రగతిని సరిచూసుకో [పేజి నెం. 144]

ప్రశ్న 1.
MA = 5.5 సెం.మీ., MT = 4 సెం.మీ. మరియు ∠M = 70° కొలతలతో త్రిభుజం MATని గీయండి.
సాధన.

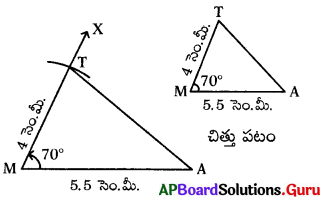
నిర్మాణ సోపానక్రమం:

1. చిత్తుపటాన్ని గీచి, ఇచ్చిన కొలతలను గుర్తించాలి.
2. MA = 5.5 సెం.మీ.లతో ఒక రేఖాఖండాన్ని గీయాలి.
3. ∠AMX = 70° ఉండునట్లు MT కిరణాన్ని గీయాలి.
4. M కేంద్రంగా 4 సెం.మీ. వ్యాసార్ధంతో \(\overrightarrow{\mathrm{MT}}\) పై
   ఒక చాపరేఖను గీచి, ఖండన బిందువును T గా గుర్తించాలి.
5. AT లను కలుపగా మనకు కావలసిన త్రిభుజం ∆MAT ఏర్పడినది.

అన్వేషిద్దాం [పేజి నెం. 144]

ప్రశ్న 1.
AB = 7 సెం.మీ., ∠B = 60° మరియు ∠C = 70° కొలతలతో త్రిభుజాన్ని నిర్మించండి.
సాధన.
AB = 7 సెం.మీ. ఇవ్వడం వలన మనకు ∠A, ∠B కోణాల విలువ తెలిసినపుడు త్రిభుజాన్ని గీయగలము. అయితే ∠A విలువ ఇవ్వలేదు. అయితే ∠B = 60°, ∠C = 70° ఇవ్వడం జరిగినది. ఈ కోణాల సహాయంతో మనం ∠A ను కనుగొని, తర్వాత నిర్మాణం పూర్తి చేయాలి.
∆ABC లో
∠A + ∠B + ∠C = 180°
∠A + 60° + 70° = 180°
∠A + 130° = 180°
∴ ∠A = 180° – 130°
∴ ∠A = 50°

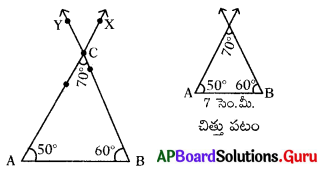
నిర్మాణ సోపానక్రమం:

1. చిత్తుపటాన్ని గీచి, ఇచ్చిన కొలతలను గుర్తించాలి.
2. ∠A = 50° ఉండునట్లు \(\overrightarrow{\mathrm{AX}}\) ని గీయాలి.
3. ∠B = 60° ఉండునట్లు \(\overrightarrow{\mathrm{BY}}\) ని గీయాలి. రెండింటి ఖండన బిందువును ‘C’ గా గుర్తించాలి.
4. మనకు కావలసిన ∆ABC ఏర్పడినది.

నీ ప్రగతిని సరిచూసుకో [పేజి నెం. 146]

ప్రశ్న 1.
∠A = 90°, ∠C = 50° మరియు AC = 8 సెం.మీ. కొలతలతో ∆ABCని నిర్మించండి.
సాధన.

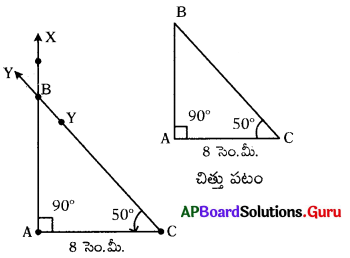
నిర్మాణ సోపానక్రమం :

1. చిత్తుపటాన్ని గీచి, ఇచ్చిన కొలతలను గుర్తించాలి.
2. AC = 8 సెం.మీ. లతో ఒక రేఖాఖండాన్ని గీయాలి.
3. ∠A = 90° లతో ఒక AX కిరణాన్ని గీయాలి.
4. ∠C = 50° లతో ఒక CY కిరణాన్ని గీయాలి.
   ఈ రెండు కిరణాల ఖండన బిందువును B గా గుర్తించాలి.
5. మనకు కావలసిన లంబకోణ త్రిభుజం ∆ABC ఏర్పడినది.

ఆలోచించండి [పేజి నెం. 146]

100°, 95° కోణాల కొలతలు మరియు నీకు నచ్చిన భుజం కొలతతో త్రిభుజాన్ని నిర్మించగలమా?
సాధన.
100°, 95°
కోణాల కొలతలు మరియు ఇచ్చిన భుజం కొలతతో త్రిభుజాన్ని నిర్మించలేము.
కారణం: ఇచ్చిన కోణాల మొత్తం = 100° + 95° = 195°
కాని త్రిభుజంలోని కోణాల మొత్తం 180°.

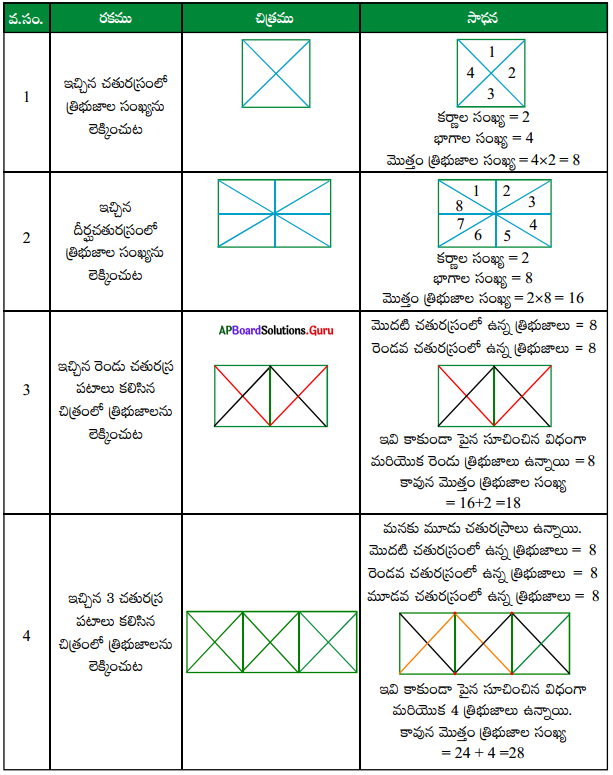
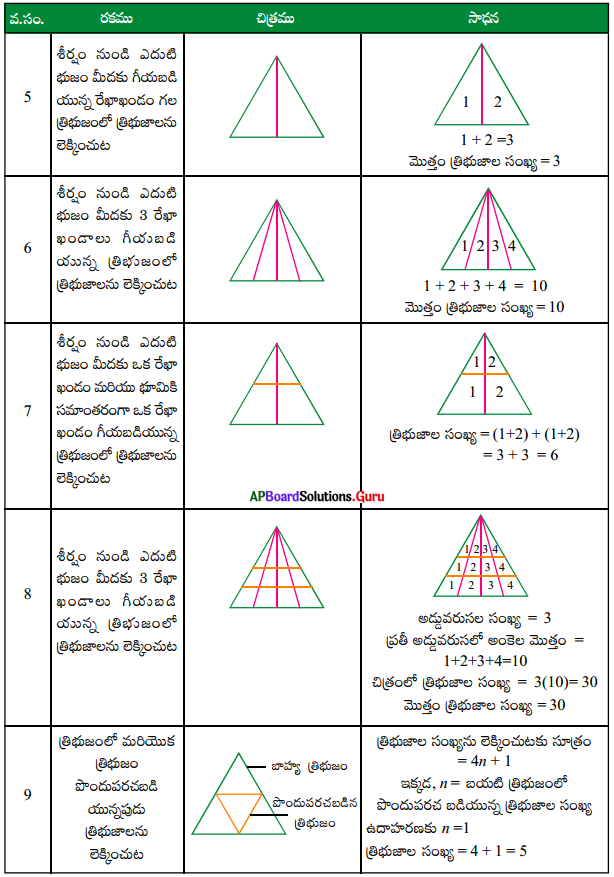
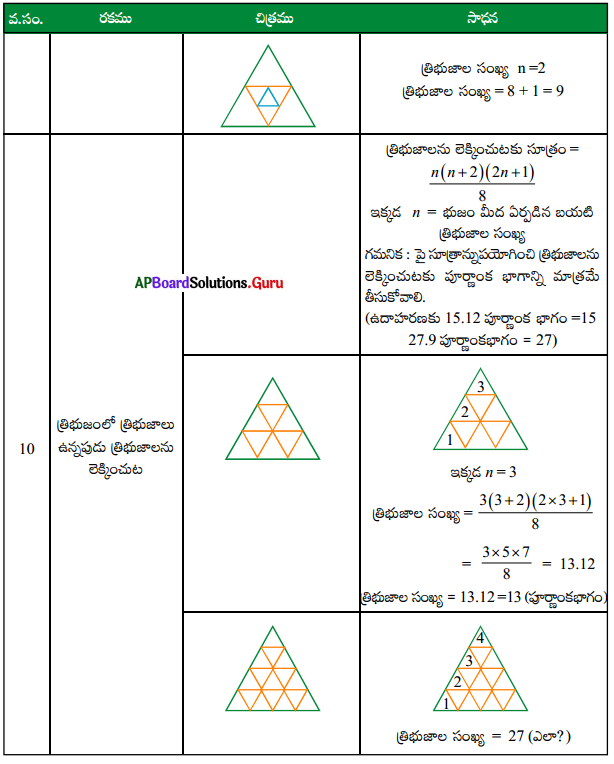
తార్కిక విభాగం త్రిభుజాలను లెక్కించడం [పేజి నెం. 150]

ఉదాహరణ

ప్రశ్న 1.
AB = 6 సెం.మీ, BC = 4 సెం.మీ మరియు AC = 5 సెం.మీ భుజాలుగా గల ∆ABC లను గీయండి.
సాధన.

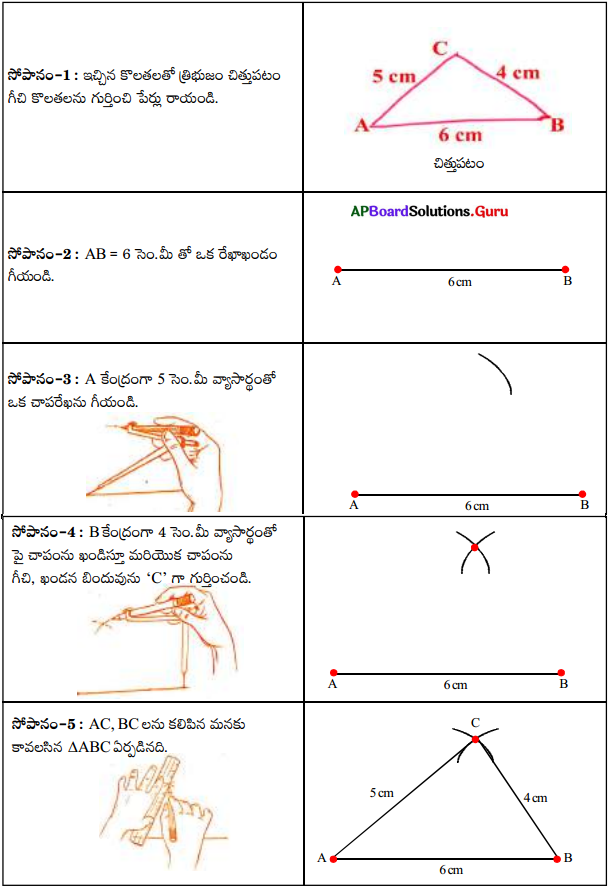
ప్రశ్న 2.
∠F = 70°, EF = 4 సెం.మీ. మరియు FD = 5 సెం.మీ. కొలతలతో ∆EFD ను నిర్మించండి.
సాధన.

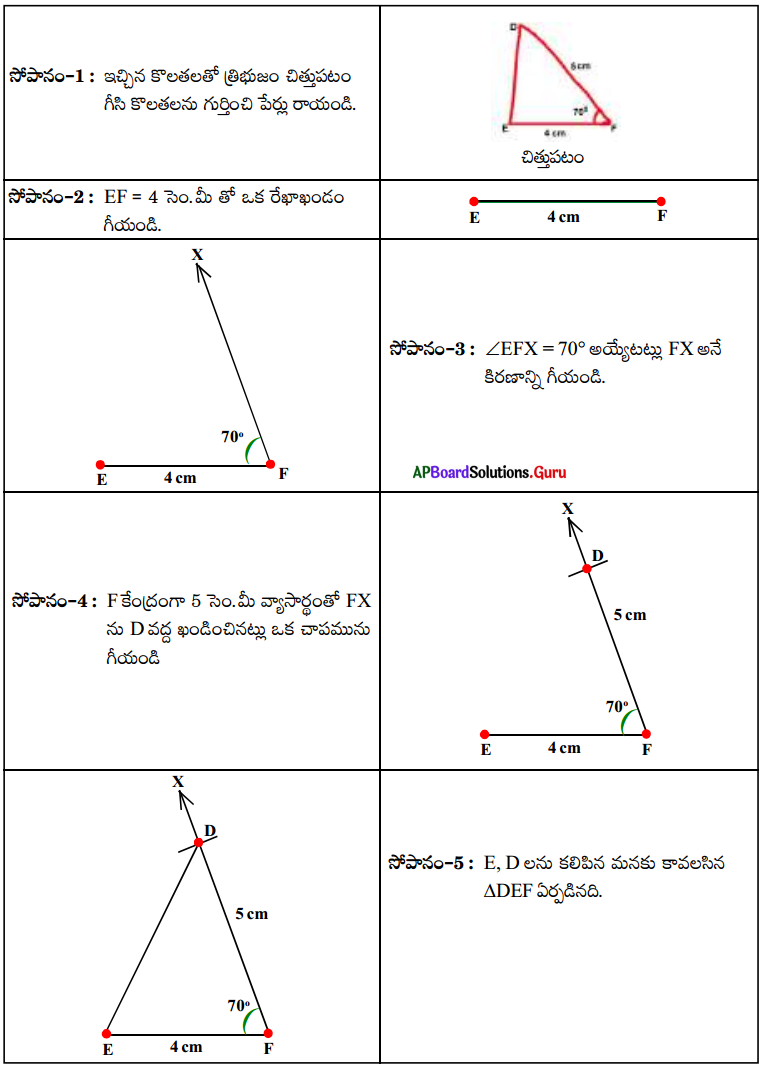
ప్రశ్న 3.
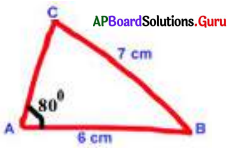
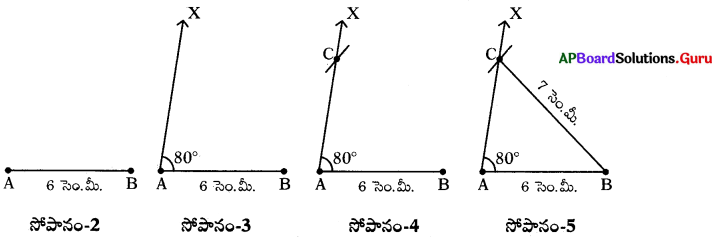
AB = 6 సెం.మీ, BC = 1 సెం.మీ, ∠BAC = 80° కొలతలతో ∆ABC ని నిర్మించండి.
సాధన.
సోపానం-1: ∆ABC చిత్తుపటమును గీచి కొలతలు గుర్తించి పేర్లు రాయండి.
సోపానం-2: AB = 6 సెం.మీ ఉండునట్లు రేఖాఖండం గీయండి.
సోపానం-3: ∠BAX = 80° ఉండునట్లు ఒక కిరణం AX ను గీయండి.
సోపానం-4: B కేంద్రంగా 7 సెం.మీ వ్యాసార్ధంతో AX కిరణమును C వద్ద ఖండించునట్లు ఒక చాపరేఖను గీయండి.
సోపానం-5: B, C లను కలిపిన మనకు కావల్సిన త్రిభుజం ∆ABC ఏర్పడినది.

ప్రశ్న 4.
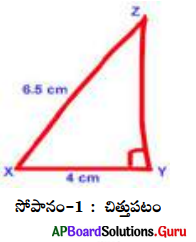
XY = 4 సెం.మీ, XZ = 6.5 సెం.మీ మరియు ∠Y= 90°ల కొలతలతో లంబకోణ త్రిభుజం ∆XYZ గీయండి.
సాధన.
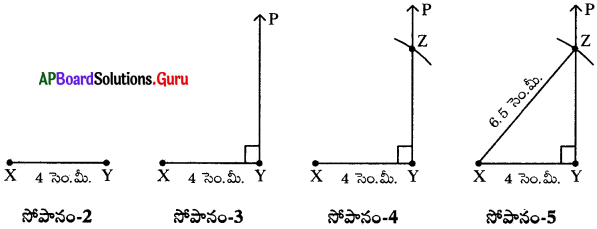
సోపానం-1: ∆XYZ చిత్తుపటం గీసి, కొలతలను గుర్తించి పేర్లు రాయండి.
సోపానం-2: XY = 4 సెం.మీ ఉండేటట్లు ఒక రేఖాఖండమును గీయండి.
సోపానం-3: ∠XYP = 90° ఉండేటట్లు YP కిరణమును గీయండి.
సోపానం-4: X కేంద్రంగా 6.5 సెం.మీ వ్యాసార్ధంతో YP కిరణాన్ని Z వద్ద ఖండించునట్లు, ఒక చాపరేఖను గీయండి.
సోపానం-5: X, Z లను కలిపిన మనకు కావల్సిన త్రిభుజం ∆XYZ ఏర్పడినది.

ప్రశ్న 5.
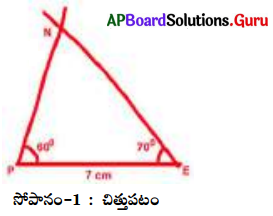
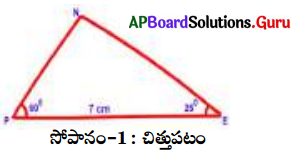
PE = 7 సెం.మీ., ∠PEN = 25° మరియు ∠EPN = 60° కోలతలతో ∆PEN ను గీయండి.
సాధన.
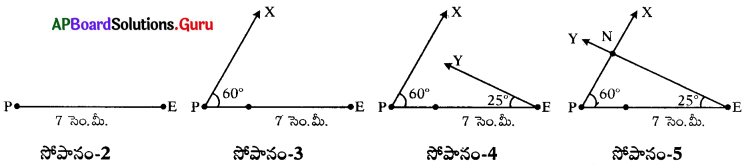
సోపానం-1: ఇచ్చిన కొలతలతో త్రిభుజం చిత్తుపటం గీసి, కొలతలను గుర్తించి పేర్లు రాయండి.
సోపానం-2: PE = 7 సెం.మీ తో ఒక రేఖాఖండం గీయండి.
సోపానం-3: ∠EPX = 60° ఉండునట్లు ఒక కిరణం \(\overrightarrow{\text { PX }}\) ను గీయండి.
సోపానం-4: ∠PEY = 25° ఉండునట్లు మరొక కిరణం \(\overrightarrow{\text { EY }}\) గీయండి.
సోపానం-5: \(\overrightarrow{\text { PX }}\), \(\overrightarrow{\text { EY }}\) కిరణాల ఖండన బిందువును ‘N’ గా గుర్తించండి.
మనకు కావలసిన ∆PEN ఏర్పడినది.
(అవసరమైనచో కిరణాలను ఖండించుకొనునట్లు పొడిగించండి.)

ప్రశ్న 6.
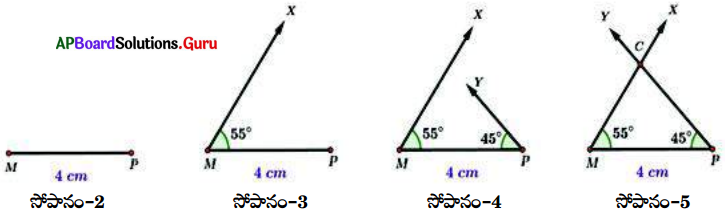
MP = 4 సెం.మీ., ∠P = 45° మరియు ∠C = 80° కొలతలతో ∆MPC ని గీయండి.
సాధన.
ఇప్పుడు, మనం మూడవ కోణాన్ని కనుగొనాలి.
C సోపానం-1 త్రిభుజంలో 3 కోణాల మొత్తం 180° అని మనకు తెలుసు.
కావున, ∠M + ∠P + ∠C = 180°
⇒ ∠M + 45° + 80° = 180°
⇒ ∠M + 125° = 1800
⇒ ∠M = 180° – 125° = 55°

సోపానం-1: ఇచ్చిన కొలతలతో త్రిభుజం చిత్తుపటం గీసి, కొలతలను గీసి, గుర్తించి పేర్లు రాయండి.
సోపానం-2: MP = 4 సెం.మీ తో ఒక రేఖాఖండమును గీయండి.
సోపానం-3: ∠PMX = 55° ఉండునట్లు ఒక కిరణం MX గీయండి.
సోపానం-4: ∠MPY = 45° ఉండునట్లు మరొక కిరణం PY గీయండి.
సోపానం-5: MX, PY కిరణాల ఖండన బిందువును ‘C’ గా గుర్తించండి. (అవసరమైనచో కిరణాలను పొడిగించండి) మనకు కావలసిన ∆MPC ఏర్పడినది.
సరిచూచుట: ∠C కొలత 80° ఉన్నదో లేదో కోణమానిని ఉపయోగించి సరిచూడండి.

సాధనా ప్రశ్నలు [పేజీ నెం. 156]

క్రింద ఇవ్వబడిన పటాలలో ఎన్ని త్రిభుజాలున్నాయో కనుగొనండి.

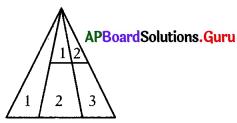
ప్రశ్న 1.

(a) 8
(b) 9
(c) 10
(d) 12
సాధన.
(b) 9

వివరణ:
(i) శీర్షం నుండి ఎదుటి భుజానికి గీచిన రేఖాఖండాలు 2.
కావున ఏర్పడే త్రిభుజాలు 1 + 2 + 3 = 6.
(ii) శీర్షం నుంచి గీచిన రెండు రేఖాఖండాలకు అడ్డంగా భూమికి
సమాంతరంగా గీచిన రేఖాఖండం ఒకటి.
కావున ఏర్పడే త్రిభుజాలు 1 + 2 = 3
∴ మొత్తం త్రిభుజాలు 6 + 3 = 9

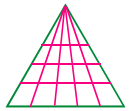
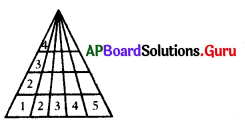
ప్రశ్న 2.

(a) 60
(b) 65
(c) 84
(d 90
సాధన.
(a) 60

వివరణ:
అడ్డువరుసల సంఖ్య = 4
ప్రతీ అడ్డువరుసలోని త్రిభుజాల సంఖ్య = 1 + 2 + 3 + 4 + 5 = 15
∴ మొత్తం. త్రిభుజాల సంఖ్య = 4 × 15 = 60

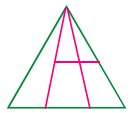
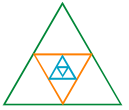
ప్రశ్న 3.

(a) 12
(b) 13
(c) 14
(d) 15
సాధన.
(b) 13

వివరణ: త్రిభుజాల సంఖ్య = 4n + 1, n = 3
= 4(3) + 1 = 12 + 1 = 13
(ఇక్కడ n. బయటి త్రిభుజంలో పొందుపరచబడిన త్రిభుజాల సంఖ్య)

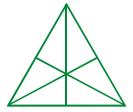
ప్రశ్న 4.

(a) 16
(b) 13
(c) 9
(d) 7
సాధన.
(a) 16

వివరణ:
బయటి త్రిభుజంలోని చిన్న త్రిభుజాలు = 6
3 శీర్షాల నుండి ఎదుటి భుజానికి గీచిన రేఖాఖండంతో ఏర్పడే త్రిభుజాలు = 3 × 2 = 6
ప్రతి భుజంపైన పై 3 రేఖాఖండాల ఖండన బిందువుతో ఏర్పడే త్రిభుజాలు = 3 × 1 = 3
వెలుపలి త్రిభుజము = 1
∴ మొత్తం త్రిభుజాలు = 6 + 6 + 3 + 1 = 16

ప్రశ్న 5.

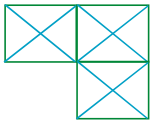
(a) 21
(b) 23
(c) 25
(d) 29
సాధన.
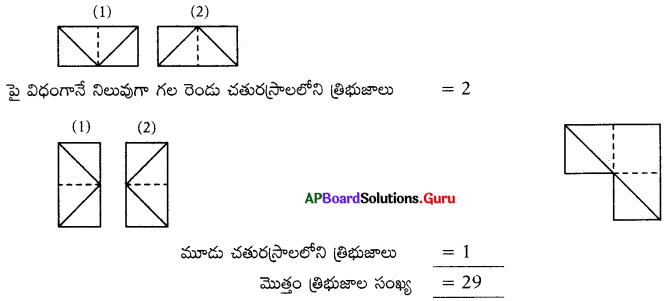
(d) 29.

వివరణ:
3 చతురస్రాలు కలవు, ప్రతి చతురస్రంలోని కర్ణాలు = 2
ప్రతి చతురస్రంలోని భాగాల సంఖ్య = 4
ఒక్కొక్క చతురస్రంలోని త్రిభుజాల సంఖ్య = 2 × 4 = 8
∴ 3 చతురస్రాలలోని త్రిభుజాలు = 3 × 8
అడ్డంగా గల రెండు చతురస్రాలలో ఏర్పడే త్రిభుజాలు = 2

ప్రశ్న 6.

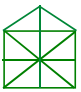
(a) 10
(b) 19
(c) 21
(d) 23
సాధన.
(c) 21

వివరణ:

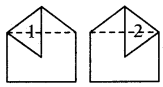
చతుర్భుజంలోని కర్ణాలు = 2
చతుర్భుజంలోని భాగాలు = 8
మొత్తం త్రిభుజాలు = 2 × 8
పైనున్న త్రిభుజంలోని త్రిభుజాలు = 1 + 2
చతురస్రము, పైనున్న త్రిభుజంలో ఏర్పడే త్రిభుజాలు
మొత్తం త్రిభుజాల సంఖ్య

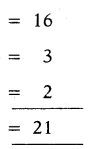
ప్రశ్న 7.

(a) 5
(b) 6
(c) 8
(d) 10
సాధన.
(c) 8

వివరణ:
బయట ఉన్న చిన్న త్రిభుజాలు = 5
మూడు రేఖాఖండాలపై ఏర్పడే త్రిభుజాలు = 3
మొత్తం

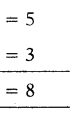
ప్రశ్న 8.

(a) 9
(b) 10
(c) 11
(d) 12
సాధన.
(a) 9

వివరణ: చతురస్రంలోని కర్ణాలు = 2, విభాగాలు = 4
చతురస్రంలోని త్రిభుజాలు = 4 × 2 = 8
చతురస్రం పైన త్రిభుజాలు = 1

మొత్తం

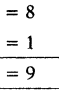
ప్రశ్న 9.

(a) 19
(b) 20
(c) 16
(d) 14
సాధన.
(a) 19

వివరణ:

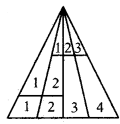
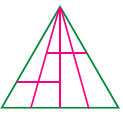
శీర్షం నుండి ఎదుటి భుజానికి గీచిన 3 రేఖాఖండాలతో ఏర్పడే భాగాలు 4.
కావున ఏర్పడే త్రిభుజాలు = 1 + 2 + 3 + 4
క్రింది భాగంలోని అడ్డు రేఖతో ఏర్పడే భాగాలు 2, కావున ఏర్పడే త్రిభుజాలు = 1 + 2 = 3
పై అడ్డు రేఖతో ఏర్పడే త్రిభుజాలు = 1 + 2 + 3
మొత్తం

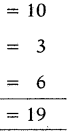
ప్రశ్న 10.

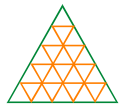
(a) 56
(b) 48
(c) 32
(d) 60
సాధన.
(b) 48

వివరణ:
మొత్తం త్రిభుజాల సంఖ్య = \(\frac{n(n+2)(2 n+1)}{8}\) లోని పూర్ణాంక భాగం.
[ఇక్కడ 1, త్రిభుజ భుజంపై గల త్రిభుజాల సంఖ్య. ∴ n = 5]
= \(\frac{5(5+2)(10+1)}{8}\)
= \(\frac{5 \times 7 \times 11}{8}\) = \(\frac{385}{2}\)
= 48.125 లో పూర్ణాంక భాగం = 48.
∴ మొత్తం త్రిభుజాల సంఖ్య = 48.