AP Board 7th Class Maths Solutions Chapter 10 Algebraic Expressions Ex 3

AP State Syllabus AP Board 7th Class Maths Solutions Chapter 10 Algebraic Expressions Ex 3 Textbook Questions and Answers.

AP State Syllabus 7th Class Maths Solutions 10th Lesson Algebraic Expressions Exercise 3

Question 1.
Find the length of the line segment PR in the following figure in terms of ’a’.

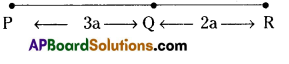
Solution:
The length of PR = \(\overline{\mathrm{PQ}}+\overline{\mathrm{QR}}\)
= 3a + 2a
= 5a units

Question 2.
(i) Find the perimeter of the following triangle.

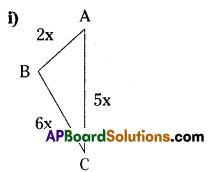
(ii) Find the perimeter of the following rectangle.

Solution:
i) The perimeter of the triangle = \(\overline{\mathrm{AB}}+\overline{\mathrm{BC}}+\overline{\mathrm{CA}}\)
= 2x + 6x + 5x
= 13x units
ii) The perimeter of the rectangle ABCD = \(\overline{\mathrm{AB}}+\overline{\mathrm{BC}}+\overline{\mathrm{CD}}+\overline{\mathrm{DA}}\)
or
= 2 (l + b)
= 2 (3x + 2x)
= 2 × 5x
= 10x units

Question 3.
Subtract the second terni from first term.
(i) 8x, 5x
(ii) 5p, 11p
(iii) 13m², 2m²
Solution:
i) 8x – 5x = 3x
ii) 5p – 11p = -6p
iii) 13m² – 2m² = 11m²

Question 4.
Find the value of following monomials, if x =1.
(i) -x
(ii) 4x
(iii) -2x²
Solution:
1) If x = 1 ⇒ – x = – (1)= – 1
ii) If x = 1 ⇒ 4x = 4 x 1 = 4
iii) If x= 1 ⇒ – 2x² = – 2(1)² = – 2 × 1= – 2

Question 5.
Simplify and find the value of 4x + x – 2x² + x – 1 when x = -1.
Solution:
Given expression = 4x + x – 2x² + x – 1
= 4x + x + x – 2x² – 1
= – 2x² + 6x – 1
If x = – 1 then, the value of – 2x² + 6x – 1 = – 2 (-1)2 + 6( – 1) – 1
= – 2(1) – 6 – 1
= – 2 – 6 – 1
= – 9

Question 6.
Write the expression 5x² – 4 – 3x² + 6x + 8 + 5x – 13 in its simplified form. Find its value when x = -2
Solution:
The given algebraic expression = 5x² – 4 – 3x² + 6x + 8 + 5x – 13.
= (5x² – 3x²) (6x + 5x) + (-4 – 13)
= 2x² + 11x – 17
When x = – 2. then the value of 2x²+ 11x – 17 = 2(- 2)² + 11(-2) – 17
= 2 × 4 – 22 – 17
= 8 – 39
= – 31

Question 7.
If x = 1; y = 2 find the values of the following expressions
(i) 4x – 3y + 5
(ii) x² + y²
(iii) xy + 3y – 9
Solution:
i) 4x – 3y+5
If x = 1, y = 2 then the value of 4x – 3y + 5 = 4(1) – 3(2) + 5
= 4 – 6 + 5
= 9 – 6 = 3

ii) x² + y²
If x = 1, y = 2, the value of x² + y²= (1)² + (2)²
=(1 × 1) + (2 × 2)
= 5

iii) xy + 3y – 9
If x = 1; y = 2,the value of xy + 3y – 9 = 1 × 2 + 3(2) – 9
= 2 + 6 – 9
= 8 – 9

Question 8.
Area of a rectangle is given by A = l × b . If l = 9cm, b = 6cm, find its area?
Solution:
Formula for area of a rectangle (A) = l × b
If l = 9cm, b = 6cm
then the area of the rectangle = l × b
= 9 × 6
= 54 cm²

Question 9.
Simple interest is given by I = \(\frac{P T R}{100}\) . If P = ₹ 900, T =2 years; and R =5%, find the simple interest.
Solution:
Given that the formula for simple interest (I) = \(\frac{P T R}{100}\)
P = Rs.900, T = 2years, R = 5%
∴ The required simple interest (I) = \(\frac{\mathrm{PTR}}{100}=\frac{900 \times 2 \times 5}{100}\) = 9 x 2 x 5 = Rs. 90

Question 10.
The relationship between speed (s), distance (d) and time (t) is given by S = – . Find the
value of s, if d = 135 meters and t = 10 seconds.
Solution:
Given that s = \(\frac{\mathrm{d}}{\mathrm{t}}\) and d = 135 meters, t = 10 seconds
∴ The value of s = \(\frac{\mathrm{d}}{\mathrm{t}}=\frac{135}{10}\)
∴ speed (s) = 13.5 m/sec.