AP State Syllabus AP Board 7th Class Maths Solutions Chapter 1 Integers InText Questions and Answers.
AP State Syllabus 7th Class Maths Solutions 1st Lesson Integers InText Questions
![]()
Try This
Question 1. (Page No. 3)
9 + (-3) =
9 + (- 2) =
9 + C- 1) =
9 + 0 =
9 + 1 =
9 + 2 =
9 + 3 =
9 + 4 =
9 + 5 =
9 + 6 = 15
9 + 7 = 16
Solution:
9 + (- 3) = 6
9 + (- 2) = 7
9 + (- 1) = 8
9 + 0 =9
9 + 1 =10
9 + 2 = 11
9 + 3= 12
9 + 4 = 13
9 + 5 = 14
9 + 6 = 15
9 + 7 = 16
![]()
i) When you added a positive integer, in which direction did you move on the number line ? (Page No. 4)
Solution:
When you add a positive integer you move right side on the number line.
ii) When you added a negative integer in which direction did you move on the number line ? (Page No. 4)
Solution:
When you add a negative integer you move left side on the number line.
Question 2.
Sangeetha said that each time you add two integers, the value of the sum is greater than the numbers. Is Sangeetha right ? Give reasons for your answer. (Page No. 4)
Solution:
Sangeetha is always not correct. When we add – 8 and 3 the sum is (- 8) + 3 = – 5 which is less than 3. Therefore when we add two positive integers then only the sum is greater than the numbers.
Try This
Complete the pattern. (Page No. 5)
Question 1.
8-6 = 2
8-5 = 3
8-4 =
8-3 =
8-2 =
8-1 =
8 – 0 =
8 – (- 1) =
8 – (- 2) =
8 – (- 3) =
8 – (- 4) =
Solution:
8-6 = 2
8-5 = 3
8-4 = 4
8-3 = 5
8-2 = 6
8-1 = 7
8-0 =8
8 – (- 1) =9
8 – (-2) =10
8 – (- 3) = 11
8 – (-4) =12
![]()
i) When you subtract a positive integer in which direction do you move on the number line ? (Page No. 5)
Solution:
When you subtract a positive integer, you move left side on the number line.
ii) When you subtract a negative integer, in which direction do you move on the number line ? (Page No. 5)
Solution:
When you subtract a negative integer, you move right side on the number line.
Question 2.
Richa felt that each time you subtract an integer from another integer, the value of the difference is lesser than the two numbers. Is Richa right ? Give reasons for your answer. (Page No. 5)
Solution:
Richa may not be correct all times. Richa is correct when we subtract a positive integer, but when we subtract a negative integer the difference is greater than the two numbers.
E.g: 8 – (- 3) = 11 11 > 8 and 11 > – 3
5-(-6) = 11 11 > 5 and 11 >-6
7-(-8) = 15 15 > 7 and 15 > – 8
Do this
Question 1.
Solve the following. (Page No. 7)
i) 2 x – 6 =
Solution:
i) 2 x -6 = -12
ii) 5 x – 4 =
Solution:
ii) 5 x – 4 = – 20
iii) 9 x – 4 =
Solution:
iii) 9 x – 4 = – 36
![]()
Activity
Question
Fill the grid by multiplying each number in the first column with each number in the first row. (Page No. 9)
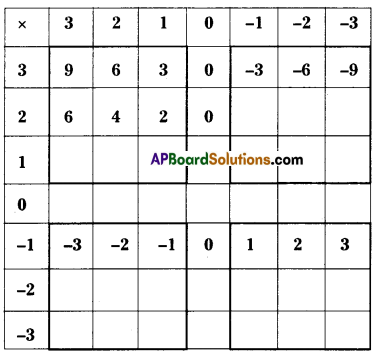
i) Is the product of two positive integers always a positive integer ?
ii) Is the product of two negative integers always a positive integer ?
iii) Is the product of a negative and positive integer always a negative integer ?
Solution:
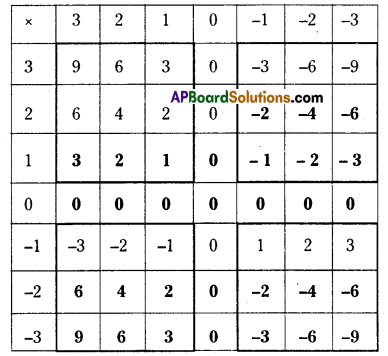
i) Yes
ii) Yes
iii) Yes
Try This
(Page No. 10)
a) (- 1) x (- 1) =
b) (- 1) x (- 1) x (- 1) =
c) (- 1) x (- 1) x (- 1) x (- 1) =
d) (- 1) x (- 1) x (- 1) x (- 1) x (- 1) =
Solution
a) (- 1) x (- 1) = 1
b) (- 1) x (- 1) x (- 1) = – 1
c) (- 1) x (- 1) x (- 1) x (- 1) = 1
d) (- 1) x (- 1) x (- 1) x (- 1) x (- 1) = – 1
![]()
Do This
Solve the following. (Page No. 12)
i) (- 100) ÷ 5 =
Solution:
-20
ii) (-81)-9 =
Solution:
-9
iii)(- 75) – 5 =
Solution:
– 15
iv) (- 32) – 2 =
Solution:
– 16
v) 125-(-25) =
Solution:
– 5
vi) 80-(-5) =
Solution:
– 16
vii) 64 ÷ (-16)
Solution:
-4
Do This
Question 2.
Compute the following. (Page No. 13)
i) -36 ÷ (-4) =
Solution:
9
ii) (-201) ÷ (-3) =
Solution:
67
iii) (-325) ÷ (- 13)=
Solution:
25
![]()
Try This
Question 1.
Can we say that (- 48) + 8 = 48 + (- 8) ? (Page No. 12)
Solution:
Yes.
Check whether
i) 90 ÷ (- 45) and (- 90) ÷ (45)
Solution:
90 ÷ – 45 = – 2 and – 90 45 = – 2
∴ 90 ÷ (-45) = -90 ÷ 45 .
ii) (- 136) ÷ 4 and 136 ÷ (- 4)
Solution:
(- 136) ÷ 4 = – 34 and 136 ÷ (- 4) = – 34
∴ (- 136) ÷ 4 = (136) ÷ (-4)
Question 2.
i) (2 + 5) + 4 = 2 + (5 + 4)
ii) (2 + 0) + 4 = 2 + (0 + 4) (Page No. 15)
Does the associative property hold for whole numbers ? Take two more examples and write your answer.
Solution:
Yes. The associative property holds for whole numbers.
Ex : i) 5 + (6 + 8) = (5 + 6) + 8
ii) 3 + (5 + 4) = (3 + 5) + 4
![]()
Question 3.
Add the following. (Page No. 15)
i) 2 + 0
ii) 0 + 3 =
iii) 5 + 0 =
Solution:
i) 2
ii) 3
iii) 5
Question 4.
Similarly, add zero to as many whole numbers as possible. Is zero the additive identity for whole numbers ? (Page No. 15)
Solution:
4+0=4
8+0=8
0+7=7
1+0=1
Therefore zero is the additive identity for whole numbers.
Question 5.
Multiply the following. (Page No. 15)
i) 2 x 3 = …………..
ii) 5 x 4 = …………..
iii) 3 x 6 = …………..
Solution:
i) 6
ii) 20
iii) 18
![]()
Question 6.
Similarly, multiply any two whole numbers of your choice. (Page No. 17)
Is the product of two whole numbers always a whole number ?
Solutlion:
3 x 5 = 15
8 x 2 = 16
4 x 3 = 12
Yes, the product of two whole number is always a whole number.
Question 7.
(5 x 2) x 3 = 5 x (2 x 3) (Page No. 18)
Is the associative property true for whole number. Take many more examples and verify.
i) 4 x (3 x 2) = (4 x 3) x 2
4 x 6 = 12 x 2
24 = 24
ii) (8 x 5) x 2 = 8 x (5 x 2)
40 x 2 = 8 x 10
80 = 80
iii) (3 x 6) x 5 = 3 x (6 x 5)
18 x 5 = 3 x 30
90 = 90
Do This
Question 1.
Compute the following : (Page No. 13)
i) -36 ÷ (-4) = \(\frac{-36}{-4}\) = 9
ii)(-201) ÷ (-3) = \(\frac{-201}{-3}=\frac{201}{3}\) = 67
iii) (-325) ÷ (-13) = \(\frac{-325}{-13}\) = 25
Question 2.
Is [(- 5) x 2] x 3 = (- 5) x [(2 x 3)] ? (Page No. 18)
Solution:
LHS : [- 10] x 3 = – 30
RHS : (- 5) x (6) =-30
∴ L.H.S = R.H.S
![]()
Question 3.
Is [(- 2) x 6] x 4 = (- 2) x [(6 x 4)] ? (Page No. 18)
Solution:
LHS: [-12] x 4 = -48
RHS : (-2) x (24) =-48.
∴ L.H.S = R.H.S
Try This
Question 1.
Take at least 5 different pairs of Integers and see if subtraction is commutative.
i) Consider 5 and -3 (Page No. 20)
5 – ( – 3) = 5 + 3 = 8
(-3) – 5 = -8
Therefore 5 – (-3) ≠ (-3) – 5
ii) Consider 7 and -5
7-(-5) = 7 + 5 = 12
(-5) – 7 = -12
Therefore 7 – (-5) ≠ (- 5) – 7
iii) Consider 2 and – 6
2 – (-6) = 2 + 6 = 8
(-6)- 2 = -8
Therefore 2 – (-6) ≠ (- 6) – 2
![]()
iv) Consider -4 and 5
(- 4) – (5) = -9
5- (-4) = 5 + 4 = 9
∴ (-4) – 5 ≠ 5 – (-4)
v) -3 and 8
(-3)- 8 = – 11
8 – (-3) = 8 + 3 = 11
∴(-3)-8 ≠ 8-(-3)
Hence subtraction ¡s not commutative over integers.
Question 2.
Take at least five pairs of integers and check whether they are closed under division. (Page No. 21)
Statement — Inference
i) 12 +- (- 2) = – 6 — Result is an integer
Try This
Question 1.
Show 8 – 6, 8 – 1, 8 – 0, 8 – ( -2), 8 – ( – 4) on the number line. (Page No. 5)
Solution:

∴ 8 – 6 = 2; 8 – 1 = 7; 8 – 0 = 8; 8 – (-2) = 10; 8 – (-4) = 12