AP State Syllabus AP Board 6th Class Maths Solutions Chapter 6 Basic Arithmetic Ex 6.1 Textbook Questions and Answers.
AP State Syllabus 6th Class Maths Solutions 6th Lesson Basic Arithmetic Ex 6.1
Question 1.
Express the following in the terms of ratios.
i) The length of a rectangle is 5 times to its breadth.
ii) For preparing coffee, 2 cups of water require to 1 cup of milk.
Answer:
i) Let the breadth of rectangle = x = 1 part
length of rectangle = 5x = 5 parts
Ratio = length : breadth = 5x : x = \(\frac{5x}{x}\) = \(\frac{5}{1}\) = 5 : 1
ii) To prepare coffee,
Required cups of water = 2
Required cups of milk = 1
Ratio = water : milk = 2 : 1
![]()
Question 2.
Express the following in the simplest form.
i) 24 : 9
ii) 144 : 12
iii) 961 : 31
iv) 1575 : 1190
Answer:
i) 24 : 9
Given ratio is 24 : 9
To write the given ratio in the simplest form.
First find the HCF of two terms.
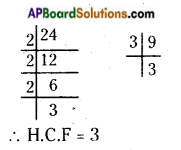
HCF of 24 and 9 is 3.
Then, divide each term by their HCF.
Simplest form of the ratio = 24 ÷ 3 : 9 ÷ 3
Required ratio = 8 : 3
ii) 144 : 12
Given ratio is 144 : 12
To write the given ratio in the simplest form.
First find the HCF of two terms.
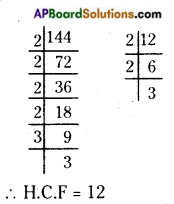
HCF of 144 and 12 is 12.
Then, divide each term by their HCF.
Simplest form of the ratio = 144 ÷ 12 : 12 ÷ 12
Required ratio = 12 : 1
![]()
iii) 961 : 31
Given ratio is 961 : 31
To write the given ratio in the simplest form.
First find the HCF of two terms.
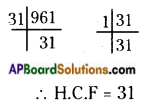
HCF of 961 and 31 is 31.
Then, divide each term by their HCF.
Simplest form of the ratio = 961 ÷ 31 : 31 ÷ 31
Required ratio = 31 : 1
iv) 1575 : 1190
Given ratio is 1575 : 1190
To write the given ratio in the simplest form.
First find the HCF of two terms.
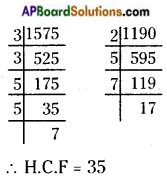
HCF of 1575 and 1190 is 35.
Then, divide each term by their HCF.
Simplest form of the ratio = 1575 ÷ 35 : 1190 ÷ 35
∴ Required ratio = 45 : 34
Question 3.
Write the antecedents and consequents of the following ratios.
(i) 36 : 73
(ii) 65 : 84
(iii) 58 : 97
(iv) 69 : 137
Answer:
| S.No. | Ratio | Antecedents | Consequents |
| (i) | 36: 73 | 36 | 73 |
| (ii) | 65 : 84 | 65 | 84 |
| (iii) | 58:97 | 58 | 97 |
| (iv) | 69 : 137 | 69 | 137 |
![]()
Question 4.
Find the ratios of the following in their simplest form.
i) 25 minutes to 55 minutes
ii) 45 seconds to 30 minutes
iii) 4 m 20 cm to 8 m 40 cm
iv) 5 litres to 0.75 litres
v) 4 weeks to 4 days
vi) 5 dozen to 2 scores (1 score = 20 items)
Answer:
i) 25 minutes to 55 minutes
Given 25 minutes to 55 minutes = 25 : 55

HCF of 25 and 55 is 5 = 25 ÷ 5 : 55 ÷ 5 (Divide each term by 5)
∴ Required ratio = 5:11
ii) 45 seconds to 30 minutes
Given 45 seconds to 30 minutes.
To write the given ratio in the simplest form.
First convert the two terms into same units.
1 minute = 60 seconds
30 minutes = 30 × 60 = 1800 seconds
Then, find the HCF of two terms and divide them by their HCF.
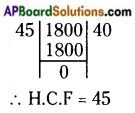
HCF of 45 and 1800 is 45.
= 45 ÷ 45 : 1800 ÷ 45 (divide each term by 45)
∴ Required ratio = 1 : 40
![]()
iii) 4 m 20 cm to 8 m 40 cm
Given 4 m 20 cm to 8 m 40 cm
To write the given ratio in the simplest form.
First we convert them into cm.
1 m = 100 cm
4 m = 400 cm
8 m = 800 cm
4 m 20 cm = 400 + 20 = 420 cm
8 m 40 cm = 800 + 40 = 840 cm
Then, find the HCF of 420 and 840 and divide them by HCF.
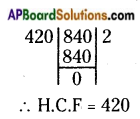
HCF of 420 and 840 is 420.
= 420 ÷ 420 : 840 ÷ 420 (divide each term by 420)
Required ratio = 1 : 2.
iv) 5 litres to 0.75 litres
Given 5 litres to 0.75 litres
To write the given ratio in the simplest form, first we convert litres into millilitres.
1 litre = 1000 ml
5 litres = 5000 ml
0.75 litres = 750 ml
Then, find the HCF of 5000; 750 and divide them by HCF.
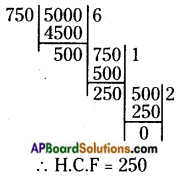
HCF of 5000 and 750 is 250,
= 5000 ÷ 250 : 750 ÷ 250 (divide each term by 250)
Required ratio = 20 : 3
![]()
v) 4 weeks to 4 days
Given 4 weeks to 4 days.
To write the given ratio in the simplest form, first we convert them into same units (days).
1 week = 7 days
4 weeks = 4 × 7 = 28 days
Then, find the HCF of 28 and 4, then divide them by HCF.
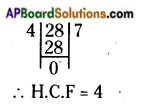
HCF of 28 and 4 is 4 = 28 ÷ 4 : 4 ÷ 4 (divide each term by 4)
Required ratio = 7 : 1
vi) 5 dozen to 2 scores (1 score = 20 items)
Given 5 dozen to 2 scores.
To write the given ratio in the simplest form, first we convert them into same units.
1 dozen = 12 items
5 dozens = 5 × 12 = 60 items
1 score = 20 items
2 scores = 2 × 20 = 40 items
Then, find the HCF of 60 and 40, divide them by HCF.

HCF of 60 and 40 is 20 = 60 ÷ 20 : 40 ÷ 20 (divide each term by 20)
Required ratio = 3 : 2
![]()
Question 5.
Rahim works in a software company and earns Rs. 75,000/- per month. He saves Rs. 28,000/- per month from his earnings. Find the ratio of
i) His savings to his income
ii) His income to his expenditure
iii) His savings to his expenditure
Answer:
Given Rahim’s monthly income = Rs. 75000
monthly savings = Rs. 28000
Monthly expenditure = income – savings
= 75000 – 28000 = 47,000/-
i) Ratio of savings to income = 28000 : 75000
To convert the ratio into the simplest form divide each term by their HCF is 1000
= 28000 ÷ 1000 : 75000 ÷ 1000 (divide by 1000)
= 28 : 75
Required ratio of savings to income = 28 : 75
ii) Ratio of income to expenditure = 75000 : 47000
To convert the ratio into the simplest form divide each term by their HCF is 1000 = 75000 ÷ 1000 : 47000 ÷ 1000 (divide by 1000)
= 75 : 47
Required ratio of income to expenditure = 75 : 47
iii) Ratio of savings to expenditure = 28000 : 47000
To convert the ratio into the simplest form divide each term by their HCF is 1000 = 28000 ÷ 1000 : 47000 ÷ 1000 (divide by 1000)
= 28 : 47
Required ratio of savings to expenditure = 28 : 47