AP State Syllabus AP Board 6th Class Maths Solutions Chapter 5 Fractions and Decimals Ex 5.1 Textbook Questions and Answers.
AP State Syllabus 6th Class Maths Solutions 5th Lesson Fractions and Decimals Ex 5.1
Question 1.
Classify the fractions as proper, improper and mixed.
\(\frac{3}{4}\), \(\frac{6}{5}\), \(\frac{3}{2}\),\(\frac{4}{1}\), \(\frac{2}{3}\), \(\frac{1}{4}\), \(\frac{18}{13}\), 1\(\frac{5}{7}\),\(\frac{1}{3}\), 11\(\frac{1}{2}\)
Answer:
If in a fraction numerator is less than the denominator, then it is called a proper fraction.
Proper fractions are \(\frac{3}{4}\), \(\frac{2}{3}\), \(\frac{1}{4}\), \(\frac{1}{3}\)
If in a fraction numerator is greater than the denominator, then it is called an improper fraction.
Improper fractions are \(\frac{6}{5}\), \(\frac{3}{2}\), \(\frac{4}{1}\), \(\frac{18}{13}\)
A combination of a whole number and a proper fraction is called a mixed fraction.
Mixed fractions are 1\(\frac{5}{7}\), 11\(\frac{1}{2}\)
![]()
Question 2.
Write the following fractions in an ascending order.
i) \(\frac{3}{4}\), \(\frac{3}{2}\), \(\frac{2}{3}\), \(\frac{1}{5}\), \(\frac{18}{7}\)
ii) \(\frac{2}{7}\), \(\frac{3}{8}\), \(\frac{3}{4}\), \(\frac{5}{7}\), \(\frac{4}{9}\)
Answer:
Given fractions are \(\frac{3}{4}\), \(\frac{3}{2}\), \(\frac{2}{3}\), \(\frac{1}{5}\), \(\frac{18}{7}\)
These are unlike fractions.
To arrange the unlike fractions in ascending order / descending order first we have to convert them into equivalent fractions with LCM of their denominators, then compare the like fractions (i.e.,) we convert them to like fractions.
LCM of Denominators = 2 × 2 × 3 × 5 × 7 = 420

\(\frac{315}{420}\), \(\frac{630}{420}\), \(\frac{280}{420}\), \(\frac{84}{420}\), \(\frac{1080}{420}\)
These are like fractions. Now, we can compare them.
\(\frac{84}{420}\)< \(\frac{280}{420}\) < \(\frac{315}{420}\) < \(\frac{630}{420}\) < \(\frac{1080}{420}\)
i.e, \(\frac{1}{5}\) < \(\frac{2}{3}\) < \(\frac{3}{4}\) < \(\frac{3}{2}\) < \(\frac{18}{7}\)
∴ Ascending order: \(\frac{1}{5}\), \(\frac{2}{3}\), \(\frac{3}{4}\), \(\frac{3}{2}\), \(\frac{18}{7}\)
Descending order: \(\frac{18}{7}\), \(\frac{3}{2}\), \(\frac{3}{4}\), \(\frac{2}{3}\), \(\frac{1}{5}\)
![]()
ii) \(\frac{2}{7}\), \(\frac{3}{8}\), \(\frac{3}{4}\), \(\frac{5}{7}\), \(\frac{4}{9}\)
These are unlike fractions.
To arrange the unlike fractions in ascending order / descending order first we have to convert them into equivalent fractions with LCM of their denominators. Then compare the like fractions (i.e.,) we convert them to like fractions.
LCM of denominators = 2 × 2 × 2 × 3 × 3 × 7 = 504

\(\frac{144}{504}\), \(\frac{189}{504}\), \(\frac{378}{504}\), \(\frac{360}{504}\), \(\frac{224}{504}\)
These are like fractions. Now, we can compare them.
\(\frac{144}{504}\) < \(\frac{189}{504}\) < \(\frac{224}{504}\) < \(\frac{360}{504}\) < \(\frac{1080}{420}\)
i.e, \(\frac{2}{7}\) < \(\frac{3}{8}\) < \(\frac{4}{9}\) < \(\frac{5}{7}\) < \(\frac{3}{4}\)
∴ Ascending order: \(\frac{2}{7}\), \(\frac{3}{8}\), \(\frac{4}{9}\), \(\frac{5}{7}\), \(\frac{3}{4}\)
Descending order: \(\frac{3}{4}\), \(\frac{5}{7}\), \(\frac{4}{9}\), \(\frac{3}{8}\), \(\frac{2}{7}\)
![]()
Question 3.
Without doing calculation, find the result \(\frac{2}{3}\) + 1\(\frac{3}{4}\) + \(\frac{1}{3}\) – \(\frac{1}{4}\)
Answer:
Given \(\frac{2}{3}\) + 1\(\frac{3}{4}\) + \(\frac{1}{3}\) – \(\frac{1}{4}\)

Question 4.
Neha bought a cake. She ate \(\frac{7}{15}\) th of the cake immediately add in the afternoon she ate the remaining part. How much part die ate in the afternoon ?
Answer:
Whole cake = 1 = \(\frac{15}{15}\)
Neha divided the cake into 15 parts.
Part of a cake eaten by Neha = \(\frac{7}{15}\)
Remaining part of cake = Whole – eaten part immediately
= \(\frac{1}{1}\) – \(\frac{7}{15}\)
= \(\frac{15}{15}\) – \(\frac{7}{15}\)
= \(\frac{15-7}{15}\)
= \(\frac{8}{15}\)
∴ Part of a cake eaten by Neha in the afternoon = \(\frac{8}{15}\)
![]()
Question 5.
Simplify:
i) \(\frac{2}{5}\) + \(\frac{1}{3}\)
ii) \(\frac{5}{7}\) + \(\frac{2}{3}\)
iii) \(\frac{3}{5}\) – \(\frac{7}{20}\)
iv) \(\frac{17}{20}\) – \(\frac{13}{25}\)
Answer:
i) \(\frac{2}{5}\) + \(\frac{1}{3}\)
LCM of denominators = 3 × 5 = 15

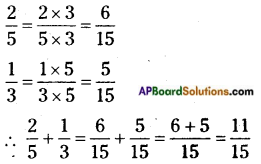
ii) \(\frac{5}{7}\) + \(\frac{2}{3}\)
LCM of denominators = 7 × 3 = 21


iii) \(\frac{3}{5}\) – \(\frac{7}{20}\)
LCM of denominators = 2 × 2 × 5 = 20


iv) \(\frac{17}{20}\) – \(\frac{13}{25}\)
LCM of denominators = 2 × 2 × 5 × 5 = 100

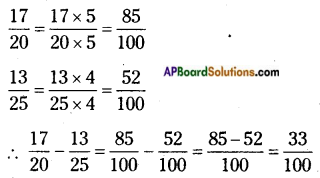
![]()
Question 6.
Represent \(\frac{16}{5}\) pictorially
Answer:
Given fraction is \(\frac{16}{5}\) (Improper fraction)
\(\frac{16}{5}\) = Mixed fraction is 3\(\frac{1}{5}\)

3 + \(\frac{1}{5}\) = 3\(\frac{1}{5}\)