AP State Syllabus AP Board 6th Class Maths Solutions Chapter 11 Perimeter and Area Ex 11.2 Textbook Questions and Answers.
AP State Syllabus 6th Class Maths Solutions 11th Lesson Perimeter and Area Ex 11.2
![]()
Question 1.
Find the circumferences of the circles with the radius given below.
A) 7 cm B) 3.5 cm C) 14 cm
Solution:
A) Given radius (r) = 7 cm
Circumference of a circle C = 2πr (∵ π = \(\frac{22}{7}\))
= 2 x \(\frac{22}{7}\) x 7 = 44 cm
∴ Circumference of a circle = 44 cm ‘
B) Given radius (r) = 3.5 cm
Circumference of a circle C = 2πr (∵ π = \(\frac{22}{7}\))
= 2 x \(\frac{22}{7}\) x 3.5
∴ Circumference of a circle = 22 cm
C) Given radius (r) = 14 cm
Circumference of a circle C = 2πr (∵ π = \(\frac{22}{7}\))
= 2 x \(\frac{22}{7}\) x 14
∴ Circumference of a circle = 88 cm
![]()
Question 2.
Given below are the circumferences of different circles. Find the radius of each circle.
A) 4.4 m B) 176 cm C) 1.54 cm
Solution:
A) Given circumference of a circle = 2πr = 4.4 m
2 x \(\frac{22}{7}\) x r = 4.4
Divide with 2 x \(\frac{22}{7}\) on both sides.
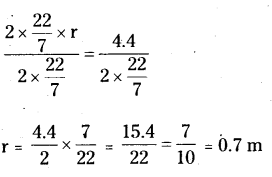
∴ Radius of the circle (r) = 0.7 m = 70 cm.
B) Given circumference of a circle = 2πr =176 cm
2 x \(\frac{22}{7}\) x r = 176
Divide with 2 x \(\frac{22}{7}\) on both sides.

∴ Radius of the circle (r) = 28 cm.
C) Given circumference of a circle is C = 2πr = 1.54 cm
2 x \(\frac{22}{7}\) x r = 1.54
Divide with 2 x \(\frac{22}{7}\) on both sides.

∴ Radius of the circle (r) = 0.245 cm
Question 3.
A gold smith has 8.8m of gold wire with him. He has to make gold rings of 2cm radius. How many such rings he can make with it?
Solution:
Given the radius of the gold ring r = 2 cm
Length of the gold wire = 8.8 m (or) = 880 cm
To find the? number of rings we have to divide the length of the gold wire by circumference of the gold ring.
Now, circumference of the gold ring C = 2πr
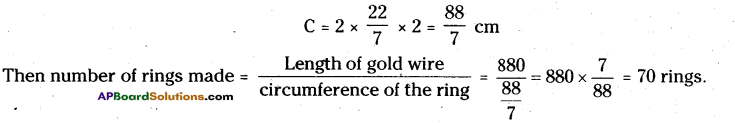
Number of rings made by gold smith = 70
![]()
Question 4.
A wire was bent in the shape of a circle with radius 7cm. If the same wire was again used to make a square, then find its side.
Solution:
Given radius of the circle r = 7 cm
Circumference of the circle C = 2πr
= 2 x \(\frac{22}{7}\) x 7 = 44 cm
Given length of the wire same.
So, perimeter of square = circumference of the circle
4 x side = 44 cm
Divide with 4 on both sides = \(\frac{4 \times \text { side }}{4}=\frac{44}{4}\)
Side = 11 cm
∴ Side of square = 11cm.
Question 5.
In a chemical factory two wheels of different radius were connected with a belt. Radius of the bigger wheel is 21cm and radius of the smaller wheel is 7cm. If the bigger wheel rotates completely 100 times, find out the number of times that the smaller wheel rotates. .
Solution:
Given the radius of the bigger wheel R = 21 cm
Circumference of the bigger wheel C = 2πR = 2 x \(\frac{22}{7}\) x 21 = 132 cm
If the bigger wheel completes 100 rotations,
Distance covered by the bigger wheel = Number of rotates x circumference
= 100 x 132 = 13,200 cm
Now, radius of smaller wheel r = 7 cm.
Circumference of the smaller wheel C = 2πr = 2 x \(\frac{22}{7}\) x 7 = 44cm
If the smaller wheel completes ‘n’ rotations,
Distance covered by the smaller wheel = number of rotations x circumference
= n x 44 = 44n cm
Distance covered by the small wheel = Distance covered by the bigger wheel
44n = 13200 cm
Divide with 44 as both sides,
\(\frac{44 n}{44}=\frac{13200}{44}\) = 300
n = 300
∴ Number of rotations made by the smaller wheel = 300.
Question 6.
Mohan is playing with a ring of diameter 14 cm, which is made up of metallic wire. When his brother asked, Mohan stretched the wire and made it as two equal parts. With those parts, he made another two small rings. Find the radius of smaller ring. Sol. Given the diameter of the bigger ring
Solution:
Given the diameter of the bigger ring = 14 cm
Radius of the bigger ring R = \(\frac{\text { diameter }}{2}\)
R = \(\frac{14}{2}\) = 7 cm
Length of the wire = Circumference of the bigger ring
= 2πR = 2 x \(\frac{22}{7}\) x 7 = 44 cm
If Mohan stretched the wire into’ halves.
Then the length of half of the wire = circumference of the bigger ring ÷ 2
= \(\frac{44}{2}\) = 22 cm
Circumference of the smaller ring = 2πr = 22
2 x \(\frac{22}{7}\) x r = 22
Divide with 2 x \(\frac{22}{7}\) on both sides

∴ Radius of the smaller ring = 3.5 cm
![]()
Question 7.
In designing an iron gril a black smith needed 70 rings with radius of 7cm each. Find how much length of the rod he required, if the wastage is 20 cm.
Solution:
Given radius of the ring r = 7 cm
Circumference of the ring C = 2πr = 2 x \(\frac{22}{7}\) x 7 = 44 cm
Length of rod required to make one ring = 44 cm
Length of rod required to make 70 rings = 44 x 70 = 3080 cm
Wastage = 20 cm
Required length of rod to make 70 rings = 3080 + 20 = 3100 c