AP State Syllabus AP Board 6th Class Maths Solutions Chapter 11 Perimeter and Area Ex 11.1 Textbook Questions and Answers.
AP State Syllabus 6th Class Maths Solutions 11th Lesson Perimeter and Area Ex 11.1
Question 1.
Find the perimeters of the following figures.
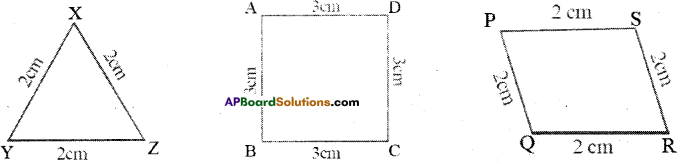
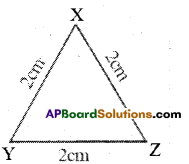
i) Check whether the perimeter of Δ XYZ = 3 x Length of the side?
ii) Check whether the perimeter of □ ABCD = 4 x Length of the side?
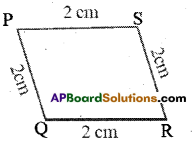
iii) Check whether the perimeter of □ PQRS = 4 x Length of the side?
i) In ΔXYZ, XY = 2cm, YZ = 2cm and XZ = 2cm
Perimeter of ΔXYZ = XY + YZ + XZ = 2 + 2 + 2 = 6cm
Perimeter of ΔXYZ = 6 cm
By observing that perimeter of ΔXYZ = 6cm = 3 x 2cm
= 3 x length of the side in ΔABC
So, perimeter of ΔXYZ = 3 x length of the side
ii) Given in quadrilateral ABCD, AB = 3cm, BC = 3cm, CD = 3cm and AD
Perimeter of □ ABCD = AB + BC + CD + AD = 3 + 3 + 3 + 3
Perimeter of □ ABCD = 12 cm
By observing that perimeter of □ ABCD = 12cm = 4 x 3cm
= 4 x length of the side in □ ABCD
So, perimeter of □ ABCD = 4 x length of the side
iii)In quadrilateral 
PQRS, .
Given PQ = 2cm, QR = 2cm, RS = 2cm and PS = 2cm
Perimeter of PQRS = PQ + QR + RS + PS = 2 + 2 + 2 + 2 = 8cm
Perimeter of PQRS = 8cm.
By observing that perimeter of PQRS = 8cm = 4×2 cm
= 4 x length of the side in PQRS
So, perimeter of PQRS = 4 x length of the side.
Question 2.
Measurements of two rectangular fields are 50m x 30m and 60m x 40m. Find their perimeters. Check whether the perimeters are 2 x length + 2 x breadth.
Solution:
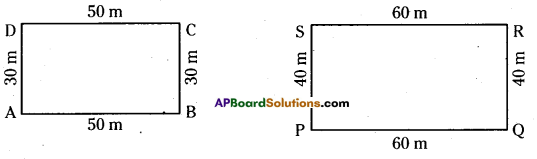
Given, in rectangle ABCD, AB = DC = 50 m and BC = DA = 30 m
Perimeter of rectangle ABCD = AB + BC + CD + DA
= 50 + 30 + 50 + 30
= 2 x 50 + 2x 30 = 160 m
∴ Perimeter of rectangle ABCD = 2 x length + 2 x breadth
Given in rectangle PQRS, PQ = RS = 60 m and QR = SP = 40 m
Perimeter of rectangle PQRS = PQ + QR + RS + SP
= 60 + 40 + 60 + 40
= 2 x 60 + 2 x 40 = 200 m
∴ Perimeter of rectangle PQRS = 2 x length + 2 x breadth
Question 3.
Find the perimeter of
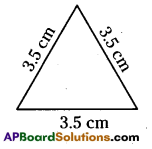
a) An equilateral triangle whose side is 3.5cm.
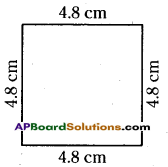
b) A square whose side is 4.8cm.
Solution:
a) Given side of an equilateral triangle is 3.5 cm.
We know that, perimeter of an equilateral triangle
= 3 x length of the side = 3 x 3.5 = 10.5 cm .
∴ Perimeter = 10.5 cm
b) Given side of a square = 4.8 cm
We know that, perimeter of a square
= 4 x length of the side 4 x 4.8
∴ Perimeter = 19.2 cm
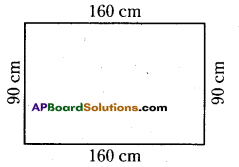
Question 4.
Length and breadth of top of one table is 160cm and 90cm respectively. Find how . much length of beading is required for each table.
Solution:
Given the length of top of table =160 cm
breadth of top of table = 90 cm g
To find the length of beading we have to find the ®
perimeter of the table top. .
So, perimeter of table top = 160 + 90 + 160 + 90 = 500 cm 160 cm
Required length of beading of table top = 500 cm.
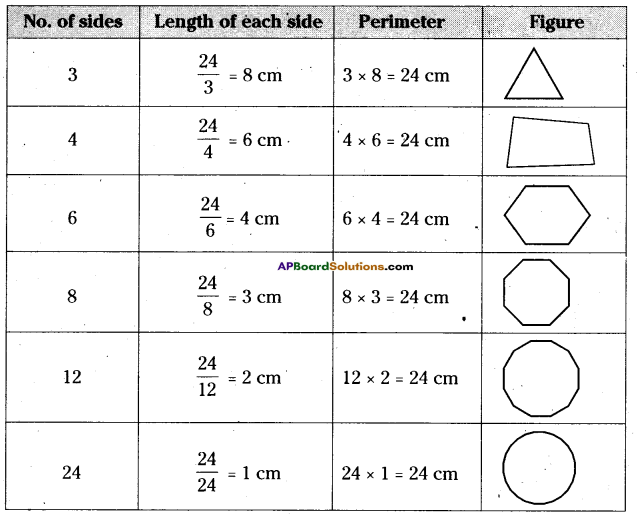
Question 5.
Manasa has 24cm of metallic wire with her. She wanted to make some polygons with equal sides whose sides are integral without milling into pieces values. Find how many such polygons she can make with the length of 24cm metallic wire?
Solution:
Given length of metallic wire = 24 cm
We know that 24 = 1 x 24
= 2 x 12
= 3 x 8
= 4 x 6
∴ 24 can be divided into 1,2,3,4,6,8,12 & 24
But we can’t form polygons with sides 1 & 2.
∴ The polygons with sides 3, 4, 6, 8, 12 and 24 can be formed.
The length of the sides are equal so \(\) and \(\) units.
They are 8 cm, 6cm, 4cm, 3cm, 2cm and 1cm respectively
Question 6.
Find the perimeter of the following figures. (i) and (ii)
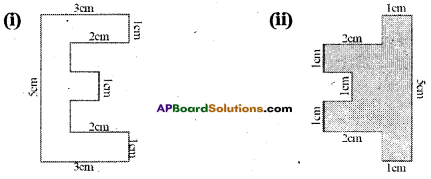
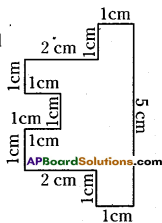
i) Perimeter of the given polygon is sum of the lengths of its all sides.
Perimeter = 5cm + 3cm+ 1cm + 2cm + 1 cm + 1 cm + 1 cm + 1 cm + 1cm + 2cm + 1 cm + 3cm
Perimeter = 22 cm
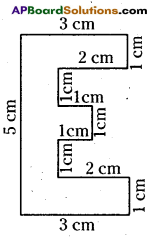
ii) Perimeter of the given polygon is sum of the lengths of its all sides.
Perimeter = 1cm + 5cm + 1 cm + lcm+ 2cm + 1cm + 1cm + 1cm + 1cm + 1cm + 2cm + 1cm
Perimeter = 18cm
Question 7.
Statement P : So many rectangles exists with the same perimeter.
Statement Q : So many squares exists with the same perimeter.
Which option is correct?
A) P wrong Q correct
B) P correct Q wrong
C) P and Q are correct
D) P and Q are wrong
Solution:
B) P correct Q wrong.
Lengths and breadths of a rectangle can change for the same perimeter. But, the side of a square cannot change for the same perimeter.