SCERT AP 10th Class Maths Textbook Solutions Chapter 7 నిరూపక రేఖాగణితం Intext Questions Textbook Exercise Questions and Answers.
AP State Syllabus 10th Class Maths Solutions 7th Lesson నిరూపక రేఖాగణితం InText Questions
ఇవి చేయండి:
ప్రశ్న 1.
క్రింది పటం నుండి A, B, C, D, E, F, G, H బిందువుల నిరూపకాలు కనుగొనండి. (పేజీ నెం. 159)
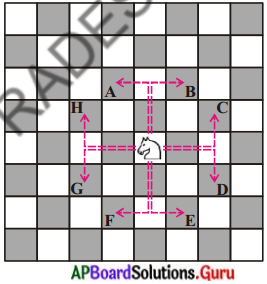
సాధన.
గుర్రం యొక్క స్థానం మూల బిందువుగా ఉందనుకోవాలి.
A (- 1, 2), B (1, 2), C (2, 1), D (2, – 1), E (1, – 2), F (- 1, – 2), G (- 2, – 1), H (- 2, 1).
![]()
ప్రశ్న 2.
8 కదలికల తర్వాత గుఱ్ఱం కదిలిన దూరం కనుగొనండి. అనగా మూలబిందువు (0, 0) నుండి A, B, C, D, E, F, G, H బిందువుల మధ్య దూరంను కనుగొనండి. (పేజీ నెం. 159)
సాధన.
గుర్రం (0, 0) నుండి, A కి కదిలిన దూరం + B కి కదిలిన దూరం + ……… + H కి కదిలిన దూరం
= 3 + 3 + 3 + 3 + 3 + 3 + 3 + 3
= 24 యూనిట్లు .
ప్రశ్న 3.
బిందువులు H మరియు C ల మధ్య దూరమెంత ? అలాగే బిందువులు A మరియు B ల మధ్య దూరమెంత? (పేజీ నెం. 159).
సాధన.
H మరియు C ల మధ్య దూరం = 4 యూనిట్లు
A మరియు B ల మధ్యదూరం = 2 యూనిట్లు
ప్రశ్న 4.
(- 4, 0), (2, 0), (6, 0), (-8, 0) బిందువులు నిరూపక తలంలో ఎక్కడ ఉంటాయి ? (పేజీ నెం. 160)
సాధన.
ఇచ్చిన అన్ని బిందువులు X – అక్షంపై ఉంటాయి.
![]()
ప్రశ్న 5.
(- 4, 0), (6, 0) బిందువుల మధ్య దూరమెంత ? (పేజీ నెం. 160)
సాధన.
(- 4, 0), 16, 0) బిందువులు X – అక్షంపై ఉంటాయి.
కావున వాని మధ్య దూరం = |x2 – x1|
= |6 – (- 4)| = |6 + 4| = 10 యూనిట్లు.
ప్రశ్న 6.
కింది బిందువుల మధ్య దూరం కనుగొనండి. (పేజీ నెం. 162)
(i) (3, 8), 16, 8)
సాధన.
బిందువుల మధ్య దూరం = |x2 – x1|
(∵ రెండు బిందువులలో Y నిరూపకాలు సమానం)
= | 6 -3 | = 3 యూనిట్లు..
(ii) (- 4, – 3), (- 8, – 3)
సాధన.
బిందువుల మధ్య దూరం = |x2 – x1| (∵ రెండు బిందువులలో Y నిరూపకాలు సమానం)
= | – 8 – (- 4) | = | – 8 + 4 |
= | – 4 | = 4 యూనిట్లు.
(iii) (3, 4), (3, 8)
సాధన.
బిందువుల మధ్య దూరం = |y2 – y1| (∵ రెండు బిందువులలో X నిరూపకాలు సమానం)
= | 8 – 4 | = 4 యూనిట్లు.
(iv) (- 5, – 8), (- 5, – 12)
సాధన.
బిందువుల మధ్య దూరం = |y2 – y1|
= |- 12 – (- 8)|
= |- 12 + 8| ( ∵ రెండు బిందువులలో X నిరూపకాలు సమానం)
= | – 4 | = 4 యూనిట్లు.
![]()
ప్రశ్న 7.
కింది బిందువుల మధ్య దూరం కనుగొనండి. (పేజీ నెం. 162)
(i) A (2, 0) మరియు B (0, 4)
సాధన.
A (2, 0) X – అక్షంపైన,
B (0, 4) Y – అక్షం పైన ఉంటాయి.
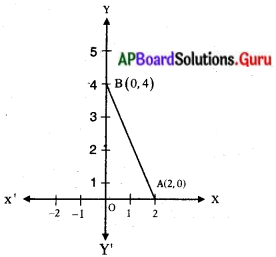
∆AOB లంబకోణ త్రిభుజము
OA = 2; OB = 4
AB2 = OA2 + OB2
AB2 = (2)2 + (4)2
AB = √(4 + 16) = √20 = 2√5
గమనిక : (x1, 0), (0, y1) బిందువుల మధ్య దూరం = √(x12 + y12).
(ii) P(0, 5) మరియు Q (12, 0)
సాధన.
P (0, 5) మరియు Q (12, 0) .
P, Q ల మధ్య దూరం = \(\sqrt{(12)^{2}+(5)^{2}}\)
= \(\sqrt{144+25}=\sqrt{169}\) = 13
P, Q ల మధ్య దూరం = 13 యూనిట్లు.
ప్రశ్న 8.
కింద ఇవ్వబడిన బిందువుల మధ్య దూరం కనుగొనండి. (పేజీ నెం. 164)
(i) (7, 8) మరియు ( – 2, 3)
సాధన.
A (7, 8) మరియు B (- 2, 3)
A, B ల మధ్య దూరం = \(\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)
= \(\sqrt{(-2-7)^{2}+(3-8)^{2}}\)
= \(\sqrt{(-9)^{2}+(-5)^{2}}=\sqrt{81+25}=\sqrt{106}\)
(ii) (- 8, 6) మరియు (2,0)
సాధన.
A (- 8, 6) మరియు B (2, 0)
X = – 8, x, = 2, y = 6, y) = 0
A, B ల మధ్య దూరం = \(\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)
= \(\sqrt{(2-(-8))^{2}+(0-6)^{2}}\)
= \(\sqrt{10^{2}+(-6)^{2}}=\sqrt{100+36}\)
= √136.
![]()
ప్రయత్నించండి:
ప్రశ్న 1.
(0, – 3), (0, – 8), (0, 6), (0, 4) బిందువులు నిరూపక తలంలో ఎక్కడ ఉంటాయి ? (పేజీ నెం. 161)
సాధన.
అన్ని బిందువులు Y – అక్షంపై ఉంటాయి.
ప్రశ్న 2.
(0, – 3) మరియు (0, – 8) బిందువుల మధ్య దూరమెంత ? అలాగే Y – అక్షంపై ఉన్న బిందువుల మధ్యదూరం | y2 – y1| అవుతుందని చెప్పగలవా ? (పేజీ నెం. 161)
సాధన.
(0, – 3), (0, – 8) లు Y – అక్షంపై గల బిందువులు.
వీని మధ్యదూరం= |y2 – y1|
= |- 8 – (- 3)| = |- 8 + 3| = |- 5 | యూనిట్లు
Y – అక్షంపై గల బిందువుల మధ్య దూరం = |y2 – y1| అవుతుంది.
ప్రశ్న 3.
మూలబిందువు ‘0’ మరియు బిందువు A (7, 4) ల మధ్యదూరం కనుగొనండి. (పేజీ నెం. 162)
సాధన.
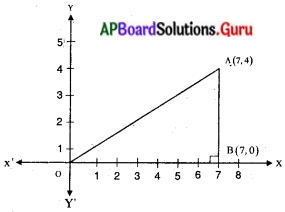
పై పటం నుండి AB = 4 యూనిట్లు, OB = 7 యూనిట్లు
∆ABO లంబకోణ త్రిభుజము
OA2 = OB2 + BA2
= 72 + 42 = 49 + 16
OA2 = 65
OA = √65 యూనిట్లు.
గమనిక :
మూలబిందువు (0, 0) నుండి (x1, y1) బిందువుకు గల దూరము \(\sqrt{x_{1}^{2}+y_{1}^{2}}\).
మూలబిందువు నుండి A (7, 4) కు గల దూరం = \(\sqrt{7^{2}+4^{2}}=\sqrt{49+16}=\sqrt{65}\) యూనిట్లు.
![]()
ప్రశ్న 4.
ఒక రేఖాఖండం \(\overline{\mathrm{AB}}\) యొక్క తొలి, చివరి బిందువులు A(1, – 3) మరియు B(- 4, 4) అయిన AB మధ్య దూరాన్ని దగ్గరి దశాంశాలకు కనుగొనండి. (పేజీ నెం. 164)
సాధన.
A (1, – 3) మరియు B (- 4, 4) ..
x1 = 1, x2 = – 4, y1 = – 3, y2 = 4
AB ల మధ్య దూరం, d = \(\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)
= \(\sqrt{(-4-1)^{2}+(4-(-3))^{2}}\)
= \(\sqrt{(-5)^{2}+(7)^{2}}\)
= \(\sqrt{25+49}=\sqrt{74}\)
AB ల మధ్య దూరం = 8.602
![]()
ఆలోచించి, చర్చించి, రాయండి:
ప్రశ్న 1.
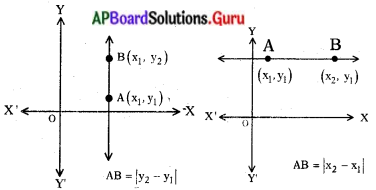
రెండు బిందువులలోని X లేదా 5 నిరూపకాలు సమానంగా (0 కాకుండా) ఉంటే వాటి మధ్యదూరం ఎలా కనుగొంటావు ? (పేజీ నెం, 161)
సాధన.
సందర్భం – 1:
రెండు బిందువులలోని x నిరూపకాలు సమానంగా ఉంటే ఆ రెండు బిందువులు Y- అక్షానికి సమాంతరంగా గల రేఖపై ఉంటాయి.
కావున రెండు బిందువులలోని y నిరూపకాల భేదం |Y2 – Y1| ఆ రెండు బిందువుల మధ్య దూరం అవుతుంది.
(x1, y1), (x2, y2) బిందువుల మధ్య దూరం = |y2 – y1|
సందర్భం – 2:
రెండు బిందువులలోని y నిరూపకాలు సమానం అయితే ఆ బిందువులు X – అక్షానికి సమాంతరంగా గల రేఖపై ఉంటాయి. కావున ఈ రెండు బిందువులలోని X నిరూపకాల భేదం |x2 – x1| ఆ రెండు బిందువుల మధ్య దూరం అవుతుంది.
(x1, y1), (x2, y2) బిందువుల మధ్య దూరం = |x2 – x1|
![]()
ప్రశ్న 2.
రెండు బింధువులు నిరూపకతలంలోని వేర్వేరు పాదాలలో ఉంటే వాటి మధ్య దూరం ఎలా కనుగొంటారు? (పేజీ నెం. 163)
సాధన.
A, B అనే రెండు బిందువులు వేర్వేరు తలాలలో ఉంటే A, Bల మధ్య దూరాన్ని కనుగొనడానికి, A, B బిందువుల గుండా అక్షాలకు లంబ రేఖలను గీచి, \(\overline{\mathrm{AB}}\) కర్ణంగా గల లంబకోణ త్రిభుజాన్ని ఏర్పరచాలి. అలా ఏర్పడిన లంబకోణ త్రిభుజం యొక్క కర్ణం పొడవును పైథాగరస్ సిద్ధాంతాన్ని ఉపయోగించి కనుగొంటాము. ఈ పొడవే A, B ల మధ్య దూరం అవుతుంది.
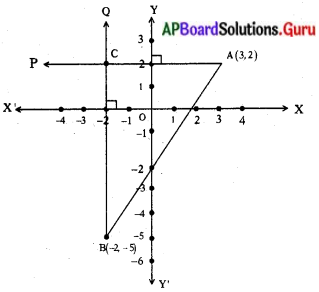
ఉదాహరణకు A(3, 4), B(- 2, – 5) లు వరుసగా 1వ, 3వ పాదాలలో కలవు. వీని మధ్యదూరం కనుగొందాము.
సాధన.
A (3, 2) గుండా Y – అక్షానికి లంబం AP, B (- 2, – 5) గుండా X – అక్షానికి లంబం BQ లను గీయాలి. వీటి ఖండన బిందువు C అవుతుంది.
ఇప్పుడు AC = 5 యూనిట్లు
BC = 7 యూనిట్లు .
లంబకోణ త్రిభుజం ∆ABCలో AB2 = AC2 + BC2 (పైథాగరస్ సిద్ధాంతము)
= 52 + 72
AB2 = 25 + 49 = 74
AB = √74 యూనిట్లు
గమనిక : A (x1, y1), B (x2, y2) బిందువుల మధ్యదూరం సూత్రం రాబట్టిన తర్వాత అయితే రెండు బిందువుల మధ్య దూరం సూత్రం
d = \(\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\) ను ఉపయోగించి ఒకే తలంలో గల ఏ రెండు బిందువుల మధ్య దూరాన్నైనా కనుగొనవచ్చును.
![]()
ప్రశ్న 3.
రాము, బిందువు P(x, y) మరియు మూలబిందువు O(0, 0)ల మధ్య దూరం \(\sqrt{x^{2}+y^{2}}\) అని తెలిపెను. నీవు రాము తెలిపిన దానితో ఏకీభవిస్తున్నావా? లేదా? ఎందుకు ? (పేజీ నెం. 163)
సాధన.
రాముతో ఏకీభవిస్తాను.
O(0, 0), P(x, y) ల మధ్య దూరం d = \(\sqrt{(x-0)^{2}+(y-0)^{2}}\)
= \(\sqrt{x^{2}+y^{2}}\)
ఈ విలువ రాము సమాధానంతో సరిపోతున్నది. కావున రాముతో ఏకీభవిస్తున్నాను.
(లేదా)
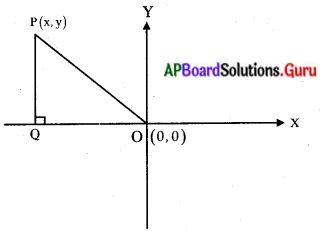
పై పటం నుండి, ∆PQO లంబకోణ త్రిభుజము.
PQ = y, QQ = x
OP2 = OQ2 + QP2
= x2 + y2
OP = √(x2 + y2)
ఈ విలువ, రాము సమాధానము ఒకటే. కావున ‘ రాము సమాధానంతో ఏకీభవిస్తాను.
ప్రశ్న 4.
రాము రెండు బిందువుల మధ్య దూరాన్ని ఈ విధంగా రాశాడు. AB = \(\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\) ఎందుకు ? (పేజీ నెం. 163)
సాధన.
A(x1, y1), B(x2, y2) బిందువుల మధ్య దూరం \(\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\) కు సమానం.
A, B బిందువుల మధ్య దూరాన్ని AB గా రాస్తాము.
కావున AB = \(\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\) అని రాశాడు.
![]()
ప్రశ్న 5.
శ్రీధర్ రెండు బిందువులు T (5, 2) మరియు R (- 4, – 1) ల మధ్య దూరం 9.5 యూనిట్లుగా లెక్కించాడు. ఇపుడు మీరు రెండు బిందువులు P (4, 1) మరియు Q (-5, – 2) ల మధ్య దూరాన్ని కనుగొనండి. మీరు కూడా శ్రీధర్ పొందిన సమాధానాన్నే పొందారా ? ఎందుకు ? (పేజీ నెం. 164)
సాధన.
P(4, 1), Q (- 5, – 2) బిందువుల మధ్య దూరం
రెండు బిందువుల మధ్య దూరం PQ = \(\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)
= \(\sqrt{(-5-4)^{2}+(-2-1)^{2}}\)
= \(\sqrt{(-9)^{2}+(-3)^{2}}\)
= \(\sqrt{81+9}=\sqrt{90}\)
= 3√10 = 3√2 × √5
= 3 × 1.414 × 2.236 [∵ √2 = 1.413, √5 = 2.236]
PQ = 9.4851 = 9.5
PQ = 9.4851ను ఒక దశాంశానికి సవరించినపుడు మనం కూడా శ్రీధర్ పొందిన సమాధానాన్నే పొందుతున్నాము.
T (5, 2), R (- 4, – 1) బిందువులలోని x, y నిరూపకాల యొక్క గుర్తులను మార్చగా P (4, 1) మరియు Q (- 5, – 2) వస్తున్నాయి.
కాబట్టి TR = PQ అవుతుంది.
గమనిక :
P (x1, y1), Q (x2, y2) మరియు R(- x1, – y1), S (- x2, – y2) అయిన PQ = RS అగును.
![]()
ఇవి చేయండి:
ప్రశ్న 1.
బిందువులు (3, 5) మరియు (8, 10) లచే ఏర్పడు రేఖాఖండమును 2:3 నిష్పత్తిలో అంతరంగా విభజించు బిందువును కనుగొనండి. (పేజీ నెం. 171)
సాధన.
ఇచ్చిన బిందువులు (3, 5), (8, 10) లను 2 : 3 నిష్పత్తిలో విభజించే బిందువు P (x, y) అనుకుందాం.
విభజించే సూత్రం – P(x, y) = \(=\left(\frac{m_{1} x_{2}+m_{2} x_{1}}{m_{1}+m_{2}}, \frac{m_{1} y_{2}+m_{2} y_{1}}{m_{1}+m_{2}}\right)\)
= \(\left(\frac{2(8)+3(3)}{2+3}, \frac{2(10)+1(5)}{2+3}\right)\)
= \(\left(\frac{16+9}{5}, \frac{20+5}{5}\right)\)
= (\(\frac{25}{5}\), \(\frac{25}{5}\)) = (5, 5)
∴ కావలసిన బిందువు P(x, y) = (5, 5)
ప్రశ్న 2.
బిందువులు (2, 7) మరియు (12, -7) లచే ఏర్పడు రేఖాఖండం యొక్క మధ్యబిందువును కనుగొనండి. (పేజీ నెం. 171)
సాధన.
(2, 7), (12, – 7) బిందువుల మధ్య బిందువు M (x, y) అనుకొనుము.
(x1, y1), (x2, y2) బిందువులతో ఏర్పడు రేఖ యొక్క మధ్యబిందువు నిరూపకాలు M(x,y) అనుకొనుము.
M(x, y) = \(\left(\frac{x_{1}+x_{2}}{2}, \frac{y_{1}+y_{2}}{2}\right)\)
= \(\left(\frac{2+12}{2}, \frac{7+(-7)}{2}\right)\)
= \(\left(\frac{14}{2}, \frac{0}{2}\right)\) = (7, 0)
కావలసిన బిందువు M(x, y) = (7,0) .
![]()
ప్రశ్న 3.
బిందువులు (- 4, 6), (2, -2 ) మరియు (2, 5)లు శీర్షాలుగా గల త్రిభుజం యొక్క గురుత్వ కేంద్రంను కనుగొనండి. (పేజీ నెం. 173)
సాధన.
గురుత్వ కేంద్ర నిరూపకాలు = \(\left(\frac{x_{1}+x_{2}+x_{3}}{3}, \frac{y_{1}+y_{2}+y_{3}}{3}\right)\)
= \(\left(\frac{-4+2+2}{3}, \frac{6+(-2)+5}{3}\right)\)
= \(\left(\frac{-4+4}{3}, \frac{11-2}{3}\right)\)
= (0, \(\frac{9}{3}\)) = (0, 3)
∴ గురుత్వ కేంద్రం (0, 3)
ప్రశ్న 4.
బిందువులు (2, – 6) మరియు ( 4, 8) లను కలుపు రేఖాఖండం యొక్క త్రిథాకరణ బిందువులను కనుగొనండి. (పేజీ నెం. 175)
సాధన.
ఇచ్చిన బిందువులు A (2, – 6), B (- 4, 8).
A(2, – 6), B(- 4, 8) లను కలుపు రేఖాఖండము యొక్క త్రిథాకరణ బిందువులు P, Q అనుకుందాం.
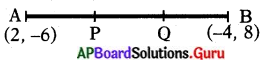
\(\overline{\mathrm{AB}}\) రేఖాఖండాన్ని P 1 : 2 నిష్పత్తిలో విభజిస్తుంది.
∴ P(x, y) = \(\left(\frac{m_{1} x_{2}+m_{2} x_{1}}{m_{1}+m_{2}}, \frac{m_{1} y_{2}+m_{2} y_{1}}{m_{1}+m_{2}}\right)\)
= \(\left(\frac{1(-4)+2(2)}{1+2}, \frac{1(8)+2(-6)}{1+2}\right)\)
= \(\left(\frac{-4+4}{3}, \frac{8-12}{3}\right)=\left(\frac{0}{3}, \frac{-4}{3}\right)\)
= (1-4+2[2] 18 +2-))
∴ P = (0, \(\frac{-4}{3}\))
ఇపుడు \(\overline{\mathrm{AB}}\) రేఖాఖండాన్ని Q 2 : 1 నిష్పత్తిలో విభజిస్తుంది.
Q (x, y) = \(\left(\frac{2(-4)+1(2)}{2+1}, \frac{2(8)+1(-6)}{2+1}\right)\)
= \(\left(\frac{-8+2}{3}, \frac{16-6}{3}\right)\)
= \(\left(\frac{-6}{3}, \frac{10}{3}\right)=\left(-2, \frac{10}{3}\right)\)
∴ Q = (- 2, \(\frac{10}{3}\)) కావున (2, – 6) మరియు (- 4, 8) లను కలిపే రేఖాఖండం యొక్క త్రిథాకరణ బిందువులు (0, \(-\frac{4}{3}\)) మరియు (- 2, \(\frac{10}{3}\)).
సరిచూచుకోవడం :
(i) \(\overline{\mathrm{AB}}\) యొక్క త్రిథాకరణ బిందువులు P, Q అయిన A, Bల మధ్యబిందువు, P, Qల మధ్యబిందువు ఒకటే అవుతుంది.
A, B ల మధ్య బిందువు = \(\left(\frac{x_{1}+x_{2}}{2}, \frac{y_{1}+y_{2}}{2}\right)\)
= \(\left(\frac{2+(-4)}{2}, \frac{-6+8}{2}\right)=\left(\frac{-2}{2}, \frac{2}{2}\right)\) = (-1.1)
P, Qల మధ్య బిందువు = \(\left(\frac{0+(-2)}{2}, \frac{\frac{-4}{3}+\frac{10}{3}}{2}\right)\)
= \(\left(\frac{-2}{2}, \frac{\frac{6}{3}}{2}\right)=\left(-1, \frac{2}{2}\right)\) = (- 1, 1)
(ii) AP, PQ, QB పొడవులను కనుగొని కూడా సరిచూచుకోవచ్చును.
AP = PQ = QB అవుతాయి.
![]()
ప్రశ్న 5.
బిందువులు (- 3, – 5), (- 6, – 8) లను కలుపు రేఖండము యొక్క త్రిథాకరణ బిందువులను కనుగొనుము. (పేజీ నెం. 175)
సాధన.
బిందువులు A (- 3, – 5), B (- 6, – 8) లను కలుపు రేఖాఖండము యొక్క ప్రాథాకరణ బిందువులు P, Q అనుకొంటే \(\overline{\mathrm{AB}}\) ను P 1 : 2 నిష్పత్తిలో అంతరంగా విభజిస్తుంది.
P(x, y) = \(\left(\frac{m_{1} x_{2}+m_{2} x_{1}}{m_{1}+m_{2}}, \frac{m_{1} y_{2}+m_{2} y_{1}}{m_{1}+m_{2}}\right)\)
= \(\left(\frac{1(-6)+2(-3)}{1+2}, \frac{1(-8)+2(-5)}{1+2}\right)\)
= \(\left(\frac{-6-6}{3}, \frac{-8-10}{3}\right)=\left(\frac{-12}{3}, \frac{-18}{3}\right)\)
= (- 4, – 6)
∴ P = (- 4, – 6)
ఇప్పుడు \(\overline{\mathrm{AB}}\) ని Q 2 : 1 నిష్పత్తిలో అంతరంగా విభజిస్తుంది.
Q(x, y) = \(\left(\frac{2(-6)+1(-3)}{2+1}, \frac{2(-8)+1(-5)}{2+1}\right)\)
= \(\left(\frac{-12-3}{3}, \frac{-16-5}{3}\right)=\left(\frac{-15}{3}, \frac{-21}{3}\right)\)
= (- 5 – 7)
Q = (- 5, – 7)
కావున బిందువులు (- 3, – 5), (- 6, – 8) లను కలుపు రేఖాఖండం యొక్క త్రిథాకరణ బిందువులు (- 4, – 6) మరియు Q (- 5, – 7)
సరిచూచుకొనుట :
A, B మధ్యబిందువు = \(\left(\frac{(-3)+(-6)}{2}, \frac{(-5)+(-8)}{2}\right)\)
= \(\left(\frac{-9}{2}, \frac{-13}{2}\right)\)
P, Q మధ్యబిందువు = \(\left(\frac{(-4)+(-5)}{2}, \frac{(-6)+(-7)}{2}\right)\)
= \(\left(\frac{-9}{2}, \frac{-13}{2}\right)\)
![]()
కృత్యము:
బిందువులు A(4, 2), B(6, 5) మరియు C(1, 4) లు ∆ABC యొక్క శీర్షాలు.
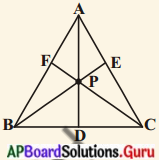
ప్రశ్న 1.
A నుండి BC పైకి గీసిన మధ్యగతరేఖ D వద్ద కలుస్తుంది. అయిన D బిందువు నిరూపకాలు కనుగొనండి. (పేజీ నెం. 172)
సాధన.
B (6, 5) మరియు C(1, 4) ల మధ్యబిందువు
D(x, y) = \(\left(\frac{x_{1}+x_{2}}{2}, \frac{y_{1}+y_{2}}{2}\right)\)
= \(\left(\frac{6+1}{2}, \frac{5+4}{2}\right)=\left(\frac{7}{2}, \frac{9}{2}\right)\).
ప్రశ్న 2.
AP : PD = 2 : 1 అయ్యే విధంగా AD రేఖపై P బిందువు నిరూపకాలను కనుగొనండి. (పేజీ నెం. 172)
సాధన.
A(4, 2), D\(\left(\frac{7}{2}, \frac{9}{2}\right)\) లను 2 : 1 నిష్పత్తిలో -విభజించే బిందువు
∴ P = \(\left(\frac{\mathrm{m}_{1} \mathrm{x}_{2}+\mathrm{m}_{2} \mathrm{x}_{1}}{\mathrm{~m}_{1}+\mathrm{m}_{2}}, \frac{\mathrm{m}_{1} \mathrm{y}_{2}+\mathrm{m}_{2} \mathrm{y}_{1}}{\mathrm{~m}_{1}+\mathrm{m}_{2}}\right)\)
= \(\left(\frac{2\left(\frac{7}{2}\right)+1(4)}{2+1}, \frac{2\left(\frac{9}{2}\right)+1(2)}{2+1}\right)\)
= \(\left(\frac{7+4}{3}, \frac{9+2}{3}\right)\)
⇒ P = \(\left(\frac{11}{3}, \frac{11}{3}\right)\)
![]()
ప్రశ్న 3.
BE రేఖను 2 : 1 నిష్పత్తిలో విభజించు బిందువును మరియు CF రేఖను 2 : 1 నిష్పత్తిలో విభజించు బిందువును కనుగొనండి. (పేజీ నెం. 172)
సాధన.
A(4, 2), C (1, 4) ల మధ్య బిందువు E = \(\left(\frac{4+1}{2}, \frac{2+4}{2}\right)=\left(\frac{5}{2}, 3\right)\)
A(4, 2), B (6, 5) ల మధ్య బిందువు F = \(\left(\frac{4+6}{2}, \frac{2+5}{2}\right)=\left(5, \frac{7}{2}\right)\)
(i) B(6, 5), E(\(\frac{5}{2}\). 3) లను 2 : 1 నిష్పత్తిలో విభజించే బిందువు
Q = \(\left(\frac{\mathrm{m}_{1} \mathrm{x}_{2}+\mathrm{m}_{2} \mathrm{x}_{1}}{\mathrm{~m}_{1}+\mathrm{m}_{2}}, \frac{\mathrm{m}_{1} \mathrm{y}_{2}+\mathrm{m}_{2} \mathrm{y}_{1}}{\mathrm{~m}_{1}+\mathrm{m}_{2}}\right)\)
= \(\left(\frac{2\left(\frac{5}{2}\right)+1(6)}{2+1}, \frac{2(3)+1(5)}{2+1}\right)\)
= \(\left(\frac{5+6}{3}, \frac{6+5}{3}\right)\)
⇒ Q = \(\left(\frac{11}{3}, \frac{11}{3}\right)\)
(ii) C(1, 4), F(5,7) లను 2 : 1 నిష్పత్తిలో విభజించే బిందువు
R = \(\left(\frac{2(5)+1(1)}{2+1}, \frac{2\left(\frac{7}{2}\right)+1(4)}{2+1}\right)\)
= \(\left(\frac{10+1}{3}, \frac{7+4}{3}\right)\)
⇒ R = (11 11)
ప్రశ్న 4.
మీరేమి గమనించారు ? “ఒక త్రిభుజంలోని ప్రతి మధ్యగతరేఖను 2 : 1 నిష్పత్తిలో విభజించు బిందువు ఆ త్రిభుజం యొక్క గురుత్వకేంద్రం అవుతుంది”. (పేజీ నెం. 172)
సాధన.
మధ్యగతాలను 2 : 1 నిష్పత్తిలో విభజించే బిందువులు P, Q, Rలు ఏకీభవిస్తున్నాయి. మధ్యగతరేఖల మిళిత బిందువును గురుత్వ కేంద్రము అంటామని మనకు తెలుసు. P, Q, R లు ఈ గురుత్వ కేంద్రంతో ఏకీభవిస్తున్నాయి.
“అనగా “ఒక. త్రిభుజంలోని ప్రతి మధ్యగత రేఖను 2 : 1 నిష్పత్తిలో విభజించు బిందువు ఆ త్రిభుజం యొక్క గురుత్వ కేంద్రము అవుతుంది”.
![]()
ప్రయత్నించండి:
బిందువులు (2, 3), (x, y), (3, -2 ) లు శీర్షాలుగా గల త్రిభుజం యొక్క గురుత్వ కేంద్రం మూలబిందువు అయిన (x, y) లను కనుగొనండి.(పేజీ నెం. 173)
సాధన.
ఇచ్చినది (2, 3), (x, y), (3, -2) లు త్రిభుజ శీర్షాలు గురుత్వ కేంద్రం = (0,0)
అనగా
\(\left(\frac{x_{1}+x_{2}+x_{3}}{3}, \frac{y_{1}+y_{2}+y_{3}}{3}\right)\) = (0, 0)
\(\left(\frac{2+x+3}{3}, \frac{3+y+(-2)}{3}\right)\) = (0, 0)
\(\left(\frac{5+x}{3}, \frac{y+1}{3}\right)\) = 0
⇒ 5 + x = 0
⇒ x = – 5
⇒ y + 1 = 0
⇒ y = – 1
∴ (x, y) = (- 5, – 1).
![]()
అలోచించి, చర్చించి, రాయండి:
బిందువులు A(6, 9) మరియు B(- 6, – 9) లను కలుపు రేఖాఖందమును. (పేజీ నెం. 174)
(a) మూలబిందువు ఏ నిష్పత్తిలో విభజిస్తుంది ? ఆ రేఖా ఖండమునకు మూలబిందువును ఏమంటారు ?
సాధన.
ఇచ్చిన బిందువులు : A (6, 9), B (- 6, – 9) లను మూలబిందువు m1 : m2 నిష్పత్తిలో విభిజిస్తుందని అనుకొందాం.
(0, 0) = \(\left(\frac{\mathrm{m}_{1}(-6)+\mathrm{m}_{2}(6)}{\mathrm{m}_{1}+\mathrm{m}_{2}}, \frac{\mathrm{m}_{1}(-9)+\mathrm{m}_{2}(9)}{\mathrm{m}_{1}+\mathrm{m}_{2}}\right)\)
(0, 0) = \(\left(\frac{-6 m_{1}+6 m_{2}}{m_{1}+m_{2}}, \frac{-9 m_{1}+9 m_{2}}{m_{1}+m_{2}}\right)\)
∴ \(\frac{-6 m_{1}+6 m_{2}}{m_{1}+m_{2}}\) = 0
– 6m1 + 6m2 = 0
– 6m1 = – 6m2
⇒ 6m1 = 6m2
⇒ \(\frac{m_{1}}{m_{2}}=\frac{6}{6}=\frac{1}{1}\)
m1 : m2 = 1 : 1
∴ కావలసిన నిష్పత్తి = 1 : 1.
A, B బిందువులను మూలబిందువు 1 : 1 నిష్పత్తిలో విభజిస్తుంది.
కావున మూలబిందువును AB రేఖాఖండానికి మధ్యబిందువు అంటారు.
(b) బిందువు P(2, 3) ఏ నిష్పత్తిలో విభజిస్తుంది ?
సాధన.
A (6, 9), B (- 6, – 9) ను P (2, 3) m1 : m2 నిష్పత్తిలో విభజిస్తుంది అనుకొందాం. 1) 1 ( m (-6) + ma(6) ma (-9) + ma(9)]
(2, 3) = \(\left(\frac{\mathrm{m}_{1}(-6)+\mathrm{m}_{2}(6)}{\mathrm{m}_{1}+\mathrm{m}_{2}}, \frac{\mathrm{m}_{1}(-9)+\mathrm{m}_{2}(9)}{\mathrm{m}_{1}+\mathrm{m}_{2}}\right)\)
(2, 3) = \(\left(\frac{-6 m_{1}+6 m_{2}}{m_{1}+m_{2}}, \frac{-9 m_{1}+9 m_{2}}{m_{1}+m_{2}}\right)\)
∴ 2 = \(\frac{-6 m_{1}+6 m_{2}}{m_{1}+m_{2}}\)
⇒ 2m1 + 2m2 = – 6m1 + 6m2
⇒ 8m1 = 4m2
\(\frac{m_{1}}{m_{2}}=\frac{4}{8}=\frac{1}{2}\)
m1 : m2 = 1 : 2
![]()
(c) బిందువు Q(- 2, – 3) ఏ నిష్పత్తిలో విభజిస్తుంది ?
సాధన.
A (6, 9), B (- 6, – 9) లను Q (- 2, – 3) విభజించే నిష్పత్తి m1 : m2 అనుకొనుము.
(- 2, – 3) = \(\left(\frac{-6 m_{1}+6 m_{2}}{m_{1}+m_{2}}, \frac{-9 m_{1}+9 m_{2}}{m_{1}+m_{2}}\right)\)
∴ – 2 = \(\frac{-6 m_{1}+6 m_{2}}{m_{1}+m_{2}}\)
⇒ – 2m1 – 2m2 = – 6m1 + 6m2
4m1 = 8m2
\(\frac{\mathrm{m}_{1}}{\mathrm{~m}_{2}}=\frac{8}{4}=\frac{2}{1}\)
∴ m1 : m2 = 2 : 1
(d) బిందువులు P, Qలు AB ని ఎన్ని సమాన భాగాలుగా విభజిస్తాయి ?
సాధన.
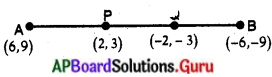
బిందువులు P, Q \(\overline{\mathrm{AB}}\) ని 3 సమాన భాగాలుగా విభజిస్తాయి.
(e) P, Q లను ఏమంటారు ?
సాధన.
P, Q లను AB యొక్క సమత్రిఖండన బిందువులని అంటారు. ఈ సమత్రిఖండన బిందువులను త్రిథాకరణ బిందువులని పిలుస్తాము.
![]()
ఇవి చేయండి:
కింద ఇవ్వబడిన శీర్షాలు గల త్రిభుజ వైశాల్యం కనుగొనండి. (పేజీ నెం. 180)
ప్రశ్న 1.
(5, 2) (3, – 5) మరియు (- 5, -1 )
సాధన.
బిందువులు: (5, 2), (3, – 5), మరియు (- 5, – 1) లు శీర్షాలుగా గల త్రిభుజ వైశాల్యం ∆ = \(\frac{1}{2}\) |x1 (y2 – y3) + x2 (y3 – y1) + x3 (y2 – y1)|
= \(\frac{1}{2}\) |5(- 5 – (- 1) + 3((- 1) – 2) + (- 5) (2 – (- 5))|
= \(\frac{1}{2}\) |(- 5 + 1) + 3(- 3) + – 5(2 + 5)|
= \(\frac{1}{2}\) |- 20 – 9 – 35|
= \(\frac{1}{2}\) |- 64|
= \(\frac{1}{2}\) × 64 = 32 చ.యూ.
ప్రశ్న 2.
(6, – 6), (3, – 7) మరియు (3, 3) (పేజీ నెం. 180)
సాధన.
(6, – 6), (3, – 7) మరియు (3, 3) లు శీర్షాలుగా గల త్రిభుజ వైశాల్యం = \(\frac{1}{2}\) |6(- 7 – 3) +3(3 – (- 6)) + 3(- 6 – (- 7))|
= \(\frac{1}{2}\) | 6(- 10) + 3(9) + 3(1)|
= \(\frac{1}{2}\) |- 60 + 27 + 3|
= \(\frac{1}{2}\) |- 30|
= \(\frac{1}{2}\) × 30 = 15 చ.యూ.
![]()
ప్రశ్న 3.
కింద ఇవ్వబడిన బిందువులు సరేఖీయాలు అవుతాయా? కావా ? సరి చూడండి. (పేజీ నెం. 182)
(i) (1, – 1), (4, 1), (- 2, – 3)
సాధన.
ఇచ్చిన బిందువులు = (1, – 1), (4, 1), (- 2, – 3) లతో ఏర్పడే త్రిభుజ వైశాల్యం = \(\frac{1}{2}\) |x1 (y2 – y3) + x2 (y3 – y1) + x3 (y2 – y1)|
= \(\frac{1}{2}\) |1[1 – (- 3)] + 4[- 3 – (- 1) + (- 2)[- 1 – 1]|
= \(\frac{1}{2}\) |1(4) + 4 (- 2) – 2 (- 2)|
= \(\frac{1}{2}\) |4 – 8 + 4|
= \(\frac{1}{2}\) |0| = 0
∴ త్రిభుజ వైశాల్యము సున్న ‘0’ కావున ఇచ్చిన బిందువులు సరేఖీయాలు.
(ii) (1, -1), (2, 3), (2, 0)
సాధన.
(1, – 1), (2, 3), (2, 0) బిందువులతో ఏర్పడే త్రిభుజ వైశాల్యం
= \(\frac{1}{2}\) | 1(3 – 0) + 2[0 – (- 1)] +2(- 1 – 3)|
= \(\frac{1}{2}\) |3 + 2 – 8|
= \(\frac{1}{2}\) |5 – 8|
= \(\frac{1}{2}\) |- 3|
= \(\frac{1}{2}\) × 3
= \(\frac{3}{2}\) చ.యూ.
∴ త్రిభుజ వైశాల్యము \(\frac{3}{2}\) చ.యూ. కావున ఇచ్చిన మూడు బిందువులు సరేఖీయాలు కావు.
![]()
(iii) (1, – 6), (3, – 4), (4, – 3)
సాధన.
(1, – 6), (3, – 4), (4, – 3) లతో ఏర్పడే త్రిభుజ వైశాల్యం
= \(\frac{1}{2}\) |1[- 4 – (- 3)] + 3[- 3 – (- 6)] + [- 6 – (- 4)]|
= \(\frac{1}{2}\) |1[- 4 + 3] + 3[- 3 + 6] + 4(- 6 – 4)|
= \(\frac{1}{2}\) |1 (- 1) + 3 (3) + 4 (- 2)|
= \(\frac{1}{2}\) |- 1 + 9 – 8|
= \(\frac{1}{2}\) |9 – 9| = 0
∴ త్రిభుజ వైశాల్యము సున్న’ ‘0’ కావున ఇచ్చిన మూడు బిందువులు సరేఖీయాలు.
ప్రశ్న 4.
15 మీ, 17 మీ, 21 మీ భుజాలుగా గల త్రిభుజం వైశాల్యం (హెరాన్ సూత్రం ద్వారా) కనుగొనండి. (పేజీ నెం. 189)
సాధన.
ఇచ్చిన త్రిభుజ భుజాలు
a = 15 మీ b = 17 మీ. మరియు c = 21 మీ.
∴ s =\(\frac{a+b+c}{2}=\frac{15+17+21}{2}=\frac{53}{2}\)
s – a = \(\frac{53}{2}\) – 15 = \(\frac{53-30}{2}=\frac{23}{2}\)
s- b = \(\frac{53}{3}\) – 17 = \(\frac{53-34}{2}=\frac{19}{2}\)
s – c = \(\frac{53}{3}\) – 21 = \(\frac{53-42}{2}=\frac{11}{2}\)
త్రిభుజ వైశాల్యం (హెరాన్ సూత్రం) A = \(\sqrt{S(S-a)(S-b)(S-c)}\)
∴ A = \(\sqrt{\frac{53}{2}\left(\frac{23}{2}\right)\left(\frac{19}{2}\right)\left(\frac{11}{2}\right)}\)
A = \(\sqrt{\frac{53 \times 23 \times 19 \times 11}{16}}\)
A = \(\frac{1}{4} \sqrt{254771}\) చ.మీటర్లు.
![]()
ప్రశ్న 5.
బిందువులు (0, 0), (4, 0) మరియు (4, 3) లతో ఏర్పడు త్రిభుజ వైశాల్యంను హెరాన్ సూత్రం ద్వారా కనుగొనండి. (పేజీ నెం. 183)
సాధన.
A (0, 0), B (4, 0), C(4, 3)
a = BC = |y2 – y1| = |3 – 0| = 3 యూనిట్లు
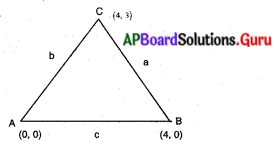
b = AC = \(\sqrt{x^{2}+y^{2}}\)
= \(\sqrt{4^{2}+(-3)^{2}}=\sqrt{16+9}\)
= √25 = 5 యూనిట్లు
C = AB = |x2 – x1| = |4| = 4 యూ.
S = \(\frac{a+b+c}{2}=\frac{3+4+5}{2}\) = 6
∴ త్రిభుజ వైశాల్యం (హెరాన్ సూత్రం)
A = \(\sqrt{s(s-a)(s-b)(s-c)}\)
= \(\sqrt{6(6-3)(6-5)(6-4)}\)
= \(\sqrt{6 \times 3 \times 1 \times 2}=\sqrt{36}\) = 6 చ.యూ.
∴ త్రిభుజ వైశాల్యం = 6 చ. యూనిట్లు.
సరిచూచుకొవడం :
3, 4, 5 భుజాలుగా గల త్రిభుజం లంబకోణ త్రిభుజం అవుతుంది.
∴ లంబకోణ త్రిభుజ వైశాల్యం = \(\frac{1}{2}\) × 3 × 4 = 6 చ. యూనిట్లు.
![]()
ప్రయత్నించండి:
ప్రశ్న 1.
ఏదేని ఒక బిందువు Aను X-అక్షంపై, మరొక బిందువు Bను Y- అక్షంపై తీసుకొని AOB త్రిభుజ వైశాల్యం కనుగొనండి. మీ మిత్రులు చేసిన వాటిని గమనించండి. మీరేం గమనించారు ? (పేజీ నెం. 178)
సాధన.
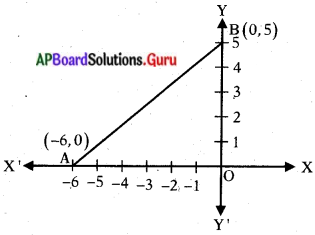
A(- 6, 0), B(0, 5) బిందువులు తీసుకొందాం.
∆AOB ఒక లంబకోణ త్రిభుజం అవుతుంది.
∆AOB యొక్క భూమి OA = 6 యూనిట్లు
ఎత్తు OA = 5 యూనిట్లు
∆AOB వైశాల్యం = \(\frac{1}{2}\) × భూమి × ఎత్తు
= \(\frac{1}{2}\) × 6 × 5 = 15 చ.యూ.
గమనించిన అంశాలు :
(i) X – అక్షంపై ఒక బిందువు, Y – అక్షంపై మరొకmబిందువు గల త్రిభుజం లంబకోణ – త్రిభుజం అవుతుంది.
(ii) బిందువులలోని x, y నిరూపకాలు ఒకటి భూమి, మరొకటి ఎత్తు అవుతుంది.
(iii) ఏర్పడు త్రిభుజం’ యొక్క వైశాల్యము x, y ల లబ్దంలో సగం ఉంటుంది.
(x1 , 0) మరియు (0, y1) మరియు నిరూపక అక్షాలతో ఏర్పడే త్రిభుజ వైశాల్యం
A = \(\frac{1}{2}\) |x1 y1| చ.యూనిట్లు.
![]()
ప్రశ్న 2.
బిందువులు (0, – 1), (2, 1) (0, 3) మరియు (- 2, 1) లు శీర్షాలుగా గల చతురస్రము యొక్క వైశాల్యము కనుగొనండి. (పేజీ నెం. 181)
సాధన.

ABCD చతురస్రాన్ని కర్ణం AC, ∆ABC మరియు ∆ADC అనే త్రిభుజాలుగా విభజిస్తుంది.
∴ ∆ABCవైశాల్యం = \(\frac{1}{2}\) |x1(y2 – y3) + x2 (y3 – y1) + x3 (y1 – y2)|
= \(\frac{1}{2}\) |0 (1 – 3) + 2 [3 – (- 1)] + 0(- 1 – 1)|
= \(\frac{1}{2}\) |0 + 8 + 0|
= \(\frac{1}{2}\) |8| = 4 చ. యూనిట్లు,
∴ ∆ABC వైశాల్యం = 4 చ. యూనిట్లు.
∆ADC వైశాల్యం = \(\frac{1}{2}\) |0(1 – 3) + (- 2) [ 3 – (- 1)] +0 (- 1 – 1)|
= \(\frac{1}{2}\) × 8 = 4 చ.యూ.
∆ADC వైశాల్యం = 4 చ.యూ.
చతురస్రం ABCD వైశాల్యం = 2 ∆ABC వైశాల్యం + ∆ADC వైశాల్యం
= 4 + 4 = 8 చ. యూనిట్లు
రెండవ పద్ధతి :
ABCD చతురస్రాన్ని కర్ణం AC రెండు సర్వసమాన త్రిభుజాలు ∆ABC మరియు ∆ADCలుగా విభజిస్తుంది.
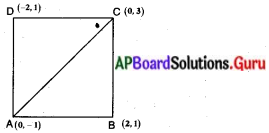
∆ABC వైశాల్యం = ∆ADC వైశాల్యం
చతురస్రం ABCD వైశాల్యం = 2 × ∆ABC వైశాల్యం
= 2 × \(\frac{1}{2}\) |0(1 – 3) +2[3 – (- 1)] + 0(- 1 – 1)|
= \(\frac{1}{2}\) |0 + 2 (4) + 0|
= | 8| = 8 చ. యూనిట్లు
∴ ABCD చతుర్భుజ వైశాల్యం = 8 చ. యూనిట్లు
మూడవ పద్ధతి :
చతురస్రం ABCD యొక్క ఒక భుజం AB = \(\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)
= \(\sqrt{(2-0)^{2}+\left[(1-(-1))^{2}\right]}\)
= \(\sqrt{2^{2}+2^{2}}=\sqrt{4+4}\)
భుజం AB = √8 యూనిట్లు.
చతురస్ర వైశాల్యం = భుజం × భుజం
= √ 8 × √8 = 8 చ.యూనిట్లు.
నాలుగవ పద్ధతి :
కర్ణం AC పొడవు d = |y2 – y1|
= |3 – (- 1)| = |4| = 4 యూ.
చతురస్ర వైశాల్యం A = \(\frac{\mathrm{d}^{2}}{2}=\frac{4^{2}}{2}\)
= \(\frac{16}{2}\) = 8 చ.యూనిట్లు.
![]()
ఆలోచించి, చర్చించి, రాయండి:
ప్రశ్న 1.
బిందువులు A(x1, y1), B(x2, y2), C(x3, y3) నిరూపకతలంపై ఉన్నవనుకొనుము. అయిన కింది త్రిభుజాల యొక్క వైశాల్యమును కనుగొనండి. మరియు వాటి వైశాల్యముల గురించి గ్రూపులలో మీ స్నేహితులతో చర్చించండి. (పేజీ నెం. 178)
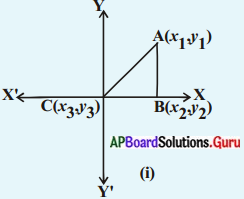
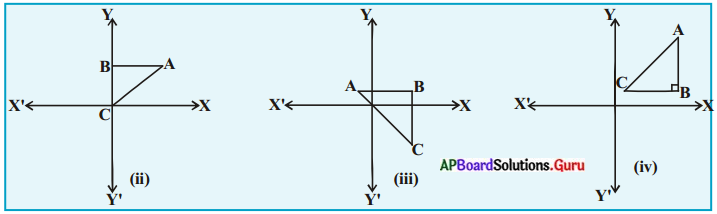
సాధన.
(i) 1వ పటం నుండి : –
A(x1, y1), B(x2, y2), C(x3, y3) = (0, 0)
ABC ఒక లంబకోణ త్రిభుజము,
∴ ∆ABC వైశాల్యం = \(\frac{1}{2}\) భూమి × ఎత్తు
= \(\frac{1}{2}\) BC × AB
= \(\frac{1}{2}\) |x2 (y1 – y2) | చ.యూ.
గమనిక : వైశాల్యము ధనాత్మకము కావున పరమ మూల్యం | | ను తీసుకొంటాము. ..
(ii) 2వ పటం నుండి :
భూమి BC = ya
ఎత్తు AB = x1 – x2
∆ABC వైశాల్యం = \(\frac{1}{2}\) BC × AB
= \(\frac{1}{2}\) |y2 (x2 – x1)| చ.యూ.
![]()
(iii) 3వ పటం నుండి :
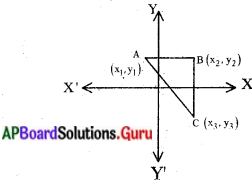
∆ABC వైశాల్యం = \(\frac{1}{2}\) AB × BC
= \(\frac{1}{2}\) |(x2 – x1) (y2 – y3) చ.యూ.
(iv) 4 వ పటం నుండి :
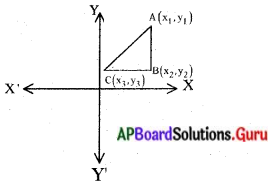
∴ ∆ABC వైశాల్యం – – BC X AB
= \(\frac{1}{2}\) |(x2 – x3) (y1 – y2)|
గమనిక :
X, Y అక్షాలకు సమాంతరంగా భుజాలు గల త్రిభుజం యొక్క వైశాల్యము X నిరూపకాల భేదం మరియు y నిరూపకాల భేదాల లబ్దానికి సమానము. మరియు ఏర్పడే త్రిభుజము ‘ లంబకోణ త్రిభుజము అవుతుంది.
![]()
ప్రశ్న 2.
కింది. బిందువులతో ఏర్పడే త్రిభుజ వైశాల్యాన్ని కనుగొనండి. (పేజీ నెం. 181)
(i) (2, 0), (1, 2), (1, 6)
(ii) (3, 1), (5, 0), (1, 2)
(iii) (- 1.5, 3), (6, 2), (- 3, 4)
(a) మీరేం గమనించారు ?
(b) ఈ బిందువులను మూడు వేర్వేరు గ్రాఫులలో గుర్తించండి. మీరేం గమనించారు ? మీ మిత్రునితో చర్చించండి.
(c) వైశాల్యం ‘0’ (సున్నా) చ.యూనిట్లు గల త్రిభుజమును గీయగలమా ? మరి దీని అర్థమేమిటి ?
(i) (2, 0), (1, 2), (1, 6)
సాధన.
మూడవ బిందువు (- 1, 6) గా తీసుకొందాం.
(2, 0), (1, 2), (-1, 6) బిందువులు శీర్షాలుగా గల త్రిభుజ వైశాల్యం A = \(\frac{1}{2}\) |x1 (y2 – y33) + x2 (y3 – y1) + x3 (y1 – y2)|
= \(\frac{1}{2}\) |2(2 – 6) + 1(6 – 0) + (- 1)(0 – 2)|
= \(\frac{1}{2}\) (2(- 4) + 6 – 1(- 2)|
= \(\frac{1}{2}\) |- 8 + 6 + 2|
= \(\frac{1}{2}\) |0| = 0.
త్రిభుజ వైశాల్యం = 0 చ. యూనిట్లు.
(ii) (3, 1), (5, 0), (1, 2)
సాధన.
∆ = \(\frac{1}{2}\) |3(0 – 2) + 5(2 – 1) + 1(1 – 0)|
= \(\frac{1}{2}\) |- 6 + 5 + 1| = 0
త్రిభుజ వైశాల్యం = 0 చ. యూనిట్లు.
![]()
(iii) (- 1.5, 3), (6, 2), (- 3, 4)
సాధన.
రెండవ బిందువు (6, – 2) గా తీసుకొందాం.
(- 1.5, 3), (6, – 2) మరియు (- 3, 4)
బిందువులు శీర్షాలుగా గల త్రిభుజ వైశాల్యం, = \(\frac{1}{2}\) |(- 1.5) [- 2 – 4] + 6 (4 – 3) + (- 3) [3 – (- 2)]|
= \(\frac{1}{2}\) |(- 1.5) (- 6) + 6 (1) – 3 (5)|
= \(\frac{1}{2}\) |9 + 6 – 15|
= \(\frac{1}{2}\) |15 – 15| = \(\frac{1}{2}\) |0| = 0
(a) పై మూడు సందర్భాలలోనూ త్రిభుజం యొక్క వైశాల్యము శూన్యము అనగా ఇచ్చిన బిందువులు శీర్షాలుగా గల త్రిభుజం ఏర్పడదు అని తెలుస్తున్నది. కావున మూడు సందర్భాలలోను ఇచ్చిన మూడు బిందువులు ఒకే రేఖపై ఉంటాయి. అనగా ఆ మూడు బిందువులు సరేఖీయాలు అవుతాయి. కాబట్టి వైశాల్యము ‘0’ (సున్నా) చ.యూనిట్లు గల త్రిభుజాన్ని గీయలేము. త్రిభుజ వైశాల్య సూత్రం = 0 చ. యూనిట్లు.
∆ ABC వైశాల్యం సున్న ⇒ A, B, C లు సరేఖీయాలు.
(b) ఈ బిందువులను మూడు వేర్వేరు గ్రాఫులలో గుర్తించండి. మీరేం గమనించారు? మీ మిత్రులతో చర్చించండి. (పేజీ నెం. 181)
సాధన.
(2, 0), (1, 2), (- 1, 6), (3, 1), (5, 0), (1, 2), (- 1.5, 3), (6, – 2), (- 3, 4) లను గ్రాఫ్ పై గుర్తించుట.
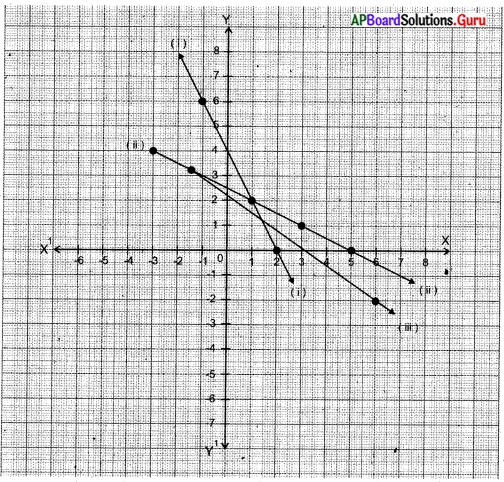
కావున ఇచ్చిన బిందువులు సరేఖీయాలు.
(c) వైశాల్యం )(సున్నా). చ.యూనిట్లు గల త్రిభుజమును గీయగలమా ? మరి దీని అర్థమేమిటి ? (పేజీ నెం. 181)
సాధన.
వైశాల్యం 0 చ.యూ, గల త్రిభుజాన్ని నిర్మించలేము. దీని అర్థం ఇచ్చిన బిందువులు సరేఖీయాలు అనగా ఒకే సరళరేఖ పై గల బిందువులు
![]()
ఇవి చేయండి:
కిందనీయబడిన బిందువులను నిరూపకతలంపై గుర్తించి వాటిని కలుపుము.
(పేజీ నెం. 185)
(i) A(1, 2), B(- 3, 4) మరియు C(7,- 1)
(ii) P(3, – 5), Q(5, – 1), R(2, 1) మరియు S(1, 2) ఇందులో ఏది సరళరేఖను సూచిస్తుంది ? ఏది సూచించదు ? ఎందుకు?
సాధన.
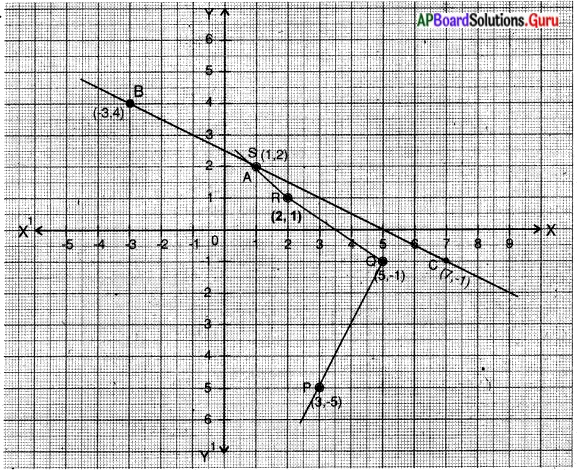
(i) వ సమస్యలోని బిందువులు A, B, C లు – శేఖను సూచిస్తాయి.
(ii) వ సమస్యలోని బిందువులు P, Q, R, S లు సరళరేఖను సూచించవు.
ఎందుకనగా A, B, C లు సరేఖీయ బిందువులు. కాబట్టి ఒకే సరళరేఖపై ఉంటాయి. P, Q, R, S లు సరేఖీయాలు కావు. కావున ఒకే సరళరేఖపై ఉండవు.
కింది బిందువులతో ఏర్పడు రేఖాఖండము \(\overline{\mathbf{A B}}\) వాలును కనుగొనండి. (పేజీ నెం. 188)
(i) A(4, -6) మరియు B (7, 2)
సాధన.
\(\overline{\mathbf{A B}}\) వాలు, m =\(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)
= \(\frac{2-(-6)}{7-4}\)
= \(\frac{2+6}{3}\) = \(\frac{8}{3}\).
![]()
(ii) A(8, – 4) మరియు B (-4, 8)
సాధన.
AB వాలు, m = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)
= \(\frac{8-(-6)}{-4-8}\)
= \(\frac{12}{-12}\) = – 1
(iii) A(- 2, – 5) మరియు B(1, – 7) .
సాధన.
AB వాలు, m = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)
= \(\frac{-7-(-5)}{1-(-2)}=\frac{-7+5}{1+2}=\frac{-2}{3}\)
![]()
ప్రయత్నించండి:
కింద ఇవ్వబడిన బిందువులు \(\overline{\mathbf{A B}}\) రేఖపై ఉన్నవి. \(\overline{\mathbf{A B}}\) రేఖ వాలు. కనుగొనండి. (పేజీ నెం. 188)
ప్రశ్న 1.
A(2, 1) మరియు B(2, 6)
సాధన.
\(\overline{\mathbf{A B}}\) వాలు, m = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)
= \(\frac{6-1}{2-2}=\frac{6}{0}\) నిర్వచించబడదు.
ప్రశ్న 2.
A(- 4, 2) మరియు B (- 4, – 2)
\(\overline{\mathbf{A B}}\) వాలు, m = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)
= \(\frac{-2-2}{-4-(-4)}\)
= \(\frac{-4}{-4+4}=\frac{4}{0}\) నిర్వచించబడదు.
ప్రశ్న 3.
A(- 2, 8) మరియు B (- 2, – 2)
సాధన.
\(\overline{\mathbf{A B}}\) వాలు, m = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)
= \(=\frac{-2-8}{-2+2}\)
= \(\frac{-10}{0}\) నిర్వచించబడదు.
∴ వాలు నిర్వచింపబడదు.
![]()
ప్రశ్న 4.
“ఇచ్చిన బిందువులతో ఏర్పడు \(\overline{\mathbf{A B}}\) రేఖాఖండం Y-అక్షానికి సమాంతరంగా ఉంటుంది”. ఈ వాక్యము సరైనదేనా ? ఎందుకు ? అయితే వాలు ఏ విధంగా ఉంటుంది? (పేజీ నెం. 188)
సాధన.
“ఇచ్చిన బిందువులతో ఏర్పడు \(\overline{\mathbf{A B}}\) రేఖండము Y – అక్షానికి సమాంతరంగా ఉంటుంది” అనే ఈ వాక్యము సరైనదే. ఎందుకనగా ఇచ్చిన రెండు బిందువులలోని X నిరూపకాలు సమానంగా కలవు. అనగా ఇచ్చిన రెండు బిందువులు (x1, y1) మరియు (x2, y2) రూపంలో ఉన్నాయి. Y – అక్షానికి సమాంతరంగా గల రేఖల యొక్క వాలు నిర్వహించబడదు.
ఆలోచించి, చర్చించి, రాయండి:
ప్రశ్న 1.
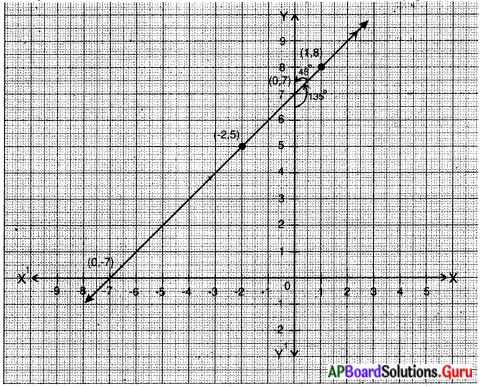
y = x + 7 సమీకరణం ఒక సరళరేఖను సూచిస్తుందా? నిరూపకతలంలో గీసి చూడండి. ఈ సరళరేఖ X – అక్షాన్ని ఏ బిందువు వద్ద ఖండిస్తుంది? అదే విధంగా ఈ సరళరేఖ Y – అక్షంతో ఎంత కోణం చేస్తుంది ? మీ మిత్రులతో … చర్చించండి. : (పేజీ నెం. 185)
సాధన.
y = x + 7

y = x + 7 సూచించు సరళరేఖ X – అక్షాన్ని (0, – 7) బిందువు వద్ద ఖండిస్తుంది. మరియు ఈ సరళరేఖ 1 0 | y = 0 + 7 = 7 | (0, 7) .
Y- అక్షంతో ధనదిశలో 135° కోణాన్ని, రుణదిశలో 45° కోణాన్ని చేస్తుంది.
y= x + 7 గ్రాఫ్ :
ప్రశ్న 2.
బిందువులు A(3, 2), B (- 8, 2) లు \(\overline{\mathbf{A B}}\) రేఖపై ఉన్నచో ఆ రేఖ వాలును కనుగొనండి. \(\overline{\mathbf{A B}}\) రేఖ ఎప్పుడు X-అక్షమునకు సమాంతరంగా ఉంటుంది ? ఎందుకు ? మీ స్నేహితులతో గ్రూపులలో చర్చించండి. (పేజీ నెం. 188)
సాధన.
బిందువులు = A (3, 2), B (- 8, 2) అయిన \(\overline{\mathbf{A B}}\) రేఖవాలు (m) = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)
= \(\frac{2-2}{-8-3}=\frac{0}{-11}\) = 0
A, B బిందువులలో Y నిరూపకాలు సమానంగా ఉన్నప్పుడు \(\overline{\mathbf{A B}}\) రేఖ X – అక్షానికి సమాంతరంగా ఉంటుంది. ఈ సందర్భంలో \(\overline{\mathbf{A B}}\) రేఖ వాలు ‘0’, అనగా ఒక రేఖ వాలు ‘0’ (సున్న) అయితే ఆ రేఖ X – అక్షానికి సమాంతరంగా ఉంటుంది.
![]()
ఉదాహరణలు:
ప్రశ్న 1.
A (4, 0) మరియు B (8, 0) బిందువుల మధ్య దూరం ఎంత ? (పేజీ నెం. 162)
సాధన.
A, B లలో y – నిరూపకాలు సమానం.
A, B ల మధ్య దూరం = |x2 – x1|
= |8 – 4| = 4 యూనిట్లు.
ప్రశ్న 2.
A మరియు B బిందువులు వరుసగా (8, 3), ( – 4, 3), అయిన వాటి మధ్యదూరాన్ని కనుక్కోండి. (పేజీ నెం. 162)
సాధన.
A (8, 3), B (- 4, 3), బిందువులలో y నిరూపకాలు సమానం.
A, B ల మధ్య దూరం = |x2 – x1|
. = |- 4 – 8|
= |- 12| = 12 యూనిట్లు.
![]()
ప్రశ్న 3.
బిందువులు A(4, 3) మరియు B(8, 6)ల మధ్యదూరాన్ని కనుగొనండి. (పేజీ నెం. 164)
సాధన.
A (4, 3), B (8, 6) (x1, y1), (x2, y2) లతో పోల్చగా x1 = 4, x2 = 8, y1 = 3, y2 = 6
∴ AB ల మధ్య దూరం = d = \(\sqrt{\left(\mathrm{x}_{2}-\mathrm{x}_{1}\right)^{2}+\left(\mathrm{y}_{2}-\mathrm{y}_{1}\right)^{2}}\)
= \(\sqrt{(8-4)^{2}+(6-3)^{2}}=\sqrt{4^{2}+3^{2}}\)
= \(\sqrt{16+9}=\sqrt{25}\) = 5 యూనిట్లు.
ప్రశ్న 4.
బిందువులు A (4, 2), B (7, 5) మరియు C(9, 7) లు ఒకే సరళరేఖపై ఉన్నాయని చూపండి. (పేజీ నెం. 164)
సాధన.
ఇచ్చిన బిందువులు A (4, 2), B (7, 5), C (9, 7) AB, BC, AC లను కనుగొందాము.
బిందువుల మధ్య దూరం = \(\sqrt{\left(\mathrm{x}_{2}-\mathrm{x}_{1}\right)^{2}+\left(\mathrm{y}_{2}-\mathrm{y}_{1}\right)^{2}}\)
AB = d = \(\sqrt{(7-4)^{2}+(5-2)^{2}}\)
= \(\sqrt{3^{2}+3^{2}}=\sqrt{9+9}=\sqrt{18}\)
= \(\sqrt{9 \times 2}=3 \sqrt{2}\)
BC = \(\sqrt{(9-7)^{2}+(7-5)^{2}}\)
= \(\sqrt{2^{2}+2^{2}}=\sqrt{4+4}=\sqrt{4 \times 2}=2 \sqrt{2}\)
AC = \(\sqrt{(9-4)^{2}+(7-2)^{2}}\)
= \(\sqrt{5^{2}+5^{2}}=\sqrt{25+25}=\sqrt{50}\)
= \(\sqrt{25 \times 2}\) = 5√2
AB + BC = 3√2 + 2√2 = 5√2 = AC.
∴ AB + BC = AC.
కావున A(4, 2), B(7, 5) మరియు C(9, 7)లు ఒకే సరళరేఖపై ఉన్నాయి.
![]()
ప్రశ్న 5.
బిందువులు (3, 2), (- 2, – 3) మరియు (2, 3)లు త్రిభుజాన్ని ఏర్పరుస్తాయా ? (పేజీ నెం. 165)
సాధన.
ఇచ్చిన బిందువులు A(3, 2), B(- 2, – 3), C(2, 3) AB, BC, AC లను కనుగొందాము.
AB = \(\sqrt{(-2-3)^{2}+(-3-2)^{2}}\)
= \(\sqrt{(-5)^{2}+(-5)^{2}}\)
= \(\sqrt{25+25}=\sqrt{50}\)
= 7.07 యూనిట్లు (సుమారుగా)
BC = \(\sqrt{[2-(-2)]^{2}+[3-(-3)]^{2}}\)
= \(\sqrt{4^{2}+6^{2}}=\sqrt{16+36}\)
= √52 = 7.21 యూనిట్లు (సుమారుగా)
AC = \(\sqrt{(2-3)^{2}+(3-2)^{2}}\)
= \(\sqrt{(-1)^{2}+(1)^{2}}=\sqrt{2}\)` `
= 1.41 యూనిట్లు (సుమారుగా)
పై విలువలను బట్టి ఏ రెండు విలువల మొత్తమైనా మూడవ దాని కంటే ఎక్కువ. (త్రిభుజ అసమానత్వ నియమం ప్రకారం త్రిభుజంలో ఏవైనా రెండు భుజాల పొడవుల మొత్తం మూడవదాని కంటే ఎక్కువ) కావున బిందువులు A, B మరియు C లు ఒక విషమబాహు త్రిభుజాన్ని ఏర్పరుస్తాయి.
`(లేదా)
AB, BC, ACలలో ఏ రెండు రేఖాఖండాల మొత్తమైనా మూడవ దానికి సమానం కాలేదు. అనగా A, B, C లు సరేఖీయాలు కావు. కావున A, B, Cలు త్రిభుజాన్ని ఏర్పరుస్తాయి.
ప్రశ్న 6.
బిందువులు (1, 7), (4, 2), (- 1, – 1) మరియు (- 4, 4) లు ఒక చతురస్రం యొక్క శీర్షాలు అవుతాయని చూపండి. (పేజీ నెం. 165)
సాధన.
ఇచ్చిన బిందువులు A (1, 7), B (4, 2), C (-1, -1)
రెండు బిందువుల మధ్య దూరం d = \(\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)
AB = d = \(\sqrt{(4-1)^{2}+(2-4)^{2}}\)
= \(\sqrt{9+25}=\sqrt{34}\) యూనిట్లు
BC = \(\sqrt{(-1-4)^{2}+(-1-2)^{2}}\)
= \(\sqrt{25+9}=\sqrt{34}\) యూనిట్లు
CD = \(\sqrt{(-4-(-1))^{2}+(-4-(-1))^{2}}\)
= \(\sqrt{9+25}=\sqrt{34}\) యూనిట్లు
DA = \(\sqrt{(-4-1)^{2}+(4-7)^{2}}\)
= \(\sqrt{25+9}=\sqrt{34}\) యూనిట్లు
మరియు కర్ణాలు
AC = \(\sqrt{(-1-1)^{2}+(-1-7)^{2}}\)
= \(\sqrt{4+64}=\sqrt{68}\) యూనిట్లు
BD = \(\sqrt{(-4-4)^{2}+(4-2)^{2}}\)
= \(\sqrt{64+4}=\sqrt{68}\) యూనిట్లు
AB = BC = CD = DA మరియు AC = BD. నాలుగు భుజాలు సమానము మరియు కర్ణాలు సమానం.
∴ ABCD ఒక చతురస్రం అవుతుంది.
![]()
ప్రశ్న 7.
ప్రక్క పటం ఒక తరగతి గదిలోని డెస్క్ల యొక్క అమరికను చూపిస్తుంది. మాధురి, మీన, పల్లవిలు వరుసగా A (3, 1), B(6, 4) మరియు C(8, 6) స్థానాలలో కూర్చున్నారు. వారు ముగ్గురూ ఒకే సరళరేఖలో కూర్చున్నారని మీరు భావిస్తున్నారా ? మీ సమాధానానికి సరైన కారణం తెలపండి. (పేజీ నెం. 166)
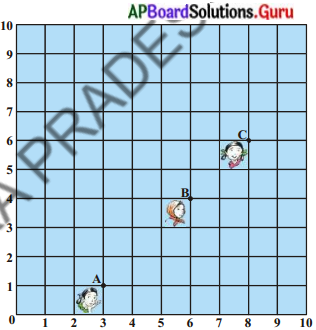
సాధన.
A(3, 1), B(6, 4), C (8, 6)
రెండు బిందువుల మధ్య దూరం \(\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}\)
AB = \(\sqrt{(6-3)^{2}+(4-1)^{2}}\)
= \(\sqrt{9+9}=\sqrt{9 \times 2}=3 \sqrt{2}\) యూనిట్లు
BC = \(\sqrt{(8-6)^{2}+(6-4)^{2}}\)
= \(\sqrt{4+4}=\sqrt{4 \times 2}=2 \sqrt{2}\) యూనిట్లు
AC = \(\sqrt{(8-3)^{2}+(6-1)^{2}}\)
= \(\sqrt{25+25}=\sqrt{25 \times 2}=\dot{5} \sqrt{2}\) యూనిట్లు
దీని నుండి ∴ AB + BC = 3√2 + 2√2 = 5√2 = AC
కాబట్టి A, B, C బిందువులు సరేఖీయాలు. కాబట్టి వారు ముగ్గురూ ఒకే సరళరేఖలో కూర్చున్నారు.
ప్రశ్న 8.
బిందువు (x, y) అనునది బిందువులు (7, 1) మరియు (3, 5) లకు – సమాన దూరంలో ఉన్నది. అయిన X మరియు y ల మధ్య సంబంధమును కనుగొనండి. (పేజీ నెం. 166).
సాధన.
P(x, y) బిందువు, A (7, 1) మరియు B (3, 5) లకు సమానదూరంలో ఉన్నది.
∴ AP = BP
⇒ AP2 = BP2
AP = \(\sqrt{(7-x)^{2}+(1-y)^{2}}\)
⇒ AP2 = (7 – x)2 + (1 – y)2
BP = \(\sqrt{(3-x)^{2}+(5-y)^{2}}\)
⇒ BP2 = (3 – x)2 + (5 – y)2
(7 – x)2 + (1 – y)2 = (3 – x)2 + (5 –2y)2
= 49 – 14x + x2 + 1 – 2y + y2
= 9 – 6x + x2 + 25 – 10y + y2
x2 + y2 – 14x – 2y + 50 – x2 – y2 + 6x + 10y – 34 = 0
– 8x + 8y + 16 = 0
– 8 [x – y – 2] = 0
∴ x – y – 2 = 0
కావలసిన సంబంధము x – y = 2.
![]()
ప్రశ్న 9.
A(6, 5) మరియు B(- 4, 3) లకు సమానదూరంలో Y-అక్షంపై ఉన్న బిందువు నిరూపకాలు కనుగొనండి. (పేజీ నెం. 167)
సాధన.
Y-అక్షంపై గల బిందువు (0, y) రూపంలో ఉంటుంది.
∴ A (6, 5) మరియు B (- 4, 3) బిందువులకు సమాన దూరంలో Y-అక్షంపై నున్న బిందువు P(0, y) అనుకొందాము.
PA = \(\sqrt{(6-0)^{2}+(5-y)^{2}}\)
= \(\sqrt{36+25-10 y+y^{2}}\)
= \(\sqrt{y^{2}-10 y+61}\)
PA2 = y2 – 10y + 61
PB = \(\sqrt{(-4-0)^{2}+(3-y)^{2}}\)
= \(\sqrt{16+9-6 y+y^{2}}\)
= \(\sqrt{y^{2}-6 y+25}\)
PB2 = y2 – 6y + 25
PA = PB
⇒ PA2 = PB2
y2 – 10y + 61 = y2 – 6y + 25
y2 – 10y + 61 – y2 + 6y – 25 = 0
– 4y + 36 = 0
4y = 36
∴ y = \(\frac{36}{4}\) = 9
∴ కావలసిన బిందువు P (0, y) = (0, 9).
సరిచూచుట :
AP = \(\sqrt{(6-0)^{2}+.(5-9)^{2}}\)
= \(\sqrt{36+16}=\sqrt{52}\)
BP = \(\sqrt{(-4-0)^{2}+(3-9)^{2}}\)
= \(\sqrt{16+36}=\sqrt{52}\)
ప్రశ్న 10.
బిందువులు (4, – 3) మరియు (8, 5) లచే ఏర్పడు. రేఖాఖండమును 3 : 1 నిష్పత్తిలో అంతరంగా విభజించు బిందువు నిరూపకాలను కనుగొనండి. (పేజీ నెం. 171)
సాధన.
ఇచ్చిన బిందువులు (4, -3) మరియు (8, 5) లను P (x, y) 3 : 1 నిష్పత్తిలో విభిజిస్తుంది అనుకొనుము.
విభజన సూత్రం P(x, y) = \(\left(\frac{\mathrm{m}_{1} \mathrm{x}_{2}+\mathrm{m}_{2} \mathrm{x}_{1}}{\mathrm{~m}_{1}+\mathrm{m}_{2}}, \frac{\mathrm{m}_{1} \mathrm{y}_{2}+\mathrm{m}_{2} \mathrm{y}_{1}}{\mathrm{~m}_{1}+\mathrm{m}_{2}}\right)\)
= \(\left(\frac{3(8)+1(4)}{3+1}, \frac{3(5)+1(-3)}{3+1}\right)\)
= \(\left(\frac{24+4}{4}, \frac{15-3}{4}\right)=\left(\frac{28}{4}, \frac{12}{4}\right)\)
∴ కావలసిన బిందువు P(x, y) = (7, 3).
![]()
ప్రశ్న 11.
బిందువులు (3, 0) మరియు (-1, 4) లచే ఏర్పడు – రేఖాఖండం యొక్క మధ్యబిందువును కనుగొనండి. (పేజీ నెం. 171)
సాధన.
బిందువులు (3, 0) మరియు (- 1, 4) లచే ఏర్పడు రేఖాఖండం యొక్క మధ్యబిందువు M(x, y) అనుకొనిన,
మధ్యబిందువు M(x, y) = \(\left(\frac{x_{1}+x_{2}}{2}, \frac{y_{1}+y_{2}}{2}\right)\)
M(x, y) = \(\left(\frac{3+(-1)}{2}, \frac{0+4}{2}\right)\)
= \(\left(\frac{2}{2}, \frac{4}{2}\right)\) = (1, 2).
ప్రశ్న 12.
బిందువులు (3, – 5), (- 7, 4), (10, – 2) లు శీర్షాలుగా గల త్రిభుజం యొక్క గురుత్వ కేంద్రంను కనుగొనండి. (పేజీ నెం. 173) .
సాధన.
ఇచ్చిన బిందువులు (3, – 5), (- 7, 4), (10, – 2).
గురుత్వ కేంద్రం నిరూపకాలు = \(\left(\frac{x_{1}+x_{2}+x_{3}}{3}, \frac{y_{1}+y_{2}+y_{3}}{3}\right)\)
= \(\left(\frac{3+(-7)+10}{3}, \frac{(-5)+4+(-2)}{3}\right)\)
= \(\left(\frac{6}{3}, \frac{-3}{3}\right)\) = (2, – 1)
∴ గురుత్వ కేంద్రం = (2, – 1).
![]()
ప్రశ్న 13.
బిందువులు AC- 6, 10) మరియు B (3, – 8) లచే ఏర్పడు రేఖాఖండమును బిందువు (-4, 6) ఏ నిష్పత్తిలో విభజిస్తుంది ? (పేజీ నెం. 173)
సాధన.
A(- 6, 10), B(3, – 8) రేఖాఖండాన్ని (- 4, 6) అంతరంగా m1 : m2 నిష్పత్తిలో విభజిస్తుందనుకొనిన
(- 4, 6) = \(\left(\frac{3 m_{1}-6 m_{2}}{m_{1}+m_{2}}, \frac{-8 m_{1}+10 m_{2}}{m_{1}+m_{2}}\right)\)
(x, y) = (a, b) ⇒ x = a మరియు y = b అని మనకు తెలుసు.
∴ – 4 = \(\frac{3 m_{1}-6 m_{2}}{m_{1}+m_{2}}\) ………. (1) మరియు
6 = \(\frac{-8 m_{1}+10 m_{2}}{m_{1}+m_{2}}\) ……….. (2)
(1) ⇒ – 4m1 – 4m2 = 3m1 – 6m2
– 4m1 – 3m1 = – m2 + 4m2
– 7m1 = – 2m2
7m1 = 2m2
∴ \(\frac{\mathrm{m}_{1}}{\mathrm{~m}_{2}}=\frac{2}{7}\)
అనగా m1 : m2 = 2 : 7
ఈ నిష్పత్తి (2) సమీకరణాన్ని కూడా సంతృప్తిపరుస్తుందని చూపవచ్చును.
(2) ⇒ 6 = 
∴ 6 = 6 కావున బిందువులు A (-6, 10) మరియు B (3, – 8) లచే ఏర్పడు రేఖాఖండమును (- 4, 6) బిందువు 2 : 7 నిష్పత్తిలో విభజిస్తుంది.
ప్రశ్న 14.
బిందువులు A(2, – 2) మరియు B(- 7, 4) లచే, ఏర్పడు రేఖాఖండము యొక్క ప్రాథాకరణ బిందువులు కనుగొనండి. (పేజీ నెం. 175)
సాధన.
AB రేఖాఖండం యొక్క త్రిథాకరణ బిందువులు P మరియు Q లు అనుకొనిన AP = PQ = QB (పటంలో చూపినట్లు).
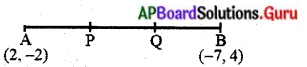
అందువల్ల AB రేఖాఖండాన్ని బిందువు P అంతరంగా 1 : 2 నిష్పత్తిలో విభజిస్తుంది. కావున విభజన సూత్రం నుండి.
P (x, y) = \(\left(\frac{m_{1} x_{2}+m_{2} x_{1}}{m_{1}+m_{2}}, \frac{m_{1} y_{2}+m_{2} y_{1}}{m_{1}+m_{2}}\right)\)
= \(\left(\frac{1(-7)+2(2)}{1+2}, \frac{1(4)+2(-2)}{1+2}\right)\)
= \(\left(\frac{-7+4}{3}, \frac{4-4}{3}\right)=\left(\frac{-3}{3}, \frac{0}{3}\right)\) = (- 1, 0)
ఇపుడు బిందువు Q కూడా AB రేఖాఖండాన్ని అంతరంగా 2 : 1 నిష్పత్తిలో విభజిస్తుంది.
అందువల్ల బిందువు Q యొక్క నిరూపకాలు = \(\left(\frac{2(-7)+1(2)}{2+1}, \frac{2(4)+1(-2)}{2+1}\right)\)
అనగా \(\left(\frac{-14+2}{3}, \frac{8-2}{3}\right)\)
= \(\left(\frac{-12}{3}, \frac{6}{3}\right)\) = (- 4, 2)
కాబట్టి, AB రేఖాఖండము యొక్క ప్రాథాకరణ బిందువులు P(- 1, 0) మరియు Q(- 4, 2).
![]()
ప్రశ్న 15.
బిందువులు (5, – 6) మరియు (- 1, – 4) లచే ఏర్పడు రేఖాఖండమును Y- అక్షము ఏ నిష్పత్తిలో విభజిస్తుంది? ఆ ఖండన బిందువును కనుగొనండి. (పేజీ నెం. 176)
సాధన.
బిందువులు A(5, – 6) మరియు B(- 1, – 4) లచే ఏర్పడు రేఖాఖండము AB ని Y – అక్షంపైనున్న బిందువు
P(0, y), m1 : m2 నిష్పత్తిలో విభజిస్తుందనుకొంటే
P(o, y) = \(\left(\frac{\mathrm{m}_{1}(-1)+\mathrm{m}_{2}(5)}{\mathrm{m}_{1}+\mathrm{m}_{2}}, \frac{\mathrm{m}_{1}(-4)+\mathrm{m}_{2}(-6)}{\mathrm{m}_{1}+\mathrm{m}_{2}}\right)\)
(0, y) = \(\left(\frac{-m_{1}+5 m_{2}}{m_{1}+m_{2}}, \frac{-4 m_{1}-6 m_{2}}{m_{1}+m_{2}}\right)\)
⇒ \(\frac{-\mathrm{m}_{1}+5 \mathrm{~m}_{2}}{\mathrm{~m}_{1}+\mathrm{m}_{2}}\) = 0
⇒ – m1 + 5m2 = 0
⇒ – m1 = – 5m2
⇒ m1 = 5m2
\(\frac{\mathrm{m}_{1}}{\mathrm{~m}_{2}}=\frac{5}{1}\)
Y- అక్షం విభజించే నిష్పత్తి = m1 : m2 = 5 : 1
ఇప్పుడు y = \(\frac{-4 m_{1}-6 m_{2}}{m_{1}+m_{2}}\)
⇒ \(\frac{-4 \frac{m_{1}}{m_{2}}-6}{\frac{m_{1}}{m_{2}}+1}=\frac{-4\left(\frac{5}{1}\right)-6}{\frac{5}{1}+1}=\frac{-20-6}{6}\)
⇒ y = \(\frac{-26}{6}\) = \(\frac{-13}{3}\)
∴ ఖండన బిందువు P = ( 0, \(\frac{-13}{3}\))
2వ పద్ధతి :
A(x1, y1), B (x2, y2) బిందువులను Y- అక్షం విభజించే నిష్పత్తి m1 : m2 = – x1 : x2
∴ (5, – 6) మరియు (-1, – 4) లను Y – అక్షం విభజించే నిష్పత్తి = – x1 : x2 = – 5 : – 1
= 5 : 1
(5, – 6) మరియు (- 1, – 4) లను 5 : 1 నిష్పత్తిలో విభజించే బిందువే ఖండన బిందువు అవుతుంది.
∴ ఖండన బిందువు = 
∴ ఖండన బిందువు P = (0, \(\frac{-13}{3}\))
3వ పద్ధతి :
పాఠ్యపుస్తకంలో కలదు చూడగలరు.
![]()
ప్రశ్న 16.
బిందువులు A(7, 3), B(6, 1), C(8, 2) మరియు D(9, 4)లు వరుసగా సమాంతర చతుర్భుజం యొక్క శీర్షాలని చూపండి. (పేజీ నెం. 176)
సాధన.
బిందువులు A(7, 3), B(6, 1), C(8, 2) మరియు D(9, 4) లు వరుసగా ఒక సమాంతర చతుర్భుజం శీర్షాలు అనుకొనిన, సమాంతర చతుర్భుజంలో కర్ణాలు పరస్పరం సమద్విఖండన చేసుకుంటాయని తెలుసు.
∴ అందువల్ల కర్ణాలు AC మరియు BD ల మధ్య బిందువులు సమానం కావాలి.
A (7, 3), C (8, 2) ల మధ్యబిందువు = \(\left(\frac{7+8}{2}, \frac{3+2}{2}\right)=\left(\frac{15}{2}, \frac{5}{2}\right)\)
B(6, 1), D(9, 4) ల మధ్య బిందువు = \(\left(\frac{6+9}{2}, \frac{1+4}{2}\right)=\left(\frac{15}{2}, \frac{5}{2}\right)\)
∴ AC మధ్య బిందువు = DB మధ్య బిందువు.
కాబట్టి బిందువులు A, B, C, D లు సమాంతర చతుర్భుజం యొక్క శీర్షాలు అవుతాయి.
ప్రశ్న 17.
బిందువులు A(6, 1), B (8, 2), C(9, 4) మరియు D(p, 3) లు వరుసగా సమాంతర చతుర్భుజం యొక్క శీర్షాలయిన p యొక్క విలువను కనుగొనండి. (పేజీ నెం. 177)
సాధన.
ఇచ్చిన బిందువులు A(6, 1), B(8, 2), C(9, 4) D(p, 3) సమాంతర చతుర్భుజంలో కర్ణాలు పరస్పరం సమద్విఖండన చేసుకుంటాయని మనకు తెలుసు.
కాబట్టి AC మధ్య బిందువు = BD మధ్య బిందువు
\(\left(\frac{6+9}{2}, \frac{1+4}{2}\right)=\left(\frac{8+\mathrm{p}}{2}, \frac{5}{2}\right)\)
⇒ \(\left(\frac{15}{2}, \frac{5}{2}\right)=\left(\frac{8+\mathrm{p}}{2}, \frac{5}{2}\right)\)
⇒ \(\frac{15}{2}=\frac{8+p}{2}\)
⇒ 15 = 8 + p
⇒ P = 15 – 8 =7
∴ p = 7.
![]()
ప్రశ్న 18.
బిందువులు A(1, – 1), B (- 4, 6), C(- 3, – 5)లు శీర్షాలుగా గల త్రిభుజ యొక్క వైశాల్యం కనుగొనండి..
సాధన.
A(1, – 1), B (- 4, 6), C(- 3, – 5) లు శీర్షాలుగా గల త్రిభుజ వైశాల్యం = \(\frac{1}{2}\) |x1 (y2 – y3) + x2 (y3 – y1) + x3 (y1 – y2)|
= \(\frac{1}{2}\) |1(16 – (- 5) )+ (- 4) (- 5 _ (- 1)) + (- 3) (- 1 – 6)|
= \(\frac{1}{2}\) |11 + 16 + 21|
= \(\frac{1}{2}\) |48| = 24
∴ ∆ ABC వైశాల్యం = 24 చదరపు యూనిట్లు.
ప్రశ్న 19.
బిందువులు A(5, 2), B(4, 7) C(7, – 4)లు శీర్షాలుగా గల త్రిభుజ యొక్క వైశాల్యం కనుగొనండి.
సాధన.
A(1, – 1), B (- 4, 6), C(- 3, – 5) లు శీర్షాలుగా గల త్రిభుజ వైశాల్యం = \(\frac{1}{2}\) |x1 (y2 – y3) + x2 (y3 – y1) + x3 (y1 – y2)|
= \(\frac{1}{2}\) |5(7 – (- 4)) + 4(- 4 – 2) + 7(2 – 7)|
= \(\frac{1}{2}\) |5(11) + 4(- 6) + 7(- 5)|
= \(\frac{1}{2}\)|55 – 24 – 35|
= \(\frac{1}{2}\) |- 4|
= \(\frac{1}{2}\) × 4 = 2
∴ త్రిభుజ వైశాల్యం = 24 చదరపు యూనిట్లు.
![]()
ప్రశ్న 20.
బిందువులు A(- 5, 7), B (- 4, – 5), C(- 1, – 6) మరియు D(4, 5) లు ఒక చతుర్భుజం యొక్క శీర్షాలు అయిన , ABCD చతుర్భుజ. వైశాల్యం కనుగొనండి. (పేజీ నెం. 181)
సాధన.
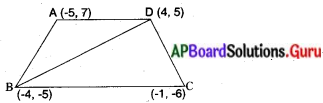
A, B, C, D లు చతుర్భుజం యొక్క శీర్షాలు.
కర్ణము BD, □ABCDA, ∆ABD మరియు ABCD అనే రెండు త్రిభుజాలుగా విభజిస్తుంది.
∆ABD వైశాల్యం = \(\frac{1}{2}\) |- 5 (- 5 – 5) + (- 4) (5 – 7) + 4 (7 – (-5))|
= \(\frac{1}{2}\) |50 + 8 + 48|
= \(\frac{1}{2}\) |106| = 53
చదరపు యూనిట్లు ∆BCD వైశాల్యం = \(\frac{1}{2}\)|- 4(- 6 – 5) + (- 1)(5 + 5) +4(- 5 – (- 6))|
= \(\frac{1}{2}\) |44 – 10 + 4|
= \(\frac{1}{2}\) |38| = 19 చ.యూ.
□ ABCD చతుర్భుజ వైశాల్యం = ∆ABD వైశాల్యం + ∆BCD వైశాల్యం
= 53 + 19 = 72 చదరపు యూనిట్లు
ప్రశ్న 21.
ఒక తలంలో ఉన్న బిందువులు (3, – 2), (- 2, 8) మరియు (0, 4)లు సరేఖీయ బిందువులు అని చూపండి. (పేజీ నెం. 182)
సాధన.
(3, – 2), (- 2, 8) మరియు (0, 4) లతో ఏర్పడే త్రిభుజ వైశాల్యం = \(\frac{1}{2}\) |x1 (y2 – y3) + x2 (y3 – y1) + x3 (y2 – y1)|
= \(\frac{1}{2}\) |3(8 – 4) + (- 2) (4 – (- 2)) + 0 ((- 2) – 8)|
= \(\frac{1}{2}\) |12 – 12| = 0
∴ త్రిభుజ వైశాల్యం సున్నా ‘0’. కావున పై ఇచ్చిన మూడు బిందువులు సరేఖీయ బిందువులు.
![]()
ప్రశ్న 22.
బిందువులు (1, 2), (- 1, b), (- 3, – 4) సరేఖీయాలైతే ‘b’ విలువను కనుగొనండి. (పేజీ నెం. 183)
సాధన.
ఇచ్చిన బిందువులు
A(1, 2), B(- 1, b), C(- 3, – 4) అనుకొనుము.
∆ABC వైశాల్యం = \(\frac{1}{2}\) |x1 (y2 – y3) + x2 (y3 – y1) + x3 (y2 – y1)|
= \(\frac{1}{2}\) |1(b – (- 4)) + (- 1) (- 4 – 2) + (- 3)(2 – b)|
= \(\frac{1}{2}\) |(b + 4) – 1(- 6) – 3(2 – b)|
= \(\frac{1}{2}\) |1(b + 4) + 6 – 6 + 3b|
= \(\frac{1}{2}\) |b + 4 + 6 – 6 + 36|
= \(\frac{1}{2}\) |4b + 4|
= \(\frac{1}{2}\) × 2| 2b + 2 | = |2b + 2| = 0 (∵ ఇచ్చిన బిందువులు సరేఖీయాలు త్రిభుజ వైశాల్యం సున్న)
⇒ 2b + 2 = 0 ⇒ 2b = – 2
∴ b = \(\frac{-2}{2}\) = -1.
ప్రశ్న 23.
12మీ, 9మీ, 15మీ పొడవులు గల భుజాలతో ఏర్పడిన త్రిభుజ వైశాల్యంను “హెరాన్ సూత్రం”ను ఉపయోగించి కనుక్కొందాం. (పేజీ నెం. 183)
సాధన.
A = \(\sqrt{S(S-a)(S-b)(S-c)}\) (∵ S = \(\frac{a+b+c}{2}\))
S = \(\frac{12+9+15}{2}=\frac{36}{2}\) = 18 మీ.
అపుడు
S – a = 18 – 12 = 6 మీ.
S – b = 18 – 9 = 9 మీ.
S – C = 18 – 15 = 3 మీ.
A = \(\sqrt{18(6)(9)(3)}=\sqrt{2916}\) = 54 చదరపు మీటర్లు.
![]()
ప్రశ్న 24.
ఒక రేఖాఖండం యొక్క తొలి, చినరి బిందువుల వరుసగా (2, 3), (4, 5). ఆ రేఖాఖండం యొక్క వాలును కనుగొనండి. (పేజీ నెం. 188)
సాధన.
రేఖాఖండం యొక్క తొలి, చివరి బిందువులు (2, 3), (4, 5) అయిన ఆ రేఖాఖండం వాలు,
m = \(\frac{\mathrm{y}_{2}-\mathrm{y}_{1}}{\mathrm{x}_{2}-\mathrm{x}_{1}}=\frac{5-3}{4-2}=\frac{2}{2}\) = 1
∴ ఇచ్చిన రేఖాఖండం యొక్క వాలు = 1
ప్రశ్న 25.
బిందువులు P(2, 5) మరియు Q(x, 3) ల గుండా పోయే రేఖవాలు 2 అయిన x విలువను కనుగొనుము (పేజీ నెం. 186).
సాధన.
ఇచ్చిన బిందువులు P(2, 5) మరియు Q(x, 3) గుండా పోయే రేఖవాలు 2.
pQ రేఖాఖండం వాలు m = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\) = 2
⇒ \(\frac{3-5}{x-2}\) = 2
⇒ \(\frac{-2}{x-2}\) = – 2
⇒2x – 4 = 2
⇒ x = \(\frac{2}{2}\) = 1
∴ x =1