AP Board 10th Class Maths Solutions Chapter 6 శ్రేఢులు InText Questions

SCERT AP 10th Class Maths Textbook Solutions Chapter 6 శ్రేఢులు InText Questions Textbook Exercise Questions and Answers.

AP State Syllabus 10th Class Maths Solutions 6th Lesson శ్రేఢులు InText Questions

ఇవి చేయండి:

ప్రశ్న 1.
పరిమిత అంకశ్రేణికి 3 ఉదాహరణలు, అనంత అంకశ్రేణికి 3 ఉదాహరణలు ఇమ్ము. (పేజీ నెం. 130)
సాధన.
పరిమిత అంకశ్రేఢులు :
(i) 0, 5, 10, 15, 20, 25
(ii) 50, 47, 44, 41, ………., 11
(iii) 5, 41, 4, 3, ………., \(\frac{1}{2}\)
అనంత అంకశ్రేఢులు :
(i) 0, 5, 10, 15, 20, 25, ………….
(ii) 50, 47, 44, 41, ……………..
ti) 5, 41, 4, 3, ………..

ప్రశ్న2.
ఏదైనా ఒక అంకశ్రేణిని తీసుకొనుము. (పేజీ నెం. 131)
సాధన.
10, 13, 16, 19, 22, ………, 52.

ప్రశ్న 3.
జాబితాలోని ప్రతి పదమునకు ఏదైనా ఒక స్థిర సంఖ్యను కలుపుము. ఫలిత సంఖ్యలను జాబితా రూపంలో రాయుము. (పేజీ నెం. 131)
సాధన.
10 + 2, 13 + 2, 16 + 2, 19 + 2, 22 + 2, …… 52 + 2
జాబితారూపం : 12, 15, 18, 21, 24, ….., 54.

ప్రశ్న 4.
అదే విధంగా అంకశ్రేణిలో ప్రతి పదము నుంచి ఏదైనా ఒక స్థిర సంఖ్యను తీసివేసి ఫలిత సంఖ్యలను జాబితాగా రాయుము. (పేజీ నెం. 131)
సాధన.
10 – 4, 13 – 4, 16 – 4, 19 – 4, 22 – 4, ………., 52 – 4
జాబితారూపం :
6, 9, 12, 15, 18, ……. 48.

ప్రశ్న 5.
అంకశ్రేణిలోని ప్రతి పదమును ఏదైనా ఒక స్థిరసంఖ్యచే గుణించి ఫలిత సంఖ్యలను జాబితాగా రాయుము. మరియు అంకశ్రేణిలోని ప్రతి పదమును ఏదైనా ఒక స్థిరసంఖ్యచే భాగించి ఫలిత సంఖ్యలను జాబితాగా రాయుము. (పేజీ నెం. 131)
సాధన.
a) 10 × 5, 13 × 5, 16 × 5, 19 × 5, 22 × 5, …………, 52 × 5
జాబితారూపం :
50, 65, 80, 95, 110 ……. 260

b) \(\frac{10}{4}\), \(\frac{13}{4}\), \(\frac{16}{4}\), \(\frac{19}{4}\), \(\frac{22}{4}\), ……………… \(\frac{52}{4}\)
జాబితారూపం :
2\(\frac{1}{2}\), 3\(\frac{1}{4}\), 4, 4\(\frac{3}{4}\), 5\(\frac{1}{2}\), ……, 13.

ప్రశ్న 6.
క్రొత్తగా ఏర్పడిన జాబితాలన్నీ అంకశ్రేఢులు అవుతాయేమో పరిశీలించుము. (పేజీ నెం. 132)
సాధన.
క్రొత్తగా ఏర్పడిన జాబితాలు :
12, 15, 18, 21, 24 ………, 54 అంకశ్రేఢి
6, 9, 12, 15, 18 ………., 48 అంకశ్రేఢి
50, 65, 80, 95, 110 ……. 260 అంకశ్రేఢి
2\(\frac{1}{2}\), 3\(\frac{1}{4}\), 4, 4\(\frac{3}{4}\), 5\(\frac{1}{2}\), ……, 13-అంకశ్రేణి
క్రొత్తగా ఏర్పడిన జాబితాలన్నీ అంకశ్రేడులే.

ప్రశ్న 7.
చివరగా నీ అభిప్రాయం ఏమిటి ? (పేజీ నెం. 132)
సాధన.
ఒక అంకశ్రేణిలోని ప్రతి పదానికి ఒక స్థిర సంఖ్యను కలిపినా, తీసివేసినా, గుణించినా, భాగించినా వచ్చే సంఖ్యలు కూడా అంకశ్రేణిలో ఉంటాయి. (భాగహారంలో స్థిర సంఖ్యగా సున్నాను తీసుకోకూడదు.)

ప్రయత్నించండి:

ప్రశ్న 1.
(i) క్రింది వానిలో ఏవి అంకశ్రేఢులు ? ఎందుకు ? (పేజీ నెం. 128)
(a) 2, 3, 5, 7, 8, 10, 15, ……
సాధన.
అంకశ్రేణి కాదు. ఎందుకనగా మొదటి పదం 2కు 1 కలిపితే 2వ పదం 3 వస్తుంది. కాని రెండవ పదంకు 2 కలిపితే 3వ పదం 5 వస్తుంది. ఇక్కడ రెండు సందర్భాలలోను కలుపుతున్న స్థిరసంఖ్య సమానంగా లేదు.

(b) 2, 5, 7, 10, 12, 15, ………….
సాధన.
అంకశ్రేణి కాదు. ఎందుకనగా
మొదటి పదం 2కు 3 కలపడం వలన 2వ పదం 5, అలాగే 2వ పదానికి 2 కలపడం వలన 3వ పదం 7 వస్తున్నది. కాని 3వ పదం 7కు 3 కలపడం వలన 4వ పదం 10 వస్తుంది. అన్ని సందర్భాలలోను
కలుపుతున్న స్థిరసంఖ్య సమానంగా లేదు.

(c) – 1, – 3, – 5, – 1, …………..
సాధన.
అంకశ్రేణి. ఎందుకనగా ..
మొదటి పదం – 1కు – 2 కలిపిన 2వ పదం -3, – 2వ పదం – 3కు – 2 కలిపిన 3వ పదం – 5, 3వ పదం .- 5కి – 2 కలిపిన 4వ పదం – 7 వస్తుంది. అన్ని సందర్భాలలోను ఒకే స్థిరసంఖ్య – 2 ను
కలుపుతున్నాము.

(ii) ఏవైనా మూడు అంకశ్రేఢులను రాయుము. (పేజీ నెం. 128)
సాధన.
(i) 1, 4, 7, 10, 13, 16, ………….
(ii) 4, 1, -2, -5, -8, ………….
(iii) 5, 15, 25, 35, 45, …………

ఆలోచించి, చర్చించి, రాయండి:

(a) ఒక పాఠశాలలో ప్రార్థనా సమయంలో వరుసగా నిలబడిన విద్యార్థుల ఎత్తులు (సెం.మీ.లలో) 147, 148, 149, ……. 157. (పేజీ నెం. 129)
(b) ఒక పట్టణములో జనవరి మాసంలో ఒక వారంలో నమోదైన కనిష్ట ఉష్ణోగ్రతల ఆరోహణ క్రమము – 3.1, – 3.0, – 2.9, – 2.8, – 2.7, – 2.6, – 2.5
(c) ₹ 1000 ల అప్పు 5% సొమ్మును ప్రతీ నెల చెల్లిస్తున్న, ప్రతి నెల చివర ఇంకనూ చెల్లించవలసిన సొమ్ము ₹ 950, ₹ 900, ₹ 850, ₹ 800, …, ₹ 50.
(d) ఒక పాఠశాలలో 1 నుంచి 12వ తరగతి వరకూ ప్రతి తరగతిలో అత్యధిక మార్కులు సాధించిన వారికి ఇచ్చే బహుమతుల విలువ వరుసగా ₹ 200, ₹ 250, ₹ 300, ₹ 350, ……₹ 750
(e) 10 నెలలలో ప్రతి నెలలో ₹ 50 లు చొప్పున పొదుపు చేసిన ప్రతినెల చివరలో ఉండే మొత్తం సొమ్ము వరుసగా ₹ 50, ₹ 100, ₹ 150, ₹ 200, ₹ 250, ₹ 300,
₹ 350, ₹ 400, ₹ 450, ₹ 500.

ప్రశ్న 1.
పైన పేర్కొనబడిన ప్రతి జాబితా ఏవిధంగా అంకశ్రేణి అవుతుందో ఆలోచించుము. మీ మిత్రునితో చర్చించుము.(పేజీ నెం. 129)
సాధన.
(a) 147 , 148, 149, …….., 157
సామాన్యభేదం
d = 148 – 147 = 149 – 148 = …… = 1
జాబితాలోని ప్రతిపదం దాని ముందున్న పదానికి 1 కలపడం వలన వస్తుంది. కావున అంకశ్రేఢి అవుతుంది.

(b) – 3.1, – 3.0, – 2.9, – 2.8, – 2.7, – 2.6, – 2.5
సామాన్య భేదం d = – 3.0 – (-3.1)
= – 2.9 – (- 3.0) = …….. = 0.1
సామాన్యభేదం (d) అన్ని సందర్భాలలోను సమానం. కావున అంకశ్రేణి అవుతుంది.

(c) 950, 900, 850, 800, ……, 50
సామాన్యభేదం d = 900 – 950
= 850 – 900 = ….. = – 50
సామాన్య భేదం (d) అన్ని సందర్భాలలోను సమానం. కావున అంకశ్రేణి అవుతుంది.

(d) 200, 250, 300, 350, . . . . ., 750
సామాన్యభేదం d = 250 – 200
= 300 – 250 = …. = 50
సామాన్యభేదం (d) అన్ని సందర్భాలలోను సమానం. కావున అంకశ్రేణి అవుతుంది.

(e) 50, 100, 150, 200, 250, 300, 350, 400, 450, 500
సామాన్యభేదం d = 100 – 50
= 150 – 100 = …… = 50,
సామాన్యభేదం (d) అన్ని సందర్భాలలోను సమానం. కావున అంకశ్రేణి అవుతుంది.

ప్రశ్న 2.
పైన ఇవ్వబడిన ప్రతి జాబితాకు సామాన్యభేదంను కనుగొనుము. సామాన్యభేదం ఎప్పుడు ధనాత్మకమో ఆలోచించుము. (పేజీ నెం. 129)
సాధన.
(a) సామాన్యభేదం d = 148 – 147 = 1
(b) సామాన్యభేదం d = – 3.0 – (- 3.1) = – 3.0 + 3.1= 0.1
(c) సామాన్యభేదం d = 900 – 950 = – 50
(d) సామాన్యభేదం d = 250 – 200 = 50
(e) సామాన్యభేదం d = 100 – 50 = 50
అంకశ్రేణిలోని పదాలు ఆరోహణక్రమంలో ఉంటే సామాన్యభేధం ధనాత్మకము.

ప్రశ్న 3.
సామాన్యభేదం ఒక చిన్న ధనాత్మక విలువ వుండేటట్లు ఒక అంకశ్రేణిని తయారుచేయుము. (పేజీ నెం. 129)
సాదన.
2, 2.1, 2.2, 2.3, 2.4, ………, 3.

ప్రశ్న 4.
సామాన్యభేదం ఒక పెద్ద ధనాత్మక విలువగా వుండేటట్లు ఒక
అంకశ్రేణిని తయారుచేయుము. (పేజీ నెం. 129)
సాధన.
2, 1002, 2002, 3002, 4002, ……..

ప్రశ్న 5.
సామాన్య భేదం ఋణాత్మకంగా వుండేటట్లు ఒక అంకశ్రేణిని రాయుము. (పేజీ నెం. 129)
సాధన. 20, 16, 12, 8, 4, 0, ……….

కృత్యము:

(i) అగ్గిపుల్లల సహాయంతో క్రింది ఆకారాలను ఏర్పరచుము. :(పేజీ నెం. 129)

సాధన.

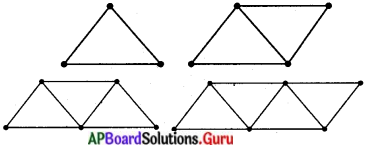
(ii) ప్రతి ఆకారానికి కావలసిన అగ్గిపుల్లల సంఖ్యను వరుసగా రాయుము. (పేజీ నెం. 129)
సాధన.
అగ్గిపుల్లల సంఖ్య 3, 5, 7, 9.

(iii) జాబితాలో రెండు వరుస సంఖ్యల మధ్య గల భేదం ఒకే విధంగా (స్థిరంగా) ఉందా ? (పేజీ నెం. 130)
సాధన.
రెండు వరుస సంఖ్యల మధ్యగల భేదం ఒకే విధంగా 2కు సమానంగా ఉంది.

(iv) ఈ సంఖ్యల జాబితా ఒక అంకశ్రేణి అవుతుందా ?
సాధన.
అవును, అంకశ్రేణి అవుతుంది. . (పేజీ నెం. 130)

ఇవి చేయండి:

ప్రశ్న 1.
క్రింద ఇవ్వబడిన ప్రతి అంకశ్రేణిలో పేర్కొన్న పదాల మొత్తమును కనుగొనుము. (పేజీ నెం. 143)

(i) 16, 11, 6, ………., 23 పదాలు.
సాధన.
a = 16, d = a₂ – a₁ = 11 – 16 = – 5, n = 23
S_n = \(\frac{n}{2}\) [2a + (n – 1) d]
23 పదాల మొత్తం S₂₃ = \(\frac{23}{2}\) [2(16) + (23 – 1)(- 5)]
= \(\frac{23}{2}\) [32 – 110]
= \(\frac{23 \times(-78)}{2}\) = – 23 × 39 = – 897

(ii) – 0.5, – 1.0, – 1.5, ………….., 10 పదాలు.
సాధన.
a = – 0.5, d = a₂ – a₁ = (- 1.0) – (- 0.5) = – 0.5, n = 10
∴ S_n = \(\frac{n}{2}\) [2a + (n – 1) d]
S₁₀ = \(\frac{10}{2}\) [2(- 0.5) + (10 – 1)(- 0.5)]
= \(\frac{10}{2}\) [- 1.0 + 9(- 0.5)]
= 5[- 1.0 – 4.5]
= 5[- 5.5] = – 27.5
S₁₀ = – 27.5

(iii) -1, \(\frac{1}{4}\), \(\frac{3}{2}\), ……. 10 పదాలు.
సాధన.
a = – 1, d = a₂ – a₁
= \(\frac{1}{4}\) – (- 1) = 1 + \(\frac{1}{4}\) = \(\frac{5}{4}\)
n = 10
∴ S_n = \(\frac{n}{2}\) [2a + (n – 1) d]
S₁₀ = \(\frac{10}{2}\) [2(- 1) + (10 – 1)(\(\frac{5}{4}\))]
= 5[- 2 + 9 × \(\frac{5}{4}\)]
= 5[- 2 + \(\frac{45}{4}\)]
= 5 \(\left[\frac{-8+45}{4}\right]\)
S₁₀ = \(\frac{5 \times 37}{4}=\frac{185}{4}\) = 46.25.

ఇవి చేయండి:
క్రింది వానిలో గుణశ్రేడులు కానివేవో కొనుగొనుము.

ప్రశ్న 1.
6, 12, 24, 48, …………
సాధన.
\(\frac{a_{2}}{a_{1}}=\frac{12}{6}\) = 2;

\(\frac{a_{3}}{a_{2}}=\frac{24}{12}\) = 2;

\(\frac{a_{4}}{a_{3}}=\frac{48}{24}\) = 2
ప్రతి సందర్భంలోను \(\frac{a_{n}}{a_{n-1}}\) = 2
కావున గుణ శ్రేఢి అవుతుంది.

ప్రశ్న 2.
1, 4, 9, 16, …………….
సాధన.
\(\frac{a_{2}}{a_{1}}=\frac{4}{1}\) = 2;
\(\frac{a_{3}}{a_{2}}=\frac{9}{4}\) = 2;
\(\frac{a_{4}}{a_{3}}=\frac{16}{9}\) = 2 ………….
అన్ని సందర్భాలలో \(\frac{a_{n}}{a_{n-1}}\) సమానంకాదు. కావున గుణశ్రేణి కాదు.

ప్రశ్న 3.
1, – 1, 1, – 1, ………………….
సాధన.
అన్ని పదాలు ‘శూన్యేతరాలు.
\(\frac{a_{2}}{a_{1}}=\frac{-1}{1}\) = – 1;

\(\frac{a_{3}}{a_{2}}=\frac{1}{-1}\) = – 1,

\(\frac{a_{4}}{a_{3}}=\frac{-1}{1}\) = – 1
అన్ని సందర్భాలు \(\frac{a_{n}}{a_{n-1}}\) = 1
కావున ఇది గుణశ్రేణి అవుతుంది.

ప్రశ్న 4.
– 4, – 20, – 100, – 500, ………..
సాధన.
అన్ని పదాలు శూన్యేతరాలు.
\(\frac{a_{2}}{a_{1}}=\frac{-20}{-4}\) = 5;

\(\frac{a_{3}}{a_{2}}=\frac{-100}{-20}\) = 5;

\(\frac{a_{4}}{a_{3}}=\frac{-500}{-100}\) = 5
అన్ని సందర్భా లలో \(\frac{a_{n}}{a_{n-1}}\) = 5.
కావున ఇది గుణ శ్రేణి అవుతుంది.

ఆలోచించి, చర్చించి, రాయండి:

ప్రశ్న 1.
క్రింద ఇచ్చిన ప్రతి జాబితా ఎందుకు గుణశ్రేఢి అవుతుందో వివరించుము. (పేజీ నెం. 149)
1వ జాబితా : 1, 4, 16, 64, 256, ……….
సాధన.
1, 4, 16, 64, 256, …………….
ఇప్పుడు \(\frac{a_{2}}{a_{1}}=\frac{a_{3}}{a_{2}}=\frac{a_{4}}{a_{3}}=\frac{a_{5}}{a_{4}}\) = 4
కావున ఇది గుణశ్రేణి.

2వ జాబితా : 550, 605, 665.5, …………….
అన్ని పదాలు శూన్యేతరాలు మరియు
\(\frac{\mathrm{a}_{2}}{\mathrm{a}_{1}}=\frac{605}{550}=\frac{11}{10}\)
\(\frac{a_{3}}{a_{2}}=\frac{665.5}{60.5}=\frac{6655}{6050}=\frac{11}{10}\)
ప్రతి సందర్భం లోను \(\frac{a_{n}}{a_{n-1}}\) = \(\frac{11}{10}\)
కావున ఇది గుణశ్రేణి.

3వ జాబితా : 256, 128, 64, 32, …………
అన్ని పదాలు శూన్యేతరాలు మరియు
\(\frac{a_{2}}{a_{1}}=\frac{128}{256}=\frac{1}{2}\);
\(\frac{a_{3}}{a_{2}}=\frac{64}{128}=\frac{1}{2}\);
\(\frac{a_{4}}{a_{3}}=\frac{32}{64}=\frac{1}{2}\)
ప్రతి సందర్భం లోను \(\frac{a_{n}}{a_{n-1}}\) = \(\frac{1}{2}\)
కావున ఇది గుణశ్రేణి.

4వ జాబితా : 18, 16.2, 14.58, 13.122, ……..
సాధన.
18, 16.2, 14.58, 13.122, ………..
అన్ని పదాలు శూన్యేతరాలు మరియు
\(\frac{a_{2}}{a_{1}}=\frac{16.2}{18}=\frac{162}{180}=\frac{9}{10}\) = 0.9
\(\frac{a_{3}}{a_{2}}=\frac{14.58}{16.2}=\frac{1458}{1620}\) = 0.9
\(\frac{a_{4}}{a_{3}}=\frac{13.122}{14.58}=\frac{13122}{14580}\) = 0.9
అన్ని సందర్భాలలో \(\frac{a_{n}}{a_{n-1}}\) = 0.9 (సమానము).
కావున ఇది గుణ శ్రేఢి అవుతుంది.

ప్రశ్న 2.
ఒక గుణశ్రేణిని నిర్ణయించుటకు కావలసిన అంశాలేమిటి ? (పేజీ నెం. 149)
సాధన.
ఒక గుణ శ్రేణిని నిర్ణయించుటకు కావలసిన అంశాలు: అన్ని పదాలు శూన్యేతరాలు మరియు
1) మొదటి పదము
2) సామాన్య నిష్పత్తి
3) శ్రేణిలోని పదాల సంఖ్య.

ఉదాహరణలు:

ప్రశ్న 1.
అంకశ్రేణి \(\frac{1}{4}\), \(\frac{-1}{4}\), \(\frac{-3}{4}\), \(\frac{-5}{4}\), ……, లో మొదటి పదం a ను, సామాన్య భేదం d లను కనుగొనుము. (పేజీ నెం. 132)
సాధన.
మొదటి పదం a = \(\frac{1}{4}\)
సామాన్య భేదం d = \(\frac{-1}{4}\) – \(\frac{4}{4}\)
= \(\frac{-1-1}{4}\)
= \(\frac{-2}{4}\) = \(\frac{-1}{2}\).

ప్రశ్న 2.
క్రింది వానిలో ఏవి అంకశ్రేఢులు? ఒకవేళ అంకశ్రేణి అయితే తరువాత వచ్చే రెండు పదాలను కనుగొనుము. (పేజీ నెం. 132)
(i) 4, 10, 16, 22, . . .
సాధన.
d = a₂ – a₁ = 10 – 4 = 6
d = a₃ – a₂ = 16 – 10 = 6
d = a₄ – a₃ = 22 – 16 = 6
ప్రతిసారి సామాన్యభేదం (d) సమానము.
కావున ఇచ్చిన జాబితా ఒక అంకశ్రేణి. జాబితాలో తరువాత రెండు పదాలు : 22 + 6 = 28 మరియు 28 + 6 = 34.

(ii) 1, – 1, – 3, – 5, . . . . .
సాధన.
d = a₂ – a₁ = – 1 – 1 = – 2
d = a₃ – a₂ = – 3 – (- 1)
= – 3 + 1 = – 2
d = a₄ – a₃ = – 5 – (- 3)
= – 5 + 3 = – 2
ప్రతిసారి సామాన్యభేదం (d) సమానము.
కావున ఇచ్చిన జాబితా ఒక అంకశ్రేణి.
జాబితాలో తరువాత రెండు పదాలు : – 5 + (- 2) = – 7 మరియు – 7 + (- 2) = – 9.

(iii) – 2, 2, – 2, 2, – 2, …….
సాధన.
d = a₂ – a₁ = 2 – (- 2) = 2 + 2 = 4
d = a₃ – a₂ = – 2 – 2 = – 4
ఇక్కడ a₂ – a₁ ≠ a₃ – a₂ కావున అంకశ్రేణి కాదు.

(iv) 1, 1, 1, 2, 2, 2, 3, 3, 3, …………..
సాధన.
d = a₂ – a₁ = 1 – 1 = 0
d = a₃ – a₂ = 1 – 1 = 0
d = a₄ – a₃ = 2 – 1 = 1
ఇచ్చట, a₂ – a₁ = a₃ – a₂ ≠ a₄ – a₂
అనగా ఇచ్చిన సంఖ్యల జాబితా అంకశ్రేణి కాదు.

(v) x, 2x, 3x, 4x ………..
సాధన.
d = a₂ – a₁ = 2x – x = x
d = a₃ – a₂ = 3x – 2x = x
d = a₄ – a₃ = 4x – 3x = x
ప్రతిసారి సామాన్యభేదం (d) సమానం.
కావున ఇచ్చిన జాబితా ఒక అంకశ్రేణి.
జాబితాలో తరువాత 2 పదాలు : 4x + x = 5x మరియు 5x + x = 6x.

ప్రశ్న 3.
5, 1, – 3, – 7 . . . అంకశ్రేణిలో. 10వ పదమును కనుగొనుము. (పేజీ నెం. 136)
సాధన.
5, 1, -3, -7. . . .
a = 5, d = a₂ – a₁ = 1 – 5 = – 4 మరియు n = 10.
n వ పదం a_n = a + (n – 1) d
a₁₀ = 5 + (10 – 1) (- 4)
= 5 – 36 = – 31
∴ అంకశ్రేణిలో 10వ పదము = -31.

ప్రశ్న 6.
21, 18, 15, ……. అంకశ్రేణిలో ఎన్నవ పదము ‘- 81’ అవుతుంది ? ఏదైనా ఒక పదము ‘0’ అవుతుందా ? నీ సమాధానమునకు కారణాలిమ్ము. (పేజీ నెం. 136)
సాధన.
ఇచ్చిన అంకశ్రేణి 21, 18, 15, ……
a = 21, d = a₂ – a₁ = 18 – 21 = – 3 మరియు a_n = – 81.
n వ పదం a_n = a + ( n – 1) d
– 81 = 21 + (n – 1) (- 3)
– 81 = 21 – 3n + 3
– 81 = 24 – 31
– 81-24 = – 3n
– 105 = – 3n
\(\frac{105}{3}\) = 35
∴. n = 35.
అనగా పై అంకశ్రేణిలో 35వ పదము – 81 అవుతుంది.
తరువాత ఒక పదం 0 అవుతుందా అనగా a_n = 0.
అయ్యే విధంగా n ∈ N అయ్యేటట్లు nను కనుగొనాలి.
a_n = a + (n – 1) 4 = 0
21 + (n – 1) (- 3) = 0
21 – 3n + 3 = 0
24 = 3n
n = \(\frac{24}{3}\) = 8
n = 8 మరియు 8 ∈ N అనగా అంకశ్రేణిలో 8వ పదము సున్నా అవుతుంది.

ప్రశ్న 7.
3వ పదము 5; 7వ పదము 9గా వుండునట్లు ఒక అంకశ్రేణిని కనుగొనుము. (పేజీ నెం. 137)
సాధన.
లెక్క ప్రకారం,
a₃ = a + 2d = 5 ……. (1)
a₇ = a + 6d = 9……… (2)
సమీకరణాలు (1) మరియు (2) ల నుంచి,
(2) – (1)

d = 1 ను (1) లో ప్రతిక్షేపించగా,
a + 2(1) = 5
⇒ a = 5 – 2 = 3
∴ a = 3, 4 = 1.
∴ కావలసిన అంకశ్రేణి : 3, 4, 5, 6, 7, 8, 9 ………..

ప్రశ్న 8.
5, 11, 17, 23, . . . జాబితాలో 301 ఉంటుందో లేదో కనుగొనుము. (పేజీ నెం. 137)
సాధన.
ఇచ్చిన జాబితా
5, 11, 17, 23, . . . .
a₂ – a₁= 11 – 5 = 6,
a₃ – a₂ = 17 – 11 = 6,
a₄ – a₃ = 23 – 17 = 6
……………………….
అన్ని సందర్భాలలో a_{k + 1} – a_k సమానము.
∴ ఇచ్చిన జాబితా ఒక అంకశ్రేఢి అవుతుంది.
ఈ అంకశ్రేణిలో a = 5, d = 6 మరియు ఈ జాబితాలో nవ పదం a_n = 301 అనుకొందాం.
అప్పుడు, a_n = a + (n – 1) d = 301
= 5 + (n – 1) 6 = 301
= 5 + 6n – 6 = 301
6n – 1 = 301
6n = 301 + 1 = 302
n = \(\frac{302}{6}=\frac{151}{3}\)
పదాల సంఖ్య ఎల్లప్పుడు ఒక సహజ సంఖ్య అవుతుంది.
కాని \(\frac{151}{3}\) సహజసంఖ్య కాదు. కావున 301 ఇచ్చిన జాబితాలో ఉండదు.

ప్రశ్న 9.
3 చే భాగించబడే రెండంకెల సంఖ్యలు ఎన్ని ? (పేజీ నెం. 137)
సాధన.
3చే భాగించబడే రెండంకెల సంఖ్యల జాబితా : 12, 15, 18, 21, …………., 99
ఇది ఒక అంకశ్రేణి, ఇక్కడ a = 12, d = 3 మరియు a_n = 99.
a_n = a + (n – 1) d = 99
= 12 + (n – 1) 3 = 99
= 12 + 3n – 3 = 99
3n + 9 = 99
3n = 99 – 9 = 90
n = \(\frac{90}{3}\) = 30
∴ 3చే భాగించబడే రెండంకెల సంఖ్యలు 30 కలవు.

ప్రశ్న 10.
10, 7, 4, . . ., – 62 అంకశ్రేణిలో చివరి నుంచి 11వ పదమును కనుగొనుము. (పేజీ నెం. 138)
సాధన.
ఇచ్చిన అంకశ్రేఢి 10, 7, 4, …….., – 62 లో చివరి
నుంచి 11వ పదమును కనుగొనవలెనన్న ముందుగా ఈ శ్రేణిలో ఎన్ని పదాలున్నాయో కనుగొనవలెను.
∴ a = 10, d = a₂ – a₁ = 7 – 10 = – 3,
a_n = – 62
a_n = a + (n – 1) d = – 62.
= 10 + (n – 1) (- 3) = – 62
10 – 3n + 3 = – 62
– 3n = – 62 – 13 = – 75
3n = 75
⇒ n = \(\frac{175}{3}\) = 25
∴ n = 25.
అనగా ఇవ్వబడిన శ్రేణిలో 25 పదాలుంటాయి. (25 – 11) + 1 = 14 + 1 = 15
కావున చివరి నుండి 11వ పదం మొదటి నుండి 15వ పదం అవుతుంది.
∴ a₁₅ = 10 + (15 – 1) (- 3)
= 10 + (14) (-3)
= 10 – 42 = – 32
∴ చివరి నుండి 11వ పదం = – 32.

ప్రశ్న 11.
₹ 1000 లకు సంవత్సరానికి 8% బారు వడ్డీ ప్రకారము ప్రతి సంవత్సరానికి అయ్యే వడ్డీని కనుగొనుము. ఈ వడ్డీల జాబితా ఒక అంకశ్రేణి అవుతుందా ? ఒకవేళ అంకశ్రేణి అయితే 30వ సం||ము చివర అయ్యే వడ్డీని కనుగొనుము. (పేజీ నెం. 138)
(లేదా)
రూ. 1,000 లను 8% బారువడ్డీ చొప్పున ప్రతి సంవత్స రానికి అయ్యే వడ్డీని లెక్కగట్టుము. 1వ, 2వ మరియు 3వ సంవత్సరాలకు అయిన వడ్డీలు అంకశ్రేణిని సూచిస్తాయా? అయితే 30 సంవత్సరాలకు చెల్లించవలసిన మొత్తం వడ్డీ ఎంత ?
సాధన.
అసలు = ₹ 1000, R = 8%
బారువడ్డీ I = \(\frac{\mathrm{PTR}}{100}\)
∴ 1వ సం||ము చివర అయ్యే వడ్డీ = \(\frac{1000 \times 8 \times 1}{100}\) = ₹ 80

2వ సం||ము చివర అయ్యే వడ్డీ = \(\frac{1000 \times 8 \times 2}{100}\)= ₹ 160

3వ సం||ము చివర అయ్యే వడ్డీ = \(\frac{1000 \times 8 \times 3}{100}\) = ₹ 240

4వ సం||ము చివర అయ్యే వడ్డీ = \(\frac{1000 \times 8 \times 4}{100}\) = ₹ 320
………………………………………………..
………………………………………………..

∴ 1వ, 2వ, 3వ, 4వ సం||ల చివర అయ్యే వడ్డీల విలువలు వరుసగా 80, 160, 240, 320, ………….
పై జాబితాలో ఏ రెండు వరుస పదాల భేదము (80) స్థిరము.
కావున ఇది ఒక అంకశ్రేణి అవుతుంది. 30 సం||ల చివర అయ్యే వడ్డీని 230 అవుతుంది.
∴ a₃₀ = a + (30 – 1) d
= 80 + 29 × 80
= 80 + 2320
a₃₀ = 2400
30 సం||ముల చివర అయ్యే వడ్డీ = ₹ 2400.
(లేదా)
∴ 30 సంవత్సరాలలో చెల్లించు మొత్తం వడ్డీ = S₃₀ = \(\frac{n}{2}\) (a + 1)
= \(\frac{30}{2}\) (80 + 2400)
= 15 × 2840 = రూ. 37200.

ప్రశ్న 12.
ఒక పూలపాదులో మొదటి వరుసలో 23 గులాబీ చెట్లు, రెండవ వరుసలో 21, మూడవ వరుసలో 19 ….. ఉన్నాయి. చివరి వరుసలో 5 చెట్లు ఉన్న ఎన్ని వరుసలలో గులాబీ చెట్లు కలవు ? (పేజీ నెం. 139)
సాధన.
1వ, 2వ, 3వ, ……. వరుసలలో గల గులాబీ చెట్లు 23, 21, 19, ………, 5
ఏ రెండు వరుస పదాల భేదమైనా 2. కావున అంకశ్రేణి.
∴ పూలపాదులలోని వరుసల సంఖ్య n అయిన a = 23, d = 21 – 23 = – 2 మరియు a_n = 5
a_n = a + (n – 1) d = 5
= 23 + (n – 1) (- 2) = 5
= 23 – 2n + 2 = 5
= 25 – 2n = 5
= – 2n = 5 – 25 = – 20
∴ 2n = 20
n = \(\frac{20}{2}\) = 10
∴ n = 10
∴ పూలపాదులోని వరుసల సంఖ్య = 10.

ప్రశ్న 13.
ఒక అంకశ్రేణిలో మొదటి పదం 10 మరియు మొదటి 14 పదాల మొత్తము 1050 అయిన 20వ పదమును కనుగొనుము. (పేజీ నెం. 143)
సాధన.
ఇక్కడ a = 10, S₁₄ = 1050, n = 14
S_n = \(\frac{n}{2}\) [2a + (n – 1) d]
S₁₄ = \(\frac{10}{2}\) [2(10) + (14 – 1) d] = 1050
7 [20 + 13d] = 1050
140 + 91d = 1050
91d = 1050 – 140 = 910
d = \(\frac{910}{91}\) = 10
∴ 20 వ పదం a₂₀ = 10 + (20 – 1) 10
[a_n = a + (n – 1) d].
= 10 + 190
a₂₀ = 200.

ప్రశ్న 14.
24, 21, 18, . .. అంకశ్రేణిలో ఎన్ని పదాల మొత్తం 78 అవుతుంది ? (పేజీ నెం. 143)
సాధన.
ఇచ్చట a = 24, d = a₂ – a₁
= 21 – 24 = – 3,
S_n = 78, n = ?
S_n = \(\frac{n}{2}\) [2a + (n – 1) d] = 78
= \(\frac{n}{2}\) [48 + (n – 1) ( – 3)] = 78
= \(\frac{n}{2}\) [ 48 – 3n + 3] = 78
= \(\frac{n}{2}\) [51 – 3n] = 78
51n – 3n² = 78 X 2 = 156
– 3n² + 51n – 156 = 0
– 3 [n² – 17n + 52] = 0
n² – 17n + 52 = 0
n² – 4n – 13n + 52 = 0
n (n – 4) – 13 (n – 4) = 0
(n – 4) (n – 13) = 0
∴ n – 4 = 0 లేదా n – 13 = 0
⇒ n = 4 లేదా 13 n యొక్క రెండు విలువలు సహజసంఖ్యలే కావున రెండు విలువలు తీసుకొనవచ్చును. అనగా పదాల సంఖ్య 4 లేదా 13.

ప్రశ్న 15.
క్రింది వాని మొత్తాలను కనుగొనుము.
(i) మొదటి 1000 ధనపూర్ణ సంఖ్యలు
(ii) మొదటి nధనపూర్ణ సంఖ్యలు (పేజీ నెం. 144)
సాధన.
(i) మొదటి 1000 ధనపూర్ణ సంఖ్యల జాబితా 1, 2, 3, 4, 5, 6, 7, …….. 1000 , ఇవి A.P లో కలవు.
a = 1, d = 2 – 1 = 1; n = 1000 మరియు l = 1000 (∵ l చివరి పదము)
S_n = \(\frac{n}{2}\) (a + l)
S₁₀₀₀ = \(\frac{1000}{2}\) (1 + 1000)
= 500 × 1001
S₁₀₀₀ = 500500
మొదటి 1000 ధనపూర్ణ సంఖ్యల మొత్తం = 500500.

(ii) మొదటి n ధనపూర్ణ సంఖ్యల జాబితా – 1, 2, 3, 4, 5, …….., n . ఇవి A.P. లో కలవు.
a = 1, d = 2 – 1 = 1, n = n, 1 = n
S_n = 2 [a + l]
∴ S_n = 2 [1 + n]
S_n = \(\frac{n(n+1)}{2}\)
∴ మొదటి n ధనపూర్ణ సంఖ్యల మొత్తం S_n = \(\frac{n(n+1)}{2}\)

ప్రశ్న 16.
a_n = 3+ 2n ను 1వ పదంగా కలిగిన శ్రేణి యొక్క మొదటి 24 పదాల మొత్తాన్ని కనుగొనుము. (పేజీ నెం. 144)
సాధన.
a_n = 3 + 2n,
a₁ = 3 + 2 × 1 = 5
a₂ = 3 + 2 × 2 = 7
a₃, = 3 + 2 × 3 = 9
…………………………..
……………………………
……………………………
సంఖ్యల జాబితా = 5, 7, 9, 11, ………….. ఈ జాబితా A.P. లో కలదు.
ఇచ్చట a = 5, d = a₂ – a₁ = 7 – 5 = 2, n = 24
S_n = \(\frac{n}{2}\) [2a + (n – 1)d]
S₂₄ = \(\frac{24}{2}\) [2(5) + (24 – 1) (2) |
= 12 [10 + 46]
S₂₄ = 12 × 56 = 672
ఇచ్చిన శ్రేణిలో 24 పదాల మొత్తం S₂₄4 = 672.

ప్రశ్న 17.
ఒక టెలివిజన్ తయారీ కంపెనీ 3వ సం||ములో 600 టెలివిజన్లను, 7వ సం||ము 700 టెలివిజన్ సెట్లను తయారు చేసింది. ఇది తయారీ చేసే టెలివిజన్ల సంఖ్య ప్రతీ సం||ము స్థిరంగా పెరుగుతూ ఉంటే
(i) 1వ సం||ములో అది తయారు చేసిన టెలివిజన్ల సంఖ్య
(ii) 10వ సం||ములో అది తయారు చేసిన టెలివిజన్ల సంఖ్య
(iii) మొదటి 7 సంవత్సరాలలో అది తయారు చేసిన మొత్తం సెట్ల సంఖ్యను కనుగొనుము. (పేజీ నెం. 145)
సాధన.
(i) ప్రతి సంవత్సరము తయారుచేసే టెలివిజన్ సెట్ల సంఖ్య ఒక స్థిర విలువతో పెరుగుతూ వుంటే 1వ, 2వ, 3వ, …., సం||లలో తయారయ్యే టెలివిజన్ సెట్ల సంఖ్యల జాబితా ఒక అంకశ్రేఢిని ఏర్పరుస్తుంది.
n వ సం||లో తయారుచేసే టెలివిజన్ సెట్ల సంఖ్యను a_n అనుకొనుము.
లెక్క ప్రకారం,a₃ = 600 మరియు a₇ = 700
⇒ a + 2d = 600 ………. (1)
a + 6d = 700 ……… (2)

d = 25 ను (1) లో రాయగా
a + 2(25) = 600
a + 50 = 600
a = 600 – 50 = 550
∴ మొదటి సంవత్సరంలో తయారైన టెలివిజన్ సెట్ల సంఖ్య = 550.

(ii) a₁₀ = a + 9d
= 550 + 9 × 25
= 550 + 225 = 775
∴ 10వ సం||లో తయారుచేసిన టెలివిజన్ సెట్ల సంఖ్య = 775.

(iii) S₇ = \(\frac{7}{2}\) [12 × 550 + (7 – 1) × 25]
= \(\frac{7}{2}\) [1100 + 150]
= \(\frac{7}{2}\) [1250] = 4375
అనగా మొదటి 7 సం||లలో తయారైన మొత్తం టెలివిజన్ సెట్ల సంఖ్య = 4375.

ప్రశ్న 18.
మొదటి పదము a = 3, సామాన్య నిష్పత్తి r = 2 అయిన గుణశ్రేణిని రాయుము. పేజీ నెం. 150)
సాధన.
మొదటి పదం a = 3
సామాన్యనిష్పత్తి r = 2
∴ రెండవ పదము = ar = 3 × 2 = 6
మూడవ పదము = 6 × 2 = 12
………………………………..
………………………………..
………………………………..
గుణశ్రేఢి: 3, 6, 12, 24, ………….

ప్రశ్న 19.
a = 256, r = \(\frac{-1}{2}\) అయిన గుణశ్రేణిని రాయుము. (పేజీ నెం. 150)
సాధన.
గుణశ్రేఢి సాధారణ రూపము = a, ar, ar², ar³, …………..
= 256, 256(\(\frac{-1}{2}\)), 257(\(\frac{-1}{2}\))², 256(\(\frac{-1}{2}\))³
= 256, – 128, 64, – 32, …….

ప్రశ్న 20.
గుణశ్రేణి 25, – 5, 1, 3 యొక్క సామాన్య నిష్పత్తిని కనుగొనుము. (పేజీ నెం. 150)
సాధన.
సామాన్య నిష్పత్తి r = \(\frac{a_{2}}{a_{1}}=\frac{-5}{25}=\frac{-1}{5}\)
గుణశ్రేఢి : 3, 6, 12, 24, ………

ప్రశ్న 21.
క్రింది జాబితాలో ఏవి గుణశ్రేణిలు అవుతాయి.
(i) 3, 6, 12, ……….
(ii) 64, – 32, 16, …………..
(iii) \(\frac{1}{64}\), \(\frac{1}{32}\), \(\frac{1}{8}\), ………
సాధన.
(i) 3, 6, 12, ……….
అన్ని పదాలు శూన్యేతరాలు మరియు
\(\frac{a_{2}}{a_{1}}=\frac{6}{3}\) = 2;
\(\frac{a_{3}}{a_{2}}=\frac{12}{6}\) = 2
\(\frac{a_{2}}{a_{1}}=\frac{a_{3}}{a_{2}}\)
కావున ఇవ్వబడిన జాబితా ఒక గుణ శ్రేఢిని అవుతుంది.
దీని సామాన్య నిష్పత్తి r = 2.

(ii) 645, – 32, 16, …………
సాధన.
అన్ని పదాలు శూన్యేతరాలు మరియు
\(\frac{a_{2}}{a_{1}}=\frac{-32}{64}=\frac{-1}{2}\);
\(\frac{a_{3}}{a_{2}}=\frac{16}{-32}=\frac{-1}{2}\);
\(\frac{a_{2}}{a_{1}}=\frac{a_{3}}{a_{2}}=\frac{-1}{2}\)
కావున ఇవ్వబడిన జాబితా ఒక గుణ శ్రేఢిని అవుతుంది.
దీని సామాన్య నిష్పత్తి r = \(\frac{-1}{2}\)

(iii) \(\frac{1}{64}\), \(\frac{1}{32}\), \(\frac{1}{8}\), ………
అన్ని పదాలు శూన్యేతరాలు మరియు
\(\frac{a_{2}}{a_{1}}=\frac{\frac{1}{32}}{\frac{1}{64}}\) = 2;
\(\frac{a_{3}}{a_{2}}=\frac{\frac{1}{8}}{\frac{1}{32}}\) = 4
ఇచ్చట \(\frac{a_{2}}{a_{1}} \neq \frac{a_{3}}{a_{2}}\)
కావున ఇవ్వబడిన సంఖ్యల జాబితా ఒక గుణ శ్రేఢిని ఏర్పరచదు.

ప్రశ్న 22.
\(\frac{5}{2}\), \(\frac{5}{4}\), \(\frac{5}{8}\) …………. గుణశ్రేణి యొక్క 20వ పదమును మరియు n వ పదమును కనుగొనుము. (పేజీ నెం. 154)
సాధన.
ఇచ్చట a = \(\frac{5}{2}\), r = \(\frac{\frac{5}{4}}{\frac{5}{2}}=\frac{5}{4} \times \frac{2}{5}=\frac{1}{2}\)
గుణశ్రేణిలో n వ పదం a_n = ar^{n – 1}
a₂₀ = \(\frac{5}{2}\left(\frac{1}{2}\right)^{19}=\frac{5}{2} \times \frac{1}{2^{19}}=\frac{5}{2^{20}}\)
మరియు n వ పదం
a_n = ar^{n – 1}
= \(\frac{5}{2}\left(\frac{1}{2}\right)^{\mathrm{n}-1}=\frac{5}{2^{\mathrm{n}}}\)

ప్రశ్న 23.
2,272, 4, ….. గుణశ్రేణిలో ఎన్నవ పదము 128 అవుతుంది ? (పేజీ నెం. 154)
సాధన.
a = 2, r = \(\frac{2 \sqrt{2}}{2}\) = √2
లెక్క ప్రకారము n వ పదము = 128
a_n = ar^{n – 1} = 128
(√2)^{n – 1} = \(\frac{128}{4}\) = 64
⇒ 2^{\(\frac{n-1}{2}\)} = 2⁶ భూములు సమానం కావున ఘాతాంకాలు సమానం.
∴ \(\frac{n-1}{2}\) = 6
n – 1 = 12 ⇒ n = 12 + 1 = 13
అనగా 13వ పదము 128 అవుతుంది.

ప్రశ్న 24.
ఒక గుణ శ్రేణిలో 3వ పదము 24 మరియు 6వ పదము 192 అయిన 10వ పదమును కనుగొనుము. (పేజీ నెం. 155)
సాధన.
గుణశ్రేణిలో 3వ పదం a₃ = ar² = 24 …….(1)
6వ పదం a₆ = ar⁵ = 192 ……(2)
(2) ÷ (1)
⇒ \(\frac{a r^{5}}{a r^{2}}=\frac{192}{24}\)
⇒ r³ = 8 = 2³
⇒ r = 2
r విలువను (1) లో రాయగా,
a (2)² = 24
⇒ 4a = 24
⇒ a = 4 = 6
∴ 10వ పదం a₁₀ = ar⁹ = 6(2)⁹
= 6 × 512 = 3072.