SCERT AP 10th Class Maths Textbook Solutions Chapter 2 సమితులు Exercise 2.2 Textbook Exercise Questions and Answers.
AP State Syllabus 10th Class Maths Solutions 2nd Lesson సమితులు Exercise 2.2
ప్రశ్న 1.
A = {1, 2, 3, 4}; B = {1, 2, 3, 5, 6} అయిన A ∩ Bమరియు B ∩ A లను కనుగొనండి. రెండూ సమానమా ?
సాధన.
A = {1, 2, 3, 4}, B = {1, 2, 3, 5, 6}
A ∩ B = {1, 2, 3, 4} ∩ {1, 2, 3, 5, 6}
= {1, 2, 3)
B ∩ A = {1, 2, 3, 5, 6} ∩ {1, 2, 3, 4}
= {1, 2, 3}
∴ A ∩ B = B ∩ A.
![]()
ప్రశ్న 2.
A = {0, 2, 4}, A ∩ Φ మరియు A ∩ A- కనుగొనుము. వ్యాఖ్యానించండి.
సాధన.
A = {0, 2, 4} June 2016, 15
A ∩ Φ = {0, 2, 4} ∩ { } = { }
A ∩ Φ = Φ
ఒక సమితి, శూన్యసమితుల ఛేదనం శూన్యసమితి.
A ∩ A = {0, 2, 4} ∩ {0, 2, 4}
= {0, 2, 4} = A
A ∩ A = A
∴ ఒక సమితి మరియు అదే సమితుల ఛేదనం మళ్ళీ అదే సమితి అవుతుంది.
![]()
ప్రశ్న 3.
A = {2, 4, 6, 8, 10} మరియు B= {3, 6, 9, 12, 15} అయిన A – B మరియు B – A లను కనుగొనుము.
సాధన.
A = {2, 4, 6, 8, 10}; B = {3, 6, 9, 12, 15}
A – B = {2, 4, 6, 8, 10} – {3, 6, 9, 12, 15}
= {2, 4, 8, 10}
B – A = {3, 6, 9, 12, 15} – {2, 4, 6, 8, 10}
= {3, 9, 12, 15}
A – B ≠ B – A.
![]()
ప్రశ్న 4.
A మరియు Bలు రెండు సమితులు, A ⊂ B అయిన A ∪ B ఎంత?
సాధన.
A మరియు B లు రెండు సమితులు. A ⊂ B అయిన A ∪ B = B
ప్రశ్న 5.
A = {x : x ఒక సహజసంఖ్య}
B = {x : x ఒక సరి సహజసంఖ్య}
C = {x : x ఒక బేసి సహజ సంఖ్య}
D = {x : x ఒక ప్రధానసంఖ్య} అయిన క్రింది వాటిని కనుగొనండి.
A ∩ B, A ∩ C, A ∩ D, B ∩ C, B ∩ D, C ∩ D.
సాధన.
A = {x : x ఒక సహజసంఖ్య } = {1, 2, 3, 4, 5, 6, 7,…………}
B = {x : x ఒక సరి సహజసంఖ్య} = {2, 4, 6, ……………..}
C = {x : x ఒక బేసి సహజసంఖ్య } = {1, 3, 5, 7, …………..}
D = {x : x ఒక ప్రధానసంఖ్య } = {2, 3, 5, 7, ………………}
(i) A ∩ B = {1, 2, 3, 4, 5, 6, ……….} ∩ {2, 4, 6, ………….}
= {2, 4, 6, …………….}
A ∩ B = {x : x ఒక సరి సహజసంఖ్య }
(ii) A ∩ C = {1, 2, 3, 4, 5, ………..} ∩ {1, 3, 5, ………}
= {1, 3, 5, ………}
A ∩ C = {x : x ఒక బేసి సహజసంఖ్య }
(iii) A ∩ D = {1, 2, 3, 4, 5, ……….} ∩ {2, 3, 5, 7, ………….}
= {2, 3, 5, 7, …………….}
A ∩ D = {x : x ఒక ప్రధానసంఖ్య}
(iv) B ∩ C = {2, 4, 6, ……} ∩ {1, 3, 5, …….}
= Φ
B ∩ C = Φ
(v) B ∩ D = {2, 4, 6, …………} ∩ {2, 3, 5, 7, ……………}
= {2}
B ∩ D = {x : x ఒక సరి ప్రధానసంఖ్య }
(vi) C ∩ D = {1, 3, 5, 7, 9, 11, ….} ∩{1, 3, 5, 7, 11, ……}
= {3, 5, 7, 11 ………}
C ∩ D = {x: X ఒక బేసి ప్రధానసంఖ్య }
![]()
2వ పద్ధతి :
A = {x : x ఒక సహజసంఖ్య}
B = {x : x ఒక సరి సహజసంఖ్య}
C = {x : x ఒక బేసి సహజసంఖ్య}
D = {x : x ఒక ప్రధానసంఖ్య}
B ⊂ A, C ⊂ A, D ⊂ A మరియు B, C,లు’ వియుక్త సమితులు అవుతాయి కావున,
A ∩ B = B = {x : x ఒక సరి సహజసంఖ్య}
A ∩ C = C = {x : x ఒక బేసి సహజసంఖ్య}
A ∩ D = D = {x : x ఒక ప్రధానసంఖ్య}
B ∩ C = Φ
B ∩ D = {x : x ఒక సరి ప్రధానసంఖ్య} = {2}
C ∩ D = {x : x ఒక బేసి ప్రధానసంఖ్య } = {3, 5, 7, 11, …………..}
![]()
3వ పద్దతి :
A = {x : x ఒక సహజసంఖ్య}
B = {x : x ఒక సరి సహజసంఖ్య }
C = {x : x ఒక బేసి సహజసంఖ్య }
D = {x : x ఒక ప్రధానసంఖ్య}
(i) A ∩ B = {x : x ఒక సహజసంఖ్య మరియు సరి సహజసంఖ్య}
= {x : x ఒక సరి సహజసంఖ్య}
(ii) A ∩ c = {x: x ఒక సహజసంఖ్య మరియు బేసి సహజసంఖ్య}
= {x : x ఒక బేసి సహజసంఖ్య}
(iii) A ∩ D = {x : X ఒక సహజన గఖ్య మరియు ప్రధానసంఖ్య}
= {x : x ఒక ప్రధానసంఖ్య }
(iv) B ∩ C = {x : x ఒక సరి సహజసంఖ్య మరియు బేసి సహజసంఖ్య}.
(v) B ∩ D = {x: X ఒక సరి సంఖ్య మరియు ప్రధాన సంఖ్య }
= {2}
(vi) C ∩ D = {x : x ఒక బేసి సహజసంఖ్య మరియు ప్రధానసంఖ్య}
= {x : x ఒక బేసి ప్రధాన సంఖ్య }
![]()
4వ పద్దతి :
వెన్ చిత్రం ద్వారా సాధించడం. A = {x : x ఒక సహజసంఖ్య}
B = {x: X ఒక సరి సహజసంఖ్య}
C = {x: X ఒక బేసి సహజసంఖ్య}
D = {x : x ఒక ప్రధానసంఖ్య}
B, C, D లు A కి ఉపసమితులు.
కావున A విశ్వసమితి అవుతుంది. ఈ
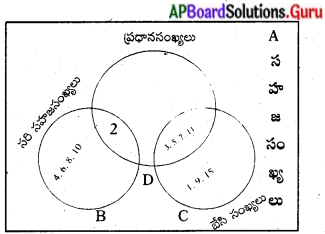
(i) A ∩ B = {2, 4, 6, 8, ……….}
= {x : x ఒక సరి సహజసంఖ్య }
(ii) A ∩ C = {1, 3, 5, 7, 9, ….}
= {x : x ఒక బేసి సహజసంఖ్య }
(iii) A ∩ D = {2, 3, 5, 7, ……….}
= {x : x ఒక ప్రధానసంఖ్య }
(iv) B ∩ C = { } = Φ
(v) B ∩ D = {2}
= {x : x ఒక సరి ప్రధానసంఖ్య }
(vi) C ∩ D = {3, 5, 7, ………}
= {x : x ఒక బేసి ప్రధాన సంఖ్య}
![]()
ప్రశ్న 6.
A = {3, 6, 9, 12, 15, 18, 21};
B = {4, 8, 12, 16, 20};
C = {2, 4, 6, 8, 10, 12, 14, 16};
D = {5, 10, 15, 20} అయిన క్రింది వానిని కనుగొనుము.
(i) A – B
(ii) A – C
(iii) A – D
(iv) B – A
(v) C – A
(vi) D – A
(vii) B – C
(viii) B – D
(ix) C – B
(x) D – B
సాధన.
A = {3, 6, 9, 12, 15, 18, 21}
B = {4, 8, 12, 16, 20}
C = {2, 4, 6, 8, 10, 12, 14, 16}
D = {5, 10, 15, 20}
(i) A – B = {3, 6, 9, 12, 15, 18, 21} – {4, 8, 12, 16, 20}
= {3, 6, 9, 15, 18, 21}
(ii) A – C = {3, 6, 9, 12, 15, 18, 21} – {2, 4, 6, 8, 10, 12, 14, 16}
= {3, 9, 15, 18, 21}
(iii) A – D = {3, 6, 9, 12, 15, 18, 21} – {5, 10, 15, 20}
= {3, 6, 9, 12, 18, 21}
(iv) B- A = {4, 8, 12, 16, 20} – {3, 6, 9, 12, 15, 18, 21}
= {4, 8, 16, 20}
![]()
(v) C – A = {2, 4, 6, 8, 10, 12, 14, 16} – {3, 6, 9, 12, 15, 18, 21}
= {2, 4, 8, 10, 14, 16}
(vi) D – A = {5, 10, 15, 20} – {3, 6, 9, 12, 15, 18, 21}
= {5, 10, 20}
(vii) B – C = {4, 8, 12, 16, 20} – {2, 4, 6, 8, 10, 12, 14, 16}
= {20}
(viii) B – D = {4, 8, 12, 16, 20} – {5, 10, 15, 20}
= {4, 8, 12, 16}
(ix) C – B = {2, 4, 6, 8, 10, 12, 14, 16} – {4, 8, 12, 16, 20}
= {2, 6, 10, 14}
(x) D – B = {5, 10, 15, 20} – {4, 8, 12, 16, 20}
= {5, 10, 15}
![]()
ప్రశ్న 7.
క్రింద ఇవ్వబడిన వాక్యాలు సత్యమా లేక అసత్యమా ? తెలపండి. మీ సమాధానాలను సమర్ధించండి..
(i) {2, 3, 4, 5} మరియు {3, 6} లు వియుక్త సమితులు
(ii) {a, e, i, 0, u} మరియు {a, b, c, d)లు వియుక్త సమితులు.
(iii) {2, 6, 10, 14} మరియు {3, 7, 11, 15} లు వియుక్త సమితులు.
(iv) {2, 6, 10} మరియు {3, 7, 11} లు వియుక్త సమితులు.
సాధన.
(i) {2, 3, 4, 5} మరియు {3, 6} లు వియుక్త సమితులు.
అసత్యం.
రెండు సమితులలో 3 ఉమ్మడి మూలకంగా కలదు. కావున వియుక్త సమితులు కావు.
(ii) {a, e, i, o, u} voBoo {a, b, c, d}.co వియుక్త సమితులు.
అసత్యం.
రెండు సమితులలోను a ఉమ్మడి మూలకంగా కలదు. కావున వియుక్త సమిత, కావు.
(iii) {2, 6, 10, 14} మరియు {3, 7, 11, 15} లు వియుక్త సమితులు.
సత్యం.
రెండు సమితులలో ఉమ్మడి మూలకాలు లేవు. . కావున వియుక్త సమితులు.
(iv) {2, 6, 10} మరియు {3, 7, 11} లు వియుక్త సమితులు. .
సత్యం .
రెండు సమితులలో ఉమ్మడి మూలకాలు లేవు. కావున వియుక్త సమితులు.