SCERT AP 10th Class Maths Textbook Solutions Chapter 12 త్రికోణమితి అనువర్తనాలు Exercise 12.2 Textbook Exercise Questions and Answers.
AP State Syllabus 10th Class Maths Solutions 12th Lesson త్రికోణమితి అనువర్తనాలు Exercise 12.2
ప్రశ్న 1.
ఒక TVటవర్ ఒక రోడ్డు ప్రక్కన నిటారుగా నిలబెట్టబడి ఉంది. రోడ్డుకు అవతలి వైపు నుండి టవర్ పై కొనను పరిశీలించిన 60° ఊర్ధ్వకోణం చేస్తుంది. ఇంకా టవర్ పాదం మరియు ఈ స్థానాన్ని కలిపే సరళరేఖపై 10 మీటర్ల దూరం జరిగిన పిదప టవర్ పై కొన 30° ఊర్థ్వకోణం చేస్తుంది. టవర్ ఎత్తును మరియు రోడ్డు వెడల్పును కనుగొనండి.
సాధన.
పటము నుండి,
AB = TV టవర్ యొక్క ఎత్తు = h మీ. అనుకొనుము.
BD = రోడ్డు వెడల్పు = x మీ. అనుకొనుము.
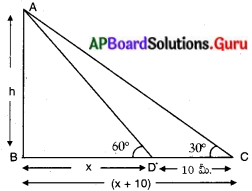
‘D’ మరియు ‘C’ లు పరిశీలన బిందువులు అనుకొనుము.
‘D’ వద్ద టవర్ చేయు ఊర్ధ్వకోణము 60°.
‘C’ మరియు ‘D’ ల మధ్యగల దూరము 10 మీ.
‘C’ వద్ద టవర్ చేయు ఊర్ల్వకోణము 30°.
BC = (x + 10) మీ.
లంబకోణ త్రిభుజము ADB లో,
tan 60° = \(\frac{\mathrm{AB}}{\mathrm{BD}}\)
⇒ √3 = \(\frac{\mathrm{AB}}{\mathrm{x}}\)
⇒ AB = √3x
⇒ h = √3x. ………. (1)
∆ACB నుండి,
tan 30° = \(\frac{\mathrm{AB}}{\mathrm{BC}}\)
⇒ \(\frac{1}{\sqrt{3}}=\frac{A B}{B D+D C}\)
⇒ \(\frac{1}{\sqrt{3}}=\frac{A B}{x+10}\)
⇒ AB = \(\frac{x+10}{\sqrt{3}}\) …………………(2)
AB = √3x ను (2) లో ప్రతిక్షేపించగా,
⇒ √3x = \(\frac{x+10}{\sqrt{3}}\)
⇒ (√3)2x = x + 10
⇒ 3x = x + 10
⇒ 3x – x = 10
⇒ 2x = 10
⇒ x= \(\frac{10}{2}\) = 5 మీ.
⇒ x= 5 మీ.ను సమీకరణము (1) నందు ప్రతిక్షేపించగా,
⇒ AB = √3(5)
⇒ AB = 5√3
∴ టవర్ యొక్క ఎత్తు = 5√3 మీ. ,
రోడ్డు వెడల్పు = 5 మీ.
![]()
ప్రశ్న 2.
1.5 మీటర్ల ఎత్తుగల ఒక బాలుడు 30 మీటర్ల ఎత్తు గల గుడి పై కొనను కొంతదూరము నుండి పరిశీలిస్తున్నాడు. అతడు ఉన్న చోటు నుండి ముందుకు నడిచిన గుడి గోపురం కొన అతని కంటితో చేయు కోణం 300 నుండి 600లకు మారింది. అతడు నడిచిన దూరం ఎంత ?
సాధన.
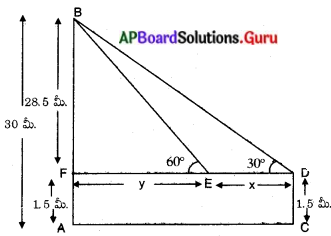
పటం నుండి, AB = గుడి యొక్క ఎత్తు = 30 మీ.
DC = AF = బాలుని ఎత్తు = 1.5 మీ.
‘D’ మొదటి పరిశీలన స్థానము.
‘E’ రెండవ పరిశీలన స్థానము.
DE = x మీ.
ఊర్ధ్వకోణములు ∠BDF = 30° మరియు ∠BEF = 60° అనుకొనుము.
DE = X మరియు EF = y అనుకొనుము.
BF = AB – AF
= 30 – 1.5 = 28.5 మీ.
లంబకోణ త్రిభుజం ∆BDF లో,
tan 30° = \(\frac{\mathrm{BF}}{\mathrm{DF}}\)
⇒ \(\frac{1}{\sqrt{3}}=\frac{28.5}{x+y}\)
⇒ x + y = 28.5√3 ………………(1)
లంబకోణ త్రిభుజం BEF లో,
tan 60° = \(\frac{\mathrm{BE}}{\mathrm{EF}}\)
⇒ √3 = \(\frac{28.5}{y}\)
⇒ y = \(\frac{28.5}{\sqrt{3}}\)
⇒ \(\frac{28.5}{\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}}\)
⇒ y = \(\frac{28.5 \sqrt{3}}{3}\)
⇒ y = 9.5√3
∴ x + 9.5√3 = 28.5√3
∴ x = 28.5√3 – 9.5√4
∴ x = 19√3
= 19 (1.732) = 32.908 మీ.
∴ బాలుడు నడచిన దూరము = 32.908 మీ.
![]()
ప్రశ్న 3.
ఒక విగ్రహం 2 మీటర్ల ఎత్తుగల పీఠంపై నిలబెట్టబడి ఉంది. దానిని కొంత దూరం నుండి పరిశీలించిన విగ్రహం పై భాగం 60° మరియు పీఠంపై భాగం 45° ఊర్ధ్వకోణాలు చేస్తున్నాయి. విగ్రహం ఎత్తు ఎంత ?
సాధన.
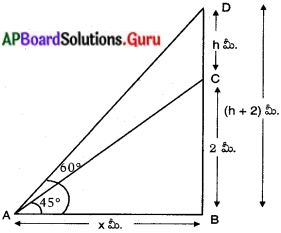
పటము నుండి,
BC = పీఠం ఎత్తు = 2 మీ.
CD = విగ్రహం ఎత్తు = h మీ.
‘A’ పరిశీలన బిందువు.
AB = పీఠంకు, పరిశీలన బిందువుకు మధ్యన గల దూరము = x మీ:
ఊర్ధ్వకోణములు ∠DAB = 60° మరియు ∠CAB = 45.
లంబకోణ త్రిభుజము ∆BAD లో,
tan 60° = \(\frac{\mathrm{BD}}{\mathrm{AB}}\)
⇒ √3 = \(\frac{C D+C B}{x}\)
⇒ √3 = \(\frac{h+2}{\mathbf{x}}\)
⇒ x = \(\frac{h+2}{\sqrt{3}}\) ………………..(1)
లంబకోణ త్రిభుజము CAB లో
tan 45° = \(\frac{\mathrm{BC}}{\mathrm{AB}}\)
⇒ 1 = \(\frac{2}{x}\)
⇒ x = 2
x = 2 ను సమీకరణము (1) లో ప్రతిక్షేపించగా,
⇒ 2 = \(\frac{h+2}{\sqrt{3}}\)
⇒ 2√3 = h + 2
⇒ h = 2√3 – 2
⇒ h = 2(√3 – 1)
⇒ h = 2(1.732 – 1)
⇒ h = 2(0.732)
⇒ h = 1.464 మీ.
∴ విగ్రహం ఎత్తు = 1.464 మీ.
![]()
ప్రశ్న 4.
ఒక భవనం పై నుండి ఒక సెల్ టవర్’ పై భాగాన్ని పరిశీలించిన 60° ఊర్ధ్వకోణం, దాని పాదము 450 నిమ్నకోణం చేస్తుంది. భవనం నుండి టవరకు గల మధ్యదూరం 7 మీటర్లు అయిన టవర్ ఎత్తును కనుగొనండి.
సాధన.
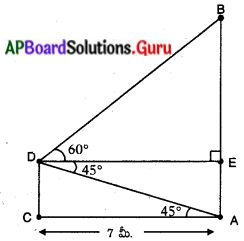
పటం నుండి,
AB = సెల్ టవర్ ఎత్తు
CD = AE = భవనం ఎత్తు భవనం నుండి టవరకు గల మధ్య దూరం = 7 మీ.
ఊర్థ్వకోణములు ∠BDE = 60° మరియు ∠EDA = ∠DAC= 45°
DE = AC = 7 మీ.
∆BDE నుండి,
tan 60° = \(\frac{\mathrm{BE}}{\mathrm{DE}}\)
⇒ √3 = \(\frac{\mathrm{BE}}{7}\)
⇒ BE = 7√3 ……………. (1)
లంబకోణ త్రిభుజం ADC నుండి,
tan 45° = \(\frac{\mathrm{CD}}{\mathrm{AC}}\)
⇒ 1 = \(\frac{\mathrm{CD}}{7}\)
⇒ CD = 7 ……………… (2)
(1), (2) ల నుండి, టవర్ ఎత్తు = AB = AE + BE
= 7 + 7√3 = 7(1 + √3)
= 7(1 + 1.732) = 7(2.732) = 19.124 మీ.
∴ టవర్ యొక్క ఎత్తు = 19.124 మీ.
![]()
ప్రశ్న 5.
భూమితో 300ల ఊర్థ్వకోణం చేస్తూ 18 మీటర్ల పొడవున్న ఒక ధృడమైన లోహపు తీగ ఆధారంగా ఒక . విద్యుత్ స్థంభం నిలబెట్టబడి ఉంది. తీగపొడవు చాలా ఎక్కువ ఉన్న కారణంగా తీగలో కొంత భాగం కత్తిరించి, మిగిలిన దానిని భూమితో 60° కోణం చేస్తూ అమర్చబడింది. తీగలో కత్తిరించగా మిగిలిన తీగపొడవు ఎంత ?
సాధన.
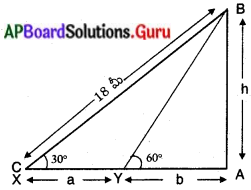
పటంలో,
AB = విద్యుత్తు స్థంభం ఎత్తు = h మీ.
BC = లోహపు తీగ అసలు పొడవు = 18 మీ.
X మరియు Yలు మొదటి మరియు రెండవ పరిశీలన స్థానములు.
AX = a + b మరియు AY = b అనుకొనుము.
ఊర్ధ్వకోణములు ∠BXA = 30° మరియు ∠BYA = 60°.
∆BAX నుండి,
sin 30° = \(\frac{\mathrm{AB}}{\mathrm{BC}}\)
⇒ \(\frac{1}{2}=\frac{h}{18}\)
⇒ h = \(\frac{18}{2}\) = 9
∆ABY నుండి,
tan60° = \(\frac{\mathrm{AB}}{\mathrm{BY}}\)
⇒ √3 = \(\frac{h}{b}\)
⇒ b = \(\frac{\mathrm{h}}{\sqrt{3}}\)
⇒ b = \(\frac{9}{\sqrt{3}}\) (1) నుండి)
∆ABY నుండి,
cos60° = \(\frac{A Y}{B Y}\)
\(\frac{1}{2}=\frac{b}{B Y}\)
⇒ BY = \(\frac{9}{\sqrt{3}} \times 2=\frac{18}{\sqrt{3}}\)
⇒ BY = \(\frac{18}{\sqrt{3}}\)
BY = 10.39261
∴ తీగను కత్తిరించగా మిగిలిన తీగపొడవు = BC – BY = 18 – 10.39261 = 7.608 మీ.
![]()
ప్రశ్న 6.
ఒక టవర్ అడుగుభాగం నుండి భవనం పై భాగం 30° ఊర్ధ్వకోణం చేస్తుంది. భవనం అడుగుభాగం నుండి టవర్ పై భాగం 60° ఊర్థ్వకోణం చేస్తుంది. టవర్ ఎత్తు 30 మీటర్లు అయిన, భవనం ఎత్తు కనుగొనుము.
సాధన.
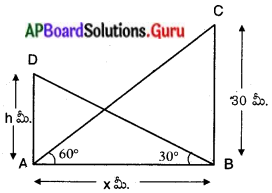
పటం నుండి,
BC = టవర్ యొక్క ఎత్తు = 30 మీ.
AD = భవనం ఎత్తు = 7 మీ.
టవర్ అడుగు భాగం నుండి భవనం పై భాగం చేయు ఊర్థ్వకోణం = ∠BAC = 60°
భవనం అడుగుభాగం నుండి టవర్ పై భాగం చేయు ఊర్ధ్వకోణము = ∠ABD = 30°
భవనంకు, టవరకు మధ్యన గల దూరము = AB = x మీ.
∆ABD లో,
tan 30° = \(\frac{\mathrm{AD}}{\mathrm{AB}}\)
⇒ \(\frac{1}{\sqrt{3}}=\frac{h}{x}\)
h = \(\frac{x}{\sqrt{3}}\) ………… (1)
∆BAC నుండి,
tan 60° = \(\frac{\mathrm{BC}}{\mathrm{AB}}\)
⇒ √3 = \(\frac{30}{x}\)
⇒ x = \(\frac{30}{\sqrt{3}}\)
సమీకరణం (1) లో x విలువను ప్రతిక్షేపించగా,
⇒ h = \(\frac{30}{\sqrt{3}} \times \frac{1}{\sqrt{3}}=\frac{30}{3}\) = 10 మీ.
∴ భవనం ఎత్తు h = 10 మీ.
![]()
ప్రశ్న 7.
120 అడుగుల వెడల్పైన రోడ్డుకు ఇరువైపుల సమాన ఎత్తు కలిగిన రెండు స్తంభాలు నిలబెట్టబడి ఉన్నాయి. వాటి మధ్యలో ఉన్న రోడ్డుపై ఒక బిందువు నుండి వాటి పై భాగాలను పరిశీలించిన అవి 60° మరియు 30° ఊర్థ్వకోణాలు చేస్తున్నాయి. అయిన ఆ స్థంభాల ఎత్తు కనుగొనుము మరియు ప్రతి స్తంభము అడుగుభాగం నుండి బిందువుకు గల దూరమును కనుగొనుము.
సాధన.
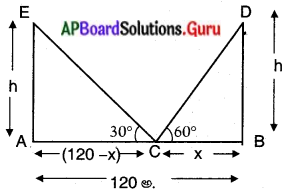
పటం నుండి,
AB = రోడ్డు వెడల్పు = 120 అడుగులు.
AE = BD = సమాన ఎత్తులు గల రెండు స్థంభాలు = 4 మీ.
‘C’ పరిశీలన బిందువు.
ఊర్థ్వకోణములు ∠BCD = 60° మరియు ∠ACE = 30°
BC = x అయిన AC = AB – BC = (120 – X) మీ.
∆ACE లో,
tan 30° = \(\frac{\mathrm{AE}}{\mathrm{AC}}\)
⇒ \(\frac{1}{\sqrt{3}}=\frac{h}{120-x}\)
⇒ h√3 = 120 – x
⇒ h√3 + x = 120 ………………….(1)
∆BCD లో,
tan 60° = \(\frac{\mathrm{BD}}{\mathrm{BC}}\)
⇒ √3 = \(\frac{\mathrm{h}}{\mathrm{x}}\)
⇒ h = √3x …………….. (2)
h = √3x ను సమీకరణం (1) నందు ప్రతిక్షేపించగా,
⇒ (√3x) √3 + x = 120
⇒ 3x + x = 120
⇒ 4x = 120
⇒ x = \(\frac{120}{4}\) = 30 అడుగులు
మొదటి స్థంభం నుండి పరిశీలన బిందువుకు గల దూరం. (x) = 30 మీ.
⇒ x = 30 ను సమీకరణం (2) నందు ప్రతిక్షేపించగా,
⇒ h = 30√3 = 30 (1.732) = 51.96
∴ h = 51.96 మీ.
![]()
ప్రశ్న 8.
టవర్ తో ఒకే సరళరేఖపై ఉండే 4 మీటర్లు మరియు 9 మీటర్ల దూరంలో నున్న రెండు బిందువుల నుండి టవర్ కొనను పరిశీలించిన చేసే ఊర్ద్వకోణాలు పూరకాలు. టవర్ ఎత్తును కనుగొనండి.
సాధన.
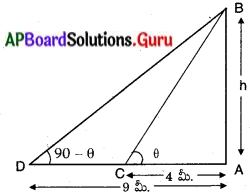
పటం నుండి,
AB = టవర్ యొక్క ఎత్తు = h మీ.
‘C’ మరియు ‘D’ లు భూమిపై రెండు పరిశీలన బిందువులు.
AC = 4 మీ. = మొదటి పరిశీలన స్థానం నుండి టవరకు గల దూరము.
AD = 9 మీ. = రెండవ పరిశీలన స్థానం నుండి టవరకు గల దూరము.
ఊర్థ్వకోణాలు ∠ACB = θ మరియు ∠ADB = 90° – θ అనుకొనుము.
లంబకోణ త్రిభుజం ABC లో,
tan θ = \(\frac{\mathrm{AB}}{\mathrm{AC}}\)
tan θ = \(\frac{h}{4}\) ……….. (1)
∆ABD నుండి,
tan (90 – θ) = \(\frac{\mathrm{AB}}{\mathrm{AD}}\)
⇒ cot θ = \(\frac{\mathrm{h}}{9}\)
⇒ \(\frac{1}{\tan \theta}=\frac{h}{9}\)
⇒ tan θ = \(\frac{9}{h}\) ………………………… (2)
(1), (2) ల నుండి,
\(\frac{h}{4}=\frac{9}{h}\)
⇒ h2 = 36 (అడ్డ గుణకారము చేయగా)
⇒ h = √36 = 6 మీ.
∴ టవర్ యొక్క ఎత్తు = 6 మీ.
ప్రశ్న 9.
భూమిపై నున్న A బిందువు నుండి ఒక జెట్ విమానాన్ని పరిశీలిస్తే 60° ఊర్ధ్వకోణం చేస్తుంది. 15 సెకన్ల తర్వాత దాని ఊర్థ్వకోణం 309గా మారుతుంది. ఆ జెట్ విమానం 1500√3 మీటర్ల స్థిర ఎత్తులో ఎగురుతూ ఉంటే దాని వేగాన్ని కనుక్కోండి. (√3 = 1.732)
సాధన.
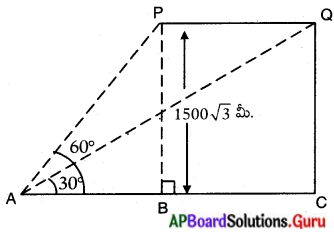
పటం నుండి,
P మరియు Qలు విమానం యొక్క రెండు స్థానములు.
‘A’ పరిశీలన బిందువు.
ABC అనునది ‘A’ గుండా పోవు ఒక క్షితిజ సమాంతర రేఖ.
‘A’ నుండి P మరియు Q ల యొక్క ఊర్థ్వకోణాలు వరుసగా 60° మరియు 30°.
∴ ∠PAB = 60°, ∠QAC = 30°.
జెట్ విమానపు స్థిర ఎత్తు = 1500√3 మీటర్లు.
∆ABP లో,
tan 60° = \(\frac{\mathrm{BP}}{\mathrm{AB}}\)
⇒ √3 = \(\frac{1500 \sqrt{3}}{\mathrm{AB}}\)
⇒ AB = \(\frac{1500 \sqrt{3}}{\sqrt{3}}\)
= 1500 మీ.
∆ACQ లో,
tan 30° = \(\frac{\mathrm{CQ}}{\mathrm{AC}}\)
⇒ \(\frac{1}{\sqrt{3}}=\frac{1500 \sqrt{3}}{\mathrm{AC}}\)
⇒ AC = 1500 √3 × √3
⇒ AC = 1500 × 3 = 4500మీ.
పటం నుండి, PQ = BC = AC – AB
= 4500 – 1500 = 3000 మీటర్లు
ఆ విమానం 15 సెకన్లలో 3000 మీటర్లు ప్రయాణించినది.
∴ విమానపు వేగము = \(\frac{3000}{15}\) = 200 మీ/సె.