AP Board 10th Class Maths Solutions Chapter 1 వాస్తవ సంఖ్యలు Ex 1.2

SCERT AP 10th Class Maths Textbook Solutions Chapter 1 పూర్ణ సంఖ్యలు Ex 1.2 Textbook Exercise Questions and Answers.

AP State Syllabus 10th Class Maths Solutions 1st Lesson వాస్తవ సంఖ్యలు Exercise 1.2

ప్రశ్న1.
కింది వానిలో ప్రతిసంఖ్యను ప్రధాన కారణాంకాల లబ్ధంగా రాయండి.
(i) 140
(ii) 156
(iii) 3825
(iv) 5005
(v) 7429
సాధన:
(i) 140

140 = 2 × 2 × 5 × 7
= 2² × 5 × 7

(ii) 156

156 = 2 × 2 × 3 × 13
= 2² × 3 × 13

(iii) 3825

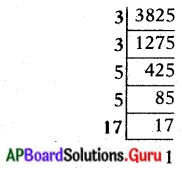
3825 = 3 × 3 × 5 × 5 × 17
= 3² × 5² × 17

(iv) 5005

5005 = 5 × 7 × 11 × 13

(v) 7429

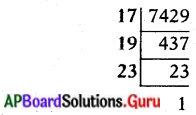
7429 = 17 × 19 × 23

ప్రశ్న2.
కింది పూర్ణసంఖ్యల యొక్క క.సా.గు మరియు గ.సా.కా లను ప్రధాన కారణాంకాల లబ్ధ పద్ధతిలో కనుగొనండి.
(i) 12, 15 మరియు 21
(ii) 17, 23 మరియు 29
(iii) 8, 9 మరియు 25
(iv) 72 మరియు 108
(v) 306 మరియు 657
సాధన.
(i) 12, 15 మరియు 21
12 = 22 × 3; 15 = 3 × 5; 21 = 3 × 7
∴ 12, 15 మరియు 21 ల క.సా.గు = 2² × 3 × 5 × 7 = 420
∴12, 15 మరియు 21ల గ.సా.భా = 3
(సంఖ్యల యొక్క ప్రధాన కారణాంకాల లబ్దంలో అన్ని కారణాంకాల గరిష్ఠ ఘాతాంకం గల కారణాంకాల లబ్ధము గ.సా.భా)
(సంఖ్యల యొక్క ప్రధాన కారణాంకాల లబ్ధంలో కనిష్ఠ ఘాతాంకం గల సామాన్య కారణాంకాల లబ్దము క.సా.గు)

(ii) 17, 23 మరియు 29
17, 23 మరియు 29 లు ప్రధాన సంఖ్యలు.
∴ క.సా.గు = 17 × 23 × 29 = 11339
∴ గ.సా.భా = 1
(17, 23 మరియు 29 లు సాపేక్ష ప్రధాన సంఖ్యలు)

(iii) 8, 9 మరియు 25
8 = 2³; 9 = 3²; 25 = 5²
∴ 8, 9, 25 ల క.సా.గు = 2³ × 3² × 5²
= 8 × 9 × 25
= 1800
8, 9, 25 లు సాపేక్ష ప్రధాన సంఖ్యలు –
∴ గ.సా.భా = 1

(iv) 72 మరియు 108

72 = 2³ × 3² ;
108 = 2² × 3³
∴ 72, 108 ల క.సా.గు = 2³ × 3³
= 8 × 27 = 216
∴ గ.సా.భా = 2² × 3² = 4 × 9 = 36

v) 306 మరియు 657

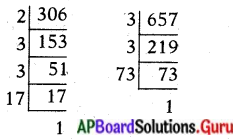
306 = 2 × 3² × 17
657 = 3² × 73
306, 657 ల క.సా.గు = 2 × 3² × 17 × 73
=2 × 9 × 17 × 73
= 22338
గ.సా.భా = 3² = 9

ప్రశ్న3.
n ఒక సహజ సంఖ్య అయిన 6″ సంఖ్య ‘సున్న’తో అంతమగునో, కాదో సరిచూడండి.
సాధన.
6ⁿ = (2 × 3)ⁿ = 2ⁿ × 3ⁿ
6ⁿ = 2ⁿ × 3ⁿ
సహజసంఖ్య n ఏ విలువకైనా’ 6ⁿ యొక్క ప్రధాన కారణాంకాల లబ్ధంలో 5 కారణాంకంగా లేదు.
కావున 6ⁿ సంఖ్య ఒకట్ల స్థానంలో సున్న లేదా 5 ఉండదు.
∴ 6ⁿ సంఖ్య సున్నతో అంతం కాదు.

ప్రశ్న4.
1 × 11 × 13 + 13 మరియు 7 × 6 × 5 × 4 × 3 × 2 × 1 + 5 ఏవిధంగా సంయుక్త సంఖ్యలగునో వివరించండి.
సాధన.
(i) 7 × 11 × 13 + 13 = 13(7 × 11 + 1)
= 13(77 + 1)
= 13 × 78
7 × 11 × 13 + 13కు 13 మరియు 78లు కారణాంకాలు కావున 7 × 11 × 13 + 13 సంయుక్త సంఖ్య అవుతుంది.

(ii) 7 × 6 × 5 × 4 × 3 × 2 × 1 + 5
= 5 (7 × 6 × 4 × 3 × 2 × 1 + 1)
= 5 × (1008 + 1)
= 5 × 1009
7 × 6 × 5 × 4 × 3 × 2 × 1 + 5కు 5 మరియు 1009లు.
కారణాంకాలు కావున 7 × 6 × 5 × 4 × 3 × 2 × 1 + 5 సంయుక్త సంఖ్య అవుతుంది.

ప్రశ్న5.
(17 × 11 × 2) + (17 × 11 × 5) అనేది ఒక సంయుక్త సంఖ్య’ అని ఏవిధంగా నిరూపిస్తావు ? వివరించండి.
సాధన.
(17 × 11 × 2) + (17 × 11 × 5)
= (17 × 11) (2 + 5) = 17 × 11 × 7
= 187 × 7
(17 × 11 × 2) + (17 × 11 × 5) యొక్క కారణాంకాలు 17, 11 మరియు 7.
కావున ఇది సంయుక్త సంఖ్య అవుతుంది:

ప్రశ్న6.
6¹⁰⁰ యొక్క ఫలిత సంఖ్యలో ఒకట్ల స్థానంలోని అంకె ఏది ?
సాధన:
6¹ = 6 మరియు 6² = 36, 6³ = 216; అలాగే
6⁴ = 1296 తదుపరి 6⁵ = 1296 × 6 = 7776
ఈ విధంగా 6ను ఏ ఘాతాన్ని పెంచినప్పటికి దాని ఒకట్ల స్థానంలో ‘6’ మాత్రమే ఉండుట మనం గమనించవచ్చు.
∴ 6¹⁰⁰ యొక్క ఒకట్ల స్థానంలో గల అంకె = 6.