SCERT AP 10th Class Maths Textbook Solutions Chapter 1 పూర్ణ సంఖ్యలు Ex 1.1 Textbook Exercise Questions and Answers.
AP State Syllabus 10th Class Maths Solutions 1st Lesson వాస్తవ సంఖ్యలు Exercise 1.1
ప్రశ్న1.
యూక్లిడ్ భాగహార శేష విధి ఆధారంగా క్రింది జతల గ.సా.భాను కనుగొనండి.
(i) 900 మరియు 270
సాధన:
a = 900, b = 270 వీటిని .
a = bq + r రూపంలో వ్రాయగా
900 = 270(3) + 90;
270 = 90(3) + 0
కావున 900, 270ల గ.సా.భా = 90
రెండవ పద్ధతి :
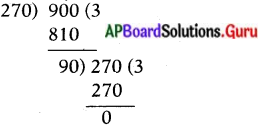
∴ గ.సా.భా = 90.
![]()
(ii) 196 మరియు 38220
సాధన:
a = 38220; b = 196 అనుకొనుము
a = bq + r రూపంలో వ్రాయగా,
38220 = 196(195) + 0
కావున (∴ శేషం = 0) 196, 38220 ల గ.సా.భా = 196.
రెండవ పద్ధతి:

∴ 196, 38220 ల గ.సా.భా = 196
(iii) 1651 మరియు 2032
సాధన:
1651 మరియు 2032 ల గ.సా.భా
a = 2032, మరియు b = 1651 వీటిని
a = bq + r రూపంలో, వ్రాయగా
2032 = 1651(1) + 381
1651 = 381(4) + 127
381 = 127(3) + 0
∴ 1651 మరియు 2032 ల గ.సా.భా = 127
రెండవ పద్ధతి :

∴ 1651, 2032 ల గ.సా.భా = 127
![]()
ప్రశ్న2.
q ఏదైనా ఒక పూర్ణ సంఖ్య అయినప్పుడు ప్రతి ధన బేసి పూర్ణ సంఖ్య 6q+ 1 లేదా 6q + 3 లేదా 6q+ 5 రూపంలో ఉంటుందని చూపుము.
సాధన:
a ఏదైనా ఒక ధన బేసి పూర్ణ సంఖ్య అనుకుందాం. భాగాహార శేష విధిని a మరియు b = 6 పై అనువర్తింపగా 0 ≤ r < 6, కావున శేషం 0 లేదా 1 లేదా 2 లేదా 3 లేదా 4 లేదా 5 అగును. వీటి ఆధారంగా ణ విలువలు వరుసగా
a = 6q + 0 లేదా
= 6q + 1 లేదా
= 6q + 2 లేదా
= 6q + 3 లేదా
= 6q + 4 లేదా
= 6q + 5 అగును.
పై వాటిలో a = 6q+ 0, a = 6q + 2, a = 6q + 4 లు 2 చే నిశ్శేషంగా భాగింపబడును. కావున అవి సరి సంఖ్యలు.
కాగా మిగిలినవి a = 6q + 1
a = 6q+ 3
a = 6q + 5 లు 2 చే నిశ్శేషంగా భాగింపబడవు. కావున అవి సరిసంఖ్యలు కాలేవు. అందుచే అవి ఖచ్చితంగా ధన బేసి పూర్ణసంఖ్యలు అవుతాయి.
![]()
ప్రశ్న3.
ఏదైనా ధన పూర్ణసంఖ్య యొక్క వర్గం 3p లేదా 3p + 1 రూపంలో ఉంటుందని యూక్లిడ్ భాగహార శేష విధి ఆధారంగా చూపుము.
సాధన:
‘a’ అనునది ఏదైనా ధన పూర్ణ సంఖ్య అనుకొనుము. మరియు b = 3 అనుకుందాం.
యూక్లిడ్ భాగహార శేష న్యాయం ప్రకారం a = bq + r ఇచ్చట b = 3 కావున r = 0 లేదా 1 లేదా 2 అగును.
∴ a = 3q + 0 లేదా a = 3q + 1 లేదా a = 3q + 2
∴ a = 3q అయిన a2 = 9q2 = 3(3q7)
= 32 రూపం a = 3q + 1 అయిన
a2 = (3q + 1)2 = 9q2 + 6q + 1
= 3[3q2 + 2q] + 1
= 3p+ 1 రూపం
a = 3q + 2 అయిన a2
= (3q + 2)2
= 9q2 + 12q + 4
= 3[3q2 + 4q + 1] + 1
= 3p + 1 రూపం
కావున ఒక ధన పూర్ణ సంఖ్య యొక్క వర్గం 3p లేదా 3p+ 1 రూపంలో ఉండును.
![]()
ప్రశ్న4.
ఏదైనా ధన పూర్ణ సంఖ్య యొక్క ఘనం 9m లేదా 9m + 1 లేదా 9m + 8 రూపంలో ఉంటుందని చూపుము.
సాధన:
‘a’ అనునది ఏదేని ఒక ధన పూర్ణసంఖ్య మరియు b = 3.అనుకుందాం.
యూక్లిడ్ భాగహార శేష న్యాయం ప్రకారం
a = 3q + r ………… (1)
ఇక్కడ q 6 W మరియు 0 ≤ r < 2 అనగా r = 0 లేదా r = 1 లేదా r = 2
సందర్భం : 1
r = 0
(1) ⇒ a = 34
a3 = (3q)3
= 27q3
= 9 (3q3) = 9 m
ఇక్కడ m = 3q3.
సందర్భం : 2, r = 1
(1) ⇒ a = 3q + 1
a3 = (3q + 1)3
= 27q3 + 27q2 + 9q + 1
= 9(3q3 + 3q2 + q) + 1
= 9 m + 1 ఇక్కడ m = 3q3 + 3q2 + q
సందర్భం : 3
r = 2 (1) = a = (3q + 2)3
= 27q3 + 54q2 + 36q+ 8 = 9(3q3 + 6q2 + 44) + 8
= 9m + 8 ఇక్కడ m= 3q + 6q2 + 4q .. కావున ధన పూర్ణసంఖ్య యొక్క ఘనము 9m లేదా 9m + 1 లేదా 9m + 8 రూపంలో ఉంటుంది.
![]()
రెండవ పద్ధతి :
a అనునది ఏదేని ధనపూర్ణ సంఖ్య మరియు b = 3 అనుకొనుము.
యూక్లిడ్ భాగహార శేష న్యాయం ప్రకారం.
a = 3q + r, q ∈ W, 0 ≤ r < 3
⇒ a3 = (3q + r)3
⇒ a3 = 27q2 + 27q2r + 9qr2 + r ………… (1)
సందర్భం : 1, r = 0
(1) ⇒ a3 = 27q3 = 9(3q3) = 9m
ఇక్కడ m = 3q3
సందర్భం : 2,
r = 1
(1) ⇒ a3 = 27q3 + 27q2 + 9q + 1
= 9(3q3 + 3q2 + 4) + 1
a3 = 9m + 1 ఇక్కడ m = 3q3 + 3q2 + q
సందర్భం : 3,
r = 2
(1) ⇒ a3 = 27q3 + 54q2 + 36q + 8
= 9(3q3 + 6q2 + 4q) + 8
a3 = 9m + 8
ఇక్కడ m = 3q3 + 6q2 + 4q
కావున ధనపూర్ణ సంఖ్య యొక్క ఘనం 9m లేదా 9m + 1 లేదా 9m + 8 రూపంలో ఉంటుంది.
![]()
ప్రశ్న5.
ఏదైన ధన పూర్ణ సంఖ్య n కు n, n + 2 లేదా n + 4 లలో ఏదైనా ఒకటి మాత్రమే 3 చే భాగింపబడుతుందని చూపుము.
(లేదా)
a ధన పూర్ణ సంఖ్య అయిన a, a + 2 మరియు a + 4 లలొ ఏదో ఒకటి మాత్రమే 3 చే భాగింపబడుతుందని చూపుము.
సాధన.
n ఏదేని ధనపూర్ణ సంఖ్య మరియు n ను 3 చే భాగించగా భాగఫలం q, శేషం / అనుకుందాం.
యూక్లిడ్ భాగహార శేషన్యాయం ప్రకారం. n = 3q + r – (1), 0 ≤ r < 3, r = 0 లేదా 1 లేదా 2
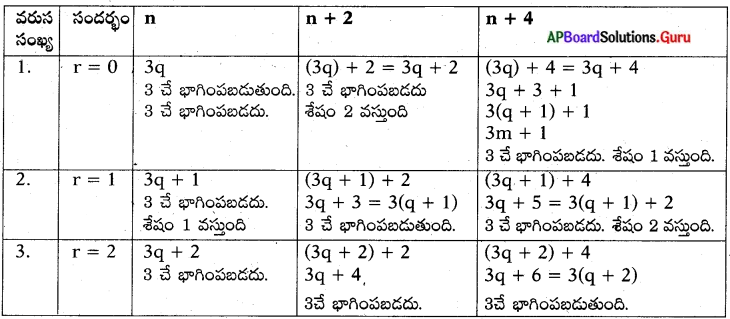
పై మూడు సందర్భాల నుండి ఏదేని ధనపూర్ణ సంఖ్య n కు n n + 2 లేదా n + 4 లలో ఏదైనా ఒకటి మాత్రమే 3చే భాగింపబడుతుంది.