AP 6th Class Social Bits Chapter 3 Maps with Answers

Practice the AP 6th Class Social Bits with Answers Chapter 3 Maps on a regular basis so that you can attempt exams with utmost confidence.

AP State Syllabus 6th Class Social Bits 3rd Lesson Maps with Answers

Choose the correct answer.

Question 1.
Most of the maps contain an arrow marked with the letter
A) N
B) S
C) E
D) W
Answer:
A) N

Question 2.
If we stand facing east, all the things to our left are towards
A) South
B) North
C) West
D) South East
Answer:
B) North

Question 3.
If we stand facing east, all the things to our right are towards
A) South
B) North
C) West
D) North West
Answer:
A) South

Question 4.
If we stand facing east, all the things behind us are towards.
A) South
B) North
C) West
D) None
Answer:
C) West

Question 5.
The largest continent in the world
A) Africa
B) North America
C) Asia
D) North East
Answer:
C) Asia

Question 6.
Large water bodies are called.
A) Rivers
B) Oceans
C) Lakes
D) Mountains
Answer:
B) Oceans

Question 7.
Maps showing the distribution of population conditions are called
A) Population maps
B) Political maps
C) Physical maps
D) None of these
Answer:
A) Population maps

Question 8.
Usually, maps are prepared in such a manner that North is at the ……….. of the map.
A) top
B) bottom
C) right-hand side
D) left-hand side
Answer:
A) top

Question 9.
This is used to indicate distance on the map.
A) symbol
B) direction
C) scale
D) none
Answer:
C) scale

Question 10.
The scale is the …………… of distance between two points on the map to the actual distance on the ground.
A) ratio
B) axis
C) both (A) and (B)
D) none
Answer:
A) ratio

Study the map to find out how to use the symbols:

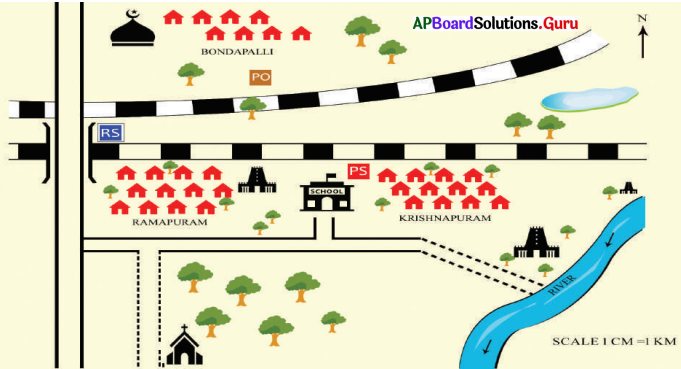
Question 1.
The symbol indicates.
A) Railway line
B) National highway
C) Pucca road
D) State highway
Answer:
A) Railway line

Question 2.
The symbol indicates
A) House
B) Temple
C) Trees
D) Church
Answer:
C) Trees

Question 3.
The symbol indicates.
A) Church
B) Masjid
D) Gurudwara
C) Temple
Answer:
B) Masjid

Question 4.
The symbol indicates.
A) Kutcha road
B) National highway
D) Railway line
C) Pucca road
Answer:
A) Kutcha road

Question 5.
The symbol indicates.
A) House
B) Temple
C) Church
D) Masjid
Answer:
A) House

Question 6.
Map that shows cities, states, countries is
A) Political Map
B) Physical Map
C) Thematic Map
D) States Map
Answer:
A) Political Map

Question 7.
Among the following one country does not share a boundary with India.
A) Bhutan
B) Afghanistan
C) Pakistan
D) USA
Answer:
D) USA

Read the figure and answer 8 to 10 questions.

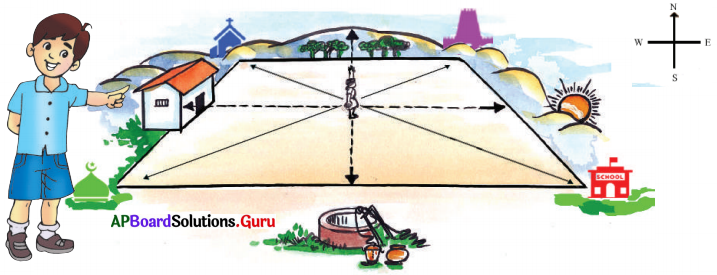
Question 8.
In the above picture well is in which direction?
A) North
B) South
C) East
D) West
Answer:
B) South

Question 9.
School is situated in which direction?
A) North-West
B) South-East
C) North-East
D) South-West
Answer:
B) South-East

Question 10.
Masjid is located in which direction.
A) North-West
B) South-East
C) North-East
D) South-West
Answer:
D) South-West

Question 11.
In a map blue color is used to indicate
A) Sky
B) Greenary
C) Trees
D) Water
Answer:
D) Water

Question 12.
To show plateaus which color is used in maps?
A) Yellow
B) Blue
C ) Brown
D) Green
Answer:
A) Yellow

Observe the map showing continents and oceans (13-14).

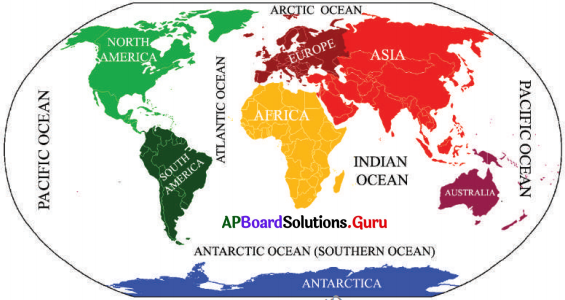
Question 13.
What is the ocean on both sides of the map?
A) the Arctic Ocean
B) Antarctic Ocean
C) the Indian Ocean
D) the Pacific Ocean
Answer:
D) Pacific Oceans

Question 14.
What is the country South to North America?
A) Europe
B) Africa
C) Australia
D) South America
Answer:
D) South America

Question 15.
Which statement is correct?
A: Physical maps show mountains, plateaus, plains, oceans.
B: Political maps show villages, cities, districts, states, and countries.
A) A is correct
B) B is correct
C) Both A and B are correct
D) Both A and B are wrong
Answer:
C) Both A and B are correct

Question 16.
A: Thematic map shows the distribution of specific features.
B: Sri Lanka shares land boundaries with India.
A) A is correct
B) B is correct
C) Both A and B are correct
D) Both A and B are wrong
Answer:
A) A is correct

Question 17.
A: Large-scale maps represent large areas.
B: Small-scale maps represent small areas.
A) A is correct
B) B is correct
C) Both A and B are correct
D) Both A and B are wrong
Answer:
D) Both A and B are wrong

Fill in the blanks.

1. Rough drawing is drawn without scale and direction ………………….
Answer:
sketch

2. Colors in the physical map represent differently………………….
Answer:
physical features

3. Blue color in the physical maps represent ………………….
Answer:
water

4. Green color in the physical maps represent ………………….
Answer:
plains or low lands

5. Yellow color in the physical maps represent ………………….
Answer:
plateaus

6. Brown color in the physical maps represent ………………….
Answer:
mountains

7. Cartographers are ………………….
Answer:
map makers

8. Collection of maps is called an ………………….
Answer:
atlas

9. Largest continent in the world is ………………….
Answer:
Asia

10. Land masses on the globe are called ………………….
Answer:
Continents

11. Oceans are ………………….
Answer:
large water bodies