AP 10th Class Maths Bits Chapter 5 Quadratic Equations with Answers

Practice the AP 10th Class Maths Bits with Answers Chapter 5 Quadratic Equations on a regular basis so that you can attempt exams with utmost confidence.

AP State Syllabus 10th Class Maths Bits 5th Lesson Quadratic Equations with Answers

Question 1.
If sin α, cos α are roots of the equation ax2 + bx + c = 0, then ………………
A) a² + b² – 2ac = 0
B) (a + c)² = b² + c²
C) a² – b² + 2ac = 0
D) (a + c)² = b² – c²
Answer:
D) (a + c)² = b² – c²

Question 2.
If px² + qx + r = 0 has equal roots , then r = ……………….
A) \(\frac{\mathrm{q}^{2}}{2 \mathrm{p}}\)
B) \(\frac{\mathrm{q}}{2 \mathrm{p}}\)
C) \(\frac{-q^{2}}{4 p}\)
D) \(\frac{q^{2}}{4 p}\)
Answer:
D) \(\frac{q^{2}}{4 p}\)

Question 3.
If the equations x² + bx + c = 0, x² + cx + b = 0 [b ≠ c] have a common root, then …………………
A) b + c = 0
B) b + c = 1
C) b + c + 1 = 0
D) None of these
Answer:
C) b + c + 1 = 0

Question 4.
The roots of x – \(\frac{3}{x}\) = 2 are
A) 3, 2
B) 3,-2
C) 3, 1
D) 3, – 1
Answer:
D) 3, – 1

Question 5.
The roots of the quadratic equation 2x² -2√2x + 1 = 0 are ……………….
A) √2, \(\frac{1}{\sqrt{2}}\)
B) \(\frac{1}{2}, \frac{1}{2}\)
C) \(\frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}}\)
D) √2, √2
Answer:
C) \(\frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}}\)

Question 6.
If α, β are the roots of x² + 2x + 5 = 0 then \(\frac{\alpha}{\beta}+\frac{\beta}{\alpha}\) =
A) \(\frac{6}{5}\)
B) \(\frac{4}{5}\)
C) \(-\frac{6}{5}\)
D) \(-\frac{4}{5}\)
Answer:
C) \(-\frac{6}{5}\)

Question 7.
If the roots of a(b – c)x² + b(c – a) x + c(a – b) = 0 are equal, then a, b, c are in
A) AP
B) GP
C) HP
D) None
Answer:
C) HP

Question 8.
The roots of are \(\frac{1}{x+4}-\frac{1}{x-7}=\frac{11}{30}\)
A) -1, 2
B) 1, 2
C) 1, -2
D) -1, -2
Answer:
B) 1, 2

Question 9.
If A is the solution set of x² – 5x + 6 = 0 and B is the solution set of x – \(\sqrt{3 x-6}=\) = 2, then A ∩ B =
A) Φ
B) A
C) B
D) {2}
Answer:
D) {2}

Question 10.
If the sum of the squares of the roots of x² + px – 3 = 0 is 10, then p =
A) ± 2
B) ± 3
C) ± 5
D) ± 6
Answer:
A) ± 2

Question 11.
If one root of x² – 8x + 13 = 0 is 4 + √3,then the other root is …………….
A) 2 + √3
B) 2 – √3
C) -4 + √3
D) 4 – √3
Answer:
D) 4 – √3

Question 12.
If α and β are the roots of a quadratic a P equation x² – px + q = 0, then \(\frac{\alpha}{\beta}+\frac{\beta}{\alpha}\) =
A) \(\frac{p^{2}-2 q}{q}\)
B) \(\frac{p^{2}+2 q}{q}\)
C) \(\frac{p^{2}-q}{q}\)
D) \(\frac{p^{2}+q}{q}\)
Answer:
D) \(\frac{p^{2}+q}{q}\)

Question 13.
If x = \(\sqrt{3+\sqrt{3+\sqrt{3+\ldots \ldots \infty} \infty}}\) then
A) x² – x + 3 = 0
B) x² + x + 3 = 0
C) x² – x – 3 = 0
D) x² + x – 3 = 0
Answer:
C) x²– x – 3 = 0

Question 14.
If the difference of two numbers is 5 and their product is 84, then the numbers
A) 14, 6
B) 12, 7
C) 21, 4
D) 14, 9
Answer:
B) 12, 7

Question 15.
\(\sqrt{6+\sqrt{6+\sqrt{6+\ldots \ldots \infty} \infty}}\) =
A) 1
B) 2
C) 3
D) 4
Answer:
C) 3

Question 16.
If x + \(\frac{1}{x}\) = 2, then x² + \(\frac{1}{x^{2}}\) =
A) 0
B) 2
C) 4
D) 8
Answer:
B) 2

Question 17.
The discriminant of the quadratic equation ax² + bx + c = 0is
A) b² – 4ac
B) a² – 4bc
C) c² – 4ab
D) None
Answer:
A) b² – 4ac

Question 18.
A ball is thrown vertically upward from the ground. The distance s in t seconds is given by s = 4t² + t – 3. After how many seconds does the ball come to rest?
A) 2s
B) 1s
C) \(\frac{3}{4}\)s
D) \(\frac{4}{3}\)s
Answer:
A) 2s

Question 19.
The product of the roots of √2x² – 10x + 5√2 = 0 is
A) 5√2
B) 5
C) 2√5
D) 2
Answer:
A) 5√2

Question 20.
The discriminant of \(\sqrt{x^{2}-5 x-1}\) = 2 is
A) 21
B) 23
C) 27
D) 45
Answer:
C) 27

Question 21.
The equation x² + x + 1 = 0 has
A) real equal roots
B) no real roots
C) real and unequal roots
D) All of the above a
Answer:
B) no real roots

Question 22.
If \(\frac{\mathbf{x}}{\mathbf{a}-\mathbf{b}}=\frac{\mathbf{a}}{\mathbf{x}-\mathbf{b}}\) then x = …………….
A) (b – a), -a
B) (b – a), \(\frac{1}{a}\)
C) (a – b), b²
D) (b – a), a
Answer:
D) (b – a), a

Question 23.
The discriminant of the equation x² + 4x + 2 = 0 is ……………….
A) 8
B) -8
C) 10
D) 4
Answer:
A) 8

Question 24.
The discriminant of the equation px² + qx + r = 0 is …………………..
A) q² + 4pr
B) q² – 4pr
C) p² – 4qr
D) r² – 4pq
Answer:
B) q² – 4pr

Question 25.
The degree of a quadratic equation is
A) 1
B) 0
C) 2
D) 3
Answer:
C) 2

Question 26.
In a quadratic equation ax² + bx + c = 0, if b² – 4ac > 0, then the roots are ……………….
A) real arid distinct
B) real and equal
C) imaginary
D) none
Answer:
A) real arid distinct

Question 27.
A quadratic equation, whose roots are 2 + √3 and 2 – √3 = ……………….
A) x² – x – 4 = 0
B) x² – 4x + 1 = 0
C) x² + 4x + 3 = 0
D) x² + x – 3 = 0
Answer:
B) x² – 4x + 1 = 0

Question 28.
The adjacent diagram indicates …………………

A) b² – 4ac >0
B) b² – 4ac = 0
C) b² – 4ac < 0
D) None of the given
Answer:
A) b² – 4ac >0

Question 29.
If \(\sqrt{x}+\frac{58}{\sqrt{x}}\) = 31, then x =
A) 529
B) 933
C) 729
D) 841
Answer:
D) 841

Question 30.
Which one of the following figures shows the quadratic equation
ax² + bx + c = 0 (a ≠ 0) having distinct roots ?

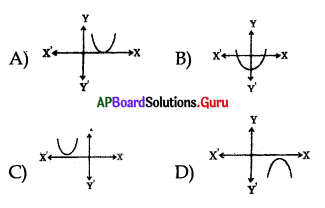
Answer:

Question 31.
If 1 is a common root of ax² + ax + 2 = 0 and x² + x + b = 0, then a. b = ………………
A) 2
B) -2
C) 3
D) -3
Answer:
A) 2

Question 32.
Find the zeros of the quadratic polynomial x² – 5x – 14.
A) (+7,-2)
B) (-7,-2)
C) (-7, +2)
D) (7, 2)
Answer:
A) (+7,-2)

Question 33.
If one root of the quadratic equation x² – 4x + 1 = 0 is 2 + √3, then the other
root is ……………………
A) 7 + √3
B) 7 – 4√3
C) 1 + √3
D) 2 – √3
Answer:
D) 2 – √3

Question 34.
If α, β are the roots of x² – 10x + 9 = 0, then | α – β|=
A) 9
B) 8
C) -10
D) 10
Answer:
B) 8

Question 35.
The number of diagonals in a polygon having ‘n’ sides is ………………..
A) \(\frac{n(n+1)}{2}\)
B) \(\frac{n(n-1)}{2}\)
C) \(\frac{n(n-3)}{2}\)
D) \(\frac{n(n+3)}{2}\)
Answer:
C) \(\frac{n(n-3)}{2}\)

Question 36.
If x²– px + q = 0(p,q ∈ Rand p ≠ 0,q ≠ 0) has distinct real roots, then………………
A) p² < 4q
B) p² > 4q
C) p² = 4q
D) p² + 4q = 0
Answer:
B) p² > 4q

Question 37.
If 5 is a root of x² – (K – 1)x + 10 = 0, then the value of K is
A) -8
B) 7
C) 8
D) 12
Answer:
C) 8

Question 38.
Sum of the roots of x² – 16 = 0 is
A) \(\frac{1}{16}\)
B) 1
C) 0
D) 16
Answer:
C) 0

Question 39.
The sum of squares of the roots of x² + 8x + 15 = 0 is …………………
A) 30
B) 34
C) 40
D) 44
Answer:
B) 34

Question 40.
The value of \(\sqrt{2+\sqrt{2+\sqrt{2+\ldots \ldots \ldots}}}\) is……………….
A) 3
B) 4
C) 2
D) 8
Answer:
C) 2

Question 41.
The roots of (b – c) x² + (c – a) x + (a – b) = 0 are equal and kb = a + c, then the value of k is………………..
A) 1
B) 2
C) 3
D) 4
Answer:
B) 2

Question 42.
The roots of x – \(\frac{3}{x}\) = 2 are
A) 1, 3
B) 3, -1
C) 2, 2
D) 1, 2
Answer:
B) 3, -1

Question 43.
If one root of 3x² + 2x + k = 0 is the reciprocal of the other, then the value of
k is
A) 3
B) -3
C) 2
D) 6
Answer:
A) 3

Question 44.
If the roots of 2x² + kx + 3 = 0 are real and equal, then the value of k is
A) ± 2√6
B) ± 6√2
C) ± 4
D) ± 5
Answer:
C) ± 4

Question 45.
The quadratic equation px² + qx + r = 0 has imaginary roots, if ………………
A) q² > 4 pr
B) q² < 4 pr
C) q² = 4 pr
D) p = q + r
Answer:
B) q² < 4 pr

Question 46.
Which of the following is a quadratic equation ?
A) x³ – 6x² + 2x -1 = 0
B) x² + \(\frac{1}{x^{2}}\) = 2
C) x + \(\frac{1}{x}\) = 3
D) (x + 1) (x + 2) (x + 3) = 0
Answer:
C) x + \(\frac{1}{x}\) = 3

Question 47.
The roots of the quadratic equation x² – 5x + 6 = 0 are ………………..
A) -2, 3
B) -2, -3
C) 2, -3
D) 2, 3
Answer:
D) 2, 3

Question 48.
The roots of the quadratic equation x² – 2x + 1 = 0 are
A) -1, -1
B) 1, -1
C) 1, 1
D) 2, 2
Answer:
C) 1, 1

Question 49.
The roots of the quadratic equation 3(x + 3)² = 48 are
A) 1, 7
B) 1, -7
C) -1, 7
D) -1, -7
Answer:
B) 1, -7

Question 50.
The roots of x² – 2x – (r² – 1) = 0 are
A) 1 – r, r + 1
B) 1, r
C) 1 – r, r
D) 1 – r, -r – 1
Answer:
A) 1 – r, r + 1

Question 51.
If 3 is a solution of 3x² + (k -1) x + 9 = 0, then k =
A) 13
B) 11
C) -11
D) -13
Answer:
C) -11

Question 52.
The roots of the quadratic equation \(\frac{x^{2}-8}{x^{2}+20}=\frac{1}{2}\) are ………………….
A) ± 2
B) ± 4
C) ± 3
D) ± 6
Answer:
D) ± 6

Question 53.
If x² + 2kx + 4 = 0 has a root x = 2, then ‘ the value of k is
A) 2
B) -2
C) -1
D) -4
Answer:
B) -2

Question 54.
The roots of the quadratic equation (3x – 2) (2x + 1) = 0 are
A) \(\frac{2}{3}, \frac{-1}{2}\)
B) \(\frac{-2}{3}, \frac{-1}{2}\)
C) \(\frac{-2}{3}, \frac{1}{2}\)
D) \(\frac{2}{3}, \frac{1}{2}\)
Answer:
A) \(\frac{2}{3}, \frac{-1}{2}\)

Question 55.
The roots of the quadratic equation (√3x – √2) (√3x – √2) = 0 are
A) \(\frac{\sqrt{2}}{\sqrt{3}}, \frac{\sqrt{2}}{\sqrt{3}}\)
B) \(\frac{-\sqrt{2}}{\sqrt{3}}, \frac{-\sqrt{2}}{\sqrt{3}}\)
C) \(\frac{\sqrt{2}}{\sqrt{3}}, \frac{-\sqrt{2}}{\sqrt{3}}\)
D) \(\frac{-\sqrt{2}}{\sqrt{3}}, \frac{\sqrt{2}}{\sqrt{3}}\)
Answer:
A) \(\frac{\sqrt{2}}{\sqrt{3}}, \frac{\sqrt{2}}{\sqrt{3}}\)

Question 56.
If \(\frac {1}{2}\) is a root of the equation x2 + kx – \(\frac {5}{4}\) = 0 then the value of k is
A) \(\frac {1}{2}\)
B) \(\frac {1}{4}\)
C) 2
D) -2
Answer:
C) 2

Question 57.
The roots of the quadratic equation \(\frac{x}{a}=\frac{a}{x}\) are
A) a, – a
B) -a², a²
C) -a, -a
D) a, a
Answer:
A) a, – a

Question 58.
The roots of the quadratic equation \(\frac{x^{2}}{a^{2}-b^{2}}=\frac{a+b}{a-b}\) are
A) ± a
B) a, b
C) ± (a + b)
D) ± b
Answer:
C) ± (a + b)

Question 59.
The roots of the quadratic equation \(\frac{11}{3+x}\) = 4(3 – x)are
A) ± 2
B) ± \(\frac{5}{2}\)
C)± \(\frac{1}{5}\)
D) ± 5
Answer:
A) ± 2

Question 60.
The roots of the quadratic equation \(\frac{9}{x^{2}-27}=\frac{25}{x^{2}-11}\) are
A) ± 6
C) ± 3
B) ± 4
D) ± 5
Answer:
A) ± 6

Question 61.
The roots of the quadratic equation x² + 7x = 0 are
A) 0, 7
B) 7, -7
C) -7, -7
D) 0, -7
Answer:
D) 0, -7

Question 62.
If (x + 4) (x – 4) = 9, then the values of x are
A) ± \(\frac {1}{2}\)
B) ± 5
C) \(\frac{1}{5}, \frac{1}{5}\)
D) 5, 5
Answer:
B) ± 5

Question 63.
The roots of the quadratic equation (2x + b + a) (2x + b – a) = 0 are
A) \(\frac{a-b}{2}, \frac{a-b}{2}\)
B) \(\frac{a+b}{2}, \frac{a+b}{2}\)
C) \(-\frac{a+b}{2}, \frac{a-b}{2}\)
D) \(\frac{a+b}{2}, \frac{a-b}{2}\)
Answer:
C) \(-\frac{a+b}{2}, \frac{a-b}{2}\)

Question 64.
The roots of the equation \(\sqrt{2 x^{2}+9}\) = 9 are
A) x = 0
B) x = ± 6
C) x = 6
D) x = -6
Answer:
B) x = ± 6

Question 65.
The value of k for which 3 is a root of the equation kx² – 7x + 3 = 0 is
A) -3
B) 3
C) 2
D) -2
Answer:
C) 2

Question 66.
The two roots of a quadratic equation are 2 and – 1. The equation is
A) x² + x + 2 = 0
B) x² – 2x + 2 = 0
C) x² + 2x – 2 = 0
D) x² – x – 2 = 0
Answer:
D) x² – x – 2 = 0

Question 67.
Which constant must be added and subtracted to solve the quadratic equation 9x² + 3x – 8 = 0 by the method of completing the square ?
A) \(\frac {1}{36}\)
B) \(\frac {9}{64}\)
C) \(\frac {1}{3}\)
D) \(\frac {1}{4}\)
Answer:
D) \(\frac {1}{4}\)

Question 68.
If the sum of the roots of the quadratic equation 3x² + (2k + 1) x – (k + 5) = 0 is equal to the product of the roots, then the value of k is
A) 3
B) 5
C) 4
D) 2
Answer:
C) 4

Question 69.
The quadratic equation whose one root is 3 + √5 is
A) x² – 6x – 4 = 0
B)x² + 6x + 4 = 0
C) x² – 6x + 4 = 0
D) x² + 6x + 5 = 0
Answer:
C) x² – 6x + 4 = 0

Question 70.
If the two roots of the two quadratic equations x² + mx + 1 = 0 and ax² + bx + a = 0 are common, then the value of m is
A) \(\frac{a}{b}\)
B) b
C) \(\frac{b}{a}\)
D) ab
Answer:
C) \(\frac{b}{a}\)

Question 71.
The roots of the quadratic equation x² + 8x + 7 = 0 are
A) 1, 7
B) -1, -7
C) -1, 7
D) 1, -7
Answer:
B) -1, -7

Question 72.
The value of k for which roots of the quadratic equation kx² + 2x + 3 = 0 are equal is …………………..
A) \(\frac{1}{3}\)
B) -3
C) \(\frac{-1}{3}\)
D) 3
Answer:
A) \(\frac{1}{3}\)

Question 73.
If the roots of the equation 12x² + mx + 5 = 0 are real and equal then m is equal to
A) 4\(\sqrt{15}\)
B) 2\(\sqrt{15}\)
C) 8\(\sqrt{15}\)
D) 10√5
Answer:
A) 4\(\sqrt{15}\)

Question 74.
If the roots of the quadratic equation x² + px + 16 = 0 are equal then the value of pis
A) ± 7
B) ± 6
C) ± 8
D) ± 9
Answer:
C) ± 8

Question 75.
Which of the following equations has the equal roots ?
A) 6x² – x – 2 = 0
B) x² – 8x + 16 = 0
C) 10x – \(\frac{1}{x}\) = 3
D) x² + 6x + 5 = 0
Answer:
B) x² – 8x + 16 = 0

Question 76.
Discriminant of the quadratic equation 2x² + x – 8 = 0 is
A) 65
B) -15
C) -127
D) 15
Answer:
A) 65

Question 77.
The discriminant of x² + 5x + 5 = 0 is
A) \(\frac{-5}{2}\)
B) \(\frac{5}{2}\)
C) – 5
D) 5
Answer:
D) 5

Question 78.
The value (s) of k such that the equation kx² + 6x + k = 0 has equal roots is ………………..
A) ± 3
B) ± 6
C)-6 and 3
D) 9
Answer:
A) ± 3

Question 79.
If the discriminant of the equation 6x² – bx + 2 = 0 is 1, then the value of ‘b’ is
A) ± 7
B)± √7
C) -7
D) 7
Answer:
A) ± 7

Question 80.
The discriminant of the quadratic equation 7√3x² + 10x – √3 = 0 is :
A) \(\frac{-10}{7 \sqrt{3}}\)
B) 142
C) 184
D) 26
Answer:
C) 184

Question 81.
Discriminant of the quadratic equation 2x² + x – 8 = 0 is
A) -65
B) 65
C) -127
D) -15
Answer:
B) 65

Question 82.
The roots of (x² – 3x + 2) (x) (x – 4) = 0 are
A) 0 and 4
B) 0, 1, 2 and 4
C) 4
D) 1, 2 and 4
Answer:
B) 0, 1, 2 and 4

Question 83.
The difference of the roots of x² – 7x – 9 = 0 is
A) \(\sqrt{85}\)
B) 7
C) -9
D) 8
Answer:
A) \(\sqrt{85}\)

Question 84.
The equation \(\sqrt{x+10}-\frac{6}{\sqrt{x+10}}\) = 5 has
A) an extraneous root between -5 and -1
B) two extraneous roots
C) an extraneous root between -10 and -6
D) a real root between 20 and 25
Answer:
C) an extraneous root between -10 and -6

Question 85.
If log₁₀(x² – 3x + 6) = 1, then the value of x is
A) 4 or -1
B) 4 only
C) 10 or 2
D) 4 or -2
Answer:
A) 4 or -1

Question 86.
If y = x + \(\) then x⁴ + x³ – 4x² + x + 1 = 0 becomes
A) x²(y² + y – 6) = 0
B) x²(y² + y – 3) = 0
C) x²(y² + y – 4) = 0
D) x²(y² + y – 2) = 0
Answer:
A) x²(y² + y – 6) = 0

Question 87.
The roots of the equations \(2 \sqrt{x}+2 x^{\frac{1}{2}}\) = 5 can be found by solving
A) 4x² – 25x -4 = 0
B) 4x² – 17x + 4 = 0
C) 4x² – 25x + 4 = 0
D) 4x² – 17x -4 = 0
Answer:
B) 4x² – 17x + 4 = 0

Question 88.
The values of ’k’ for which the equation 2x² – kx + x + 8 = 0 will have real and
equal roots are …………………
A) 9 and -7
B)-9 and 7
C) only 9
D) only -7
Answer:
A) 9 and -7

Question 89.
Two numbers whose sum is 6 and the absolute value of whose difference is 8 are the roots of the equation
A) x² – 6x + 8 = 0
B) x² – 6x – 7 = 0
C) x² – 6x + 7 = 0
D) x² + 6x – 8 = 0
Answer:
B) x² – 6x – 7 = 0

Question 90.
If a and b are the roots of x² – px + q = 0, then a² + b² =…………………
A) p² + 2q
B) p² – q²
C) p² – 2q
D) p² + q²
Answer:
C) p² – 2q

Question 91.
The solution of \(\sqrt{5 x-1}+\sqrt{x-1}\) = 2 is
A) x = 2
B) x = 2, x = 1
C) x = 1
D) x = 1, x = 4
Answer:
C) x = 1

Question 92.
The’ roots of \(\frac{15}{x^{2}-4}-\frac{2}{x-2}\) = = 1 are………………
A) -3 and 5
B) 3 only
C) -5 and 3
D) -5 only
Answer:
C) -5 and 3

Question 93.
In the equation 2x² – hx + 2k = 0, the sum of the roots is 4 and the product of the roots is -3. Then h and k have the values ………………… respectively.
A) 8 and -3
B) 8 and 6
C) 4 and -3
D) -3 and 8
Answer:
A) 8 and -3

Question 94.
If \(\sqrt{x-1}-\sqrt{x+1}\) + 1 = 0, then 4x equal to
A) 0
B) 1 \(\frac{1}{4}\)
C) 5
D) 4\(\sqrt{-1}\)
Answer:
C) 5

Question 95.
The number of roots satisfying the equation \(\sqrt{5-x}=x \sqrt{5-x}\) – x is/are
A) 2
B) 3
C) 1
D) unlimited
Answer:
B) 3

Question 96.
If α and β are the roots of the quadratic equation x² + px + 12 = 0 with the condition α – β = 1, then the value of ‘p’ is
A) 7 or -7
B) 1
C) -7
D) 7
Answer:
A) 7 or -7

Question 97.
The coefficient of x in the quadratic equation x² + px + q = 0 was taken as 17 in the place of 13 and its roots were found to be-2 and-15. The roots of the original equation are
A) 3 or -10
B) -3 or 10
C) -3 or -10
D) 3 or 10
Answer:
C) -3 or -10

Question 98.
The roots of \(\sqrt{2 x-3}+\sqrt{3 x-5}-\sqrt{5 x-6}\) = 0 are
A) 2 or \(\frac{7}{6}\)
B) 2 only
C) \(\frac{7}{6}\) only
D) 2 and \(\frac{7}{6}\)
Answer:
A) 2 or \(\frac{7}{6}\)

Question 99.
If one of roots of x² + ax + 4 = 0 is twice the other root, then the value of ‘a’ is
A) 8√2
B) √2
C) -3√2
D) -2√2
Answer:
C) -3√2

Question 100.
If the roots of the equation
(a – b)x² + (b – c) x + (c – a) = 0 are equal, then
A) 2b = a + c
B) 2c = a + b
C) 2a = b + c
D) 2a = b – c
Answer:
C) 2a = b + c

Question 101.
If a = b = c, then the roots of the equa-tion (x – a) (x – b) + (x – b)(x – c) +
(x – c) (x – a) = 0 are
A) imaginary
B) real and equal
C) real and unequal
D) real
Answer:
B) real and equal

Question 102.
If the sum of the roots of the quadratic equation 3x² + (2k + 1) x – (k + 5) = 0 is equal to the product of the roots, then the value of ‘k’ is
A) 0
B) 1
C) -4
D) 4
Answer:
D) 4

Question 103.
For a quadratic equation, 3 + √5 is one root. The other root must be
A) 3 + √5
B) 3 – √5
C) 3 + 2√5
D) 3 – 2√5
Answer:
B) 3 – √5

Question 104.
If one root of the equation ax² + bx + c = 0 is three times the other, then …………………
A) b² = 16ac
B) 3b² = 16ac
C) 2b² = 9ac
D) b² = ac
Answer:
B) 3b² = 16ac

Question 105.
The root of the quadratic equation 3x² – kx + 14 = 0 are in the ratio 7 : 6 then k = ………………….
A) 12
B) -3
C) 1
D) 13
Answer:
D) 13

Question 106.
If α, β are the roots of the equation x² – px + q = 0, then the quadratic equation whose roots are \(\frac{\alpha}{\beta}\) and \(\frac{\boldsymbol{\beta}}{\alpha}\) is ……………………
A) qx² + (2q – p²) x + q = 0
B) qx² – px + 1 = 0
C) qx² + (p² – 2q) x + q = 0
D) qx² – px – 1 = 0
Answer:
A) qx² + (2q – p²) x + q = 0

Question 107.
Find the value of k, if the expression x² + kx + 1 is factorizable into two linear factors ………………
A) either k ≥ 2 or k ≤ -2
B) k ≥ 2
C) k ≤ -2
D) neither k ≥ 2 nor k ≤ – 2
Answer:
A) either k ≥ 2 or k ≤ -2

Question 108.
The product of two consecutive odd numbers is 143. The numbers are
A) 13 and 15
B) 11 and 13
C) -11 and 13
D) -13 and 15
Answer:
B) 11 and 13

Question 109.
The perimeter of a rectangular room is 34m and the length of a diagonal is 13m. The dimensions of the room are …………………..
A) 17m and 7m
B) 12m and 5m
C) 9m and 2m
D) 15m and 2m
Answer:
B) 12m and 5m

Question 110.
If x² + 4ax + 3 = 0 and 2x² + 3ax – 9 = 0 have a common root, then the value of ‘a’is ……………………
A) 1
B) ± 3
C) ± 1
D) -3
Answer:
C) ± 1

Question 111.
The product of two consecutive natural numbers is 600. The numbers are …………………….
A) 35, 36
B) 16, 25
C) 26, 25
D) 24, 25
Answer:
D) 24, 25

Question 112.
The roots of the quadratic equation x² – 5x + 6 = 0 are
A) 3, -2
B) -3, 2
C) 2, 3
D) -2, -3
Answer:
C) 2, 3

Question 113.
If the roots of a quadratic equation are equal, then
A) b² = 4ac
B) b² – 4ac < 0
C) b² – 4ac > 0
D) b² – 4ac = 0
Answer:
A) b² = 4ac

Question 114.
The roots of the quadratic equation abx² – (a + b) x + 1 are
A) a + b, a – b
B) \(\frac{1}{a}, \frac{1}{b}\)
C) a, b
D) \(\frac{1}{a+b}, \frac{1}{a-b}\)
Answer:
B) \(\frac{1}{a}, \frac{1}{b}\)

Question 115.
If α, β be the roots of the quadratic equation x² – 2x + 1 = 0, then the quadratic equation whose roots are α + β and αβ is ………………
A) x² – 2x – 1 = 0
B) x² + 2x + 1 = 0
C) x² + 2x -1 = 0
D) x² – 2x + 1 = 0
Answer:
D) x² – 2x + 1 = 0

Question 116.
The roots of the equation x + \(\) = 5\(\) are
A) 5, -5
B) 5, \(\frac{1}{5}\)
C) -5, -5
D) 5, 5
Answer:
B) 5, \(\frac{1}{5}\)

Question 117.
Which of the following is not a quadratic equation ?
A) x (2x + 3) = x² + 1
B) (x – 2)² + 1 = 2x – 3
C) x(x + 1) + 8 = (x + 2) (x – 2)
D) (x + 2)³ = x³ – 4
Answer:
C) x(x + 1) + 8 = (x + 2) (x – 2)

Question 118.
Is – √5x² + 6x + 3 = 0 a quadratic equation ?
A) Yes
B) No
C) can’t say
D) It is a linear equation
Answer:
A) Yes

Question 119.
Which of the following equation has \(\frac {1}{5}\) as a root ?
A) 2x² – 7x + 6 = 0
B) 35x² – 2x – 1 = 0
C) 35x² + 12x + 1 = 0
D) 10x² – 3x – 1 = 0
Answer:
B) 35x² – 2x – 1 = 0

Question 120.
If x = 1 is a common root of the equations ax² + ax + 3 = 0 and x² + x + b = 0, then the value of ab is :
A) 3
B) 6
C) 3.5
D) -3
Answer:
A) 3

Question 121.
Which of the following equations has the sum of roots as 3 ?
A) 2x² – 3x + 6 = 0
B) 3x² – 3x + 3 = 0
C) √2 x²–\(\frac{3}{\sqrt{2}}\)x + = 0
D) -x² + 3x – 3 = 0
Answer:
D) -x² + 3x – 3 = 0

Question 122.
Which constant should be added and substracted to solve the quadratic equation 4x² – √3x – 5 = 0 by the method of completing the square?
A) \(\frac{3}{16}\)
B) \(\frac{\sqrt{3}}{4}\)
C) \(\frac{9}{16}\)
D) \(\frac{3}{4}\)
Answer:
A) \(\frac{3}{16}\)

Question 123.
Which of the following equations has the product of its roots as 4 ?
A) x² + 4x – 4 = 0
B) x² + 4x + 4 = 0
C) x² + 4x – 24 = 0
D) -x² + 4x + 4 = 0
Answer:
B) x² + 4x + 4 = 0

Question 124.
ax² + bx + c = 0, a > 0,b = 0, c > 0 has;
A) Two equal roots
B) One real root
C) Two distinct real roots
D) No real roots
Answer:
D) No real roots

Question 125.
If the equation x² – 4x + a = 0 has no real roots, then
A) a ≤ 4
B) a < 2
C) a < 4 D) a > 4
Answer:
D) a > 4

Question 126.
If the discriminant of the quadratic equation ax² + bx + c = 0, then the roots of the equation
A) are irrational and equal
B) are rational and equal
C) do not exist and real
D) are real and equal
Answer:
D) are real and equal

Question 127.
The least value of ax² + bx + c (a > 0) is
A) \(\frac{-b}{2 a}\)
B) \(\frac{4 a^{2}-b^{2}}{4 a}\)
C) \(\frac{4 a^{2}+b^{2}}{4 a}\)
D) none of the above
Answer:
B) \(\frac{4 a^{2}-b^{2}}{4 a}\)

Question 128.
The equation x + \(\sqrt{x-2}\) = 4 has
A) two real roots
B) two imaginary roots
C) one real root
D) one real and one imaginary root
Answer:
C) one real root

Question 129.
If one root of the equation a(b – c) x² + b(c – a) x + c(a – b) = 0 is 1, then the other root is
A) \(\frac{a(b-c)}{c(a-b)}\)
B) \(\frac{a(b-c)}{b(c-a)}\)
C) \(\frac{c(a-b)}{a(b-c)}\)
D) \(\frac{b(c-a)}{a(b-c)}\)
Answer:
C) \(\frac{c(a-b)}{a(b-c)}\)

Question 130.
The roots of the equation x² + 2√3 x + 3 = 0 are
A) rational and equal
B) real and equal
C) rational and unequal
D) imaginary
Answer:
B) real and equal

Question 131.
The roots of the equation ax² + bx + c = 0 will be reciprocal if
A) a = bc
B) b = c
C) a = b
D) c = a
Answer:
D) c = a

Question 132.
The discriminant of ax² – 2√2 x + c = 0 with a, c and real constants is zero. The roots must be
A) rational and equal
B) real and equal
C) imaginary
D) equal and integral
Answer:
B) real and equal

Question 133.
The equation \(\sqrt{x+4}-\sqrt{x-3}\) + 1 = 0 has
A) one real root
B) two imaginary roots
C) no root
D) one real and one imaginary root
Answer:
C) no root

Question 134.
The sum of the reciprocals of the roots of the equation x² + px + q = 0 is
A) \(\frac{q}{p}\)
B) \(\frac{-\mathrm{p}}{\mathrm{q}}\)
C) \(\frac{-\mathrm{q}}{\mathrm{p}}\)
D) \(\frac{\mathrm{p}}{\mathrm{q}}\)
Answer:
D) \(\frac{\mathrm{p}}{\mathrm{q}}\)

Question 135.
The equation \(x-\frac{7}{x-3}=3-\frac{7}{x-3}\) has
A) no roots
B) infinitely many roots
C) one integral root
D) two real roots
Answer:
A) no roots

Question 136.
If \(\frac{b}{x-a}=\frac{x+a}{b}\) then the value of x in terms of a and b is
A) \(\sqrt{a^{2}+b^{2}}\)
B) \(\pm \sqrt{a^{2}+b^{2}}\)
C) \(-\sqrt{a^{2}+b^{2}}\)
D) \(\pm \sqrt{a^{2}-b^{2}}\)
Answer:
B) \(\pm \sqrt{a^{2}+b^{2}}\)

Question 137.
The standard form of a quadratic equation is
A) ax + b = 0, a ≠ 0
B) ax² + bx + c = 0, a ≠ 0
C) ax³ + bx² + cx + d = 0, a ≠ 0
D) ax⁴ + bx³ + cx² + dx + e = 0, a ≠ 0.
Answer:
B) ax² + bx + c = 0, a ≠ 0

Question 138.
Which of the following is a quadratic equation?
A) (x – 2) (x + 1) = (x – 1) (x + 3)
B) x⁴ – 1 = 0
C) (x + 1)² = 2(x – 3)
D) x² + 3x + 1 = (x – 2)²
Answer:
C) (x + 1)² = 2(x – 3)

Question 139.
A cottage industry produces a certain number of toys in a day. The cost of production of each toy was found to be 55 rupees. On a particular day, the total cost of production was ? 750. Represent this situation in the form of a quadratic equation.
A) x (55 – x) = 750
B) 55x = 750
C) x(x – 55) = 750
D) x (x + 55) = 750
Answer:
A) x (55 – x) = 750

Question 140.
The sum of the squares of two consecutive natural numbers is 25. Represent this situation in the form of a quadratic equation.
A) x² + (x + 1)² + 25 = 0
B) x² – (x + 1)² = 25
C) x² + (x + 1)² = 25
D) (x + 1)² – x² = 25
Answer:
C) x² + (x + 1)² = 25

Question 141.
If one root of the two quadratic equations x² + ax + b = 0 and x² + bx + a = 0 is common, then
A) a + b = -1
B) ab = -1
C) ab = 1
D) a + b = 1
Answer:
A) a + b = -1

Question 142.
The condition that both the roots of the two quadratic equations
a₁x2 + b₁x + c₁ = 0 and a₂x2 + b₂x + c₂ = 0 are common is
A) a₁a₂ + b₁b₂ + c₁c₂ = 0
B) a₁² + b₁² + c₁² = a₂² + b₂² + c₂²
C) \(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}\)
D) a₁ + b₁ + c₁ = a₂ + b₂ + c₂
Answer:
C) \(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}\)

Question 143.
If x = \(\sqrt{1+\sqrt{1+\sqrt{1+\ldots \ldots \ldots . .}}}\) , then
A) 1 < x < 2
B) x = 1
C) 0 < x < 1
D) x is infinite
Answer:
A) 1 < x < 2

Question 144.
If \(\) has roots which are numerically equal but of opposite signs, the value of ‘m’ must be
A) \(\frac{a+b}{a-b}\)
B) 0
C) 1
D) \(\frac{a-b}{a+b}\)
Answer:
D) \(\frac{a-b}{a+b}\)

Question 145.
Two consecutive positive integers differ by
A) 3
B) 4
C) 2
D) 1
Answer:
D) 1

Question 146.
The sum of a number and its reciprocal is \(\frac {5}{2}\) . Represent this, situation in the form of a quadratic equation.
A) x –\(\frac{1}{x}=\frac{5}{2}\)
B) x +\(\frac{1}{x}=\frac{5}{2}\)
C) x +\(\sqrt{x}=\frac{5}{2}\)
D) x²\(\frac{1}{x^{2}}=\frac{5}{2}\)
Answer:
B) x +\(\frac{1}{x}=\frac{5}{2}\)

Question 147.
Two consecutive even integers are
A) x, x + 1
B) x, 2x
C) x, x – 1
D) x, x + 2
Answer:
D) x, x + 2

Question 148.
Two consecutive positive integers are
A) x, x – 2
B) x, x + 1
C) x, x + 2
D) x, 2x
Answer:
B) x, x + 1

Question 149.
John and Jivanti together have 45 marbles. Both of them lost 5 marbles each and the product of the number of marbles they have now is 124. Represent this situation in the form of quadratic equation.
A) (x – 5) (x – 40) = 124
B) (x + 5) (40 + x) + 124 = 0
C) (x – 5) (40 – x) = 124
D) (5 + x) (40 – x) = 124
Answer:
C) (x – 5) (40 – x) = 124

Question 150.
What is the condition that one root of the quadratic equation ax² + bx + c is reciprocal of the other ?
A) a = b
B) b = c
C) a = c
D) a + b + c = 0
Answer:
C) a = c

Question 151.
If the roots of the quadratic equation ax² + bx + c are sinα and cosα, then
A) a² + b² = c²
B) b² – 2ac = a²
C) b² + 2ac = a²
D) a²2 – 2bc = b²
Answer:
B) b² – 2ac = a²

Question 152.
If the difference of the roots of the quadratic equation x² – ax + b is 1, then
A) a² – 4b = -1
B) a² – 4b = 4
C) a² – 4b = 1
D) a² – 4b = 0
Answer:
C) a² – 4b = 1

Question 153.
The value of c for which the equation ax² + bx + c = 0 has equal roots is
A) \(\frac{\mathrm{b}^{2}}{4 \mathrm{a}}\)
B) \(\frac{a^{2}}{b}\)
C) \(\frac{a^{2}}{4 b}\)
D) \(\frac{\mathrm{b}^{2}}{\mathrm{a}}\)
Answer:
A) \(\frac{\mathrm{b}^{2}}{4 \mathrm{a}}\)

Question 154.
The roots of the equation x² – 2x = 0 can be obtained graphically by finding the abscissa of the points of intersection of each of the following pairs of equations except ………………….
A) y = x,y = x – 2
B) y = x² – 2x + 1, y = 1
C) y = x²,y = 2x
D) y = x² – 2x, y = 0
Answer:
A) y = x,y = x – 2

Question 155.
If in applying the quadratic f ormula to a quadratic equation f(x) = ax² + bx + c = 0 it happens that c = \(\). Then the graph of y = f(x) will certainly …………….
A) have a minimum
B) be a tangent to the Y – axis
C) have a maximum
D) be a tangent to X-axis
Answer:
D) be a tangent to X-axis

Question 156.
In the equation \(\) the roots are equal when
A) m = 0
B) m = \(\frac {1}{2}\)
C) m = –\(\frac {1}{2}\)
D) m = 1
Answer:
C) m = –\(\frac {1}{2}\)

Question 157.
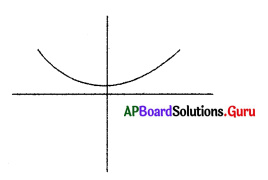
If b² – 4ac > 0 the graph may be …………………

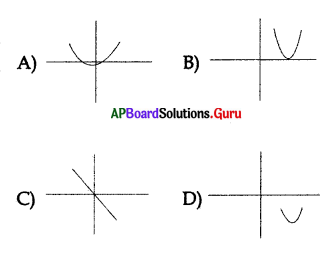
Answer:

Question 158.
If b² = 4ac then the graph may be

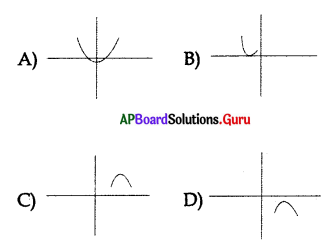
Answer:

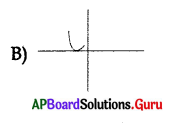
Question 159.
The graph of a linear polynomial may be

Answer:

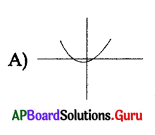
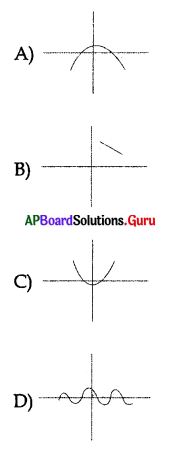
Question 160.
Identify parabola among the following graphs.

Answer:

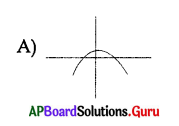
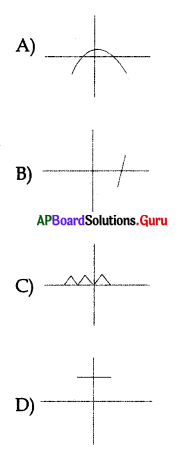
Question 161.
If a quadratic equation have no real roots then the graph may be ………………

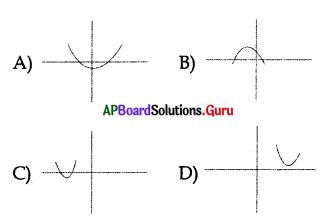
Answer:

Question 162.
If the graph of ax² + bx + c = 0, a ≠ 0 never intersects X axis then the number of real zeroes are ………………..
A) 2
B) 0
C) 3
D) 4
Answer:
B) 0

Question 163.
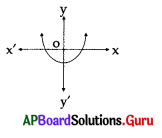
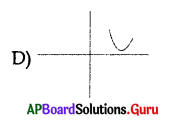
From the graph given below the nature of roots are ………………….

A) Real and equal
B) Real and not equal
C) Not real
D) 10, 11
Answer:
C) Not real