AP 10th Class Maths Bits Chapter 3 Polynomials with Answers

Practice the AP 10th Class Maths Bits with Answers Chapter 3 Polynomials on a regular basis so that you can attempt exams with utmost confidence.

AP State Syllabus 10th Class Maths Bits 3rd Lesson Polynomials with Answers

Question 1.
Zero of the polynomial (3x – 1) is ………………
A) 3
B) 0
C) \(\frac{1}{3}\)
D) 1
Answer:
C) \(\frac{1}{3}\)

Question 2.
The zeroes of the polynomial (shown in the graph) are

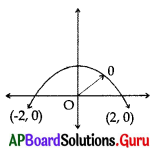
A) 2, 0
B) 0,-2
C) -2, 2
D) 0, 0
Answer:
C) -2, 2

Question 3.
The remainder of 3x³ – 2x² + x + 2 when divided by 3x + 1 is
A) \(\frac{4}{3}\)
B) \(\frac{3}{4}\)
C) –\(\frac{4}{3}\)
D) None
Answer:
A) \(\frac{4}{3}\)

Question 4.
If α, β, are the roots of 5x² + 5x + 6 = 0, then (1 + α) (1 + β) =
A) ) –\(\frac{4}{3}\)
B) ) \(\frac{3}{5}\)
C) ) \(\frac{6}{5}\)
D) ) –\(\frac{6}{5}\)
Answer:
C) ) \(\frac{6}{5}\)

Question 5.
If two zeroes of the polynomial x³ – 5x² + 6x are 2 and 3, then the third zero is
A) 0
B) 5
C) 6
D) 1
Answer:
A) 0

Question 6.
If ‘4’ is one of the zeroes of p(x) = x² + kx – 8, then the value of k = ………………
A) 1
B) -1
C) 2
D) -2
Answer:
D) -2

Question 7.
If the roots of x² + 6x + 5 = 0 are α and β, then α + β = ………………..
A) 5
B) -6
C) 6
D) -1
Answer:
B) -6

Question 8.
If α, β are the zeroes of x² + x + 1, then \(\frac{1}{\alpha}+\frac{1}{\beta}\) = ……………………
A) 1
B) -1
C) 2
D) -2
Answer:
B) -1

Question 9.
The degree of the polynomial
√2 X²– 3X + 1 = …………………..
A) √2
B) 3
C) 1
D) 2
Answer:
D) 2

Question 10.
If one zero of the polynomial f (x) = 5x² + 13x + k is reciprocal of the , other, then the value of k = …………………..
A) 13
B) 5
C) -5
D) – \(\frac{13}{5}\)
Answer:
B) 5

Question 11.
A quadratic polynomial, the sum of whose zeroes is zero and one zero is 4, is ………………..
A) x² – 16
B) x² + 16
C) x² – 4
D) x² + 4
Answer:
A) x² – 16

Question 12.
Sum of zeroes of a polynomial x³ – 2x² + 3x – 4 is ……………….
A) -2
B) 2
C) 1
D) 4
Answer:
B) 2

Question 13.
The number of zeroes of the polynomial whose graph is given below:

A) 0
B) 1
C) 2
D) 3
Answer:
D) 3

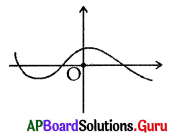
Question 14.
The graph represented by y = x is …………………

Answer:

Question 15.
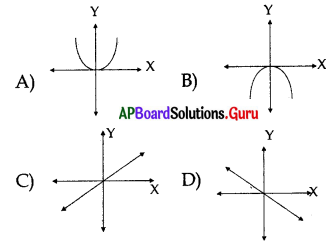
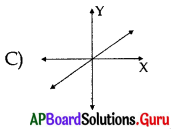
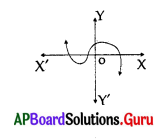Number of zeroes can be identified by the adjacent figure.
A) 0
B) 1
C) 2
D) 3
Answer:
D) 3

Question 16.
If α and β are the zeroes of the polynomial p(x) = 3x² – x – 4, then αβ = ………………..
A) \(\frac{1}{3}\)
B) –\(\frac{1}{3}\)
C) \(\frac{4}{3}\)
D) –\(\frac{4}{3}\)
Answer:
D) –\(\frac{4}{3}\)

Question 17.
If p(x) = 5x⁷ – 6x⁵ + 7x – 6, then the degree of p (x) is …………….
A) 0
B) 1
C) 5
D) 7
Answer:
D) 7

Question 18.
A factor of x³ – 3x² + x + 1 is
A) x + 1
B) 2x – 1
C) 2x + 1
D) x – 1
Answer:
D) x – 1

Question 19.
The length of a rectangular dining hall is twice of its breadth. If x represents the breadth of the hall and its area is 5 sq. units, then the polynomial equation which represents the situation is
A) 5x² – 2 = 0
B) 2x² – 5 = 0
C) x² – 25 = 0
D) None
Answer:
B) 2x² – 5 = 0

Question 20.
The sum of the zeros of the polynomial p(x) = x² + 7x + 10 is
A) 7
B) -7
C) 10
D) -10
Answer:
B) -7

Question 21.
If p(x) = 2x² + 3x – 5, then p(2) =
A) 2
B) 9
C) 0
D) -5
Answer:
B) 9

Question 22.
If p (x) = 3x – k and p (1) = 0 then k =
A) 3
B) -3
C) -1
D) +1
Answer:
A) 3

Question 23.
The value of (x – √3)(x + √3) = ………………..
A) x² + 3
B) x² – 3
C) x + 9
D) x – 9
Answer:
B) x² – 3

Question 24.
If α and β are the two zeroes of a polynomial x² – 5x + 6 then the value of \(\frac{1}{a^{2}}+\frac{1}{\beta^{2}}\) is ……………….
A) \(\frac{13}{36}\)
B) \(\frac{17}{36}\)
C) \(\frac{19}{36}\)
D) \(\frac{23}{36}\)
Answer:
A) \(\frac{13}{36}\)

Question 25.
If α, β are the two zeroes of the polynomial f(x) = x² – p (x +1) – c, then (α + 1)(β + 1) = …………………
A) c – 1
B) 1 – c
C) c
D) 1 + c
Answer:
B) 1 – c

Question 26.
If α and β are the roots of ax² + bx + c = 0, then α³ + β³ =
A) \(\frac{3 a b c-b^{3}}{a^{3}}\)
B) \(\frac{3 a b c-b^{3}}{c^{3}}\)
C) \(\frac{b^{2}-3 a b c}{a^{3}}\)
D) \(\frac{b^{2}-3 a b c}{c^{3}}\)
Answer:
A) \(\frac{3 a b c-b^{3}}{a^{3}}\)

Question 27.
The equation whose roots are obtained by adding 1 to those of 2x² + 3x + 5 = 0 is
A) 2x² – x – 4 = 0
B) 2x² + x – 4 = 0
C) 2x²2 – x + 4 = 0
D) None
Answer:
C) 2x²2 – x + 4 = 0

Question 28.
If x + 1, x + 2 are two factors of x³ + 3x² -2αx + β, then values of α + β is ……………………
A) – 1
B) 1
C) -2
D) 2
Answer:
A) – 1

Question 29.
If α, β are zeroes of the polynomial
ax² + bx + c, then the value of \(\frac{1}{\alpha}+\frac{1}{\beta}\) is…………………
A) \(\frac{-b}{a c}\)
B) b = ac
C) \(\frac{-b}{c}\)
D) \(-\sqrt{\frac{b}{a c}}\)
Answer:
C) \(\frac{-b}{c}\)

Question 30.
The value of ‘K’ for which 2x⁴ + 3x³ + 2Kx² + 3x + 6 is exactly divisible by x + 2?
A) 1
B) -1
C) 2
D) -2
Answer:
B) -1

Question 31.
The degree of the polynomial 5x⁷ – 6x⁵ + 7x – 6 is
A) 4
B) 5
C) 6
D) 7
Answer:
D) 7

Question 32.
The zero of the linear polynomial px + q is ………………..
A) \(-\frac{q}{p}\)
B) \(\frac{\mathrm{p}}{\mathrm{q}}\)
C) \(-\frac{p}{q}\)
D) q
Answer:
A) \(-\frac{q}{p}\)

Question 33.
The quadratic polynomial, whose zeroes are 2 and 3, is
A) x² – 5x – 6
B) x² + 5x – 6
C) x² – 5x + 6
D) x² + 5x + 6
Answer:
C) x² – 5x + 6

Question 34.
Which of the following is a polynomial with only one zero ?
A) p(x) = 2x² – 3x + 4
B) p(x) = x² – 2x + 1
C) p(x) = 2x + 3
D) p(x) = 5
Answer:
C) p(x) = 2x + 3

Question 35.
Observe the given rectangular figure, then its area in polynomial function is …………………..

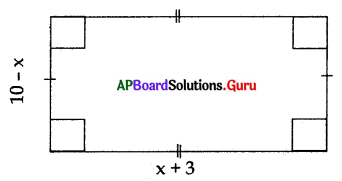
A) A(x) = x² + 7x + 30
B) A(x) = – x² + 7x + 30
C) A(x) = x² – 7x + 30
D) A (x) = -x² – 7x + 30
Answer:
B) A(x) = – x² + 7x + 30

Question 36.
For the expression f(x) = x³ + ax² + bx + c if f(1) = f(2) = 0 and f(4) = f(0). Find the values of a, b, c.
A) a = -8, b = -20, c = 12
B) a = 9, b = -20, c = -12
C) a = -9, b = 20, c = -12
D) a = -8, b =. 20, c = -12
Answer:
C) a = -9, b = 20, c = -12

Question 37.
If (x⁴ + ax³ – 7x² – 8x + b) is completely divisible by (x² + 5x + 6). Then the values of a and b are ……………………..
A) a = 2, b = 8
B) a = -2, b = 6
C) a = 2, b = 12
D) a = 2, b = 14
Answer:
C) a = 2, b = 12

Question 38.
x³ + 2X² + ax + b is exactly divisible by (x² – 1). The values of a and b is ………………
A) a = -1, b = 2
B) a = 1, b = -2
C) a = 1, b = 2
D) a = -1, b = -2
Answer:
D) a = -1, b = -2

Question 39.
Find the remainder when x⁴ + 15x³ + 6x² – 12x + 3 is divided by x + 2 ? ………………….
A) -53
B) 53
C) -52
D) 52
Answer:
A) -53

Question 40.
If x² + x -1 is a factor of x⁴ + px³ + qx² – 1 then the values of p and q can be …………………
A) 2, 1
B) -2, -1
C) -1,-2
D) 1, -2
Answer:
A) 2, 1

Question 41.
If the zeroes of the rational expression (ax + b) (3x + 2) are \(\frac{-2}{3}\) and \(\frac{1}{2}\) then a + b = …………………..
A) -1
B) 0
C) -b
D) 1
Answer:
C) -b

Question 42.
Simplify \(\frac{x+1}{x-1}+\frac{x-1}{x+1}-\frac{2 x^{2}-2}{x^{2}+1}\)
A) \(\frac{4 x^{4}+2}{x^{4}-1}\)
B) \(\frac{8 x^{2}}{x^{4}-1}\)
C) \(\frac{4 x^{2}}{x^{4}-1}\)
D) 1
Answer:
B) \(\frac{8 x^{2}}{x^{4}-1}\)

Question 43.
Find f(4),f(-5),f (3.2) if f (x) = 6.2x² – 4x³ + 4.28 ………………
A) f(4) = -152.53, f(-5) = 659.28, f(3.2) = 63.304
B) f(4) = -152.52, f(-5) = -659.28, f(3.2) = 63.304
C) f(4) = -152.52, f(-5) = 659.28, f(3.2) = -63.304
D) f(4) = -152.52, f(-5) = 659.27, f(3.2) = -63.304
Answer:
C) f(4) = -152.52, f(-5) = 659.28, f(3.2) = -63.304

Question 44.
The product of x³ + 2x² – 3x + 4 and 2x² – 5x + 1 is …………………
A) 2x⁵ – x⁴ – 15x³ + 25x² – 23x + 4
B) 2x⁵ – x⁴ – 15x³ + 25x² – 23x – 4
C) 2x⁵ – x⁴ – 15x³ – 25x² – 23x – 4
D) 2x⁵ – x⁴ – 15x³ – 23x – 4
Answer:
A) 2x⁵ – x⁴ – 15x³ + 25x² – 23x + 4

Question 45.
If A = \(\frac{x-1}{x+1}\) then 2A – \(\frac{1}{2 A}\) = ……………….
A) \(\frac{3 x^{2}-10 x-3}{2\left(x^{2}-1\right)}\)
B) \(\frac{3 x^{2}-10 x+3}{2\left(x^{2}-1\right)}\)
C) \(\frac{3 x^{2}+10 x+3}{2\left(x^{2}-1\right)}\)
D) \(\frac{3 x^{2}-10 x+1}{x^{2}-1}\)
Answer:
B) \(\frac{3 x^{2}-10 x+3}{2\left(x^{2}-1\right)}\)

Question 46.
If P = \(\frac{x+1}{x-1}\) and Q = \(\frac{x-1}{x+1}\) then P² + Q² – 2PQ = …………………..
A) \(\frac{4 x^{4}+8 x^{2}+4}{x^{4}-2 x+1}\)
B) \(\frac{4 x^{2}}{x^{4}+2 x^{2}+1}\)
C) \(\frac{16 x^{2}}{x^{4}-2 x^{2}+1}\)
D) \(\frac{8 x^{2}}{x^{4}-2 x^{2}+1}\)
Answer:
C) \(\frac{16 x^{2}}{x^{4}-2 x^{2}+1}\)

Question 47.
The rational expression A = \(\left(\frac{x+1}{x-1}-\frac{x-1}{x+1}-\frac{4 x}{x^{2}+1}\right)\) is multiplied with the additive inverse of B = \(\frac{1-x^{4}}{4 x}\) to get C, then C = ……………..
A) 2
B) \(\frac{2 x}{x^{4}-1}\)
C) \(\frac{32 x^{2}}{x^{4}-1}\)
D) 1
Answer:
A) 2

Question 48.
The product of additive inverse of \(\frac{x^{2}-1}{2 x}\) and \(\frac{x^{2}-4}{3-x}\) is …………………….
A) x² + x – 6
B) x² – x – 6
C) x² – 5x + 6
D) x² + 5x + 6
Answer:
A) x² + x – 6

Question 49.
If (x – 1) and (x + 3) are the factors of x³ + 3x² – x – 3 then the other factor is …………………
A) x + 1
B) x – 3
C) x + 2
D) x – 1
Answer:
A) x + 1

Question 50.
A rational expression whose numerator is a quadratic polynomial with zeroes, 1 and 2 and whose denominator is monomial with zero 3 is ………………….
A) \(\frac{x^{2}+x-2}{x+3}\)
B) \(\frac{x^{2}-x-2}{x+3}\)
C) \(\frac{x^{2}+x-2}{x-3}\)
D) \(\frac{x^{2}-x-2}{x-3}\)
Answer:
D) \(\frac{x^{2}-x-2}{x-3}\)

Question 51.
Simplify \(\frac{\left(a^{2}-b^{2}\right)^{3}+\left(b^{2}-c^{2}\right)^{3}+\left(c^{2}-a^{2}\right)^{3}}{(a-b)^{3}+(b-c)^{3}+(c-a)^{3}}\)
A) 1
B) 3(a + b) (b + c) (c + a)
C) (a + b) (b + c) (c + a)
D) 2(a + b) (b + c) (c + a)
Answer:
C) (a + b) (b + c) (c + a)

Question 52.
Find “a” and “b” in order that x³ – 6x² + ax + b may be exactly divisible by x² – 3x + 2.
A) a = 11, b = -5
B) a = 11, b = 6
C) a = 11, b = -6
D) a = -11, b = -5
Answer:
B) a = 11, b = 6

Question 53.
If g(x) = x⁶ + 3x⁴ – 24x² + 3 find g(1), g(2) and g(3).
A) g(1) = -12, g(2) = 19, g(3) = 759
B) g(1) = 12, g(2) = 19, g(3) = 758
C) g(1) = -12, g(2) = -19, g(3) = -759
D) g(1) = -12, g(2) = -19, g(3) = 759
Answer:
A) g(1) = -12, g(2) = 19, g(3) = 759

Question 54.
If the zeroes of the rational expression (3x + 2a) (2x + 1) are \(\frac{-1}{2}\) and \(\frac{\mathbf{b}}{3}\) then the value of a is ……………………..
A) \(\frac{-b}{3}\)
B) \(\frac{-b}{2}\)
C) \(\frac{-2 b}{3}\)
D) \(\frac{2 b}{3}\)
Answer:
B) \(\frac{-b}{2}\)

Question 55.
If ‘a’ and ‘b’ are unequal and x² + ax + b and x² + bx + a have a common factor, then a + b = ……………………
A) -1
B) 1
C) 0
D) 2
Answer:
A) -1

Question 56.
Find the quadratic polynomial in x, which when divided by (x – 1) (x – 2) and (x – 3) leaves remainders of 11, 22 and 37 …………………….
A) 2x² + 5x + 4
B) 2x² – 5x – 3
C) 3x² – 5x + 4
D) 2x² – 5x + 4
Answer:
A) 2x² + 5x + 4

Question 57.
The sum of \(\left(\frac{x-1}{x+1}\right)\) and its reciprocal is ……………………
A) \(\frac{x^{2}+1}{x^{2}-1}\)
B) \(\frac{2\left(x^{2}+1\right)}{x^{2}-1}\)
C) \(\frac{x^{2}-1}{x^{2}+1}\)
D) \(\frac{2\left(x^{2}-1\right)}{x^{2}+1}\)
Answer:
B) \(\frac{2\left(x^{2}+1\right)}{x^{2}-1}\)

Question 58.
The value of 6a + 11b if x³ – 6x² + ax + b is exactly divisible by (x² – 3x + 2) is ………………………
A) 0
B) 66
C) 132
D) 1
Answer:
A) 0

Question 59.
If 4x⁴ -(a – 1) x³ + ax² – 6x – 1 is divisible by 2x – 1, the value of a …………………..
A) 28
B) 29
C) 27
D) 26
Answer:
B) 29

Question 60.
If f(x) = x² + 5x + p and g(x) = x² + 3x + q have a common factor then (p – q)² = ………………….
A) 2(3p – 5q)
B) 5p – 3q
C) 3p – 5q
D) 2(5p – 3q)
Answer:
A) 2(3p – 5q)

Question 61.
If (x – 4) is the HCF of p(x) = x² – nx -12 and q(x) =x² – mx – 8 then the simplest form of \(\frac{p(x)}{q(x)}\) is …………………
A) \(\frac{x+2}{x+3}\)
B) \(\frac{x+3}{x-2}\)
C) \(\frac{x+3}{x+2}\)
D) \(\frac{x-2}{x-3}\)
Answer:
B) \(\frac{x+3}{x-2}\)

Question 62.
Simplify \(\frac{x^{2}-(y-2 z)^{2}}{x-y+2 z}\) + \(\frac{y^{2}-(2 x-z)^{2}}{y+2 x-z}\) + \(\frac{z^{2}-(x-2 y)^{2}}{z-x+2 y}\) is ……………………
A) 1
B) x + y + z
C) 0
D) x – y – z
Answer:
C) 0

Question 63.
If P= \(\frac{1+2 x}{1-2 x}\) and Q = \(\frac{1-2 x}{1+2 x}\) then \(\frac{P-Q}{P+Q}\) = ………………..
A) \(-\frac{4 x}{1+4 x^{2}}\)
B) \(\frac{1+4 x^{2}}{4 x}\)
C) \(\frac{-(1+4 x)^{2}}{4 x}\)
D) \(\frac{4 x}{1+4 x^{2}}\)
Answer:
A) \(-\frac{4 x}{1+4 x^{2}}\)

Question 64.
If α, β,γ are the zeroes of 3x³ – 5x² – 11x – 3 then α + β + γ = ……………….
A) \(\frac{-5}{3}\)
B) \(\frac{5}{3}\)
C) \(\frac{-11}{3}\)
D) 1
Answer:
B) \(\frac{5}{3}\)

Question 65.
If x⁴ – 2x³ + 3x² – mx + 5 is exactly divisible by (x – 3) then m = …………………
A) \(\frac{-40}{3}\)
B) \(\frac{6}{40}\)
C) -40
D) 40
Answer:
D) 40

Question 66.
Find the values of “a” and “b” so that (x + 2) and (x – 1) may be factors of x³ + 10x² + ax + b.
A) a = 7,b = -18
B) a = 7, b = -17
C) a = 7, b = -15
D) a = 7, b = 17
Answer:
A) a = 7,b = -18

Question 67.
Simplify \(\frac{(x+y)^{2}-z^{2}}{(x+y+z)^{2}}\) ÷ \(\left\{\frac{(x-z)^{2}-y^{2}}{x^{2}+x y+z x} \div \frac{(x-y)^{2}-z^{2}}{x^{2}-x y-z x}\right\}\) …………………….
A) \(\frac{1}{x+y+z}\)
B) 1
C) x + y + z
D) 2
Answer:
B) 1

Question 68.
The expression 2x³ + ax² + bx – 2 leaves a remainder 7 and 0 when divided by (2x – 3) and (x + 2). Find the values of a and b.
A) a = 3, b = -3
B) a = -3, b = -3
C) a = -3, b = 3
D) a = 3, b = 3
Answer:
A) a = 3, b = -3

Question 69.
Find the value of k if the expressions
p(x) = kx³ + 4x² + 3x – 4 and
q(x) = x³ – 4x + k leave the same remainder when divided by (x – 3)
A) k = -1
B) k = 4
C) k = 3
D) k = -2
Answer:
A) k = -1

Question 70.
If a + c + e = 0 and b + d = 0 then ax⁴ + bx³ + cx² + dx + e is exactly divisible by ……………………….
A) x + 1
B) x – 1
C) (x + 1) and (x – 1)
D) (x + 2) and (x – 2)
Answer:
C) (x + 1) and (x – 1)

Question 71.
Simplify \(\frac{1}{1+x+x^{2}}\) – \(\frac{1}{1-x+x^{2}}\) + \(\frac{2 x}{1+x^{2}+x^{4}}\) ………………
A) \(\frac{1}{1+x^{2}+x^{4}}\)
B) 0
C) \(\frac{-1}{1+x^{2}+x^{4}}\)
D) \(\frac{2 x-3}{1+x^{2}+x^{4}}\)
Answer:
B) 0

Question 72.
What should be subtracted from x³ – 2x² + 4x + 1 to get 1 ? ( )
A) x³ – 2x² + 4x + 1
B) x³ + 2x² + 4x + 1
C) x³ – 2x² + 4x
D) x³ – 2x² + 4x -1
Answer:
C) x³ – 2x² + 4x

Question 73.
What should be subtracted from \(\frac{7 x}{x^{2}-x-12}\) to get \(\frac{3}{x+3}\) ?
A) \(\frac{1}{x-4}\)
B) \(\frac{2}{x-4}\)
C) \(\frac{4}{x-4}\)
D) \(\frac{5}{x+4}\)
Answer:
C) \(\frac{4}{x-4}\)

Question 74.
If ax² + 2a²x + b³ is divisible by (x + a) then …………………..
A) a² + ab + b² = 0
B) a = b
C) either a = b or a² + ab + b² = 0
D) neither a = b nor a² + ab + b² = 0
Answer:
C) either a = b or a² + ab + b² = 0

Question 75.
Which of the following expressions is a rational expression ?
A) \(\frac{5 x^{2}-\sqrt{6} x+7}{x+3}\)
B) \(\frac{\sqrt{2} x^{2}-4 \sqrt{x}+5}{x-\sqrt{2}}\)
C) x³ – √3x² + √5x – 11
D) \(\frac{x^{2}+3}{2 \sqrt{x}-1}\)
Answer:
C) x³ – √3x² + √5x – 11

Question 76.
Express x – \(\frac{1}{x}\) as a rational expression,
A) \(\frac{x^{2}-1}{x}\)
B) \(\frac{1-x^{2}}{x}\)
C) \(\frac{1-x}{x}\)
D) \(\frac{x-1}{x}\)
Answer:
A) \(\frac{x^{2}-1}{x}\)

Question 77.
Which of the following expressions is a polynomial ?
A) 3x² -2√5x + 7
B) \(\frac{x^{3}-2 x+1}{2 x+5}\)
C) \(\frac{x^{2}-5 x+6}{x-3}\)
D) \(\frac{x^{2}-2 x+1}{2 x+7}\)
Answer:
C) \(\frac{x^{2}-5 x+6}{x-3}\)

Question 78.
How much is a² + 2ab + b² more than a² – 2ab + b² ?
A) -4ab
B) 4ab
C) 6ab
D) -3ab
Answer:
B) 4ab

Question 79.
Which of the following is true ?
A) The sum of two rational expressions is always a rational expression
B) \(\frac{p(x)}{q(x)}\) is in its lowest terms if LCM [p(x), q(x)] = 1.
C) The difference of two rational expressions is always a rational expression.
D) Reciprocal of \(\frac{-2 x}{x^{2}-1}\) is \(\frac{x^{2}-1}{2 x}\)
Answer:
A) The sum of two rational expressions is always a rational expression

Question 80.
Simplify \(\frac{a^{2}-(b-c)^{2}}{(a+c)^{2}-b^{2}}+\frac{b^{2}-(a-c)^{2}}{(a+b)^{2}-c^{2}}\) + \(\frac{c^{2}-(a-b)^{2}}{(b+c)^{2}-a^{2}}\)
A) a + b + c
B) \(\frac{1}{a+b+c}\)
C) 1
D) 0
Answer:
C) 1

Question 81.
What should be subtracted from \(\left(\frac{2 x^{2}+2 x-7}{x^{2}+x-6}\right)\) to get \(\left(\frac{x-1}{x+2}\right)\)
A) \(\frac{x-2}{x-3}\)
B) \(\frac{x+2}{x+3}\)
C) \(\frac{x+2}{x-3}\)
D) \(\frac{x-2}{x+3}\)
Answer:
B) \(\frac{x+2}{x+3}\)

Question 82.
The rational expression \(\) in lowest term is ……………………..
A) \(\frac{x-2}{y}\)
B) \(\frac{x+1}{y}\)
C) \(\frac{x+1}{x y}\)
D) \(\frac{x-2}{y}\)
Answer:
D) \(\frac{x-2}{y}\)

Question 83.
The expression \(\frac{1}{1-x}-\frac{1}{1+x}-\frac{x^{3}}{1-x}+\frac{x^{2}}{1+x}\) in lowest term is ……………………..
A) x² + 2x
B) x² – 2x
C) x² + 2
D) 2x + 1
Answer:
A) x² + 2x

Question 84.
Simplify \(\frac{81 x^{4}-16 x^{2}+32 x-16}{9 x^{2}-4 x+4}\)
A) 9x² – 2x – 8
B) 9x² + 2x – 8
C) 9x² – 4x – 4
D) 9x² + 4x – 4
Answer:
D) 9x² + 4x – 4

Question 85.
What should be added to \(\frac{1}{x^{2}-7 x+12}\) to get \(\frac{2}{x^{2}-6 x+8}\)
A)\(\frac{1}{x^{2}-5 x+6}\)
B) \(\frac{-1}{x^{2}+5 x-6}\)
C) \(\frac{4}{(x+3)(x+2)}\)
D) \(\frac{2}{(x+3)(x-2)}\)
Answer:
A)\(\frac{1}{x^{2}-5 x+6}\)

Question 86.
Express \(\frac{2 x^{3}-54}{x^{3}+3 x^{2}+9 x}\) in lowest terms
A) \(\frac{2 x-6}{x}\)
B) \(\frac{2(x-4)}{x^{2}}\)
C) \(\frac{2(4-x)}{x}\)
D) \(\frac{6-2 x}{x}\)
Answer:
A) \(\frac{2 x-6}{x}\)

Question 87.
What should be added to \(\frac{4 x}{x^{2}-1}\) to get \(\frac{x+1}{x-1}\) ?
A) \(\frac{x-1}{x^{2}-1}\)
B) \(\frac{x-1}{x+1}\)
C) \(\frac{x^{2}-1}{x+1}\)
D) \(\frac{x^{2}+1}{x+1}\)
Answer:
B) \(\frac{x-1}{x+1}\)

Question 88.
xⁿ – y is divisible by (x – y) when n is ………………….
A) a prime number
B) an odd number
C) an even number
D) a natural number
Answer:
D) a natural number

Question 89.
Express \(\frac{\left(x^{3}+y^{3}+z^{3}-3 x y z\right)}{\left(x^{2}+y^{2}+z^{2}-x y-y z-z x\right)}\) in lowest terms.
A) x + y + z
B) x + y- z
C) x – y + z
D) x – y – z
Answer:
A) x + y + z

Question 90.
Which of the following algebraic expressions are not polynomials ?
1) x³ + 2x³ + √7x + 4
2) 5x² + √4x – 11
3) \(\frac{x^{3}+3 x^{2}-8 x+11}{4 x \sqrt{x}-3 x+3}\)
4) \(\frac{x^{3}+3 x^{2}-6 x+13}{x^{2}+1}\)
A) 1, 2 and 3
B) 1 and 3
C) 2 and 3
D) 1 and 4
Answer:
C) 2 and 3

Question 91.
Simplify \(\frac{x+2}{x-2}+\frac{x-2}{x+2}-\frac{3 x^{2}-3}{x^{2}+4}\)
A)\(-\frac{x^{4}-21 x^{2}+20}{x^{4}-16}\)
B) \(\frac{x^{4}+31 x^{2}+20}{x^{4}-16}\)
C) \(\frac{x^{4}+31 x^{2}+20}{x^{4}-16}\)
D) \(\frac{-x^{4}+31 x^{2}+20}{x^{4}-16}\)
Answer:
D) \(\frac{-x^{4}+31 x^{2}+20}{x^{4}-16}\)

Question 92.
What should be added to \(\frac{2}{x^{2}+x-6}\) get \(\frac{-4 x}{\left(x^{2}-4\right)\left(x^{2}-9\right)}\)
A) \(\frac{-2}{x^{2}-x-6}\)
B) \(\frac{4 x}{x^{2}+x+6}\)
C) \(\frac{-3}{x^{2}+x+6}\)
D) \(\frac{4}{x^{2}-x-6}\)
Answer:
A) \(\frac{-2}{x^{2}-x-6}\)

Question 93.
Simplify \(\frac{3 x+2}{x^{2}-16}+\frac{x-5}{(x+y)^{2}}\)
A)\(\frac{4 x^{2}+5 x+28}{x^{3}+4 x^{2}+16 x-64}\)
B) \(\frac{4 x^{2}+5 x+28}{x^{3}-4 x^{2}-16 x-64}\)
C) \(\frac{4 x^{2}+5 x-28}{x^{3}-4 x^{2}-16 x-64}\)
D) \(\frac{4 x^{2}+5 x+28}{x^{3}+4 x^{2}-16 x-64}\)
Answer:
D) \(\frac{4 x^{2}+5 x+28}{x^{3}+4 x^{2}-16 x-64}\)

Question 94.
The additive inverse of 3x – 4 + \(\frac{x}{2 x-1}\) is …………………
A) -3x + 4 + \(\frac{x}{2 x-1}\)
B) -3x + 4 – \(\frac{x}{1-2 x}\)
C) -3x + 4 – \(\frac{x}{2 x-1}\)
D) -3x + 4 – \(\frac{x}{2 x+1}\)
Answer:
C) -3x + 4 – \(\frac{x}{2 x-1}\)

Question 95.
Which of the following is not a quadratic polynomial?
A) (x – 2) (x + 2) – (x² + 5x)
B) 1 – (x² – 2x)
C) x² – 5x – 6
D) x² + 5x + 6
Answer:
A) (x – 2) (x + 2) – (x² + 5x)

Question 96.
Which of the following polynomials is in standard form ?
A) 24x³ – 14x² – 39x + 20
B) 20 – 39x – 14x² + 24x³
C) 24x³ – 39x – 14x² + 20
D) 24x³ – 39x – 14x² + 28x³
Answer:
A) 24x³ – 14x² – 39x + 20

Question 97.
Which of the following is not a zero of the polynomial x³ – 6x² + 11x – 6?
A) 1
B) 2
C) 3
D) 0
Answer:
D) 0

Question 98.
The graph of y = ax² + bx + c is called
A) line
B) axis
C) polynomial
D) parabola
Answer:
D) parabola

Question 99.
Which of the following is not a polynomial?
A) \(x^{\frac{3}{4}}\) – 7x + 4
B) x⁴ – 3x + 2
C) 2 – 3y + 6y² – 2y³
D) 5x² – 6x + 3
Answer:
A) \(x^{\frac{3}{4}}\) – 7x + 4

Question 100.
For the polynomials p(x) and q(x)
A) LCM and HCF are not equal
B) Cannot be determined
C) LCM and HCF are equal
D) Can be determined
Answer:
C) LCM and HCF are equal

Question 101.
xⁿ + yⁿ is divisible by (x + y) when ‘n’ is ……………….
A) a natural number
B) a prime number
C) an odd number
D) an even number
Answer:
C) an odd number

Question 102.
A linear polynomial from the following is ………………………
A) ax + b
B) bx² + c
C) ax³ + bx² + cx + e
D) ax² + bx + c
Answer:
A) ax + b

Question 103.
No. of zeroes of (x – 3)² is ………………..
A) 4
B) 2
C) 3
D) 1
Answer:
D) 1

Question 104.
The polynomial 2x – 1 cuts X axis at ……………….
A) (-2, 0)
B) (0, 1)
C (\(\frac {1}{2}\) , 0)
D)(-3, 0)
Answer:
C (\(\frac {1}{2}\) , 0)

Question 105.
Number of zeroes of x² – 7x + 12 is ……………….
A) 4
B) 7
C) 2
D) 1
Answer:
C) 2

Question 106.
The product of two consecutive numbers is 56. Find ……………….
A) -8, -7
B) 8, -7
C) -8, 7
D) 8, 7
Answer:
A) -8, -7

Question 107.
If we divide 36x² – 12x + 1- 49y² by 6x + 7y -1, then the quotient is ………………
A) 6x + 1 + 7y
B) 6x – 1 – 7y
C) 6x + 2 + 7y
D) -6x -1 – 7y
Answer:
B) 6x – 1 – 7y

Question 108.
The zeroes of ax² + bx + c; a ≠ 0 is ………………
A) x = \(\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}\)
B) x = \(\frac{b-\sqrt{b^{2}-a c}}{2}\)
C) x = \(\frac{-a-\sqrt{b^{2}-4}}{a}\)
D) x = \(\frac{-b-\sqrt{a^{2}-b}}{2}\)
Answer:
A) x = \(\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}\)

Question 109.
If the polynomial has only one zero its cuts X axis at ……………………. point.
A) 4
B) 2
C) 3
D) 1
Answer:
D) 1

Question 110.
Maximum number toots of a cubic polynomial is …………………
A) 2
B) 4
C) 3
D) 5
Answer:
C) 3

Question 111.
\(\frac{1}{x^{2}+1}\) is a …………………..
A) Polynomial
B) Binomial
C) Multinomial
D) 0
Answer:
C) Multinomial

Question 112.
For the graph of y = p(x) given below where p(x) is the polynomial, the number of zeroes of p(x) is ………………..

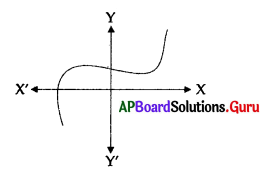
A) 0
B) 3
C) 2
D) 1
Answer:
D) 1

Question 113.
Which of the following graph represents a straight line ?

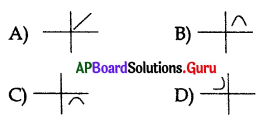
Answer:

Question 114.
How many zeroes are there for the polynomial from the given graph ?

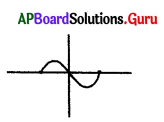
A) 4
B) 3
C) 1
D) 2
Answer:
B) 3

Question 115.
The graph of y = x² may be ………………….

Answer:

Question 116.
If the polynomial has no real zeroes then the graph can be represented as ………………

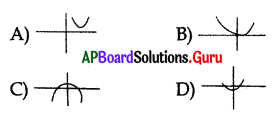
Answer:

Question 117.
-x² = y can be represented as …………………..

Answer:

Question 118.
Which of the following is a parabola

Answer:

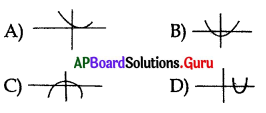
Question 119.
If the quadratic polynomial has only one zero the graph may be ……………..

Answer: