AP 10th Class Maths Bits Chapter 1 Real Numbers with Answers

Practice the AP 10th Class Maths Bits with Answers Chapter 1 Real Numbers on a regular basis so that you can attempt exams with utmost confidence.

AP State Syllabus 10th Class Maths Bits 1st Lesson Real Numbers with Answers

Question 1.
In the rational form of a terminating decimal number prime factor of the denominator is ………………..
A) only 2
B) only 5
C) 2 or 5 only
D) any prime
Answer:
C) 2 or 5 only

Question 2.
log₁₀2 + log₁₀5 value = ……………….
A) 1
B) 2
C) 5
D) 10
Answer:
A) 1

Question 3.
If P₁ and P₂ are two odd prime numbers such that P₁ > P₂, then P₁² -P₂² is ……………..
A) an even number
B) an odd number
C) a prime number
D) an odd prime number
Answer:
A) an even number

Question 4.
The HCF of two consecutive natural numbers is
A) 1
B) 2
C) 3
D) 4
Answer:
A) 1

Question 5.
The fundamental theorem of arithmetic is applicable to
A) 4
B) 3
C) 2
D) 1
Answer:
A) 4

Question 6.
The last digit of 6⁵⁰ is ………………..
A) 1
B) 6
C) 2
D) 3
Answer:
B) 6

Question 7.
A rational number that equals to 2.\(\overline{6}\) is
A) \(\frac{7}{3}\)
B) \(\frac{8}{3}\)
C) \(\frac{16}{7}\)
D) \(\frac{17}{7}\)
Answer:
B) \(\frac{8}{3}\)

Question 8.
The value of log₂₅ 5 = …………………
A) \(\frac{1}{2}\)
B) 2
C) 5
D) 25
Answer:
A) \(\frac{1}{2}\)

Question 9.
The value of log_√2 64 is ………………..
A) -6
B) 12
C) 6
D) 8
Answer:
B) 12

Question 10.
Which is the three digit number divisible by 7 ?
A) 100
B) 133
C) 137
D) 143
Answer:
B) 133

Question 11.
Which one of the following rational numbers have non-terminating repeating decimal expansion ?
A) \(\frac{31}{3125}\)
B) \(\frac{71}{512}\)
C) \(\frac{23}{200}\)
D) None of these
Answer:
D) None of these

Question 12.
Logarithmic form of \(\sqrt[3]{8}\) = 2 is
A) log₈ 2 = \(\frac{1}{3}\)
B) log₂ 8 = \(\frac{1}{3}\)
C) \(\log _{\frac{1}{3}}\) 8 = 2
D) \(\log _{\frac{1}{3}}\) 2 = 0
Answer:
A) log₈ 2 = \(\frac{1}{3}\)

Question 13.
The relation a . (b . c) = (a . b). c is
A) distributive law
B) associative law
C) commutative law
D) closure law
Answer:
A) distributive law

Question 14.
The HCF of 1.2 and 0.12 is
A) 1.2
B) 12
C) 0.12
D) 120
Answer:
C) 0.12

Question 15.
The value of log₃ 243 =
A) 5
B) 6
C) 4
D) 8
Answer:
A) 5

Question 16.
0.10110111011110 …………….. is
A) an integer
B) a rational number
C) an irrational number
D) a natural number
Answer:
C) an irrational number

Question 17.
The LCM of the numbers 2⁷ × 3⁴ × 7 and 2³ × 3⁴ × 11 is
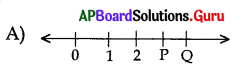
A) 2³ × 3⁴
B) 2⁷ × 3⁴
C) 2⁷ × 3⁴ × 7 × 11
D) 2³ × 3⁴ × 7 × 11
Answer:
C) 2⁷ × 3⁴ × 7 × 11

Question 18.
The number of rational numbers exist between any two distinct rational numbers is
A) 0
B) 1
C) 2
D) infinite
Answer:
D) infinite

Question 19.
The prime factorization of 163800 is
A) 2² × 3³ × 5⁵ × 7 × 13
B) 2³ × 3² × 5² × 7 × 13
C) 2³ × 3² × 5⁵ × 7 × 13
D) None
Answer:
B) 2³ × 3² × 5² × 7 × 13

Question 20.
\(\frac{1}{\log _{x} x y}+\frac{1}{\log _{y} x y}\)
A) 0
B) 1
C) -1
D) 2
Answer:
B) 1

Question 21.
If log₁₀3 = 0.4771, then the value of log 15 + log 2 =
A) 47.71
B) 1.4771
C) 4.77
D) 0.4771
Answer:
B) 1.4771

Question 22.
The value of \(\sqrt{\frac{x}{y}+2+\frac{y}{x}}\) =
A) \(\frac{x}{\sqrt{y}}+\frac{\sqrt{y}}{x}\)
B) \(\frac{x}{y}+\frac{y}{x}\)
C) \(\sqrt{\frac{x}{y}}+\sqrt{\frac{y}{x}}\)
D) \(\frac{\sqrt{x}}{y}+\frac{y}{\sqrt{x}}\)
Answer:
C) \(\sqrt{\frac{x}{y}}+\sqrt{\frac{y}{x}}\)

Question 23.
√3 + √5 is a …………………
A) positive rational number
B) negative rational number
C) positive irrational number
D) negative irrational number
Answer:
C) positive irrational number

Question 24.
If a + b = 5, ab = 6, then a³ + b³ =
A) 5
B) 25
C) 35
D) 125
Answer:
C) 35

Question 25.
2 log 3 – 3 log 2 =
A) log 0
B) log 1
C) log (\(\frac{9}{8}\))
D) log (72)
Answer:
C) log (\(\frac{9}{8}\))

Question 26.
log₂ . log₂₅ 5 =
A) 0
B) 1
C) -1
D) \(\frac{1}{2}\)
Answer:
C) -1

Question 27.
If a^x = \(\left(\frac{a}{k}\right)^{y}\) = k^m then \(\frac{1}{x}-\frac{1}{y}\) =
A) 0
B) 1
C) m
D) \(\frac{1}{\mathrm{~m}}\)
Answer:
D) \(\frac{1}{\mathrm{~m}}\)

Question 28.
The H.C.F. of the numbers 3⁷ × 5³ × 2⁴ and 3² × 7⁴ × 2⁸is …………………
A) 2⁴ × 3²
B) 2⁸ × 3⁷ × 5³ × 7⁴
C) 2⁸ × 3⁷
D) 2 × 3 × 5 × 7
Answer:
A) 2⁴ × 3²

Question 29.
The expanded form of log \(\frac{343}{125}\) is …………………
A) 7 (log 5 – log 7)
B) 4 (log 5 – log7)
C) 2 (log 7 – log 5)
D) 3 (log 7 – log 5)
Answer:
D) 3 (log 7 – log 5)

Question 30.
The value of \(\log _{10}^{0.01}\) is ……………….
A) -1
B) -2
C) -10
D) 0.01
Answer:
B) -2

Question 31.
log \(\left[\frac{x+y}{3}\right]\) = \(\frac{1}{2}\) (log x + log y), then the value of \(\frac{x}{y}+\frac{y}{x}\) is ………………….
A) 9
B) 5
C) 7
D) 11
Answer:
C) 7

Question 32.
log₁₀2 = 0.3010 the number of digits in 4²⁰¹⁷is …………….
A) 2015
B) 2016
C) 1215
D) 1214
Answer:
C) 1215

Question 33.
If a = b² = c³ then log_c ab = ………………..
A) \(\frac{9}{2}\)
B) \(\frac{2}{9}\)
C) \(\frac{4}{9}\)
D) \(\frac{1}{3}\)
Answer:
A) \(\frac{9}{2}\)

Question 34.
If x = log₂ 3 and y = log₂ 5, then log₂15 in terms of x and y is
A) x – y
B) x + y
C) xy
D) x + y – 1
Answer:
B) x + y

Question 35.
If a² + b² = c² then log_a(c – b)
+ log_a(c + b) = ………………..
A) -1
B) -2
C) 1
D) 2
Answer:
B) -2

Question 36.
Identify the terminating decimal.
A) \(\frac{2}{3}\)
B) \(\frac{8}{9}\)
C) \(\frac{3}{8}\)
D) \(\frac{1}{7}\)
Answer:
C) \(\frac{3}{8}\)

Question 37.
Number of two digit numbers divisible by 3 is ……………….
A) 10
B) 20
C) 40
D) 30
Answer:
D) 30

Question 38.
log₁₀125 + log₁₀8 =
A) 1
B) 2
C) 3
D) None
Answer:
C) 3

Question 39.
The relation a (b + c) = ab + ac is
A) commutative law
B) associative law
C) distributive law
D) None
Answer:
C) distributive law

Question 40.
If n is a natural number, then 8ⁿ – 3ⁿ is always divisible by ……………..
A) 3
B) 5
C) 8
D) 11
Answer:
B) 5

Question 41.
√P + √Q is ………………….
A) real number
B) irrational number
C) natural number
D) rational number
Answer:
A) real number

Question 42.
\(\sqrt{\frac{a}{b}+\frac{b}{a}-2}\) = …………………
A) \(\sqrt{\frac{a}{b}}-\sqrt{\frac{b}{a}}\)
B) \(\sqrt{\frac{a}{b}}+\sqrt{\frac{b}{a}}\)
C) \(\frac{\mathrm{a}}{\sqrt{\mathrm{b}}}+\frac{\mathrm{b}}{\sqrt{\mathrm{a}}}\)
D) \(\frac{a}{b}+\frac{b}{a}\)
Answer:
A) \(\sqrt{\frac{a}{b}}-\sqrt{\frac{b}{a}}\)

Question 43.
G.C.F. of 12,18 is
A) 36
B) 6
C) 12
D) 18
Answer:
B) 6

Question 44.
The rational number betwen the pair of numbers \(\frac{1}{2}\) and √1 is
Answer:
A) \(\frac{9}{4}\)
B) \(\frac{3}{4}\)
C) \(\frac{5}{4}\)
D) \(\frac{7}{4}\)
Answer:
B) \(\frac{3}{4}\)

Question 45.
The prime factorisation of 729 is
A) 3⁶
B) 3⁵
C) 3⁴
D) 3⁸
Answer:
A) 3⁶

Question 46.
The number of prime factors of 36 is ……………………..
A) 4
B) 3
C) 2
D) 1
Answer:
C) 2

Question 47.
The exponential form of log₁₀0.001 = -3 is …………………..
A) (0.001)¹⁰ = -3
B) (-3)¹⁰ = 0.001
C) (10)³ =-0.001
D) (10)^-3 = 0.001
Answer:
D) (10)^-3 = 0.001

Question 48.
Which of the following is true for an irrational number ?
i) Which can be written in the form of \(\frac{p}{q}\) where p, q ∈ Z, q ≠ 0.
ii) Which cannot be written in the form of \(\frac{p}{q}\) , where p, q ∈ Z, q ≠ 0.
iii) Non – terminating repeating decimals.
iv) Non – terminating, non – repeating decimals.
A) (i), (iii)
B) (ii), (iv)
C) (i) only
D) (iii) only
Answer:
B) (ii), (iv)

Question 49.
The HCF of the polynomials
(x² – 4x + 4) (x + 3) and (x² + 2x – 3) (x – 2) is …………………
A) x + 3
B) x – 2
C) (x + 3) (x – 2)
D) (x + 3) (x – 2)²
Answer:
C) (x + 3) (x – 2)

Question 50.
\(\sqrt{3+\sqrt{5}}\) = ……………….
A) √2 + 12.
B) \(\sqrt{\frac{8}{2}}+\sqrt{\frac{1}{2}}\)
C) \(\sqrt{\frac{7}{2}}-\sqrt{\frac{1}{2}}\)
D) \(\sqrt{\frac{9}{2}}-\sqrt{\frac{3}{2}}\)
Answer:
C) \(\sqrt{\frac{7}{2}}-\sqrt{\frac{1}{2}}\)

Question 51.
The sum of LCM and HCF of two numbers is 1260. If their LCM is 900 more than their HCF, find the product of two numbers.
A) 205400
B) 194400
C) 109440
D) 29590
Answer:
B) 194400

Question 52.
Find the remainder when the square of any prime number greater than 3 is divided by 6.
A) 6
B) 7
C) 9
D) 1
Answer:
D) 1

Question 53.
If HCF (72, q) = 12 then how many values can q take ?
A) 2
B) 1
C) 4
D) 8
Answer:
A) 2

Question 54.
Find the HCF of 120 and 156.
A) 42
B) 12
C) 19
D) 48
Answer:
B) 12

Question 55.
Find the HCF of 432 and 504.
A) 86
B) 72
C) 96
D) 108
Answer:
B) 72

Question 56.
The LCM of two numbers is 1200. Which of the following cannot be their HCF ?
A) 600
B) 500
C) 800
D) 700
Answer:
A) 600

Question 57.
How many prime factors are there in the prime factorization of 240 ?
A) 3
B) 20
C) 25
D) 6
Answer:
A) 3

Question 58.
The largest number among √2, 3√3 and 4√4 is ………………..
A) √2
B) 3√3
C) 4√4
D) all are equal
Answer:
C) 4√4

Question 59.
The expression (x + y)^-1 (x^-1 + y^-1) is the reciprocal of …………………..
A) x + y
B) xy
C) \(\frac{1}{\mathrm{xy}}\)
D) \(\frac{x}{y}\)
Answer:
C) \(\frac{1}{\mathrm{xy}}\)

Question 60.
The greatest possible length of a scale that can be used to measure exactly 3cm,
5cm, 10cm and 90cm is ……………….
A) 40 cm
B) 80 cm
C) 90 cm
D) 60 cm
Answer:
D) 60 cm

Question 61.
If (x -1)² + (y – 2)⁴ + (z – 3)⁶ = 0 then the
value of xyz is ………………..
A) 1
B) 6
C) 14
D) 0
Answer:
B) 6

Question 62.
a^x = b^y = c^z and abc = 1 then \(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}\) = ………………….
A) 0
B) abc
C) a + b + c
D) \(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\)
Answer:
A) 0

Question 63.
If 0.\(\overline{7}\) = \(\frac{\mathbf{p}}{\mathbf{q}}\) then p + q = ……………………..
A) 16
B) 15
C) 12
D) 14
Answer:
A) 16

Question 64.
For what values of x, 2^x × 5^x ends with 8 or 5 ? ( )
A) 10
B) 8
C) 5
D) None
Answer:
D) None

Question 65.
If 7^{x + 3} = 5^{x + 3} then the value of ‘x’ is ……………………
A) -3
B) 3
C) 2
D) -2
Answer:
A) -3

Question 66.
= …………………
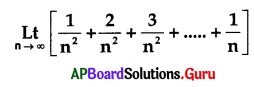A) 0
B) 1
C) 1
D) \(\frac{1}{2}\)
Answer:
A) 0

Question 67.
If a + b + c = 1 and \(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\) = 3. where a, b, c are non zero real numbers. Then the value of ab(a + b) + bc (b + c) + ca (a + c) is ………………………..
A) 0
B) 2
C) 1
D) 3
Answer:
A) 0

Question 68.
If \(\sqrt{15-x \sqrt{14}}=\sqrt{8}-\sqrt{7}\) then x = …………………….
A) 1
B) 0
C) 3
D) 4
Answer:
D) 4

Question 69.
If 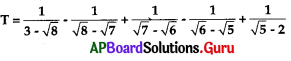then …………………..
A) T < 1
B) T = 1
C) T > 2
D) 1 < T < 2
Answer:
C) T > 2

Question 70.
If a^x = b^y – c^z and b² = ac then y = ………………….
A) \(\frac{\mathrm{xz}}{\mathrm{x}+2}\)
B) \(\frac{\mathrm{XZ}}{2(\mathrm{x}-\mathrm{z})}\)
C) \(\frac{\mathrm{xz}}{2(\mathrm{z}-\mathrm{x})}\)
D) \(\frac{2 \mathrm{xz}}{(\mathrm{x}+\mathrm{z})}\)
Answer:
D) \(\frac{2 \mathrm{xz}}{(\mathrm{x}+\mathrm{z})}\)

Question 71.
If the ratio of the ages of Mona and Sona is 4:5 and twelve years hence their ages will be in the ratio of 5 : 6, then the age of Sona after 6 years will be …………………
A) 66 years
B) 55 years
C) 67 years
D) 77 years
Answer:
A) 66 years

Question 72.
In a zoo, there are Rabbits and Pigeons. If their heads are 90 and their legs are 224. Then the number of Pigeons in the zoo is ………………….
A) 70
B) 68
C) 72
D) 22
Answer:
B) 68

Question 73.
If x = \(\sqrt{-1+4 \sqrt{3}}\) then x + \(\frac{1}{x}\) = ……………………
A) 4
B) 6
C) 3
D) 2
Answer:
C) 3

Question 74.
The value of \(\frac{1}{2+\sqrt{3}}+\frac{1}{2-\sqrt{3}}\) is ……………………..
A) 3
B) 4
C) 5
D) 1
Answer:
B) 4

Question 75.
If x = \(\frac{2}{3+\sqrt{7}}\) then (x – 3)² = ………………..
A) 1
B) 4
C) 3
D) 8
Answer:
D) 8

Question 76.
If \(\frac{4+3 \sqrt{3}}{2+\sqrt{3}}\) = a + √b then (a, b) = …………………….
A) (12, 1)
B) (-1, 12)
C) (-12, -1)
D) (-12,1)
Answer:
B) (-1, 12)

Question 77.
If \(\frac{\sqrt{7}-\sqrt{3}}{x}=\frac{x}{\sqrt{7}+\sqrt{3}}\) then the value of x = …………………….
A) 11
B) 2
C) 16
D) 12
Answer:
B) 2

Question 78.
If p³ + q³ + r³ then log_pr – q + log_p(r² + qr + q²) ………………..
A) 3
B) 8
C) 9
D) 14
Answer:
A) 3

Question 79.
= …………………..
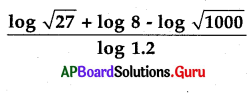A) 10.52
B) 1.5
C) 3.5
D) 20.5
Answer:
B) 1.5

Question 80.
\(\frac{1}{\log _{2} \cdot \log _{2} \cdot \log _{2} 16}\) = ………………….
A) 1
B) 5
C) 6
D) 8
Answer:
A) 1

Question 81.
If log(x + y) = log(\(\frac{3 x-3 y}{2}\)) then log x – log y = …………………….
A) log 6
B) log 3
C) log 5
D) log 2
Answer:
C) log 5

Question 82.
If log [latex]\frac{x+y}{3}[/latex] = \(\frac{1}{2}\) [log x + log y] then \(\frac{x}{y}+\frac{y}{x}\) = ………………..
A) 8
B) 7
C) 10
D) 9
Answer:
B) 7

Question 83.
If log₁₀3 = 0.4771, then the value of log 15 + log 2 = ………………….
A) 1.4771
B) 47.71
C) 4.77
D) 0.4771
Answer:
A) 1.4771

Question 84.
Find the value of \(\log _{\frac{4}{3}} \frac{256}{81}\)
A) 1
B) 8
C) 2
D) 4
Answer:
D) 4

Question 85.
(X^a. X^b)^{a – b}(X^b. X^c)^{b – c}(x^c. X^a)^{c – a} = …………………..
A) 0
B) 1
C) ∞
D) 2
Answer:
B) 1

Question 86.
If \(x^{1-\log _{5}^{x}}\) = 0.04 then x = ………………..
A) 5, \(\frac{1}{25}\)
B) \(\frac{1}{5}\), 25
C) 25, 5
D) \(\frac{1}{5}, \frac{1}{25}\)
Answer:
B) \(\frac{1}{5}\), 25

Question 87.
If log₁₀343 = 2.5353, then the least positive integer ‘n’ such that 7ⁿ > 10⁵ is
A) 6
B) 1
C) 4
D) 5
Answer:
A) 6

Question 88.
If x² + y² = 6xy then 2 log(x + y)-log(xy) = …………………
A) log 2
B) 2 log 2
C) 3 log 2
D) 4 log 2
Answer:
C) 3 log 2

Question 89.
\(\frac{4}{9^{\frac{1}{3}}-3^{\frac{1}{3}}+1}=\mathbf{A} \cdot 3^{\frac{1}{3}}\) + B then
A) A = 2
B) A = 3
C) B = 1
D) B = 2
Answer:
C) B = 1

Question 90.
x = 3 + 2√2 then x⁴ + \(\frac{1}{x^{4}}\) = ……………….
A) 1152
B) 1053
C) 1154
D) 1159
Answer:
C) 1154

Question 91.
x = \(\frac{\sqrt{2}+1}{\sqrt{2}-1}\) , y = \(\frac{\sqrt{2}-1}{\sqrt{2}+1}\) then x² – xy + y² = …………………..
A) 33
B) 37
C) 36
D)49
Answer:
A) 33

Question 92.
\(\sqrt[3]{a}+\sqrt[3]{b}+\sqrt[3]{c}\) = 0 then (a + b + c)³ = ……………….
A) 3 abc
B) 9 abc
C) 27 abc
D) 81 abc
Answer:
C) 27 abc

Question 93.
Rationalising factor of \(\sqrt[3]{16}-\sqrt[3]{4}\) + 1 is …………………….
A) \(\sqrt[3]{4}\) + 2
B) \(\sqrt[3]{4}\) – 2
C) \(\sqrt[3]{4}\) + 1
D) \(\sqrt[3]{4}\) – 1
Answer:
C) \(\sqrt[3]{4}\) + 1

Question 94.
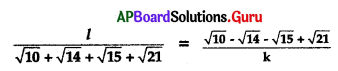then k = ……………………..
A) k = \(\frac{l}{2}\)
B) l = \(\frac{2}{k}\)
C) l = \(\frac{\mathrm{k}}{2}\)
D) K = \(\frac{2}{l}\)
Answer:
B) l = \(\frac{2}{k}\)

Question 95.
A rationalising factor of \(\sqrt[3]{25}+\frac{1}{\sqrt[3]{25}}-1\) is …………………
A) \(5^{\frac{1}{3}}-5^{\frac{1}{3}}\)
B) \(5^{\frac{1}{3}}+5^{\frac{1}{3}}\)
C) \(25^{\frac{1}{3}}+25^{\frac{-1}{3}}\)
D) \(25^{\frac{1}{3}}-25^{\frac{-1}{3}}\)
Answer:
B) \(5^{\frac{1}{3}}+5^{\frac{1}{3}}\)

Question 96.
\(\frac{\sqrt{x^{2}+1}+\sqrt{x^{2}-1}}{\sqrt{x^{2}+1}-\sqrt{x^{2}-1}}\) + \(\frac{\sqrt{x^{2}+1}-\sqrt{x^{2}-1}}{\sqrt{x^{2}+1}+\sqrt{x^{2}-1}}\)
A) 3x²
B) 2x²
C) 2x
D) 4x²
Answer:
B) 2x²

Question 97.
Arithmetic mean of two surds is 5 +9√2 and one of them is 1 + 12√2 then second surd is ……………….
A) 7 + 6√2
B) 9 + 6 √2
C) 10 + 6√2
D) 8 + 6√2
Answer:
B) 9 + 6 √2

Question 98.
\(\frac{1+\sqrt{2}}{3-2 \sqrt{2}}\) = a + b√2 then (a, b) = ……………………
A) (7, 5)
B) (-7, 5)
Q (3, 5)
D) (-7, -5)
Answer:
A) (7, 5)

Question 99.
x = 2√2 + √7 then \(\frac{1}{2}\left(x-\frac{1}{x}\right)\) = …………………
A) √2
B) √7
C) √8
D) 2√7
Answer:
B) √7

Question 100.
If the product of two irrational numbers is rational, then which of the following can be concluded ?
A) The ratio of the greater and the smaller numbers is an integer.
B) The sum of the numbers must be rational.
C) The excess of the greater irrational number over the smaller irrational number must be rational.
D) The sum of the numbers must be irrational
Answer:
D) The sum of the numbers must be irrational

Question 101.
Which of the following is always true?
A) The product of two distinct . irrational numbers is irrational.
B) The rationalising factor of a number is unique.
C) The sum of two distinct irrational numbers is rational.
D) None of these
Answer:
D) None of these

Question 102.
Which of the following pair of numbers is co-prime ?
A) 8 and 14
B) 6 and 35
C) 4 and 12
D) 9 and 19
Answer:
B) 6 and 35

Question 103.
Which of the following is not an irrational number ?
A) √2
B) √9
C) √3
D) √7
Answer:
B) √9

Question 104.
Which of the following is a rational number ?
A) √2
B) π
C) \(\frac{1}{3}\)
D) √3
Answer:
C) \(\frac{1}{3}\)

Question 105.
Which of the following four digit numbers is a perfect square such that the first two digits and the last two digits considered separately also represent perfect squares ?
A) 1681
B) 5462
Q 8214
D) 7210
Answer:
A) 1681

Question 106.
The solution of which equation is an irrational number ?
A) \(\frac{1}{x}=\frac{3}{4}\)
B) x² = \(\frac{49}{20}\)
C) \(\frac{1}{2} x+\frac{1}{5}=\frac{1}{3}\)
D) ² = \(\frac{9}{16}\)
Answer:
B) x² = \(\frac{49}{20}\)

Question 107.
Which of the following is always true?
A) Every irrational number is a surd.
B) Any surd of the form n√a + n√b can be rationalised by a surd of the form n√a -n√b where n√a and n√b are surds.
C) Both (A) and (B)
D) Neither (A) nor (B)
Answer:
D) Neither (A) nor (B)

Question 108.
Among the following a rational number is ………………
A) 1.121212 ……………..
B) 1.23874 ………………
C) 0.23567 ……………….
D) 0.1785 ………………
Answer:
B) 1.23874 ………………

Question 109.
If log₃2 log₃(2^x – 5) log₃(2^x – \(\frac{7}{2}\)) are in A.P then x is
A) an odd positive integer
B) a positive fraction
C) an even positive integer
D) an odd positive integer or even positive integer
Answer:
A) an odd positive integer

Question 110.
If n is an odd natural number, 3²ⁿ + 2²ⁿ is always divisible by ………………
A) 13
B) 15
C) 17
D) 19
Answer:
A) 13

Question 111.
Given that the units digit of A³ and A are the same where A is a single digit natural number. How many possibilities can A assume ?
A) 3
B) 4
C) 5
D) 9
Answer:
C) 5

Question 112.
The remainder of any perfect square divided by 3 is
A) 0
B) 1
C) either (A) or (B)
D) neither (A) nor (B)
Answer:
C) either (A) or (B)

Question 113.
The LCM and HCF of two numbers are equal, then the numbers must be ……………….
A) prime
B) co-prime
C) composite
D) equal
Answer:
D) equal

Question 114.
n² – 1 is divisible by 8, if n is ……………………..
A) an odd number
B) an even number
C) prime number
D) integer
Answer:
A) an odd number

Question 115.
If n is a natural number, then which of the following expression ends with zero ?
A) (3 × 2)ⁿ
B) (5 × 7)ⁿ
C) (9 × 3)ⁿ
D) (2 × 5)ⁿ
Answer:
D) (2 × 5)ⁿ

Question 116.
The decimal expansion of \(\frac{9}{17}\) is …………………….
A) Terminating
B) Non-terminating and non-repeating
C) Non-terminating and repeating
D) Terminating and repeating
Answer:
C) Non-terminating and repeating

Question 117.
If n is any natural number then 6ⁿ – 5ⁿ always ends with …………………
A) 1
B) 5
C) 8
D) 7
Answer:
A) 1

Question 118.
If 6a53435 is divisible by both 5 and 3, then the least possible value of ‘a’ is ……………..
A) 1
B) 0
C) 2
D) 3
Answer:
A) 1

Question 119.
If a = 2 + √3 and b = 2 – √3 then a + b is ………………….
A) Rational
B) Irrational
C) 0
D) Natural
Answer:
B) Irrational

Question 120.
The multiplicative inverse does not exist in the set of ………………..
A) Natural numbers
B) Whole numbers
C) Integers
D) All
Answer:
D) All

Question 121.
Logarithmic form of 10³ = 1000
A) log₁₀¹⁰⁰⁰ = 3
B) log₃¹⁰ = 3
C) log₁₀³ = 3
D) None
Answer:
A) log₁₀¹⁰⁰⁰ = 3

Question 122.
\((\sqrt[m]{\sqrt[n]{a b}})^{\min }\) = ………………..
A) abⁿ
B) ab^m
C) a^mb
D) ab
Answer:
D) ab

Question 123.
If n is a natural number, then 9²ⁿ – 4²ⁿ is always divisible by…………………..
A) 5
B) 13
C) either (A) or (B)
D) neither (A) nor (B)
Answer:
C) either (A) or (B)

Question 124.
N is a natural number such that when ‘N is divided by N’, it leaves remainder a. It can be concluded that ………………….
A) a is a perfect cube
B) a is a perfect square
C) a is a perfect square and cube
D) neither (A) nor (B)
Answer:
A) a is a perfect cube

Question 125.
There is a circular path around a sports field. Anand takes 18 minutes to drive one round of the field while Prakash takes 12 minutes for the same. Suppose they both start at the same point and at the same time and go in the same direc¬tion. After how many minutes will they meet again at the starting point ?
A) 36 minutes
B) 19 minutes
C) 48 minutes
D) 56 minutes
Answer:
A) 36 minutes

Question 126.
A sweet seller has 420 Kaju burfies and 130 Badam burfies. She wants to stock them in such a way that each stock has the same number and they take up the least area of the tray. What is the number of burfies that can be placed in each stock for this purpose ?
A) 15
B) 10
C) 40
D) 45
Answer:
B) 10

Question 127.
In a seminar, the number of participants in English, Mathematics and Science are 36, 60 and 84 respectively. Find the minimum number of rooms required if in each room the same number of participants are to be seated and all of them being in the same subject.
A) 15
B) 28
C) 40
D) 18
Answer:
A) 15

Question 128.
Ramu has two vessels which contain 720 ml and 405 ml of milk respectively. Milk in each vessel is poured into glasses of equal capacity to their brim. Find the minimum number of glasses which can be filled with milk.
A) 25
B) 36
C) 48
D) 65
Answer:
A) 25

Question 129.
A student is ranked 9^th from the top and 38^th from the bottom in a class. The number of students in the class is ………………
A) 46
B) 48
C) 45
D) 49
Answer:
A) 46

Question 130.
In a group of elephants and ducks if the number of legs are 24 more than twice the number of heads, then the number of elephants in the group is …………………
A) 6
B) 12
C) 8
D) 16
Answer:
B) 12

Question 131.
The sum of seven numbers is 235. If the average of the first three numbers is 23 and that of the last three numbers is 42, then the fourth number is ……………….
A) 120
B) 66
C) 40
D) 195
Answer:
C) 40

Question 132.
If a two digits number is divisible by 3 and 4, also the difference between the unit’s digit and the ten’s digit is equal to 4, then the number is ………………..
A) 96
B) 48
C) 72
D) 36
Answer:
B) 48

Question 133.
Complete the missing entries in the following factor tree.

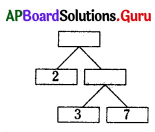
A) 42,21
B) 61, 71
C) 21,46
D) 21,48
Answer:
A) 42,21

Question 134.
Identify the factors of 24.

Answer:

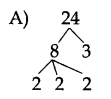
Question 135.
Which of the following may be the value of √2 on the number line

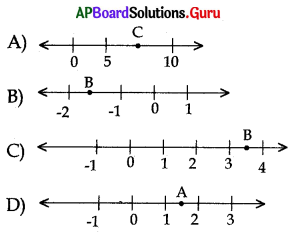
Answer:

Question 136.
Which of the following triangle was √2

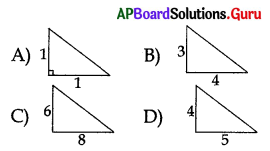
Answer:

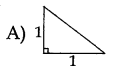
Question 137.
In between which two parts \(\frac{3}{4}\) can belocated in the number line

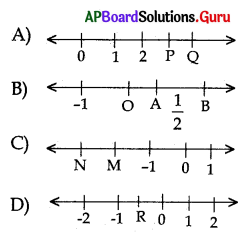
Answer: