Practice the AP 10th Class Maths Bits with Answers 12th Lesson త్రికోణమితి అనువర్తనాలు on a regular basis so that you can attempt exams with utmost confidence.
AP Board 10th Class Maths Bits 12th Lesson త్రికోణమితి అనువర్తనాలు
ప్రశ్న1.
ఒక స్థూపము యొక్క పొడవు, నీడల నిష్పత్తి 1 : √3 అయిన సూర్యుని ఊర్ధ్వకోణము విలువ ఎంత ?
జవాబు :
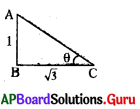
tan θ = [latex]\frac{\mathrm{AB}}{\mathrm{BC}}=\frac{1}{\sqrt{3}}[/latex]
θ = 30.
సూర్యుని కిరణాల ఊర్థ్వకోణం = 30°
ప్రశ్న2.
20 మీ. పొడవు గల నిచ్చెన 10 మీ. ఎత్తు వద్ద గోడను తాకుచు క్షితిజ సమాంతరంతో నిచ్చెన చేసే కోణమును కనుగొనుము.
జవాబు :
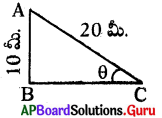
sin θ = [latex]\frac{\mathrm{AB}}{\mathrm{AC}}=\frac{10}{20}=\frac{1}{2}[/latex]
θ = 30°
ప్రశ్న3.
x మీ. పొడవు గల నిచ్చెన భూమితో ‘O’ కోణం చేయుచున్నట్లు గోడకు వేయబడింది. ఆ నిచ్చెన పాదం, గోడల మధ్య దూరాన్ని నేరుగా కనుక్కోవడానికి ఈ క్రిందివానిలో ఏ నిష్పత్తిని ఎంచుకుంటారు ?
A) sin θ
B) cos θ
C) tan θ
D) cot θ
జవాబు :
B) cos θ
ప్రశ్న4.
ఒక భవనం యొక్క అడుగుభాగం నుండి ‘d’ మీ. దూరంలో ఉన్న స్థానం నుండి భవనం యొక్క పై భాగంను ‘α’ ఊర్థ్వకోణంను చూస్తే భవనం ఎత్తును కనుగొనే సందర్భంలో ఈ క్రింది త్రికోణమితి నిష్పత్తులలో దీనిని ఉపయోగిస్తారు.
A) tan α
B) sin α
C) cos α
D) sec α
జవాబు :
A) tan α
ప్రశ్న5.
సూర్యుని ఊర్ధ్వకోణం 0° నుండి 90° పెరుగుతూ ఉంటే, స్థంభము యొక్క నీడ పొడవు _________
A) మార్పులేదు
B) పెరుగుతుంది
C) తగ్గుతుంది
D) చెప్పలేము
జవాబు :
C) తగ్గుతుంది
![]()
ప్రశ్న6.
12 మీ. ఎత్తు గల టవర్ పైభాగము నుండి నేలపై గల ఒక స్థలము 30°ల నిమ్నకోణాన్ని చేస్తుంది. నిమ్నకోణాన్ని చేసిన స్థానం నుండి టవర్ పై భాగానికి గల దూరం ఎంత ?
జవాబు :
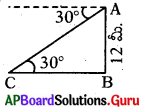
sin 30° = [latex]\frac{\mathrm{AB}}{\mathrm{AC}}=\frac{12}{\mathrm{AC}}[/latex]
⇒ [latex]\frac{1}{2}=\frac{12}{\mathrm{AC}}[/latex] ⇒ AC = 24 మీ.
నిమ్నకోణాన్ని చేసిన స్థానం C నుండి టవరుపై భాగం A కు గల దూరం = 24 మీ. .
ప్రశ్న7.
సూర్యకిరణాలు భూమితో చేయు ఊర్ధ్వ కోణము 45° అయినపుడు 12 మీ. ఎత్తు గల చెట్టు ఏర్పరచు నీడ పొడవును కనుగొనుము.
జవాబు :
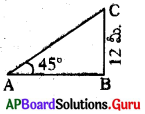
చెట్టు పొడవు = 12 మీ.
నీడ పొడవు AB.
tan 45° = [latex]\frac{\mathrm{BC}}{\mathrm{AB}}=\frac{12}{\mathrm{AB}}[/latex]
1 =[latex]\frac{12}{\mathrm{AB}}[/latex] ⇒ AB = 12 మీ.
∴ నీడ పొడవు = 12 మీ.
ప్రశ్న8.
క్రింద ఇవ్వబడిన పటం నుండి నిచ్చెన సారమును లెక్కించండి.
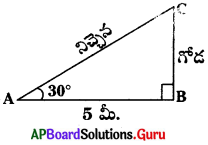
జవాబు :
cos 30° = [latex]\frac{\mathrm{AB}}{\mathrm{AC}}=\frac{5}{\mathrm{AC}} \Rightarrow \frac{\sqrt{3}}{2}=\frac{5}{\mathrm{AC}}[/latex]
నిచ్చెన పొడవు AC = [latex]\frac{10}{\sqrt{3}}[/latex]మీ.
ప్రశ్న9.
క్రింది పటములో BC ను కనుగొనుము.
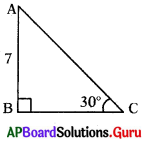
జవాబు :
tan 30° = [latex]\frac{\mathrm{AB}}{\mathrm{BC}}=\frac{20}{20}[/latex] = 1
⇒ BC = 7√3 యూనిట్లు .
ప్రశ్న10.
20 మీ. ఎత్తు గల ఒక స్తంభం పై భాగాన్ని, బాస్ పాదం నుండి 20 మీ. దూరములో గల ఒక బాలుడు పరిశీలించినపుడు ఏర్పడు ఊర్ధ్వకోణం కోణము ఎంత?
జవాబు :
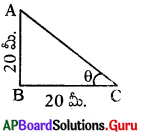
tan θ = [latex]\frac{\mathrm{AB}}{\mathrm{BC}}=\frac{20}{20}[/latex] = 1
θ = 45°
ప్రశ్న11.
ఒక స్తంభం నీడ పొడవు, స్తంభం పొడవుతో సమానంగా వుంటే, స్థంభం సూర్యునితో చేయు ఊర్ధ్వకోణం 45° అని చూపుము.
జవాబు :
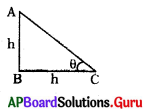
AB స్తంభం ఎత్తు = BC నీడ పొడవు
tan θ = [latex]\frac{\mathrm{AB}}{\mathrm{BC}}=\frac{\mathrm{h}}{\mathrm{h}}[/latex] = 1
tan θ = 1
∴ θ = 45°
ప్రశ్న12.
20 మీ. పొడవు గల నిచ్చెన భూమితో 2 కోణం చేస్తూ 10మీ. పొడవు గల స్థంభంనకు వేయబడినది. అయిన a విలువ ఎంత ?
జవాబు :
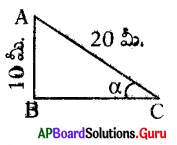
sin α = [latex]\frac{\mathrm{AB}}{\mathrm{AC}}=\frac{10}{20}=\frac{1}{2}[/latex]
∴ α = 30°
ప్రశ్న13.
ఒక చెట్టు యొక్క నీడ పొడవు 8 మీ. మరియు అది 45°ల కోణము చేయుచున్న దాని పొడవు
జవాబు :
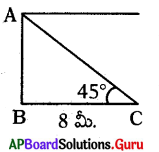
tan 45° = [latex]\frac{\mathrm{AB}}{\mathrm{BC}}=\frac{\mathrm{AB}}{8}[/latex]
1 = [latex]\frac{\mathrm{AB}}{8}[/latex]
∴ చెట్టు ఎత్తు AB = 8 మీ.
ప్రశ్న14.
6 మీ. పొడవు గల స్తంభం యొక్క. నీడ 2√3 మీ. అయిన, ‘సూర్యకిరణాలు భూమితో చేయు కోణము ఎంత ?
జవాబు :
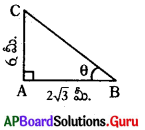
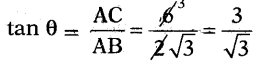
tan θ = √3
∴ θ = 60°
∴ సూర్యకిరణాలు భూమితో చేయు కోణము = 60°
ప్రశ్న15.
ఒక టవరు అడుగు భాగం నుండి 100 మీ. దూరంలో కలు బిందువు టవరుపై నుండి 60° నిమ్నకోణాన్ని “స్తున్నది. అయితే ఆ టవరు ఎత్తు ఎంత ?
జవాబు :
∆ABCలో
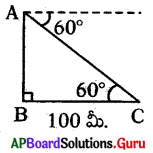
tan 60° = [latex]\frac{\mathrm{AB}}{\mathrm{BC}}=\frac{\mathrm{AB}}{100}[/latex]
√3 = [latex]\frac{\mathrm{AB}}{100}[/latex]
60° = AB = 100√3
∴ టవరు ఎత్తు AB = 100√3 మీ.
ప్రశ్న16.
ఒక టవరు ఎత్తు. 10 మీటర్లు, అది సూర్యునితో 45° కోణము చేయుచున్న దాని నీడ పొడవు ఎంత ?
జవాబు :
నీడ పొడవు = 10 మీ.
(∵ కోణము 45° అయిన టవరు ఎత్తు = వీడ పొడవు)
![]()
ప్రశ్న17.
ఒక టవరు నీడ, దాని పొడవుకు √3 రెట్లు అయిన ఆ టవరు సూర్యునితో ఏర్పరచు కోణము ఎంత ?
జవాబు :
tan θ = [latex]\frac{\mathrm{AB}}{\mathrm{BC}}=\frac{\mathrm{x}}{\sqrt{3} \mathrm{x}}=\frac{1}{\sqrt{3}}[/latex]
∴ θ = 30°
టవరు సూర్యునితో చేయు కోణము = 30°
ప్రశ్న18.
పటంలో పరిశీలన స్థానము, వస్తువులు గుర్తించబడినవి అయిన నిమ్న కోణము విలువను తెల్పండి.
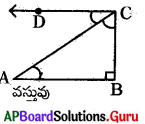
జవాబు :
సాధన. నిమ్న కోణం = ∠DCA
ప్రశ్న19.
పటంలో θ విలువ ఎంత?
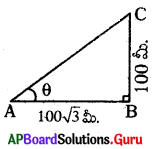
జవాబు :
tan θ = [latex]\frac{100}{100 \sqrt{3}}=\frac{1}{\sqrt{3}}[/latex] ⇒ θ = 30°
ప్రశ్న20.
X మరియు Yఎత్తులు గల రెండు టవర్లు వాటి మధ్య బిందువు నుండి 30° మరియు 60°ల ఊర్ద్వకోడాలను ఏర్పరచిన X :Y విలువ ఎంత ?
జవాబు :
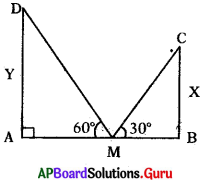
AM = MB
∆CBM లో
tan 30° = [latex]\frac{C B}{B M}=\frac{X}{B M} \Rightarrow \frac{1}{\sqrt{3}}=\frac{X}{B M}[/latex]
⇒ X = [latex]\frac{\mathrm{BM}}{\sqrt{3}}[/latex] …………(1)
∆DAM లో
tan 60° = [latex]\frac{\mathrm{DA}}{\mathrm{AM}}=\frac{\mathrm{Y}}{\mathrm{AM}}[/latex] ⇒ √3 = [latex]\frac{\mathbf{Y}}{\mathbf{A M}}[/latex]
⇒ Y = √3 AM ………. (2)
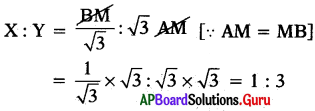
ప్రశ్న21.
నిమ్నకోణాన్ని నిర్వచించండి.
జవాబు :
నిమ్నకోణము : క్షితిజ సమాంతర రేఖకు, దృష్టి రేఖ క్రింద ఉన్నప్పుడు వాని మధ్య ఏర్పడే కోణాన్ని నిమ్న కోణము అంటారు.
ప్రశ్న22.
సూర్యునితో 60° కోణమును ఏర్పరచు, 6 మీ. పొడవు గల స్థూపము యొక్క నీడ పొడవు ఎంత ?
జవాబు :
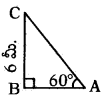
tan60° = [latex]\frac{\mathrm{CB}}{\mathrm{AB}}=\frac{6}{\mathrm{AB}}[/latex]
= √3 = [latex]\frac{6}{\mathrm{AB}}[/latex]
నీడ పొడవు AB = [latex]\frac{6}{\sqrt{3}}[/latex] మీ.
ప్రశ్న23.
12 మీ. ఎత్తు గల ఒక స్థూపము 4√3 మీ. పొడవు గల నీడను ఏర్పరచిన సూర్యునితో అది ఏర్పరచు కోణము విలువ ఎంత ?
జవాబు :
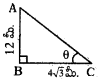
θ = 60°
– సూర్యకిరణాలు భూమితో 60° చేయును.
ప్రశ్న24.
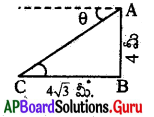
ఇచ్చిన పటంలో A అను పరిశీలన .బిందువు నుండి – ‘C’ ను గమనించగా A వద్ద ఏర్పరచు నిమ్న కోణము విలువ ఎంత?
జవాబు :
θ = ∠C, tan C = [latex]\frac{4}{4 \sqrt{3}}=\frac{1}{\sqrt{3}}[/latex]
∴ C = θ = 30°
∴ నిమ్న కోణం θ = 30°
ప్రశ్న25.
ఒక వ్యక్తి యొక్క నీడ, అతని పొడవులు. సమానము అయిన సూర్యుని కిరణాలు భూమితో చేయు కోణము ఎంత ?
జవాబు :
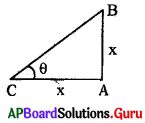
tan θ = [latex]\frac{\mathbf{X}}{\mathbf{X}}[/latex] = 1
θ = 45°
∴ సూర్యకిరణాలు భూమితో చేయు కోణము = 45°
ప్రశ్న26.
ఒక టవరు యొక్క నీడ పొడవు, దాని ఎత్తుకు [latex]\frac{1}{\sqrt{3}}[/latex] రెట్లు ఉన్న సూర్యకిరణాలు ఆ సమయంలో భూమితో చేయు కోణము ఎంత ?
జవాబు :
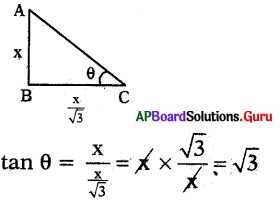
∴ సూర్యకిరణాలు భూమితో చేయు కోణము మన = θ = 60°.
![]()
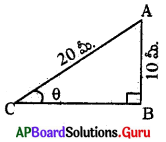
ప్రశ్న27.
కింద ఇవ్వబడిన పటంలో, AB = 10 మీ. మరియు AC = 20 మీ. అయిన 6 విలువ ఎంత ?
జవాబు :
sin θ = [latex]\frac{10}{20}=\frac{1}{2}[/latex]
θ = 30°
ప్రశ్న28.
6 మీటర్ల పొడవు గల స్తంభము 2√3 మీటర్ల పొడవు గల నీడను ఏర్పరచిన, సూర్యుని ఊర్ధ్వ కోణము విలువ ఎంత ?
జవాబు :
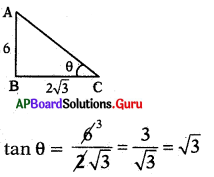
∴ θ = 60.
∴ సూర్యుని ఊర్ధ్వకోణం = 60
ప్రశ్న29.
క్రింది పటంలో, AB = CD = 10√3 మీ. అయిన BC విలువ ఎంత ?
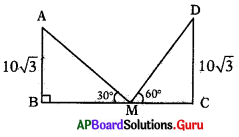
జవాబు :
∆ABM లో .
tan 30° = [latex]\frac{\mathrm{AB}}{\mathrm{BM}} \Rightarrow \frac{1}{\sqrt{3}}=\frac{10 \sqrt{3}}{\mathrm{BM}}[/latex]
BM = 10√3 × √3 = 30 మీ.
∆DCM లో
tan 60° = [latex]\frac{\mathrm{CD}}{\mathrm{MC}}=\frac{10 \sqrt{3}}{\mathrm{MC}}[/latex]
√3 = [latex]\frac{10 \sqrt{3}}{\mathrm{MC}}[/latex] ⇒ MC = 10 మీ.
BC = BM + MC = 30 + 10 = 40 మీ.
ప్రశ్న30.
క్రింది పటంలో, AB = 10√3 మీ. అయిన CD = _________ మీ.
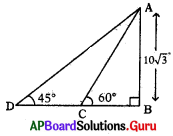
A) 10(√3 + 1)
B) 10√3
C) [latex]\frac{10}{\sqrt{3}}[/latex]
D) 10(√3 – 1)
జవాబు :
D) 10(√3 – 1)
∆ABDలో BD = BA = 10√3 (∵ AD = 459)
∆ABCE tan 60° = [latex]\frac{10 \sqrt{3}}{\mathrm{BC}}[/latex] = √3 = [latex]\frac{10 \sqrt{3}}{\mathrm{BC}}[/latex]
BC = 10
CD = BD – BC = 10√5 – 10
= 100(√3 – 1)మీ.
ప్రశ్న31.
నిమ్నకోణాన్ని సూచించే పటాన్ని గీయండి.
జవాబు :
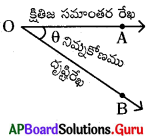
∠AOB నిమ్నకోణము.
ప్రశ్న32.
ఊర్థ్వకోణాన్ని నిర్వచించండి.
జవాబు :
ఊర్ద్వకోణము : క్షితిజ సమాంతర రేఖకు దృష్టిరేఖ పైన ఉన్నప్పుడు వాని మధ్య ఏర్పడే కోణాన్ని ఊర్థ్వకోణం అంటారు.
ప్రశ్న33.
ఊర్థ్వకోణాన్ని సూచించే పటాన్ని గీయండి.
జవాబు :
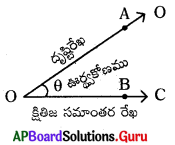
∠BOA ఊర్థ్వకోణము.
→ 100 మీ. పొడవు గల దారంతో ఎగురుతున్న ఒక గాలిపటం భూమితో 60° కోణము చేయుచున్నది.
పై సమాచారాన్ని చదివి 34, 35 ప్రశ్నలకు సమాధానాలు రాయండి.
ప్రశ్న34.
పై సమాచారాన్ని చూపు చిత్తుపటాన్ని గీయండి.
జవాబు :
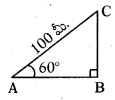
BC = గాలి పటం ఎత్తు
AC = దారం పొడవు = 100 మీ.
ప్రశ్న35.
భూమి నుండి గాలిపటం ఎంత ఎత్తులో కలదు ?
జవాబు :
sin 60° = [latex]\frac{\mathrm{BC}}{100} \Rightarrow \frac{\sqrt{3}}{2}=\frac{\mathrm{BC}}{100}[/latex]
BC = 100 × [latex]\frac{\sqrt{3}}{2}[/latex] = 50√3.
గాలిపటం భూమి నుండి 50√3 మీ. ఎత్తులో కలదు.
ప్రశ్న36.
ఒక టవరు ఎత్తుకు మరియు దాని నీడ పొడవుల నిష్పత్తి √3:1 అయిన సూర్యకిరణాలు భూమితో చేయు కోణము విలువ ఎంత ?
జవాబు :
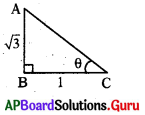
tan θ = [latex]\frac{\sqrt{3}}{1}[/latex]= √3
θ = 60°
సూర్యకిరణాలు భూమితో చేయు కోణం θ = 60°.
ప్రశ్న37.
ఒక గుడి అడుగు భాగం నుండి 100 మీ. దూరం నుండి గుడి శిఖరంను 30° ఊర్ధ్వకోణంతో చూచిన గుడి ఎత్తు ఎంత ?
జవాబు :
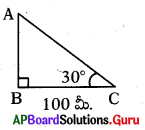
tan 30° = [latex]\frac{\mathrm{AB}}{100}[/latex]
[latex]\frac{1}{\sqrt{3}}=\frac{\mathrm{AB}}{100}[/latex]
గుడి ఎత్తు AB = [latex]\frac{100}{\sqrt{3}}[/latex] మీ.
ప్రశ్న38.
100√3 మీ. పొడవు గల సెల్ టవరు పైభాగాన్ని 100 మీ. దూరంలో గల ఒక పరిశీలనా స్థానం నుంచి చూచినచో ఊర్ధ్వ కోణమును కనుగొనుము.
జవాబు :
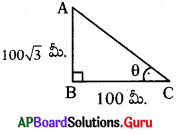
tan θ = 100√3
θ = 60°
ప్రశ్న39.
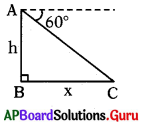
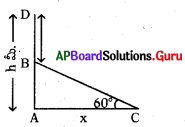
ఒక పర్వత శిఖరంపై నుండి శిఖరానికి ఒకే వైపుగల , రెండు వరుస కిలోమీటర్ల రాళ్ళను 45°, 30° లతో ‘ చూచిన పర్వత శిఖరం ఎత్తు ఎంత ?
జవాబు :
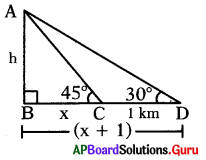
∆ABC లో
tan 45° = [latex]\frac{h}{x}[/latex] ⇒ 1 = [latex]\frac{h}{x}[/latex] ⇒ h = x …. (1)
∆ABD లో
tan 30° = [latex]\frac{\mathrm{h}}{\mathrm{x}+1} \Rightarrow \frac{1}{\sqrt{3}}=\frac{\mathrm{h}}{\mathrm{x}+1}[/latex]
⇒ h√3 = x + 1
⇒ h√3 = h + 1 [∵ h = x]
⇒ h(√3 – 1) =1
⇒ h = [latex]\frac{1}{\sqrt{3}-1}[/latex] కి.మీ.
∴ శిఖరం ఎత్తు = [latex]\frac{1}{\sqrt{3}-1}[/latex] కి.మీ.
![]()
ప్రశ్న40.
భూమి నుండి 7 కి.మీ. ఎత్తులో ఎగురుతున్న విమానం నుండి, విమానానికి ఒకేవైపు భూమిపై గల రెండు వరుస కిలోమీటరు రాళ్ళు 609, 45° ల నిమ్నకోణం చేస్తున్నాయి. పై సమాచారాన్ని పటంలో చూపండి.
జవాబు :
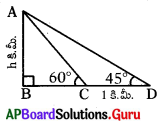
AB – భూమి నుండి విమానం ఎత్తు
CD – రెండు వరుస కి.మీ., రాళ్ళ మధ్య దూరం = 1 కి.మీ.
ప్రశ్న41.
w మీ. వెడల్పు గల రోడ్డు ఒక వైపునుండి మరొక వైపు 4 మీ. ఎత్తు గల భవనం పై భాగాన్ని 45° ఊర్వకోణంతో చూచిన w, hల మధ్య సంబంధమును తెల్పండి.
జవాబు :
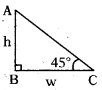
w = h
[∵ tan 45 = [latex]\frac{h}{w}[/latex] ⇒ 1= [latex]\frac{h}{w}[/latex] ⇒ h = w]
ప్రశ్న42.
h మీ. ఎత్తు గల పర్వత శిఖరం నుండి పర్వత అంచుల గుండా ప్రవహించే నదికి అవతలవైపు గల ఒక స్థానాన్ని 60° నిమ్మకోణంతో చూశారు. నది వెడల్పు x మీ. అయిన శ్రీ మరియు x ల మధ్య సంబంధమును రాయండి.
జవాబు :
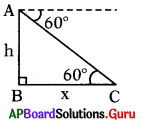
∆ABC లో
tan 60° = [latex]\frac{h}{w}[/latex]
= √3 = [latex]\frac{h}{w}[/latex]
∴ h = √3x
ప్రశ్న43.
h మీ. ఎత్తు గల పర్వత శిఖరం నుండి పర్వత అంచుల గుండా ప్రవహించే నదికి అవతలవైపు గల ఒక స్థానాన్ని 60° నిమ్నకోణంతో చూశారు. నది వెడల్పు x మీ. అయిన స్త్రీ మరియు x ల మధ్య సంబంధమును సరియగు పటం ద్వారా చూపండి.
జవాబు :
AB = పర్వత శిఖరము ఎత్తు = h మీ.
BC = నది వెడల్పు = x మీ.
ప్రశ్న44.
పై పటంలోని నిమ్నకోణాన్ని గుర్తునుపయోగించి రాయండి.
జవాబు :
నిమ్నకోణం = ∠AOB
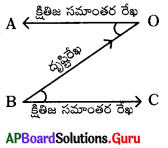
ప్రశ్న45.
క్రింది పటంలో AD = h మీ., BD = BC = y మీ., AC = x మీ., ∠ACB = 45° అయిన x, y మరియు h ను x, y లలో తెల్పండి.
జవాబు :
tan 45° = [latex]\frac{\mathrm{AB}}{\mathrm{AC}}[/latex] ⇒ 1 = [latex]\frac{\mathrm{AB}}{\mathrm{x}}[/latex] ⇒ AB = x
AD = AB + BD
h = x + y
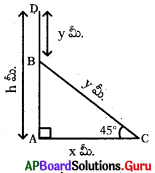
ప్రశ్న46.
క్రింది పటంలో AD = h మీ., BD = BC = y మీ. AC = x మీ. మరియు ∠ACB = 30° అయిన h ను x లలో రాయండి.
జవాబు :

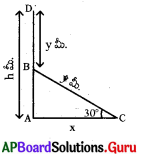
ప్రశ్న47.
46వ ప్రశ్నలో ACB = 60° అయిన h ను x లో రాయండి.
జవాబు :
tan 60° = [latex]\frac{\mathrm{AB}}{\mathrm{AC}}[/latex] = √3= [latex][/latex]
AB = √3x ………….. (1)
అలాగే cos 60° = [latex][/latex]
y = 2x …… (2)
h = AB + BD
= √3x + y = √3x + 2x
∴ h= (√3 + 2)x.
ప్రశ్న48.
1 మీ. పొడవు గల నిచ్చెన, 7 మీ. ఎత్తు వద్ద గోడతో 8 కోణం చేయుచున్నది. పై సందర్భాన్ని సూచించు పటాన్ని గీయండి.
జవాబు :
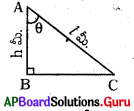
AC నిచ్చెన పొడవు = 1 మీ.,
AB గోడ ఎత్తు = h మీ.
→ క్రింది పటంలోని శంఖువు యొక్క శీర్షకోణము 609, వ్యాసార్ధం r = 7 సెం.మీ. అయితే క్రింది 49, 50 ప్రశ్నలకు సమాధానాలు రాయండి.
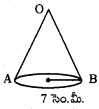
ప్రశ్న49.
శంఖువు ఏటవాలు ఎత్తు ఎంత ?
జవాబు :
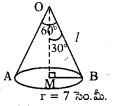
శంఖువు శీర్షకోణం ∠AOB = 60°
∆OMB లో ∠MOB = 30°
MB = r = 7 సెం.మీ.
sin 30° = [latex]\frac{\mathrm{MB}}{\mathrm{OB}} \Rightarrow \frac{1}{2}=\frac{7}{l}[/latex]
⇒ l = ఏటవాలు ఎత్తు = 14 సెం.మీ.
ప్రశ్న50.
శంఖువు ఎత్తు ఎంత ?
జవాబు :
∆OMB లో
tan 30° = [latex]\frac{\mathrm{MB}}{\mathrm{OM}} \Rightarrow \frac{1}{\sqrt{3}}=\frac{7}{\mathrm{OM}}[/latex]
⇒ OM = h = 7√3 సెం.మీ.
→ క్రింది పటంలోని నిమ్నకోణాన్ని పరిశీలించి, క్రింది 51-53 ప్రశ్నలకు సమాధానాలు రాయండి.
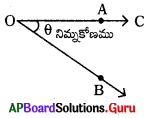
ప్రశ్న51.
దృష్టిరేఖను తెల్పండి.
జవాబు :
దృష్టిరేఖ [latex]\overrightarrow{\mathrm{OB}}[/latex].
![]()
ప్రశ్న52.
క్షిషితిజ సమాంతరరేఖ ఏది ?
జవాబు :
క్షితిజ సమాంతరరేఖ [latex]\overrightarrow{\mathrm{OA}}[/latex].
ప్రశ్న53.
పరిశీలనా స్థానం ఏది ?
జవాబు :
పరిశీలనా స్థానం : ‘O’.
ప్రశ్న54.
x మీ. పొడవు గల నిచ్చెనను భూమితో ‘B’ కోణం చేయునట్లు గోడకు వేయబడినది. ఆ నిచ్చెన పాదం మరియు గోడ పాదముల మధ్య దూరాన్ని నేరుగా కనుగొనుటకు నీవు, క్రింది వానిలో ఏ నిష్పత్తిని ఎన్నుకొంటావు ?
A) tan θ
B) sin θ
C) cos θ
D) cot θ
జవాబు :
C) cos θ
ప్రశ్న55.
x మీ. పొడవు గల నిచ్చెనను భూమితో ‘θ’ కోణం చేయునట్లు గోడకు వేయబడినది. నిచ్చెన గోడను తాకిన ఎత్తును నేరుగా కనుగొనుటకు సరైన నిష్పత్తి ఏది ?
జవాబు :
sin θ (లేదా) cosec θ
ప్రశ్న56.
ఒక నిచ్చెన భూమి నుండి X మీ. ఎత్తులో గల కిటికీని భూమితో, ‘θ’ కోణం చేయుచూ తాకుచున్నది. నిచ్చెన పొడవును నేరుగా కనుగొనుటకు నీవు ఈ క్రింది వానిలో ఏది సరైనదిగా భావిస్తున్నావు ?
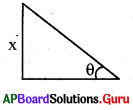
A) sin θ
B) cosec θ
C) sec θ
D) A లేదా C
జవాబు :
D) A లేదా C
ప్రశ్న57.
ఒక నిచ్చెన భూమి నుండి X మీ. ఎత్తులో గల కిటికీని భూమితో ‘θ’ చేయుచూ తాకుచున్నది. నిచ్చెన పాదము మరియు గోడ పాదముల మధ్య దూరమును నేరుగా కనుగొనుటకు సరైన త్రికోణమితీయ నిష్పత్తి.
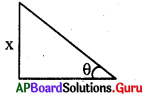
A) tan θ మాత్రమే
B) cot θ మాత్రమే
C) sin θ మాత్రమే
D) tan θ, cot θ లలో ఏదైనా
జవాబు :
D) tan θ, cot θ లలో ఏదైనా
ప్రశ్న58.
క్రింది పటంలో AB విమానం ఎత్తు X మీ., A పరిశీలకుని స్థానం, C సముద్రంలోని పడవ స్థానం అయిన, పరిశీలకుని నుండి పడవకు మధ్య గల దూరాన్ని (AC) ని నేరుగా కనుగొనుటకు సరైన త్రికోణమితీయ నిష్పత్తి.
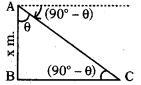
A) sin (90 – θ)
B) cos θ
C) A లేదా B
D ) cos (90 – θ)
జవాబు :
C) A లేదా B
ప్రశ్న59.
క్రింది పటంలో AB విమానం ఎత్తు X మీ., A పరిశీలకుని స్థానం; C సముద్రంలోని పడవ స్థానం అయిన, పరిశీలకుని నుండి పడవకు సముద్రంపై గల దూరము (BC) ని కనుగొనుటకు నీవు క్రింది వానిలో దేనిని ఎన్నుకొంటావు ?
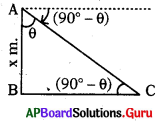
A) cos (90 – θ)
B) sin (90 – θ)
C) tan (90 – θ)
D) పైవన్నీ
జవాబు :
A) cos (90 – θ)
ప్రశ్న60.
x మీ. పొడవుగల నిచ్చెన భూమితో “0” కోణాన్ని చేస్తూ ఒక గోడను తాకుచున్నది. ఈ సమాచారాన్ని సూచించుటకు సరైన పటము.
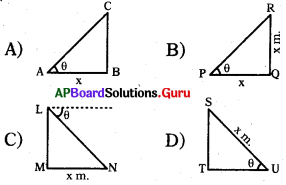
జవాబు :
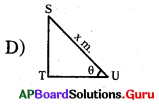
ప్రశ్న61.
క్రింది వానిలో నిమ్నకోణాన్ని సూచించు పటము
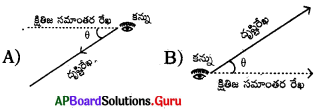
C) A మరియు B
D) ఏదీకాదు
జవాబు :
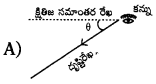
![]()
ప్రశ్న62.
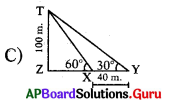
100 మీ. ఎత్తుగల టవర్ పై భాగాన్ని కిరణ్ 30° ఊర్వకోణంతో చూశాడు. ఆ తరువాత అదే సరళరేఖ వెంబడి టవర్ వైపునకు 40 మీ. నడచి టవర్ పై భాగాన్ని 60° ఊర్ధ్వకోణంతో చూచినచో పై సమాచారాన్ని సూచించు పటము
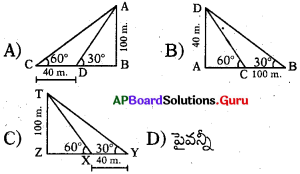
జవాబు :
ప్రశ్న63.
క్రింది వానిలో ఊర్ధ్వకోణాన్ని సూచించు పటము ,
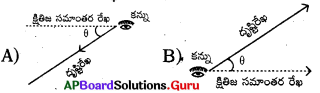
C) A మరియు B
D) ఏదీకాదు
జవాబు :
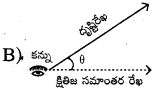
ప్రశ్న64.
క్రింది సంవర్గమాన విలువలకు సమానమవు త్రికోణమితీయ విలువలను జతపరచండి.
| i) log2√2 | a) cos 90° |
| ii) log22 | b) sin 90° |
| iii) log21 | c) cosec 30° |
| iv) log24 | d) sin 30° |
A) i-d, ii – b, iii – a, iv-c
B) i – c, ii – b, iii – a, iv-d
C) i-d, ii – a, iii – b, iv-c
D) i-b, ii -d, iii – a, iv-c
జవాబు :
A) i-d, ii – b, iii – a, iv-c
ప్రశ్న65.
క్రింది పటంలో నిచ్చెన పొడవును నేరుగా కనుగొనుటకు
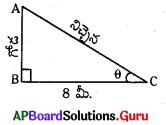
i) సరళ tan θ ను,
ii) పూర్ణిమ sin θ ను
iii)సురేష్ cos θ ను,
iv) ఖాదర్ cot θ ను ఎంచుకొన్నారు.
ఎవరి ఎంపిక సరైనదని నీవు భావిస్తున్నావు ?
జవాబు :
iii) సురేష్ ఎంపిక సరైనది.
ప్రశ్న66.
క్రింది పటంలో గోడ ఎత్తు నేరుగా కనుగొనుటకు
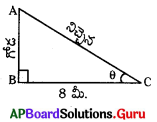
i) కిరణ్ sin θ ను,
ii) సాహీరా, tan θ ను,
iii)యశోద cot θ ను
iv) పద్మా cosec θ ను ఎంచుకొన్నారు.
పై ఎంపికలో ఏ ఇద్దరి ఎంపిక సరైనదని నీవు భావిస్తున్నావు ?
జవాబు :
సాహీరా, యశోదల ఎంపిక సరైనది.
ప్రశ్న67.
100 మీటర్ల పొడవైన ఒక టవర్ యొక్క నీడ పొడవు 100√3 మీటర్లు అయిన ఆ సమయంలో సూర్యునితో చేసే ఊర్ధ్వకోణమెంత ?
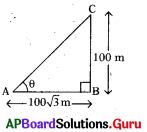
జవాబు :
∆ABC లో
tan θ = [latex]\frac{\mathrm{BC}}{\mathrm{AB}}[/latex] = tan θ = [latex]\frac{100}{100 \sqrt{3}}=\frac{1}{\sqrt{3}}[/latex]
θ = 30°
ప్రశ్న68.
క్రింది పటంలో ∠B = 90° అయిన నిమ్నకోణాన్ని తెలపండి.
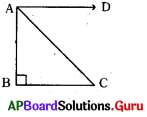
జవాబు :
∠DAC