AP 10th Class Maths Bits 11th Lesson త్రికోణమితి

Practice the AP 10th Class Maths Bits with Answers 11th Lesson త్రికోణమితి on a regular basis so that you can attempt exams with utmost confidence.

AP Board 10th Class Maths Bits 11th Lesson త్రికోణమితి

ప్రశ్న1.

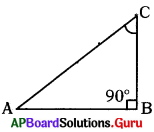
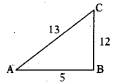
పై పటంలో sin C = \(\frac{3}{5}\) అయిన cos C విలువ. ఎంత ?
జవాబు :

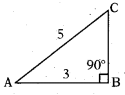
sin C = \(\frac{3}{5}\)
BC = 4 . 2.
(∵ 3, 4, 5 ప్రైథాగరియన్‌ త్రికాలు)
∴ cos C = \(\frac{\mathrm{BC}}{\mathrm{AC}}=\frac{4}{5}\)

ప్రశ్న2.
sin³θ.cos θ + cos³θ . sin θ = sin θ cos θ అని చూపుము.
జవాబు :
L.H.S = sin³θ cosθ + cos³θ sinθ
= sin θ cos θ (sin² θ + cos² θ)
= sin θ cos θ (1)
= sin θ cos θ = R.H.S.

ప్రశ్న3.
sin θ = cos θ అయిన విలువ ఎంత ? (0 < θ < 90)
జవాబు :
sin θ = cos θ అయిన
(cos 45 = sin 45 = \(\frac{1}{\sqrt{2}}\))
θ= 45°
(లేదా)
sin θ = cos θ ⇒ cos (90 – θ) = cos θ
∴ 90 – θ = 0 ⇒ 90 = 2θ
⇒ θ = \(\frac{90}{2}\) = 45°

ప్రశ్న4.
\(\frac{1}{\sec ^{2} A}+\frac{1}{{cosec}^{2} A}\) = 1 అని చూపుము
జవాబు :
L.H.S = \(\frac{1}{\sec ^{2} A}+\frac{1}{{cosec}^{2} A}\)
= cos² A + sin² A
= 1 = R.H.S.

ప్రశ్న5.
cos 60°. cos 30° + sin 60° . sin 30° విలువ ఎంత ?
జవాబు :
cos 60° · cos 30° + sin 60° : sin 30°

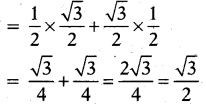
ప్రశ్న6.
tan θ cot θ = sec θ ·x అయిన x =
A) cos θ
B) sec θ
C) tan θ
D) cot θ
జవాబు :
A) cos θ

tan θ cot θ = sec θ . x
1 = sec θ . x
\(\frac{1}{\sec \theta}\) = x ⇒ x = cos θ.

ప్రశ్న7.
cos 1° . cos 2° . cos 3o ….. cos 180° యొక్క విలువ ఎంత ?
జవాబు :
cos 1°. cos 2°

ప్రశ్న8.
x = sin θ, y = cos θ అయిన sin θ, cos θ ల సర్వసమీకరణాన్నిx, y లలో రాయగా
A) x² – y² = 1
B) y² – x² = 1
C) x² + y² = 1
D) x² = y².
జవాబు :
C) x² + y² = 1
[∵ sin² θ + cos² θ = 1 :
⇒ x² + y² = 1]

ప్రశ్న9.
cos 12° – sin 78° విలువ ఎంత ?
జవాబు :
cos 12° – sin 78°
= cos 12° – sin (90° – 12)°
= cos 12° – cos 12° = 0

ప్రశ్న10.
x= cosec θ + cot θ; y = cosec θ – cot θ అయిన ఈ క్రింది వాటిలో సరైనది ………………….
A) x + y = 0
B) x – y = 0
C) \(\frac{x}{y}\) = 1
D) xy = 1
జవాబు :
D) xy = 1

(cosec θ + cot θ) (cosec θ – cot θ).
= cosec² θ – cot² θ = 1
∴ xy = 1

ప్రశ్న11.
cos (A – B) = ________
A) cos A cos B + sin A sin B
B) cos A sin A + cos B sin B
C) sin A sin B – cos A cos B
D) cos A cos B – sin A sin B
జవాబు :
A) cos A cos B + sin A sin B

ప్రశ్న12.
cos (90° – θ) = ________
జవాబు :
cos (90° – θ) = sin θ

ప్రశ్న13.
∆ABCలో of sin C = \(\frac{3}{5}\) అయిన విలువను కనుగొనుము
జవాబు :

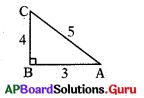
cos A = \(\frac{\mathrm{AB}}{\mathrm{AC}}=\frac{3}{5}\)

ప్రశ్న14.
tan² θ – sec² θ = ________
జవాబు :
tan² θ – sec² 0 = -(sec² – tan² A) = -1

ప్రశ్న15.
sec (90° – A) = ________
జవాబు :
sec (90° – A) = cosec θ

ప్రశ్న16.
cosec θ + cot θ = 5 అయిన cosec θ – cot θ విలువ ఎంత ?
జవాబు :
cosec² θ – cot² θ = 1
(cosec θ + cot θ) (cosec θ – cot θ) = 1
5(cosec θ – cot θ) = 1

∴ (cosec θ – cot θ) = \(\frac{1}{5}\)

ప్రశ్న17.
x = 2 sec θ; y = 2 tan θ అయిన x² – y² = 4 అని చూపుము.
జవాబు :
x² – y² = (2 sec θ)² – (2 tan θ)²
= 4 sec² θ – 4 tan² θ
= 4 (sec² θ – tan²θ)
= 4 (1) = 4

ప్రశ్న18.
√3 tan θ = 1 అయిన 9 విలువ ఎంత ?
జవాబు :
√3 tan θ = 1 = tan θ = \(\frac{1}{\sqrt{3}}\)
∴ θ = 30°.

ప్రశ్న19.
(sec 60°) (cos 60°) విలువ ఎంత ?
జవాబు :
(sec 60°) (cos 60°) = 1 (∵ sec θ – cos θ = 1)
(లేదా)
(sec 60°) (cos 60°) = 2 × ½ = 1.

ప్రశ్న20.
sin (60° + 30°) = ________
జవాబు :
sin (60° + 30°) = sin 90° = 1

ప్రశ్న21.
sec θ + tan θ = 3 అయిన sec θ – tan θ విలువ ఎంత ? ________
జవాబు :
sec θ + tan θ = ½
⇒ sec² θ – tan² θ = 1
⇒ (sec θ + tan θ) (sec θ – tan θ) = 1
⇒ \(\frac{1}{2}\) (sec θ – tan θ) = 1
∴ sec θ – tan θ = 1 × 2 = 2

ప్రశ్న22.
cot A = \(\frac{5}{12}\) అయిన sin A + cos A విలువను కనుగొనుము.
జవాబు :

cot A = \(\frac{5}{12}\)
AC = 13 (∵ 5, 12, 13 పైథాగరియన్ త్రికాలు)
∴ sin A + cos A = \(\frac{12}{13}+\frac{5}{13}=\frac{17}{13}\)

ప్రశ్న23.
ఈ క్రింది వాటిలో sin x కు సాధ్యం కాని విలువ ఏది?
A) \(\frac{3}{4}\)
B) \(\frac{3}{5}\)
C) \(\frac{4}{5}\)
D) \(\frac{5}{4}\)
జవాబు :
D) \(\frac{5}{4}\)

ప్రశ్న24.
sin θ = cos θ (0 < θ < 90) అయితే tan θ + cot θ విలువను కనుగొనుము.
జవాబు :
sin θ = cos θ
∴ θ = 45°. .
∴ tan θ + cot θ = tan 45 + cot 45
= 1 + 1 = 2
(లేదా)
sin θ = cos θ ⇒ \(\frac{\sin \theta}{\cos \theta}\) = 1
⇒ tan θ =1
∴ cot θ = 1
కొబట్టి tan θ + cot θ = 1 + 1 = 2

ప్రశ్న25.
sec θ + tan θ = 3 అయితే sec θ – tan θ = \(\frac{1}{3}\) అని చూపుము.
జవాబు :
sec θ + tan θ = 3
⇒ sec² θ – tan² θ = 1
⇒ (sec θ + tan θ) (sec θ – tan θ) = 1
⇒ 3 (sec θ – tan θ) = 1
∴ sec θ – tan θ = \(\frac{1}{3}\)

ప్రశ్న26.
∆ABC నందు AB = c, BC = a, AC = b మరియు ∠BAC = θ అయిన ∆ABC వైశాల్యము ……….. (θ అల్పకోణం )
A) \(\frac{1}{2}\) ab sin θ
B) \(\frac{1}{2}\) ca sin θ
C) \(\frac{1}{2}\) bc sin θ
D) \(\frac{1}{2}\) b² sin θ
జవాబు :
C) \(\frac{1}{2}\) bc sin θ

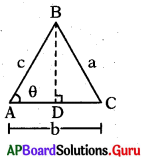
∆ADB లో ∠D = 90°
sin θ = \(\frac{\mathrm{BD}}{\mathrm{AB}}\)
⇒ BD = AB sin θ
= c sin θ

∆ABC వైశాల్యం. = \(\frac{1}{2}\) × భూమి × ఎత్తు
= \(\frac{1}{2}\) × AC × BD
= \(\frac{1}{2}\) bc sin a

ప్రశ్న27.
tan θ యొక్క విలువ cosec θ పదంలలో తెల్పండి.
జవాబు :
tan θ = \(\frac{1}{\cot \theta}=\frac{1}{\sqrt{{cosec}^{2} \theta-1}}\)

ప్రశ్న28.
ఈ క్రింది వాటిని పరిశీలించండి :
i) sin² 20° + sin² 70° = 1
ii) log₂ (sin 90°) = 1
క్రింది వానిలో సరియైనది ఏది ?
A) i) మాత్రమే
B) ii) మాత్రమే
C) i) మరియు ii) లు
D) i) మరియు ii) లు కావు
జవాబు :
A) i) మాత్రమే

ప్రశ్న29.
క్రింది ఏ విలువను నిర్వచించలేము ?
A) sin 90°
B) cos 0°
C) sec 90°
D) cos 90°
జవాబు :
C) sec 90°

ప్రశ్న30.
\(\sqrt{\frac{1-\cos ^{2} \theta}{1+\cot ^{2} \theta}}\) = sin² θ అని చూపుము
జవాబు :
\(\sqrt{\frac{1-\cos ^{2} \theta}{1+\cot ^{2} \theta}}=\sqrt{\frac{\sin ^{2} \theta}{{cosec}^{2} \theta}}=\frac{\sin \theta}{{cosec} \theta}\)
= sin θ · sin θ = sin² θ.

ప్రశ్న31.
tan 36°. tan 54° + sin 30° విలువ ఎంత ?
జవాబు :
tan 36°. tan 54° + sin 30°
= tan 36°. tan (90° – 36°) + \(\frac{1}{2}\)
= tan 36°. cot 36° + \(\frac{1}{2}\) = 1 + \(\frac{1}{2}\) = \(\frac{3}{2}\)

ప్రశ్న32.
sin A = \(\frac{24}{25}\) అయిన sec Aను కనుగొనుము
జవాబు :

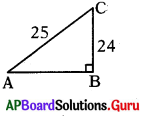
sin A = \(\frac{24}{25}\)
AC² = AB² + BC²
(25)² = AB² + (24)²
25² – 24² = AB²
(25 + 24) (25 – 24) = AB²
49(1) = AB²
AB = \(\sqrt{49}\) = 7

ప్రశ్న33.
4 cos² θ – 3 = 0 అయిన sin θ = \(\frac{1}{2}\) … అని చూపుము
జవాబు :
4 cos² θ – 3 = 0
⇒4 cos² θ = 3
⇒ cos² θ = \(\frac{3}{4}\) = cos θ = \(\sqrt{\frac{3}{4}}=\frac{\sqrt{3}}{2}\)
∴ θ = 30°
∴ sin θ = sin 30° = \(\frac{1}{2}\)
(లేదా)
4 cos² θ – 3 = 0
cos² θ = \(\frac{3}{4}\)
sin² θ = 1 – cos² θ = 1 – \(\frac{3}{4}\)
sin² θ = \(\frac{4-3}{4}=\frac{1}{4}\)
:: sin θ = \(\sqrt{\frac{1}{4}}=\frac{1}{2}\)

ప్రశ్న34.
cosec θ + cot θ = 2 అయిన cos θ ను కనుగొనుము
జవాబు :

ప్రశ్న35.
cos (A + B) = 0 మరియు cos B = \(\frac{\sqrt{3}}{2}\) అయిన ‘A’ కోణమును కనుగొనుము
జవాబు :
cos (A + B) = 0 ⇒ A + B = 90°
cos B = \(\frac{\sqrt{3}}{2}\) = B = 30°
⇒ A + B = 90° ⇒ A + 30° = 90°
∴ A= 60°

ప్రశ్న36.
sin x = \(\frac{5}{7}\) అయిన cosec x ను కనుగొనుము.
జవాబు :
sin x = \(\frac{5}{7}\) అయితే cosec x = \(\frac{7}{5}\)

ప్రశ్న37.
∠A = 75°, ∠B = 30°, అయిన tan (A – B) = 1 అని చూపుము.
జవాబు :
tan (A – B) = tan (75° – 30°)
= tan 45° = 1 .

ప్రశ్న38.
sec θ + tan θ = \(\frac{1}{3}\) అయిన sec θ – tan θ విలువ ఎంత ?
జవాబు :
sec θ + tan θ = \(\frac{1}{3}\)
⇒ sec² θ – tan² θ = 1
⇒ (sec θ + tan θ) (sec θ – tan θ) = 1
⇒ \(\frac{1}{3}\) (sec θ – tan θ) = 1
⇒ (sec θ – tan θ) = 1 × 3
∴ sec θ – tan θ = 3

ప్రశ్న39.
ఒక గడియారంలో 20 నిమిషాల వ్యవధిలో నిమిషాల ముల్లు చేయు కోణం ఎంత ?
జవాబు :
గడియారంలో 20 నిమిషాల వ్యవధిలో నిమిషాల ముల్లు చేయు కోణము = \(\frac{20}{60}\) × 360° = 120°

ప్రశ్న40.
sec θ – tan θ = 3 అయిన sec θ + tan θ విలువ ఎంత ?
జవాబు :
sec θ – tan θ = 3
⇒ sec²θ – tan²θ = 1
⇒ (sec θ + tan θ) (sec θ – tan θ) = 1
⇒ sec θ + tan θ (3) = 1
∴ sec θ + tan θ = \(\frac{1}{3}\)

ప్రశ్న41.
క్రింది పటములో BC విలువను కనుగొనుము.

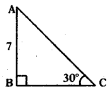
జవాబు :
tan 30° = AB
⇒ \(\frac{1}{\sqrt{3}}=\frac{7}{\mathrm{BC}}\) ⇒ BC = 7√3

ప్రశ్న42.
క్రింది పటం ∆ABC లో AB = ________ సెం.మీ.

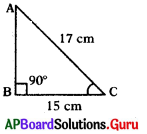
జవాబు :
AB² = AC² – BC²
= 17² – 15² = 289 – 225 = 64
∴ AB = \(\sqrt{64}\) = 8.

ప్రశ్న43.
sin 2θ = cos 3θ అయిన θ = 15° అని చూపుము.
జవాబు :
sin 2θ = cos 3θ
sin 2θ = sin (90 – 3θ)
⇒ 2θ = 90 – 3θ
⇒ 2θ + 3θ = 90°
⇒ 5θ = 90° ⇒ θ = \(\frac{90^{\circ}}{5}\) = 18°

ప్రశ్న44.
cos θ = \(\frac{3}{5}\) అయిన sin θ = ________
జవాబు :
cos θ = \(\frac{3}{5}\) అయిన sin θ = \(\frac{4}{5}\)
(∵3, 4, 5 పైథాగరియన్ త్రికాలు)

ప్రశ్న45.
cos 60° + sin 30° యొక్క విలువ ఎంత ?
జవాబు :
cos 60° + sin 30° = \(\frac{1}{2}+\frac{1}{2}\) = 1

ప్రశ్న46.
sec A + tan A = \(\frac{1}{5}\) అయిన sec A – tan A విలువ ఎంత ?
జవాబు :
5

ప్రశ్న47.
tan θ యొక్క వ్యుత్తమంను తెల్పండి.
జవాబు :
cot θ

ప్రశ్న48.
(sec²θ – 1) (cosec²θ – 1) = 1 అని చూపుము.
జవాబు :
(sec²θ – 1) (cosec² θ – 1) = 1 .
= tan²θ – cot²θ = 1

ప్రశ్న49.
sin (90 – A) = \(\frac{1}{2}\) అయితే A విలువ ఎంత ?
జవాబు :
(90 – A) = \(\frac{1}{2}\) ⇒ 90 – A = 30°
∴ 90° – 30° = A ⇒ A = 60°

ప్రశ్న50.
క్రింది వానిలో sin A = \(\frac{5}{13}\) నకు సరిపడు పటం

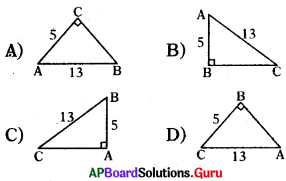
జవాబు :

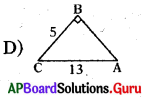
ప్రశ్న51.
sin² 60° – sin² 30° విలువ ఎంత ?
జవాబు :
sin² 60° – sin² 30° = \(\left(\frac{\sqrt{3}}{2}\right)^{2}-\left(\frac{1}{2}\right)^{2}\)
= \(\frac{3}{4}-\frac{1}{4}=\frac{2}{4}=\frac{1}{2}\)

ప్రశ్న52.
sin θ = \(\frac{a}{b}\), అయిన tan θ ను a, b లలో తెల్పండి.
జవాబు :
sin θ = \(\frac{a}{b}\)
∴ cos θ = \(\sqrt{1-\sin ^{2} \theta}\)

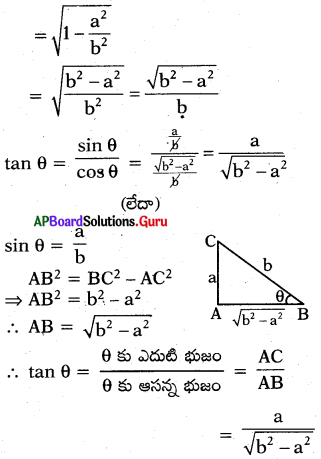
ప్రశ్న53.
cos² θ + sin² θ విలువ ఎంత ?
జవాబు :
1

ప్రశ్న54.
sin θ = cos θ అయిన 2 tan θ + cos² θ విలువను కనుగొనుము.
జవాబు :
sin θ = cos θ అయిన θ = 45°
∴ 2 tan θ + cos2 θ = 2 tan 45° + cos² 45°
= 2(1) + \(\left(\frac{1}{\sqrt{2}}\right)^{2}\)
= 2 + \(\frac{1}{2}=\frac{5}{2}\)

ప్రశ్న55.
cosec θ = 2 మరియు cot θ = √3p, ఇక్కడ θ లఘుకోణం అయిన ‘p’ విలువ ఎంత ?
జవాబు :
cosec θ = 2, cot θ = √3p
cosec² θ – cot² θ = 1.
= (2)² – (√3p)² = 1
= 4 – 3p² = 1
= -3p² = 1 – 4 = -3 .
∴ p² = \(\frac{-3}{-3}\) = 1
∴ p = √1 = ±1

ప్రశ్న56.
tan θ + sec θ = 8 అయిన sec θ – tan θ విలువ ఎంత ?
జవాబు :
sec θ – tan θ = \(\frac{1}{8}\)

ప్రశ్న57.
\(\left(\frac{11}{\cot ^{2} \theta}-\frac{11}{\cos ^{2} \theta}\right)\) విలువను కనుగొనుము.
జవాబు :
\(\frac{11}{\cot ^{2} \theta}-\frac{11}{\cos ^{2} \theta}\) = 11\(\left(\frac{1}{\cot ^{2} \theta}-\frac{1}{\cos ^{2} \theta}\right)\)
= 11 [tan²θ – sec² θ]
=-11 [sec² θ – tan²θ]
= -11 (1) = -11

ప్రశ్న58.
sec 2A = cosec (A – 27°) అయిన ∠A విలువ (2A లఘకోణము) ఎంత ?
జవాబు :
sec 2A = cosec (A – 27°)
cosec (90 – 2A) = cosec (A – 27°)
∴ 90 – 2A = A – 27
⇒ 90 + 27 = A + 2A
⇒ 3A = 117 = A = \(\frac{117}{3}\) = 39°

ప్రశ్న59.
\(\frac{1-\sec ^{2} A}{{cosec}^{2} A-1}\) = – tan⁴ A అని చూపుము.
జవాబు :
L.H.S. = \(\frac{1-\sec ^{2} A}{{cosec}^{2} A-1}\)
= \(\frac{-\left(\sec ^{2} A-1\right)}{{cosec}^{2} A-1}=\frac{-\tan ^{2} A}{\cot ^{2} A}\)
= – tan² A X tan² A
= – tan⁴ A = R.H.S.

ప్రశ్న60.
sin θ యొక్క గరిష్ట విలువ ఎంత ?
జవాబు :
sin θ యొక్క గరిష్ట విలువ ఎంత = 1

ప్రశ్న61.
tan θ = \(\frac{7}{8}\) అయిన \(\frac{(1+\sin \theta)(1-\sin \theta)}{(1+\cos \theta)(1-\cos \theta)}\)
జవాబు :

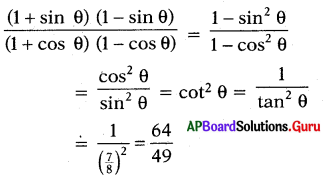
ప్రశ్న62.
క్రింది వానిలో ఏది త్రికోణమితీయ సర్వ సమీకరణము కాదు?
A) sin² 0 + cos² 0 = 1
B) sec² 0 – tan² 0 = 1
C) sec² 0 + cosec² 0 = 1
D) cosec² 0 – cot² 0 = 1
జవాబు :
C) sec² 0 + cosec² 0 = 1

ప్రశ్న63.
sec θ = 3k మరియు tan θ = \(\frac{3}{k}\) అయిన \(\left(\mathbf{k}^{2}-\frac{1}{\mathbf{k}^{2}}\right)=\frac{1}{9}\) అని చూపుము.
జవాబు :
sec θ = 3k, tan θ = \(\frac{3}{k}\)
sec² θ – tan² θ = 1
⇒ (31)² – \(\left(\frac{3}{\mathrm{k}}\right)^{2}\) = 1
⇒ 9\(\left(\mathrm{k}^{2}-\frac{1}{\mathrm{k}^{2}}\right)\) = 1 ⇒ k – \(\frac{1}{\mathrm{k}^{2}}=\frac{1}{9}\)

ప్రశ్న64.
క్రింది వానిని జతపరచడంలో సరైన సమాధానాన్ని

i) sin 90°	a) 0
ii) cosec 45°	b) 1
iii)tan 0°	c) √2
iv)cot 30°	d ) √3

A) i-b, ii-c, iii-a, iv-d
B) i-b, ii-a, iii-d, iv-c
C) i-a, ii-c, iii-b, iv-d
D) i-a, ii-b, iii-c, iv-d
జవాబు :
A) i-b, ii-c, iii-a, iv-d

ప్రశ్న65.
APQR యొక్క అంతరకోణాలు P, Q మరియు. R అయిన tan \(\)
A) sin \(\left(\frac{\mathrm{R}}{2}\right)\)
B) cot R
C) cot \(\left(\frac{\mathrm{R}}{2}\right)\)
D) tan \(\left(\frac{\mathrm{R}}{2}\right)\)
జవాబు :
C) cot \(\left(\frac{\mathrm{R}}{2}\right)\)

ప్రశ్న66.
\(\frac{2 \tan 30^{\circ}}{1+\tan ^{2} 30^{\circ}}\) విలువ
A) sin 60°
B) cos 30°
C) tan 60°
D) A మరియు B
జవాబు :
D) A మరియు B

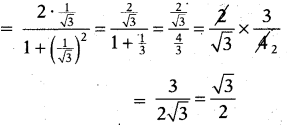
∴ sin 60° మరియు cos 30°

ప్రశ్న67.
sin (x – 20)° = cos (3x – 10)° అయిన ‘x’ విలువను కనుగొనుము.
జవాబు :
sin (x – 20)° = cos (3x – 10)
[∵ sin A = cos B అయితే A + B = 90]
∴ x – 20 + 3x – 10 = 90
⇒ 4x = 90° + 30° = 120°
⇒ x = \(\frac{120^{\circ}}{4}\) = 30°

ప్రశ్న68.
\(\frac{1}{\sec \theta}\) 0 ≤ θ ≤ 90° యొక్క గరిష్ఠ విలువ ఎంత ?
జవాబు :
2

ప్రశ్న69.
cos² 17° – sin² 73° యొక్క విలువను కనుగొనుము.
జవాబు :
cos² 17° – sin² 73°
= cos² (90° – 73°) – sin² 73°
= sin² 73° – sin² 73° = 0
(∵ cos (90 – θ) = sin θ)

ప్రశ్న70.
A = 30° అయిన sin 2A విలువ ఎంత ?
జవాబు :
A = 30° అయిన sin 2A = sin 60° = \(\frac{\sqrt{3}}{2}\)

ప్రశ్న71.
sin 45° + cos45° యొక్క విలువ √2 చూపుము.
జవాబు :

ప్రశ్న72.
లంబకోణ త్రిభుజం ABC లో, లంబకోణం ‘C’ వద్ద కలదు. tan A = \(\frac{8}{15}\) అయిన cosec²A – 1 విలువ ఎంత ?
జవాబు :
tan A = \(\frac{8}{15}\) మరియు
cosec² – A – 1 = cot² A
= \(\frac{1}{\tan ^{2} A}=\frac{1}{\left(\frac{8}{15}\right)^{2}}=\frac{225}{64}\)

ప్రశ్న73.
\(\frac{1}{2}\)tan² 45° = sin² A మరియు ‘A’ లఘుకోణము అయిన A విలువ ఎంత ?
జవాబు :
\(\frac{1}{2}\)tan² 45° = sin² A
\(\frac{1}{2}\)(1)² = sin² A
⇒ \(\frac{1}{2}\) = sin² A ⇒ sin A = \(\frac{1}{\sqrt{2}}\)
∴ A = 45° (∵ sin45° = \(\frac{1}{\sqrt{2}}\))

ప్రశ్న74.
వాక్యం – I : ∆ABC లో ∠A, ∠B మరియు ∠C లు త్రిభుజ అంతర కోణాలైన sin \(\frac{A+B}{2}\) = cos\(\frac{C}{2}\)
వాక్యం – II : x = sin θ, y = cos θ అయిన x² + y² = 0.
A) I మాత్రమే సత్యం
B) II మాత్రమే సత్యం
C) మరియు II లు రెండూ అసత్యం
D) I మరియు II లు రెండూ సత్యం
జవాబు :
C) మరియు II లు రెండూ అసత్యం

ప్రశ్న75.
tan θ =1 అయిన \(\frac{5 \sin \theta+4 \cos \theta}{5 \sin \theta-4 \cos \theta}\) విలువను కనుగొనుము. (θ అల్పకోణము)
జవాబు :
tan θ = 1 ⇒ θ = 45° (∵ tan 45° = 1)

ప్రశ్న76.
cos 2θ = sin 4θ మరియు 2θ మరియు 4θ లు లఘుకోణాలైన ‘θ’ విలువ ఎంత ?
జవాబు :
cos 2θ = sin 4θ
sin (90 – 2θ) = sin 4θ
∴ 90 – 2θ = 4θ ⇒ 90 = 4θ + 2θ = 6θ
∴ θ = \(\frac{90^{\circ}}{6}\) = 15° ∴ θ = 15°
(లేదా)
2θ + 4θ = 90° (∵ sin A = cos B ⇒ A + B = 90°)
6θ = 90° ⇒ θ = \(\frac{90^{\circ}}{6}\) = 15°

ప్రశ్న77.
θ విలువ క్రింది వానిలో ఏది అయినప్పుడు tan θ విలువని నిర్వచించలేము ?
A) 90°
B) 60°
C) 30°
D) 0°
జవాబు :
A) 90°

ప్రశ్న78.
sin x = cos x, 0 ≤ x ≤ 90° అయిన x విలువ ఎంత ?
జవాబు :
x = 45°

ప్రశ్న79.
క్రింది వానిలో tanA = \(\frac{5}{12}\) ను ప్రాతినిధ్యపరుచుటకు సరైన పటము.

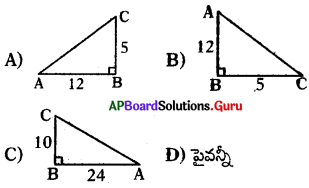
జవాబు :
D) పైవన్నీ

ప్రశ్న80.
sin45° – cos 45° + cos 60° = tan θ అయిన θ విలువను కనుగొనుము.
జవాబు :
sin 45° . cos 45° + cos 60° = tan θ
\(\frac{1}{\sqrt{2}} \times \frac{1}{\sqrt{2}}+\frac{1}{2}\) = tan θ
\(\frac{1}{2}+\frac{1}{2}\) = tan θ ⇒ tan θ = 1
∴ θ = 45°

→ క్రింది పటం నుండి ON = x; PN = y; OP = r; ∠PON = θ మరియు ∠PNO = 90° అయిన 81 మరియు 82 ప్రశ్నలకు సమాధానాలు రాయండి.

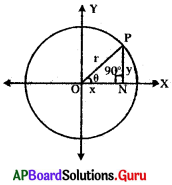
ప్రశ్న81.
cos θ ను x, r’ లలో తెల్పండి.
జవాబు :
cos θ = \(\frac{\mathbf{x}}{\mathbf{r}}\)

ప్రశ్న82.
tan θ ను x, y లలో తెల్పండి.
జవాబు :
tan θ = \(\frac{\mathbf{y}}{\mathbf{r}}\)

ప్రశ్న83.
sin θ cosec θ + cos θ . sec θ + tan θ. cot θ = 3 అని చూపుము
జవాబు :
sin θ cosec θ + cos θ . sec θ + tan θ. cot θ

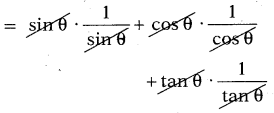
= 1 + 1 + 1 = 3

ప్రశ్న84.
sin θ. cosec θ = x అయిన x విలువ ఎంత ?
జవాబు :
sin θ. cosec θ = x

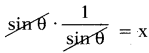
∴ x = 1

ప్రశ్న85.
sin θ = \(\frac{a}{b}\) అయిన cos θను a, b లలో తెల్పండి
జవాబు :

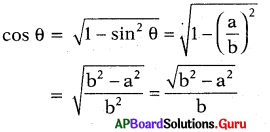
ప్రశ్న86.
sin θ = 12 అయిన tan θ విలువ ఎంత ?
జవాబు :

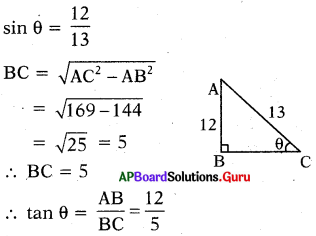
ప్రశ్న87.
sin θ. sec θ = tan θ అని చూపుము.
జవాబు :
L.H.S. = sin θ. sec θ
= sin 8 . \(\frac{1}{\cos \theta}\)
= \(\frac{\sin \theta}{\cos \theta}\) = tan θ = R.H.S.

ప్రశ్న88.
\(\sqrt{1+\cot ^{2} \theta}\) = cosec θ అని నిరూపించుము.
జవాబు :
\(\sqrt{1+\cot ^{2} \theta}=\sqrt{{cosec}^{2} \theta}\) = cosec θ

ప్రశ్న89.
sec θ = \(\frac{13}{12}\) అయిన sin θ విలువ ఎంత ?
జవాబు :

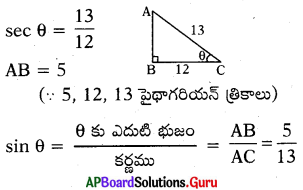
ప్రశ్న90.
జతపరుచుము.

A) i-c, ii-a, iii-d, iv-b
B) i-b, ii-d, iii-a, iv-c
C) i-a, ii-d, iii-c, iv-b
D) i-d, ii-b, iii-a, iv-c
జవాబు :
B) i-b, ii-d, iii-a, iv-c

ప్రశ్న91.
\(\sqrt{1+\sin A} \cdot \sqrt{1-\sin A}\) = cos A అని చూపుము.
జవాబు :

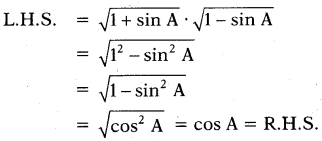
ప్రశ్న92.
ప్రవచనం – A: sin 0°, sin 30°, sin 90° యొక్క విలువలు అంకశ్రేణిలో కలవు.
ప్రవచనం – B: tan 45°, sec 60°, cosec-30° యొక్క విలువలు ఒక గుణశ్రేణిని ఏర్పరుస్తాయి.
A) A సత్యం, B అసత్యం
B) A అసత్యం, B సత్యం
C) A సత్యం, B సత్యం
D) A అసత్యం, B అసత్యం
జవాబు :
C) A సత్యం, B సత్యం

ప్రశ్న93.
tan² 30° + 2cot² 60° విలువ ఎంత ?
జవాబు :
tan² 30° + 2cot² 60°
= \(\left(\frac{1}{\sqrt{3}}\right)^{2}+2\left(\frac{1}{\sqrt{3}}\right)^{2}\)
= \(\frac{1}{3}+2 \cdot \frac{1}{3}=\frac{1}{3}+\frac{2}{3}=\frac{3}{3}\) = 1

ప్రశ్న94.
sin² 75° + cos² 75° విలువ ఎంత ?
జవాబు :
1.
(sin² θ + cos² θ = 1)

ప్రశ్న95.
sin⁴ θ – cos⁴ θ =
A) 1
B) cos² θ – sin² θ
C) 2 sin² θ – 1
D) 2 sin² θ
జవాబు :
C) 2 sin² θ – 1

sin⁴ θ – cos⁴ θ = (sin² θ + cos² θ) (sin² θ – cos² θ)
= 1 (sin² θ – cos² θ)
= sin² θ – cos² θ
= sin² θ – (1 – sin² θ)
= sin² θ – 1 + sin² θ
= 2 sin² θ – 1

ప్రశ్న96.
tan θ = \(\frac{1}{\sqrt{3}}\); అయిన cos θ విలువ ఎంత ? (θ అల్పకొణము)
జవాబు :
tan θ = \(\frac{1}{\sqrt{3}}\) ⇒ θ = 30°
∴ cos θ = cos 30° = \(\frac{\sqrt{3}}{2}\)

ప్రశ్న97.
(1 + tan θ)² = sec² θ + 2 tan θ అని చూపుము
జవాబు :
L.H.S. = (1 + tanθ)²
= 1² + tan² θ + 2(1) tan θ
(: (a + b)² = a² + b² + 2ab)
= 1 + tan² θ + 2 tan θ
= sec² θ + 2 tan θ = R.H.S.
L.H.S. = R.H.S.

ప్రశ్న98.
tan θ ను sec θ లలో తెలుపగా
A) \(\frac{\sqrt{\sec ^{2} \theta-1}}{\sec \theta}\)
B) \(\frac{\sec \theta}{\sqrt{\sec ^{2} \theta-1}}\)
C) \(\frac{1}{\sqrt{\sec ^{2} \theta-1}}\)
D) \(\sqrt{\sec ^{2} \theta-1}\)
జవాబు :
D) \(\sqrt{\sec ^{2} \theta-1}\)

sec² θ – tan² θ = 1
sec² A – 1= tan² θ
tan θ = \(\sqrt{\sec ^{2} \theta-1}\)

ప్రశ్న99.
5 sin A = 3 అయిన sec² A – tan² A విలువ ఎంత ?
జవాబు :
5 sin A = 3 అయిన sec² A – tan² A = 1
(∵ sec² A – tan² A = 1)

ప్రశ్న100.
tan θ ను sin θ లో తెల్పండి.
జవాబు :
tan θ = \(\frac{\sin \theta}{\cos \theta}=\frac{\sin \theta}{\sqrt{1-\sin ^{2} \theta}}\)
(∵ sin² θ + cos² θ = 1
cos² θ = 1 – sin² θ
cos θ = \(\sqrt{1-\sin ^{2} \theta}\))

ప్రశ్న101.
cos θ = \(\frac{\sqrt{3}}{2}\) మరియు 8 అల్పకోణము అయిన 4 sin² θ + tan² θ విలువ ఎంత ?
జవాబు :
cos θ = \(\frac{\sqrt{3}}{2}\)
∴ θ = 30°
∴ 4 sin² θ + tan² θ
= 4 sin² 30° + tan² 30°
= 4\(\left(\frac{1}{2}\right)^{2}\) + \(\left(\frac{1}{\sqrt{3}}\right)^{2}\) = 1 + \(\frac{1}{3}=\frac{4}{3}\)

ప్రశ్న102.

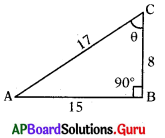
పటం నుండి, ∆ABC లో ∠B = 90°; ∠C = θ అయిన tan θ విలువను రాయండి.
జవాబు :
tan θ = \(\frac{\mathrm{AB}}{\mathrm{BC}}=\frac{15}{8}\)

ప్రశ్న103.

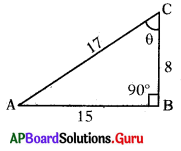
‘పటం నుండి cos θ విలువను తెల్పండి.
జవాబు :
cos θ = \(\frac{\mathrm{BC}}{\mathrm{AC}}=\frac{8}{17}\)

ప్రశ్న104.
cos 0° + sin 90° + √2 sin 45° = 3 అని చూపండి.
జవాబు :
cos 0° + sin 90° + √2 sin 45°
= 1 + 1 + √2 × \(\frac{1}{\sqrt{2}}\) = 1 + 1 + 1 = 3

ప్రశ్న105.
3 sin² 45° + 2 cos² 60° విలువ ఎంత ?
జవాబు :
3 sin² 45° + 2 cos² 60°
= 3\(\left(\frac{1}{\sqrt{2}}\right)^{2}\) + 2\(\left(\frac{1}{2}\right)^{2}\)
= \(\frac{3}{2}+2 \times \frac{1}{4}=\frac{3}{2}+\frac{1}{2}\) = 2

ప్రశ్న106.
sin (log₂ 1)° విలువ ఎంత ?
జవాబు :
sin (log₂ 1)° = sin 0° = 0 (∵ log 1 = 0)

ప్రశ్న107.
a⁴ – b⁴ = (a² + b²) (a² – b²) అనే సూత్రాన్ని ఉపయోగించి sin⁴ θ – cos⁴ θ ను సూక్ష్మీకరించగా వచ్చు ఫలితం క్రింది వానిలో దేనికి సమానం ?
A) sin²θ – cos²θ
B) 2 sin²θ – 1
C) 1 – 2cos²θ
D) పైవన్నీ
జవాబు :
D) పైవన్నీ

sin⁴θ – cos⁴θ
= (sin² θ + cos² θ) (sin² θ – cos² θ)
= sin² θ – cos² θ …….. (1)
= sinθ – (1 – sin²θ)
= sin²θ – 1 + sin²θ
= 2 sin²θ – 1 …….. (2)
(1) ⇒ (1 – cos² θ) – cos²θ = 1 – 2cos²θ

ప్రశ్న108.
tan θ + cot θ = 2 అయిన tan θ + cot θ విలువ ఎంత?
జవాబు :
tan θ + cot θ = 2
(tan θ + cot θ)² = (2)²

= tan² θ + cot² θ + 2 = 4
= tan² θ + cot² θ = 4 – 2 = 2

ప్రశ్న109.
క్రింది పట్టికలో లోపించిన విలువను తెల్పండి.

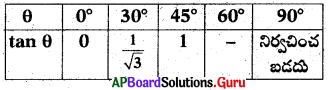
జవాబు :
√3

ప్రశ్న110.
∆ABC లో sin A = \(\frac{3}{5}\), cos A = \(\frac{4}{5}\) అయిన ఆ త్రిభుజ కొలతలు వరుసగా BC, AB, AC లు క్రింది వానిలో ఏవి కావచ్చును ?
(A) 9, 12, 15
(B) 3, 4, 5,
(C) 12, 16, 20
(D) పైవన్నీ
జవాబు:
D) పైవన్నీ

ప్రశ్న111.
(1 + tan² 60°)² విలువను కనుగొనుము.
జవాబు :
(1 + tan²60°)² = (1 + (√3)²)²
= 4² = 16

ప్రశ్న112.
క్రింది వానిని జతపరుచుము.

i) sec θ	a) \(\frac{1}{\sin \theta}\)
ii) cosec θ	b) \(\frac{1}{\tan \theta}\)
iii)cot θ	c) \(\frac{1}{\cos \theta}\)

A) i-a, ii-b, iii-c
B) i-c, ii-a, iii-b
C) i-b, ii-a, iii-c,
D) i-a, ii-c, iii-b
జవాబు :
B) i-c, ii-a, iii-b

→ ఇవ్వబడిన పటాన్ని పరిశీలించి, 113, 114 ప్రశ్నలకు జవాబులు రాయండి.

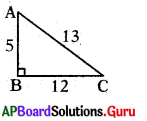
ప్రశ్న113.
sin A విలువను తెల్పండి.
జవాబు :
sin A = \(\frac{12}{13}\)

ప్రశ్న114.
tan C విలువను రాయండి.
జవాబు :
tan C = \(\frac{5}{12}\)

ప్రశ్న115.
α + β = 90° మరియు α = 2β అయిన cos² α + sin² β = \(\frac{1}{2}\) అని చూపుము.
జవాబు :
α + β = 90°, α = 2β
2β + β = 90° ⇒ 3β = 90° ⇒ β = 30°
∴ α = 60°
cos² α + sin² β = cos² 60° + sin² 30°
= \(\left(\frac{1}{2}\right)^{2}+\left(\frac{1}{2}\right)^{2}=\frac{1}{4}+\frac{1}{4}=\frac{2}{4}=\frac{1}{2}\)

ప్రశ్న116.
∆ABC లంబకోణ త్రిభుజంలో ∠B = 90°, BC = 24 సెం.మీ. మరియు tan C = \(\frac{5}{12}\) అయిన కర్ణము AC పొడవు ఎంత ?
జవాబు :

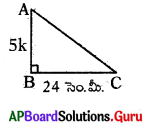
BC = 24 సెం.మీ. మరియు
tan C = \(\frac{\mathrm{AB}}{\mathrm{BC}}=\frac{5}{12}\)
\(\frac{5}{12}=\frac{5 \mathrm{k}}{24}\) ⇒ k= 2
AB = 10 సెం.మీ.
కర్ణం AC = \(\sqrt{\mathrm{AB}^{2}+\mathrm{BC}^{2}}=\sqrt{10^{2}+24^{2}}\)
= \(\sqrt{100+576}=\sqrt{676}\) = 26 సెం.మీ.
(లేదా)
tan C = \(\frac{5}{12}\) (5, 12, 13 లు పైథాగరియన్ త్రికాలు),
BC = 24 సెం.మీ. (10, 24, 26 లు కూడా పైథాగరియన్ త్రికాలు)
∴ కర్ణం AC = 26 సెం.మీ.

ప్రశ్న 117.
క్రింది వానిని జతపరచడంలో సరైన సమాధానమును ఎన్నుకొనుము.

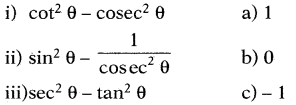
(A) i-a, ii-b, iii-c
(B) i-b, ii-c, iii-a
(C) i-c, ii-b, iii-a
(D) i-c, ii-a, iii-b
జవాబు.
(C) i-c, ii-b, iii-a

ప్రశ్న 118.
ప్రవచనం P: sin α = cos β అయిన α + β = 90° (α, β లు అల్పకోణాలు)
ప్రవచనం – Q : sec θ = m, tan θ = n అయిన m² – 12 = 1 (0° < θ < 90°)
(A) P సత్యం, Q అసత్యం
(B) P సత్యం, Q సత్యం
(C) P అసత్యం, Q సత్యం
(D) P అసత్యం , Q అసత్యం .
జవాబు.
(B) P సత్యం, Q సత్యం

ప్రశ్న 119.
sin 60° విలువ
(A) cos 30°
(B) \(\frac{\sqrt{3}}{2}\)
(C) A మరియు B
(D) \(\frac{1}{2}\)
జవాబు.
(C) A మరియు B

ప్రశ్న 120.
A, B లు లఘుకోణాలైన sin (A – B) = \(\frac{1}{2}\) sin A = \(\frac{1}{2}\) అయిన B ని కనుగొనుము.
సాధన.
sin (A – B) = \(\frac{1}{2}\) ⇒ A – B = 30°
sin A = \(\frac{1}{2}\) ⇒ A = 30°
∴ 30° – B = 30° ⇒ B = 0°
(లేదా)
sin (A – B) = sin A = \(\frac{1}{2}\)
∴ A – B = A ⇒ – B = A – A ⇒ B = 0

ప్రశ్న 121.
∆ ABC లో a = 3; b = 4; c=’5 అయిన cos A విలువను కనుగొనుము.
సాధన.

cos A = \(\frac{\mathrm{AC}}{\mathrm{AB}}\) = \(\frac{4}{5}\)

ప్రశ్న 122.
sec A . \(\sqrt{1-\sin ^{2} A}\) = 1 అని చూపుము.
సాధన.

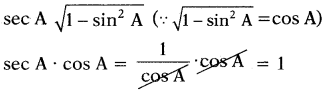
ప్రశ్న 123.
sec²35° – co²55° = 1 అని నిరూపించండి.
సాధన.
sec²35° – cot² (90 – 35) (∵ cot (90 – θ) = tan θ)
sec²35° – tan²35° = 1

ప్రశ్న 124.
\(\frac{\sin 18^{\circ}}{\cos 72^{\circ}}\) విలువ ఎంత ?
సాధన.
\(\frac{\sin 18^{\circ}}{\cos 72^{\circ}}\) = \(\frac{\sin (90-72)}{\cos 72^{\circ}}\) = \(\frac{\cos 72^{\circ}}{\cos 72^{\circ}}\) = 1

ప్రశ్న 125.
cos 1° ∙ cos 2° ∙ cos 3°…….. cos 90° విలువ ఎంత ?
సాధన.
cos 1° – cos 2° – cos 3° …….. cos 90° = 0 (∵ cos 90° = 0)

ప్రశ్న 126.
cot θ = p, sec θ = q అయిన క్రింది వానిలో ఏది సత్యం ?
(A) p² – q² = 1
(B) q² – p² = 1
(C) q² – \(\frac{1}{\mathrm{p}^{2}}\) = 1
(D) \(\frac{1}{\mathrm{q}^{2}}\) – p² = 1
సాధన.
C.
cot θ = p ⇒ tan θ = \(\frac{1}{\mathrm{p}}\)
sec² θ – tan² θ = q² – \(\left(\frac{1}{p}\right)^{2}\) = q² – \(\frac{1}{\mathrm{p}}\)

ప్రశ్న 127.
ఒక లంబకోణ త్రిభుజ భుజాలు పూర్ణాంకాలు మరియు tan θ = \(\frac{5}{12}\), అయితే ఆ త్రిభుజము యొక్క కనిష్ఠ వైశాల్యము ఎంత ?
సాధన.

త్రిభుజము యొక్క కనిష్ట వైశాల్యము = \(\frac{1}{2}\)ab
= \(\frac{1}{2}\) × 5 × 12 = 30 చ.సెం.మీ.

ప్రశ్న 128.
\(\frac{\sqrt{1+\tan ^{2} \theta}}{\sqrt{1+\cot ^{2} \theta}}\) = tan θ అని చూపుము
సాధన.

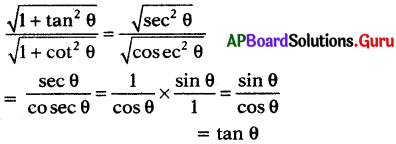
ప్రశ్న 129.
sin² 47° + sin² 43° విలువ ఎంత ?
సాధన.
sin² 47° + sin² 43° .
= sin² 47° + sin² (90 – 47)°
= sin² 47° + cos² 47° = 1

ప్రశ్న 130.
cos \(\left(\frac{\theta}{2}\right)\) = \(\frac{1}{\sqrt{2}}\) అయిన cos θ విలువ ఎంత ?
సాధన.
cos \(\left(\frac{\theta}{2}\right)\) = \(\frac{1}{\sqrt{2}}\) ⇒ \(\frac{\theta}{2}\) = 45° ⇒ θ = 90°
∴ cos θ = cos 90° = 0

ప్రశ్న 131.
sin θ = \(\frac{\sqrt{3}}{2}\) అయిన sin \(\left(\frac{\theta}{2}\right)\) విలువ ఎంత ?
సాధన.
sin θ = \(\frac{\sqrt{3}}{2}\) ⇒ θ = 60° ∴ \(\frac{\theta}{2}\) = 30°
sin \(\frac{\theta}{2}\) = sin 30° = \(\frac{1}{2}\)

ప్రశ్న 132.
(1 + cot² 45°)² విలువ ఎంత ?
సాధన.
(1 + cot² 45°)² = (1 + 1²)²
= (1 + 1)² = 2² = 4

ప్రశ్న 133.
\(\frac{1-\tan ^{2} 30^{\circ}}{1+\tan ^{2} 30^{\circ}}\) విలువ ఎంత ?
సాధన.

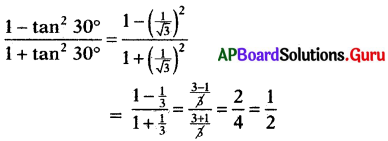
ప్రశ్న 134.
\(\frac{{cosec}^{2} \theta}{\cot \theta}\) – cot θ = tan θ అని చూపుము.
సాధన.

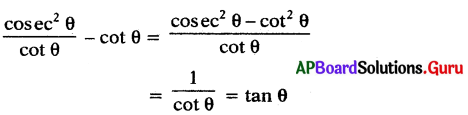
ప్రశ్న 135.
\(\sqrt{\frac{\sec x+\tan x}{\sec x-\tan x}}\) =
(A) sec x + tan x
(B) sec x – tan x
(C) 2 tan x
(D) 2 sec x
సాధన.
(A) sec x + tan x

ప్రశ్న 136.
4 sin 30° ∙ sec 60° = x tan 45° అయిన విలువ ఎంత?
సాధన.
4 sin 30° ∙ sec 60° = x tan 45°
⇒ 4 × \(\left(\frac{1}{2}\right)\)(2) = x(1) ⇒ 4 = x
∴ x = 4

ప్రశ్న 137.
sin 60° cos 30° + cos 60°. sin 30° విలువ ఎంత?
సాధన.
sin 60° . cos 30° + cos 60°. sin 30°
= \(\left(\frac{\sqrt{3}}{2}\right)\left(\frac{\sqrt{3}}{2}\right)+\left(\frac{1}{2}\right)\left(\frac{1}{2}\right)\)
= \(\frac{3}{4}+\frac{1}{4}=\frac{4}{4}\) = 1
(లేదా)
sin 60° · cos 30° + cos 60°. sin 30°
= sin (60° + 30°) = sin 90° = 1

ప్రశ్న 138.
sin (A + B) = \(\frac{\sqrt{3}}{2}\); cos B = \(\frac{\sqrt{3}}{2}\) అయిన A విలువను కనుగొనుము.
సాధన.
sin (A + B) = \(\frac{\sqrt{3}}{2}\), cos B = \(\frac{\sqrt{3}}{2}\)
A + B = 60°, B = 30°
A + 30° = 60° ⇒ A = 30°

ప్రశ్న 139.
\(\frac{\tan 45^{\circ}}{{cosec} 30^{\circ}}+\frac{\sec 60^{\circ}}{\cot 45^{\circ}}\) =
(A) 2\(\frac{1}{2}\)
(B) \(\frac{5}{2}\)
(C) 2
(D) A మరియు B
సాధన.
(D) A మరియు B
\(\frac{\tan 45^{\circ}}{{cosec} 30^{\circ}}+\frac{\sec 60^{\circ}}{\cot 45^{\circ}}\) = \(\frac{1}{2}+\frac{2}{1}\) = 2\(\frac{1}{2}\) = \(\frac{5}{2}\)

ప్రశ్న 140.
cos (A – B) = \(\frac{1}{2}\); sin B = \(\frac{1}{\sqrt{2}}\) అయిన A విలువను కనుగొనుము.
సాధన.
COS (A – B) = \(\frac{1}{2}\), sin B = \(\frac{1}{\sqrt{2}}\)
A – B = 60°,
B = 45°
∴ A = 60° + B = 60° + 45° = 105°

ప్రశ్న 141.
cos 75° విలువ క్రింది వానిలో దేనికి సమానము ?
(A) sin 15°
(B) – sin 15°
(C) cos 15°
(D) \(\frac{\sqrt{3}}{2}\)
సాధన.
(A) sin 15°
cos 75° = cos (90 – 15)° = sin 15.

ప్రశ్న 142.
(1 + tan² A) (1 – sin² A) = 1 అని చూపండి.
సాధన.
(1 + tan² A) (1 – sin² A)
= sec² A – cos² A

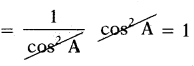
ప్రశ్న 143.
tan 30° =
(A) √3
(B) cot 60°
(C) \($\frac{1}{\sqrt{3}}$\)
(D) B మరియు C .
జవాబు.
(D) B మరియు C .

ప్రశ్న 144.
sin²45° + cos²45° + tan²45° = 2 అని నిరూపించుము.
సాధన.
sin²45° + cos²45° + tan²45°
= 1 + 1 = 2 [∵ sin²θ + cos² θ = 1]

ప్రశ్న 145.
\(\frac{\sin ^{4} A-\cos ^{4} A}{\sin ^{2} A-\cos ^{2} A}\) = 1 అని చూపుము.
సాధన.

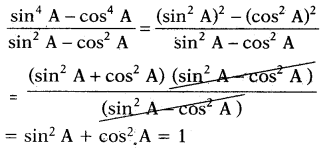
ప్రశ్న 146.
sin θ = \(\frac{1}{2}\) అయిన cos \(\frac{3 \theta}{2}\) విలువ ఎంత ?
సాధన.
sin θ = \(\frac{1}{2}\) ⇒ θ = 30°
cos \(\left(\frac{3 \theta}{2}\right)\) = cos\(\left(\frac{3(30)}{2}\right)\)
= cos 45° = \(\frac{1}{\sqrt{2}}\)

ప్రశ్న 147.
cos (90 – θ) =
(A) cos θ
(B) sin θ
(C) – sin θ
(D) sec θ
సాధన.
(B) sin θ

ప్రశ్న 148.
\(\frac{\tan \theta \cdot \sqrt{1-\sin ^{2} \theta}}{\sqrt{1-\cos ^{2} \theta}}\) = 1 అని నిరుపించుము
సాధన.

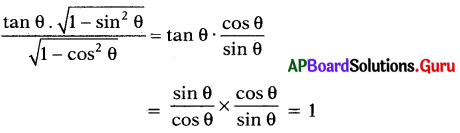
ప్రశ్న 149.
sec θ + tan θ = \(\frac{1}{5}\) అయిన sin θ విలువను కనుగోనుము.
సాధన.

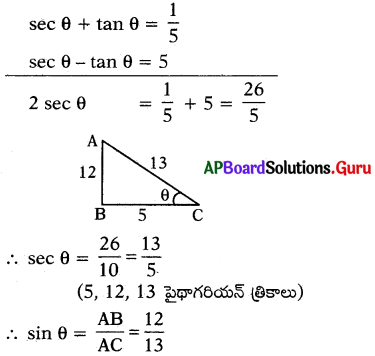
ప్రశ్న 150.
(sec 45° + tan 45°) (sec 45° – tan 45°) విలువ ఎంత?
సాధన.
(sec 45° + tan 45°) (sec 45° – tan 45°)
= (sec² 45° – tan² 45°)
= 1

ప్రశ్న 151.
sin 30° + cos 60° విలువ ఎంత?
సాధన.
sin 30° + cos 60° = \(\frac{1}{2}\) + \(\frac{1}{2}\) = 1

ప్రశ్న 152.
\(\sqrt{{cosec}^{2} \theta-\cot ^{2} \theta}\) విలువ ఎంత?
సాధన.
\(\sqrt{{cosec}^{2} \theta-\cot ^{2} \theta}\) = √1 = ± 1

ప్రశ్న 153.
tan A ను cos A లో రాయండి.
సాధన.
tan A = \(\frac{\sin A}{\cos A}=\frac{\sqrt{1-\cos ^{2} A}}{\cos A}\)

ప్రశ్న 154.
\(\frac{1}{1-\sin \theta}+\frac{1}{1+\sin \theta}\) = 2 sec² θ అని చూపుము
సాధన.

ప్రశ్న 155.
sec θ + tan θ = 4 అయిన cos θ విలువను కనుగొనుము.
సాధన.

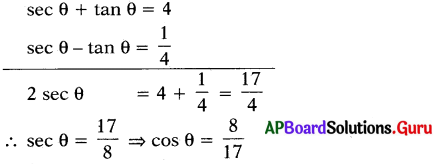
ప్రశ్న 156.
cot² θ = 3 అయిన cosec θ = i.
సాధన.
cot² θ = 3
cosec² θ – cot² θ = 1
⇒ cosec²θ – 3 = 1
⇒ cosec² θ = 1 + 3 = 4
⇒ cosec θ = 4 = 2
(లేదా)
cot² θ = 3 ⇒ cot θ = √3 ⇒ θ = 30°
∴ cosec θ = cosec 30° = 2

ప్రశ్న 157.
tan 0° విలువను రాయండి.
సాధన.
tan 0° = 0

ప్రశ్న 158.
cos θ = – cos θ అయిన θ విలువ ఎంత?
సాధన.
cos θ = – cos θ
⇒ cos θ + cos θ = 0
⇒ cos θ = \(\frac{0}{2}\) = 0
∴ θ = 90°

ప్రశ్న 159.
sin θ = \(\frac{a}{b}\); cos θ = \(\frac{c}{d}\) అయిన cot θ =
(A) \(\frac{\mathrm{ab}}{\mathrm{cd}}\)
(B) \(\frac{\mathrm{bc}}{\mathrm{ad}}\)
(C) \(\frac{c a}{b d}\)
(D) \(\frac{\mathrm{ad}}{\mathrm{bc}}\)
సాధన.
(B) \(\frac{\mathrm{bc}}{\mathrm{ad}}\)

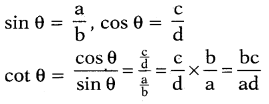
ప్రశ్న 160.
A అల్ప కోణ౦ మరియు tan A = \(\frac{1}{\sqrt{3}}\) అయిన sin A విలువ ఎంత ?
సాధన.
tan A = \(\frac{1}{\sqrt{3}}\) ⇒ A = 30°
∴ sin A = sin 30° = \(\frac{1}{2}\)

ప్రశ్న 161.
a sin θ = x; b cos θ = y అయిన \(\left(\frac{x}{a}\right)^{2}+\left(\frac{y}{b}\right)^{2}\) =
(A) – 1
(B) 0
(C) 2
(D) 1
సాధన.
(D) 1
a sin θ = x, b cos θ = y
sin θ = \(\frac{x}{a}\) cos θ = \(\frac{y}{b}\)
∴ \(\left(\frac{x}{a}\right)^{2}+\left(\frac{y}{b}\right)^{2}\) = sin² θ + cos² θ = 1

ప్రశ్న 162.
sin A = \(\frac{1}{\sqrt{2}}\) అయిన tan A విలువ ఎంత>
సాధన.
sin A = \(\frac{1}{\sqrt{2}}\) ⇒ A = 45°
∴ tan A = tan 45° = 1

ప్రశ్న 163.
cos (x – y) =
(A) cos x sin x + cos y sin y
(B) cos x sin y + cos y sin x
(C) sin x cos y + cos x sin y
(D) cos x cos y + sin x sin y
సాధన.
(D) cos x cos y + sin x sin y
cos (x – y) = cos x cos y + sin x sin y

ప్రశ్న 164.
sec θ = cosec θ అయిన θ విలువ =
(A) 90°
(B) 45°
(C) 30°
(D) 60°
సాధన.
(B) 45°

ప్రశ్న 165.
\(\frac{\sqrt{{cosec}^{2} \theta-1}}{{cosec} \theta}\) =
(A) 1 + sec θ
(B) cosec θ + cot θ
(C) cos θ
(D) tan θ
సాధన.
(C) cos θ

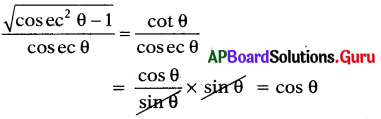
ప్రశ్న 166.
\(\frac{\sin \theta}{\sqrt{1-\sin ^{2} \theta}}\) = tan θ అని చూపుము.
సాధన.
\(\frac{\sin \theta}{\sqrt{1-\sin ^{2} \theta}}\) = \(\frac{\sin \theta}{\cos \theta}\) = tan θ

ప్రశ్న 167.
cos A = sin B అయిన A + B = 90° అని చూపుము.
సాధన.
cos A = sin B
sin (90 – A) = sin B ⇒ 90 – A = B
∴ 90° = A + B

ప్రశ్న 168.
x = 2 cosec θ; y = 2 cot θ అయిన x² – y² విలువ ఎంత?
సాధన.
x = 2 cosec θ, y = 2 cot θ
x² – y² = (2 cosec θ)² – (2 cot θ)²
= 4 cosec² θ – 4 cot² θ
= 4 (cosec² θ – cot² θ)
= 4 (1) = 4

ప్రశ్న 169.
cos (A + B) = 0, cos B = \(\frac{\sqrt{3}}{2}\) అయిన A విలువను కనుగొనుము.
సాధన.
cos (A + B) = 0, cos B = \(\frac{\sqrt{3}}{2}\)
∴ A + B = 90° B = 30°
∴ A + 30° = 90° ⇒ A = 90° – 30 = 60°

ప్రశ్న 170.
\(\frac{\sqrt{1-\cos ^{2} \theta}}{\cos \theta}\) =
(A) \(\frac{\tan \theta}{1+\tan \theta}\)
(B) \(\frac{1}{\tan \theta}\)
(C) cot θ
(D) sin θ
జవాబు.
(D) sin θ

ప్రశ్న 171.
\(\frac{\sqrt{1-\cos ^{2} \theta}}{\cos \theta}\) =
(A) tan θ
(B) cos θ
(C) sec θ
(D) cot θ
జవాబు.
(A) tan θ

ప్రశ్న 172.
\(\frac{1}{\sqrt{1+\tan ^{2} \theta}}\) =
(A) sin θ
(B) cos θ
(C) sec θ
(D) cosec θ
జవాబు.
(B) cos θ

ప్రశ్న 173.
cos θ . tan θ =
(A) cos θ
(B) cot θ
(C) sin θ
(D) cos² θ

ప్రశ్న 174.
క్రింది పటం ∆ ABC లో ∠C = 45° మరియు ∠B = 90° అయిన cos A విలువ ఎంత?

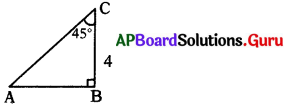
సాధన.
∆ ABC లో ∠B = 90° మరియు C = 45° కావున,
∴ ∠A = 45°; cos A = cos 45° = \(\frac{1}{\sqrt{2}}\)

ప్రశ్న 175.
sec² 33° – cot² 57° విలువను కనుగొనుము.
సాధన.
sec² 33° – cot² 57°
= sec² (90 – 57) – cot² 57° (∵ sec (90 – θ) = cosec θ)
= cosec² 57° – cot² 57°
= 1

ప్రశ్న 176.
√3 cot 2θ = 1 అయిన θ విలువను కనుగొనుము.
సాధన.
√3 cot 2θ = 1 ⇒ cot 2θ = \(\frac{1}{\sqrt{3}}\)
∴ 2θ = 60° (∵ cot 60° = \(\frac{1}{\sqrt{3}}\))
∴ θ = \(\frac{60^{\circ}}{2}\) = 30°

ప్రశ్న 177.
sin (log₁₀1) విలువ ఎంత ?
సాధన.
sin (log₁₀1)° = sin 0° = 0 (∵ log_a 1 = 0)

ప్రశ్న 178.
cos θ = 3 అయిన క్రింది వానిలో ఏది సత్యం ?
(A) θ = 60°
(B) cos\(\left(\frac{\theta}{2}\right)=\frac{\sqrt{3}}{2}\)
(C) sin\(\left(\frac{3 \theta}{4}\right)^{\circ}=\frac{1}{\sqrt{2}}\)
(D) పైవన్నీ
సాధన.
(D) పైవన్నీ

ప్రశ్న 179.
cos θ ను sin θ లో తెల్పండి.
సాధన.
cos θ = \(\sqrt{1-\sin ^{2} \theta}\)

ప్రశ్న 180.
cos 0° + sin 90° + √3 cosec 60° విలువను కనుగొనుము.
సాధన.
cos 0° + sin 90° + √3 cosec 60°

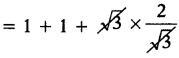
= 1 + 1 + 2 = 4

ప్రశ్న 181.
cos 60° ∙ cos 30° – sin60° ∙ sin30°విలువను కనుగొనుము.
సాధన.
cos 60° ∙ cos 30° – sin 60° ∙ sin 30°
= \(\frac{1}{2} \times \frac{\sqrt{3}}{2}-\frac{\sqrt{3}}{2} \times \frac{1}{2}=\frac{\sqrt{3}}{4}-\frac{\sqrt{3}}{4}\) = 0
(లేదా)
cos 60° ∙ Cos 30° – sin 60° ∙ sin 30
= cos (60 + 30)°
= cos 90° = 0
(∵cos (A + B) = cos A cos B – sin A sin B)

ప్రశ్న 182.
tan θ =
(A) \(\frac{1}{\cot \theta}\)
(B) \(\sqrt{\sec ^{2} \theta+1}\)
(C) \(\frac{\sin \theta}{\cos \theta}\)
(D) పైవన్నీ
జవాబు.
(D) పైవన్నీ

ప్రశ్న 183.
క్రింది త్రికోణమీతియ నిష్పత్తి విలువలకు సమానమపు సంవర్గమాన విలువను జత చేయండి.

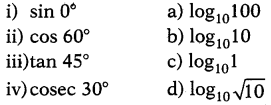
(A) i-b, ii-a, iii-c, iv-d.
(B) i-c, ii-d, iii-b, iv-a
(C) i-a, ii-c, iii-d, iv-b
(D) i-d, ii-c, iii-b, iv-a
జవాబు.
(D) i-d, ii-c, iii-b, iv-a

ప్రశ్న 184.
√3 tan θ = 1 అయిన 6 విలువ ఎంత ? (θ అల్పకోణము)
సాధన.
√3 tan θ = 1 ⇒ tan θ = \(\frac{1}{\sqrt{3}}\)
∴ θ = 30° (∴ tan 30° = \(\frac{1}{\sqrt{3}}\))

ప్రశ్న 185.
\(\sqrt{{cosec}^{2} \theta-\sin ^{2} \theta-\cos ^{2} \theta}\) ను ఒకే త్రికోణమితీయ నిష్పత్తిలో తెల్పండి.
సాధన.

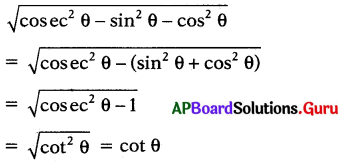
ప్రశ్న 186.
\(\sqrt{\frac{1-\cos ^{2} \theta}{1+\cot ^{2} \theta}}\) =
(A) sin θ
(B) sin θ
(C) sin θ
(D) sin⁴ θ
సాధన.
(C) sin θ
\(\sqrt{\frac{1-\cos ^{2} \theta}{1+\cot ^{2} \theta}}=\sqrt{\frac{\sin ^{2} \theta}{{cosec}^{2} \theta}}\)
= \(\sqrt{\sin ^{2} \theta \cdot \sin ^{2} \theta}\) = sin² θ

ప్రశ్న 187.
cosec 60° × cos 90° విలువ ఎంత ?
సాధన.
cosec 60° × cos 90° = \(\frac{2}{\sqrt{3}}\) × 0 = 0

ప్రశ్న 188.
sin 81° =
(A) cos 9°
(B) cos 81°
(C) – cos 9o
(D) cosec 81°
సాధన.
(A) cos 9°

ప్రశ్న 189.
tan θ = √3 అయితే sec θ విలువను కనుగోనుము
సాధన.
tan θ = √3 ⇒ θ = 60°
∴ sec θ = sec 60° = 2
(లేదా)
sec² θ = 1 + tan² θ
= 1 + (√3)² = 1 + 3 = 4
∴ sec θ = √4 = 2

ప్రశ్న 190.
cot²θ – \(\frac{1}{\sin ^{2} \theta}\) = – 1 అని చూపుము.
సాధన.
cot²θ – \(\frac{1}{\sin ^{2} \theta}\) = cot²θ – cosec²θ
= – (cosec² θ – cot² θ) = – 1

ప్రశ్న 191.
\(\frac{1}{\sec \theta-\tan \theta}\) = …………….
(A) sec θ – tan θ
(B) sec θ + tan θ
(C) sec²θ – tan²θ
(D) 1
జవాబు.
(B) sec θ + tan θ

ప్రశ్న 192.
sin 29° – cos 61° యొక్క విలువ ఎంత?
సాధన.
sin 29° – cos 61°
= sin (90 – 61)° – cos 61°
= cos 61° – cos 61° = 0

ప్రశ్న 193.
tan 1° ∙ tan 2° ∙ tan 3° ……….. tan 89° యొక్క విలువ ఎంత ?
సాధన.
tan 1° ∙ tan 2° ∙ tan 3°……….. tan 89°
= tan (90 – 89)° . tan (90 – 88)° ………. tan 45°….. tan 88° ∙ tan 89°
= cot 89° . cot 88°….. tan 45°….. tan 88° ∙ tan 89 = tan 45° = 1

ప్రశ్న 194.
క్రింది వానిలో సరైన ప్రవచనాలను ఎన్నుకొనుము.
(i) 0 ≤ θ ≤ 90 అయిన 0 ≤ sin θ ≤ 1
(ii) tan A = cot B (A, B లు అల్పకోణాలు) అయితే A + B = 90°
(iii) cosec θ = p, cot θ = q అయిన p² + q² = 1
(iv) cos θ = x అయిన sin θ = \(\sqrt{1+x^{2}}\).
సాధన.
(i) మరియు (ii) లు సత్యము.

ప్రశ్న 195.
పై 194 వ ప్రశ్నలో అసత్య ప్రవచనాలను గుర్తించి, వానిని సత్య ప్రవచనాలుగా మార్చండి.
సాధన.
(iii) మరియు (iv) లు అసత్య ప్రవచనాలు.
వానిని సత్య ప్రవచనాలుగా మార్చగా,
cosec θ = p, cot θ = q అయిన p² – q² = 1
cos θ = x అయిన sin θ = \(\sqrt{1-x^{2}}\)

ప్రశ్న 196.
tan (15° + B) = √3 అయితే B విలువ ఎంత?
సాధన.
tan (15° + B) = √3 ⇒ 15 + B = 60°
∴ B = 60° – 15° = 45°

ప్రశ్న 197.
క్రింది వానిలో ఏది sin e విలువ కావచ్చును ? .
(A) √2
(B) \(\frac{1}{\sqrt{2}}\)
(C) √3
(D) 2
సాధన.
B
(∵ √2 = 1.414 ….. > 1,
√3 = 1.732 ….. > 1
2 > 1)

ప్రశ్న 198.
\(\sqrt{(\sec \theta+1)(\sec \theta-1)}\) = tan θ అని చూపుము.
సాధన.
\(\sqrt{(\sec \theta+1)(\sec \theta-1)}\) = \(\sqrt{\sec ^{2} \theta-1}\)
= tan θ

ప్రశ్న 199.
cosec θ + cot θ = 2 అయిన cosec θ – cot θ విలువ ఎంత ?
సాధన.
cosec θ + cot θ = 2 అయిన
cosec θ – cot θ = \(\frac{1}{2}\)

ప్రశ్న 200.
క్రింది వానిలో cos θ విలువ కానిది ఏది ?
(A) \(\frac{3}{4}\)
(B) \(\frac{1}{2}\)
(C) \(\frac{4}{3}\)
(D) 0
జవాబు.
(C) \(\frac{4}{3}\)

ప్రశ్న 201.
క్రింది వానిలో ఏది సత్యం ?
(A) sin²θ + cos²θ = 1
(B) sin² θ = 1 – cos² θ
(C) cos² θ = 1 – sin² θ
(D) పైవన్నీ
జవాబు.
(D) పైవన్నీ

ప్రశ్న 202.
sin A = \(\frac{1}{\sqrt{2}}\), tan B = 1 అయిన క్రింది ఏది సత్యం ఏది సత్యం ? (A, B లు అల్పకోణాలు)
(i) A = B
(ii) A + B = 60°
(iii) sin (A + B) = 1
(iv) cos (A + B) = 1
(A) i మరియు ii
(B) i మరియు iii
(C) ii మరియు iv
(D) ii మరియు iii
జవాబు.
(B) i మరియు iii

ప్రశ్న 203.
క్రింది పటంలో AB పొడవును కనుగొనుము.

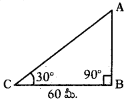
సాధన.
∆ABCలో ∠B = 90°
∴ tan 30° = \(\frac{\mathrm{AB}}{\mathrm{BC}}\) = \(\frac{A B}{60}\)
\(\frac{1}{\sqrt{3}}=\frac{\mathrm{AB}}{60}\) ⇒ AB = \(\frac{60}{\sqrt{3}}\) మీ.

ప్రశ్న 204.
క్రింది వానిలో ఏది నిర్వచింపబడదు”?
(A) sin 45°
(B) cot 0°
(C) tan 0°
(D) sec 45°
జవాబు.
(B) cot 0°

ప్రశ్న 205.
క్రింది వానిలో ఏది సత్యం ? ”
(A) sec²θ – tan²θ = 1
(B) sec²θ + tan²θ = 1
(c) tan²θ – sec² θ = 1
(D) పైవన్నీ
జవాబు.
(A) sec²θ – tan²θ = 1

ప్రశ్న 206.
A + B = 90° అయిన క్రింది వానిలో. ఏది సత్యం ?
(A) cos A = sin B
(B) tan A = cot B
(C) cosec A = sec A
(D) పైవన్నీ
జవాబు.
(D) పైవన్నీ

ప్రశ్న 207.
sec θ విలువ tan θ లో రాయండి.
సాధన.
sec²θ – tan² θ = 1
⇒ sec² 8 = 1 + tan²θ
⇒ sec θ = \(\sqrt{1+\tan ^{2} \theta}\).

ప్రశ్న 208.
జతపరుచుము.

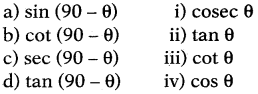
(A) a – iii, b-i, c – iv, d – ii
(B) a – iv, b – ii, c-i, d – iii
(C) a – iii, b-ii, c – iv, d-i
(D) a – iv, b – iii, c-ii, d – i
జవాబు.
(B) a – iv, b – ii, c-i, d – iii

ప్రశ్న 209.
A, Bలు అల్పకోణాలు మరియు ∠A ≥ ∠B అయిన క్రింది వానిలో ఏది అసత్యం ?
(A) sin A ≥ sin B
(B) cos A ≤ cos B
(C) tan A ≤ tan B
(D) sec A ≥ sec B
జవాబు.
C) tan A < tan B

ప్రశ్న 210.
cosec θ, cot θ లలో సర్వసమీకరణాన్ని రాయండి.
సాధన.
cosec²θ – cot- θ = 1

ప్రశ్న 211.
sin 75° + cos 65° ను 0° మరియు 45° ల మధ్యగల విలువలో రాయండి.
సాధన.
sin 75° + cos 65°
= sin (90 – 15)° + cos (90 – 25)
= cos 15° + sin 25°

ప్రశ్న 212.
sin 73° + tan 73°ను cos, cot నిష్పత్తుల విలువలలో రాయండి.
సాధన.
sin 73° + tan 73°
= sin (90 – 17)° + tan (90 – 17)°
= cos 17° + cot 17°

ప్రశ్న 213.
tan θ = p, sec θ = q అయిన p, q ల మధ్య సంబంధము ………………. .
(A) p² = 1 + q²
(B) q² = 1 + p²
(C) p² + q² = 1
(D) p²= 2q²
సాధన.
(B) q² = 1 + p²
sec² θ = 1 + tan²θ
∴ q² = 1 + p²

ప్రశ్న 214.
cosec θ = m, cot θ = n అయిన క్రింది వానిలో ఏది అసత్యం?
(A) m² – n² = 1
(B) sec θ = \(\frac{m}{n}\)
(C) cos θ = \(\frac{n}{m}\)
(D) m² + n² = 1
సాధన.
(A) m² – n² = 1
cosec² θ – cot² θ = 1
m² – n² = 1

ప్రశ్న 215.
sin θ = x అయిన cos θ ను x లో తెల్పండి.
సాధన.
cos θ = \(\sqrt{1-\sin ^{2} \theta}\) = \(\sqrt{1-x^{2}}\).
(∵ sin θ = x)

ప్రశ్న 216.
sin 0°, sin 60°, sin 30°, sin θ, sin 90° విలువల యొక్క మధ్యగతం \(\frac{1}{\sqrt{2}}\) అయ్యేటట్లు θ విలువను కనుగొనుము.
సాధన.
sin 0° = 0, sin 60° = \(\frac{\sqrt{3}}{2}\), sin 30° = \(\frac{1}{2}\),
sin 90° = 1, sin θ = ?
sin 0°, sin 60°, sin 30°, sin θ, sin 90° ల మధ్యగతము = \(\frac{1}{\sqrt{2}}\)
∴ sin θ = \(\frac{1}{\sqrt{2}}\) ⇒ θ = 45°
[విలువలను ఆరోహణాక్రమంలో రాయగా
0, \(\frac{1}{2}\), sin θ, \(\frac{\sqrt{3}}{2}\), 1.
sin θ, \(\frac{1}{2}\) మరియు \(\frac{\sqrt{3}}{2}\) ల మధ్య ఉన్నప్పుడే మధ్యగతం \(\frac{1}{\sqrt{2}}\) అయ్యే అవకాశం కలదు.)

ప్రశ్న 217.
sin 09°, sec 60°, cos 0°, tan 45° మరియు tan² θ విలువల యొక్క సగటు \(\frac{7}{5}\) మరియు \(\frac{1}{2}\) అల్పకోణము అయిన విలువ ఎంత ?
సాధన.
సగటు = \(\frac{\sin 0^{\circ}+\sec 60^{\circ}+\cos 0^{\circ}+\tan 45^{\circ}+\tan ^{2} \theta}{5}\)

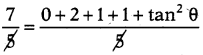
∴ 4 + tan² θ = 7 ⇒ tan² θ = 7 – 4 = 3
∴ tan θ = √3 ⇒ θ = 60°

ప్రశ్న 218.
sec θ + tan θ = x, sec θ – tan θ = y అయిన క్రింది వానిలో ఏది సత్యం ?
(i) xy = 1
(ii) \(\frac{x}{y}\) = 1
(iii) x² + y² = 1
(iv) x² – y² = 1
సాధన.
(i) సత్యం
(sec θ + tan θ) (sec θ – tan θ) = xy
sec²θ – tan² θ = 1
(∴ (a + b) (a – b) = a² – b²)
∴ x ∙ y = 1.

ప్రశ్న219.
∠A కు ఎదుటి భుజం ఏది ?
జవాబు :
∠A కు ఎదుటి భుజం = BC

ప్రశ్న220.
∠C కు ఆసన్న భుజమును తెల్పండి.
జవాబు :
∠C కు ఆసన్న భుజము = BC

ప్రశ్న221.
∠A + ∠C విలువ ఎంత ?
జవాబు :
∠A + ∠C = 90° [∵ ∠B = 90°, ∠A + ∠B + ∠C = 180°]

ప్రశ్న222.
\(\frac{\mathbf{B C}}{\mathbf{A B}}\) ని సూచించు ఏదేని ఒక త్రికోణమితీయ నిష్పత్తిని తెల్పండి.
జవాబు :
tan A (లేదా) cot C

ప్రశ్న223.
sin A = cos B అని నిరూపించండి.
జవాబు :
A + B = 90° ⇒ A = 90 – B
∴ sin A = sin (90 – B) = cos B [∵ sin (90 – θ) = cos θ]
∴ sin A = cos B

ప్రశ్న224.
\(\frac{\mathbf{B C}}{\mathbf{A C}}\) నిష్పత్తికి ప్రాతినిథ్యం వహించు త్రికోణమితీయ నిష్పత్తి
A) tan A
B) sin A
C) cos C
D) B మరియు C
జవాబు :
D) B మరియు C

ప్రశ్న 225.
క్రింది వానిలో ఏది సత్యం ?
A) AC > BC
B) AC > AB
C) A + C = 90°
D) పైవన్నీ
జవాబు :
D) పైవన్నీ

ప్రశ్న226.
sec 16. cosec 74° – cot 74° – tan 16° విలువ కనుగొనండి.
జవాబు :
0 (సున్న)

ప్రశ్న227.
x = 2019° అయితే sin² x + cos² x విలువ ఎంత ?
జవాబు :
x = 2019°, అయితే sin² x + cos² x = sin²2019° + cos²2019°
= 1 [∵ sin² θ + cos² θ = 1]

ప్రశ్న228.
x ఒక అల్పకోణము మరియు sin x = cos x అయితే x విలువ ఎంత ?
జవాబు :
ఇచ్చినది, sin x = cos x
sin (90°- θ) = cos θ మనకు తెలుసు.
cos x = sin(90° -x)
= sin x = sin(90° -x)
(గమనిక : sin A = sin B, అయితే A = B]
⇒ x = 90° – x
⇒ 2x = 90°
∴ x = 45°