Inter 1st Year Maths 1A Products of Vectors Formulas

Use these Inter 1st Year Maths 1A Formulas PDF Chapter 5 Products of Vectors to solve questions creatively.

Intermediate 1st Year Maths 1A Products of Vectors Formulas

Scalar or Dot Product of Two Vectors:
The scalar or dot product of two non – zero vectors $\bar{a}$ and $\bar{b}$, denoted by $\bar{a} \cdot \bar{b}$ is defined as $\bar{a} \cdot \bar{b}=|\bar{a}||\bar{b}|$ cos $(\bar{a}, \bar{b})$. This is a scalar, either $\bar{a}$ = 0 (or) $\bar{b}$ = 0, then we define $\bar{a} \cdot \bar{b}$ = 0. If we write $(\bar{a}, \bar{b})$ = 0, then $\bar{a} \cdot \bar{b}=|\bar{a}||\bar{b}|$ cos θ, if a ≠ 0, b ≠ 0, since 0 ≤ (a, b) = θ ≤ 7 80°, we get

0 ≤ θ < 90° ⇒ $\bar{a}$. b > 0.
θ = 90° ⇒ $\bar{a} \cdot \bar{b}$ = 0 and the vectors $\bar{a}$ and $\bar{b}$ are perpendicular.
90° < θ ≤ 180° ⇒ $\bar{a} \cdot \bar{b}$ < 0
$\bar{a} \cdot \bar{b}=\bar{b} \cdot \bar{a}$
a̅ (b̅ + c̅) = a̅ .b̅ + a̅ .c̅
If a̅, b̅ are parallel, a̅.b̅ = ± |a̅ | |b̅ |.
If l, m ∈ R, (la̅).(mb̅) = lm(a̅. b̅)
Projection of b̅ on a̅ (or) length of the projection a̅ = $\frac{|\bar{a} \cdot \bar{b}|}{|\bar{a}|}$
Orthogonal projection of b̅ on a̅ = $\frac{(\bar{a} \cdot \bar{b})_{\bar{a}}}{|\bar{a}|^{2}}$; a̅ ≠ 0
or
The projection vector b̅ on a̅ = $\left(\frac{\bar{a} \cdot \bar{b}}{|\bar{a}|^{2}}\right)$ a̅ and it is magnitude = $\frac{|\overline{\mathrm{a}} \cdot \overline{\mathrm{b}}|}{|\overline{\mathrm{a}}|}$
The component vector of b̅ along a̅ (or) parallel to a̅ is $\left(\frac{\bar{a} \cdot \bar{b}}{|\bar{a}|^{2}}\right)$a̅

Component vector of a̅ along b̅ = $\frac{(\bar{a} \cdot \bar{b}) \bar{b}}{|\bar{b}|^{2}}$, component vector of a̅ perpendicular to b̅ = a̅ – $\frac{(\bar{a} \cdot \bar{b}) \bar{b}}{|\bar{b}|^{2}}$

Orthogonal unit vectors :
Ifi, j, k are orthogonal unit vector triad in a right handed system, then

i̅ .j̅ = j̅.k̅ = k̅.i̅ = 0
i̅ .i̅ = j̅.j̅ = k̅.k̅ = 1
If r is any vector, r̅ = (r̅.i̅)i̅ +(r̅.j̅)j̅ ≠ (r̅.k̅)k̅

Some identities :
If a̅, b̅, c̅ are three vectors, then

(a̅ + b̅)² = |a̅|² + |b̅|² + 2(a̅ . b̅)
(a̅ – b̅)² = |a̅|² + |b̅|² – 2(a̅.b̅)
(a̅ + b̅)² + (a̅ – b̅)² = 2(|a̅|² + |b̅|²)
(a̅ + b̅)² – (a̅ – b̅)² = 4(a̅. b̅)
(a̅ + b̅). (a̅ – b̅) = |a̅|² – |b̅|²
(a̅ + b̅ + c̅)² = |a̅|² + |b̅|² + |c̅|² + 2(a̅ . b̅) + 2(b̅ . c̅) + 2(c̅ .a̅)

→ If a̅ = a₁ i̅ +a₂j̅ + a₃k̅ and b̅ = b₁i̅ + b₂j̅ + b₃k̅, then
a̅.b̅ = a₁b₁ + a₂b₂ + a₃b₃
a̅ is perpendicular to b̅
⇔ a₁b₁ + a₂b₂ + a₃b₃ = 0

→ |a̅| = , |b̅| = 

→ If (a̅, b̅) = then cos θ = $\frac{\bar{a} \cdot \bar{b}}{|\bar{a}||\bar{b}|}=\frac{a_{1} b_{1}+a_{2} b_{2}+a_{3} b_{3}}{\sqrt{\sum a_{1}^{2}} \sqrt{\sum b_{1}^{2}}}$ and sin θ = $\sqrt{\frac{\sum\left(a_{2} b_{3}-a_{3} b_{2}\right)^{2}}{\left(\sum a_{1}^{2}\right)\left(\sum b_{1}^{2}\right)}}$

→ a̅ is parallel to b̅ ⇔ a₁: b₁ = a₂ : b₂ = a₃: b₃

→ a̅.a̅ >0; |a̅.b̅| < |a̅| |b̅|
|a̅ + b̅| ≤ |a̅| + |b̅|; |a̅ – b̅| ≤ |a̅| + |b̅| ;
|a̅ – b̅| ≥ |a̅| – |b̅|

Vector equations of a plane :

The equation of the plane, whose perpendicular distance from the origin is p and whose unit normal drawn from the origin towards the plane is h is n̂ is r̅.n̂ = p.
Equation of a plane passing through the origin and perpendicular to the unit vector n̅, is r̅.n̅ = 0
Vector equation of a plane passing through a point A with position vector a and perpendicular to a vector n̅ is (r – a̅). n̅ = 0.

Perpendicular distance from the origin to the plane (r̅ – a̅).h = 0 is a̅. n̅ . where ‘a̅’ is the position vector of A in the plane and ‘n̅’ is a unit vector perpendicular to the plane.

Angle between two planes :
If π₁ and π₂2 be two planes and $\bar{M}_{1}, \bar{M}_{2}$ are normals drawn to them, we define the angle between M₁ and M₂ as the angle between π₁ and π₂. If the angle between  and  is θ, the angle between the given planes θ = cos^-1$\left[\frac{\bar{M}_{1} \cdot \bar{M}_{2}}{\left|\bar{M}_{1}\right|\left|\bar{M}_{2}\right|}\right]$

Work done by a constant force F:

If a constant force F̅ acting on a particle displaces it from a position ‘A’ to the position B, then the work done ‘W by this constant force T is the dot product of the vectors
representing the force F̅ and displacement $\overline{A B}$, i.e., W = F̅.$\overline{A B}$.
If F is the resultant of the forces F̅₁, F̅₂, ……………….F̅_n, then workdone in displacing the particle from A to B is
$\bar{W}=\bar{F}_{1} \cdot \overline{A B}+\bar{F}_{2} \cdot \overline{A B}+\ldots \ldots+F_{n} \cdot \overline{A B}$

Cross Product or Vector Product of two vectors :
The vector product or cross product of two non-parallel non – zero vectors ‘a̅’ and ‘b̅’ is defined as a̅ × b̅ = |a̅||b̅| sin θ n̂, where ‘ n̂’ is a unit vector perpendicular to the plane containing ‘a̅’ and ‘b̅’ such that a̅, b̅ and ‘n̂’ form a vector triad in the right handed system and (a̅, b̅) = θ, this is a vector. If either of a̅, b̅ is a zero vector or ‘a̅’ is parallel to ‘b̅’, we define a̅ × b̅ = 0.

Some important results on vector product:

|a̅ × b̅| = |a̅||b̅|sinθ ≤ |a̅||b̅| ;
|a̅ × b̅| = |b̅ × a̅|
a̅ × b̅ = -(b̅ × a̅):
-a̅ × -b̅ = a̅ × b̅
(-a̅) × b̅ = a̅ × (-b̅) – (a̅ × b̅)
la̅ × mb̅ = lm(a̅ × b̅) ;
a̅ × (b̅ + c̅) = a̅ × b̅ + a̅ × c̅
a̅ ≠ 0, b̅ ≠ 0 and a̅ × b̅ = 0 ⇔ ‘a̅’ and ‘b̅’ are parallel vectors.
a̅, b̅ , c̅ are non-zero vectors and a̅ × c̅ = b̅ × c̅ ⇒ either a̅ = b̅ or a̅ – b̅ is parallel to c̅.

Vector product among i. i and k:
If i̅, j̅ and k̅ are orthogonal unit vectors triad in the right handed system then

i̅ × j̅ = j̅ × j = k̅ × k̅ = 0
i̅ × j̅ = k̅ =-j̅ × i̅ ; j̅ × k̅ = k̅ × j̅ = i̅ ; k̅ × i̅ = -i̅ × k̅ = j̅
If a̅ = a₁ i̅ + a₂ j + a₃k ; b̅ = b₁i̅ + b₂ j̅ + b₃k̅, then
a̅ × b̅ = a₂b₃ – a₃b₂)i̅ + (a₃b₁ – a₁b₃)j̅ + (a₁b₂ – a₂b₁)k̅

This may be represented in the form of a determinants as a̅ × b̅ = $\left|\begin{array}{ccc}
\bar{i} & \bar{j} & \bar{k} \\
a_{1} & a_{2} & a_{3} \\
b_{1} & b_{2} & b_{3}
\end{array}\right|$

Unit vectors perpendicular to both ‘a̅’and ‘b̅’ are ± $\frac{\bar{a} \times \bar{b}}{|\bar{a} \times \bar{b}|}$
If a̅ = a₁i̅ + a₂j̅ + a₃k̅ ; b̅ = b₁i̅ + b₂ j̅ + b₃k̅ and (a̅, b̅) = θ, then
sin θ = $\frac{\sqrt{\sum\left(a_{2} b_{3}-a_{3} b_{2}\right)^{2}}}{\sqrt{\sum a_{1}^{2}} \sqrt{\sum b_{1}^{2}}}$ cos θ = $\frac{a_{1} b_{1}+a_{2} b_{2}+a_{3} b_{3}}{\sqrt{\sum a_{1}^{2}} \sqrt{\sum b_{1}^{2}}}$

Vector areas:

If $\overline{A B}=\bar{c}$ and $\overline{A C}=\bar{b}$ are two adjacent sides of a triangle ABC, then vector area of ΔABC = $\frac{1}{2}$(c̅ × b̅) and the area of the ΔABC = $\frac{1}{2}$|c̅ × b̅| $q. units.
If a̅, b̅, c̅ are the position vectors of A, B, C respectively then the vector area of
ΔABC = $\frac{1}{2}$[(b̅ × c̅) + (c̅ × a̅) + (a̅ × b̅)]
Area of ΔABC = $\frac{1}{2}$|(b̅ × c̅) + (c̅ × a̅) + (a̅ × b̅)|sq. units.
If  and  are the diagonals of a parallelogram ABCD, then the vector area of the parallelogram = $\frac{1}{2}$|a̅ × b̅| and area = $\frac{1}{2}$|a̅ × b̅|sq. units.
If AB = a̅ and AD = b̅ are two adjacent sides of a parallelogram ABCD, then its vector area = a̅ × b̅ and area = |a̅ × b̅| sq. units.
Vector area of the quadrilateral ABCD = $\frac{1}{2}$$(A C \times B D)$ and area of the quadrilateral ABCD = $\frac{1}{2}$$|\overline{A C} \times \overline{B D}|$sq. units.

Some useful formulas :

If a̅, b̅ are two non-zero and non-parallel vectors then
(a̅ × b̅)² = a²b² – (a̅.b̅)² = $\left|\begin{array}{cc}
a \cdot \bar{a} & \bar{a} \cdot \bar{b} \\
\bar{a} \cdot b & b \cdot \bar{b}
\end{array}\right|$
For any vector a̅,(a̅ × i̅)² + (a̅ × j̅)² + (a̅ × k̅)² = 2|a|²
If a̅, b̅, c̅ are the position vectors of the points A, B, C respectively, then the perpendicular distance from c to the line AB is $\frac{|\overline{A C} \times \overline{A B}|}{|\overline{A B}|}=\frac{|(\bar{b} \times \bar{c})+(\bar{c} \times \bar{a})+(\bar{a} \times \bar{b})|}{|b-\bar{a}|}$

Moment of a force :
Let 0 be the point of reference (origin) and $\overline{o p}=\bar{r}$ be the position vector of a point p on the line of action of a force F̅. Then the moment of the force F about 0 is given by r̅ × F̅.

Scalar triple product:
Let a̅, b̅, c̅ he three vectors. We call (a̅ × b̅). c̅ the scalar product of a̅, b and c. This is a scalar (real number). It is written as [a̅ b̅ c̅]

If (a̅ × b̅). c̅ = 0, then one or more of the vectors a̅, b̅ and c̅ should be zero vectors. If a ≠ 0, b ≠ 0, c ≠ 0, then c is perpendicular to a̅ × b̅. Hence the vector c̅ lies on the plane determined by a̅ and b̅. Hence a̅, b̅ and c̅ are coplanar.
If in a scalar triple product, any two vectors are parallel (equal), then the scalar triple product is zero i.e., [a̅ a̅ b̅] = [a̅ b̅ b̅] = [c̅ b̅ c̅] = 0.
In a scalar triple product remains unaltered if the vectors are permutted cyclically i.e., [a̅ b̅ c̅] = [b̅ c̅ a̅] = [c̅ a̅ b̅].
However [a̅ b̅ c̅] = -[b̅ a̅ c̅] = -[c̅ b̅ a̅] = -[a̅ c̅ b̅].
In a scalar triple product, the dot and cross are interchangeable i.e., a̅.b̅ × c̅ = a̅ × b̅.c̅

→ If i̅ , j̅ , k̅ are orthogonal unit vector triad in the right handed system, then

[i̅ j̅ k̅ ] = [j̅ k̅ i̅ ] = [k̅ i̅ j̅ ] = 1
[i̅ k̅ j̅ ] = [j̅ i̅ k̅ ] = [k̅ j̅ i̅ ] = -1
If a̅ = a₁ i̅ + a₂j̅ + a₃ k̅ ; b̅ = b₁i̅ + b₂ j̅ + b₃k̅ and c̅ = c₁i̅ + c₂ j̅ + c₃k̅ then [a̅ b̅ c̅] = $\left|\begin{array}{lll}
a_{1} & a_{2} & a_{3} \\
b_{1} & b_{2} & b_{3} \\
c_{1} & c_{2} & c_{3}
\end{array}\right|$

→ A necessary and sufficient condition that three non-parallel (non-collinear) and non-zero vectors a, b and c to be coplanar is [a̅ b̅ c̅] = 0. If [a̅ b̅ c̅] ≠ 0, then the three vectors are non-coplanar.

→ If a̅, b̅, c̅ are three non-zero, non-coplanar vectors and V is the volume of the parallelopiped with co-terminus edges a̅, b̅ and c̅, then v = |(a × b). c|. = |[a b c]|

→ The volume of the parallelopiped formed with A, B, C, D as vertices is $|[A B A C A D]|$ cubic units.

→ If a̅, b̅, c̅ represent the co-terminus edges of a tetrahedron, then its volume = $\frac{1}{6}$[a̅, b̅, c̅] cubic units.

→ If A(x₁ y₁ z₁], B(x₂, y₂, z₂] C(x₃ y₃ z₃) and D(x₄, y₄ z₄] are the vertices of a tetrahedron = $\frac{1}{6}$$|[A B A C A D]|$

Vector equation of a plane containing three non-collinear points a̅, b̅, c̅ is r̅ .[(b̅ × c̅) + (c̅ × a̅) + (a̅ × b̅)] = [a̅ b̅ c̅]
A unit vector perpendicular to the plane containing three non-collinear points a̅, b̅, c̅ is $\frac{(\bar{a} \times b)+(b \times \bar{c})+(\bar{c} \times \bar{a})}{|(\bar{a} \times \bar{b})+(b \times \bar{c})+(\bar{c} \times a)|}$
Length of the perpendicular from the origin to the plane containing three non-collinear points a̅, b̅, c̅ is $\frac{|[\bar{a} b c]|}{|(\bar{a} \times \bar{b})+(\bar{b} \times \bar{c})+(\bar{c} \times \bar{a})|}$

→ Vector equation of the plane passing through three non-collinear points a̅, b̅ and c̅ is [r̅ – a̅ b̅ – a̅ c̅ – a̅] = 0

→ Vector equation of the plane passing through a given point a̅ and parallel to the vectors b̅ and c̅ is [r b̅ c̅] = [a̅ b̅ c̅]

→ Vector equation of the line passing through the point a̅ and parallel to the vector b̅ is (r – a̅) × b̅ = 0

→ Distance of the point p(c) from a line joining the points A(a) and B(b) = |(c̅ – a̅) × b̅|
(25) i) Equation of the plane passing through the point p(x₁, y₁, z₁) and perpendicular to the vector ai̅ + bj̅ + ck̅ is a (x – x₁) + b(y – y₁) + c(z – z₁) = 0.

→ The equation of the plane passing through the points (x₁ y₁ z₁), (x₂, y₂, z₂) and
(x₃, y₃, z₃) is $\left|\begin{array}{ccc}
x-x_{1} & y-y_{1} & z-z_{1} \\
x_{2}-x_{1} & y_{2}-y_{1} & z_{2}-z_{1} \\
x_{3}-x_{1} & y_{3}-y_{1} & z_{3}-z_{1}
\end{array}\right|$ = 0

Skew lines:
Two lines l and m are called skew lines if there is no plane passing through these lines.

Shortest distance between the skew lines:
Shortest distance between the skew lines r̅ = a̅ + tb̅ and r̅ = c̅ + sd̅ is

Vector triple product:
If a̅, b̅ and c̅ are three vectors, products of the type (a̅ × b̅) × c̅, a̅ × (b̅ × c̅) from the vector triple products. From this definition.

If any one of a̅, b̅ and c̅ is a zero vector, a̅ × (b̅ × c̅) or (a̅ × b̅) c̅ = 0
If a̅ ≠ 0, b̅ ≠ 0, c̅ ≠ 0 and a̅ is parallel to b, then (a̅ × b̅) × c̅ = 0
If a̅ ≠ 0, b̅ ≠ 0, c̅ ≠ 0 and c̅ is perpendicular to the plane of a and b, then (a̅ × b̅) × c̅ = 0.

→ If a̅ ≠ 0, b̅ ≠ 0, c̅ ≠ 0, a̅ and b̅ are non-parallel vectors and c̅ is not perpendicular to the plane passing through a̅ and b, then
(a̅ × b̅) × c̅ = (a̅.c̅)b̅ – (b̅.c)a̅
a̅ × (b̅ × c̅) = (a̅.c̅)b̅ – (a.b̅)c̅

In general, vector triple product of three vectors need not satisfy the associative law. i.e., (a̅ × b) × c ≠ a̅ × (b × c)
For any three vectors a̅, b̅ and c
a̅ × (b̅ × c̅) + b̅ × (c̅ × a̅) + c̅ × (a̅ × b̅) = 0
[a̅ × b̅ b̅ × c̅ c̅ × a̅] = [a̅ b̅ c̅]²

Scalar product of four vectors :
Scalar product of a̅, b̅, c̅ and d̅ is () = (a̅. c̅) (b̅.d̅) – (a̅. d̅) (b̅ .c̅) = $\left|\begin{array}{ll}
\bar{a} \cdot \bar{c} & \bar{a} \cdot \bar{d} \\
\bar{b} \cdot \bar{c} & \bar{b} \cdot \bar{d}
\end{array}\right|$

Vector product of four vectors:
If a̅, b̅, c̅ and d̅ are four vectors,
(a̅ × b̅) × (c̅ × d̅) = [a̅ c̅ d̅] b̅ – [b̅ c̅ d̅]a̅ – [a b̅ d̅]c̅ – [a̅ b̅ c̅]d̅

Some important results:

[a̅ + b̅ b̅ + c̅ c̅ + a̅] = 2[a̅ b̅ c̅]
i̅ × (j̅ × k̅) + i̅ × (k̅ × i̅) + k̅ × (i̅ × j̅) = 0
[a̅ × b̅ b̅ × c̅ c̅ × a̅] = [a̅ b̅ c̅]²
[a̅ b̅ c̅] [l̅ m̅ n̅] = 
If a̅, b̅, c̅ be such that a is perpendicular to (b̅ + c̅), bis perpendicular to (c̅ + a̅), c̅ is perpendicular to (a̅ + b̅), then |a̅ + b̅ + c̅| = $\sqrt{a^{2}+b^{2}+c^{2}}$
If a line makes angles α, β, γ and δ with the diagonals of a cube, then
cos²α + cos²β + cos²γ + cos²δ = $\frac{4}{3}$
i̅ × (a̅ × i̅) + j̅ × (a̅ × j̅) + k̅ × (a̅ × k̅) – 2a̅

→ Equation of the sphere with centre at c and radius ‘a’ is r² – 2r̅. c̅ + c² = a²

Scalar Product
Def: Let $\vec{a}, \vec{b}$ be two vectors dot product (or) scalar product (or) direct product (or) inner product denoted by $\vec{a}, \vec{b}$. Which is defined as $|\vec{a}||\vec{b}|$cos θ where cos θ = $(\vec{a}, \vec{b})$
* The product $\vec{a}, \vec{b}$ is zero when $|\vec{a}|$ = 0 (or) $|\vec{b}|$ = 0 (or) θ = 90°.

Sign of the scalar product :
Let $\vec{a}, \vec{b}$ are two non-zero vectors

If θ is acute then $\vec{a}.\vec{b}$> 0 (i.e 0 < θ < 90°).
If θ is obtuse then $\vec{a}.\vec{b}$ < 0 (i.e 90° < θ < 180°).
If θ = 90° then$\vec{a} \cdot \vec{b}$ = o.
If θ = 0° then $\vec{a} \cdot \vec{b}=|\vec{a}||\vec{b}|$
If θ = 180° then $\vec{a} \cdot \vec{b}=|\vec{a}||\vec{b}|$

Note:

The dot product of two vectors is always scalar.
$\vec{a} \cdot \vec{b}=\vec{b} \cdot \vec{a}$ i.e dot product of two vectors is commutative.
If $\vec{a} \cdot \vec{b}$ are two vectors then $\vec{a} \cdot(-\vec{b})=(-\vec{a}) \cdot \vec{b}=-(\vec{a} \cdot \vec{b})$
$(-\vec{a}) \cdot(-\bar{b})=\vec{a} \cdot \vec{b}$
If l,m are two scalars and $\vec{a} \cdot \vec{b}$ are two vectors then $(l \bar{a}) \cdot(m \bar{b})={lm}(\vec{a} \cdot \vec{b})$
If $\vec{a}$ and $\vec{b}$ are two vectors then $\vec{a} \cdot \vec{b}=\pm|\vec{a}||\vec{b}|$
If $\vec{a}$ is a vector then $\vec{a} \cdot \vec{a}=|\vec{a}|^{2}$
If $\vec{a}$ is a vector $\vec{a}$.$\vec{a}$ is denoted by $\overline{(a)^{2}}$ hence $\overline{(a)^{2}}=|\vec{a}|^{2}$

Components and orthogonal projection:
Def: Let $\vec{a}=\overline{O A} \quad \vec{b}=\overline{O B}$ be two non zero vectors let the plane passing through B and perpendicular to a intersect $\overline{O A}$ ln M.

If $(\vec{a}, \vec{b})$ is acute then OM is called component of $\vec{b}$ on $\vec{a}$.
If $(\vec{a}, \vec{b})$ is obtuse then -(OM) is called the component of $\vec{b}$ on $\vec{a}$.
The vector $\overline{O M}$ is called component vector of $\vec{b}$ on $\vec{a}$.

Inter 1st Year Maths 1A Products of Vectors Formulas 1

Def: Let $\vec{a}=\overline{O A}$; $\vec{b}=\overrightarrow{P Q}$ be two vectors let the planes passing through P, Q and perpendicular to a intersect $[latex]$[/latex] in L, M respectively then $\overline{L M}$ is called orthogonal projection of $\vec{b}$ on $\vec{a}$
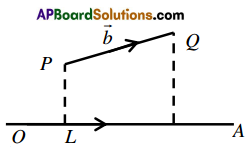
Inter 1st Year Maths 1A Products of Vectors Formulas 2

Note:

The orthogonal projection of a vector b on a is equal tb component vector of b on a .
Component of a vector $\vec{b}$ on $\vec{a}$ is also called projection of $\vec{b}$ on $\vec{a}$
If A< B, C, D are four points in the space then the component of $\overline{A B}$ on $\overline{C D}$ is same as the projection of $\overline{A B}$ on the ray $\overline{C D}$.

→ If $\vec{a}, \vec{b}$ be two vectors ($\vec{a} \neq \vec{o}$) then

The component of $\vec{b}$ on $\vec{a}$ is $\frac{\vec{b} \cdot \vec{a}}{|\vec{a}|}$
The orthogonal projection of $\vec{b}$ on $\vec{a}$ is $\frac{(\vec{b} \cdot \vec{a}) \vec{a}}{|\vec{a}|^{2}}$

→ If $\vec{i}, \vec{j}, \vec{k}$ form a right handed system of Ortho normal triad then

$\vec{i} \cdot \vec{j}=\vec{j} \cdot \vec{j}=\vec{k} \cdot \vec{k}$ = 1
$\vec{i} \cdot \vec{j}=\vec{j} \cdot \vec{i}=0 ; \vec{j} \cdot \vec{k}=\vec{k} \cdot \vec{j}=0 ; \vec{k} \cdot \vec{i}=\vec{i} \cdot \vec{k}=0$

→ If $\vec{a}=a_{1} \vec{i}+a_{2} \vec{j}+a_{3} \vec{k}$ $\vec{b}=b_{1} \vec{i}+b_{2} \vec{j}+b_{3} \vec{k}$ then $\vec{a} \cdot \vec{b}=a_{1} b_{1}+a_{2} b_{2}+a_{3} b_{3}$

→ If $\vec{a}, \vec{b}, \vec{c}$ are three vectors then
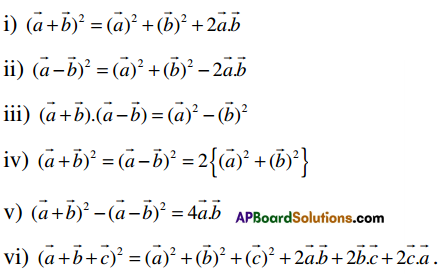
Inter 1st Year Maths 1A Products of Vectors Formulas 3

→ If $\vec{r}$ is vector then $\vec{r}=(\vec{r} \cdot \vec{i}) i+(\vec{r}+\vec{j}) \vec{j}+(\vec{r} \cdot \vec{k}) \vec{k}$

Angle between the planes:
The angle between the planes is defined as the angle between the normals to the planes drawn from any point in the space.

Sphere:
The vector equation of a sphere with centre C having position vector $\vec{c}$ and radius a is $(\vec{r}-\vec{c})^{2}$ = a² i.e. $\vec{r}^{2}-2 \vec{r} \cdot \vec{c}+c^{2}$ = a²

The vector equation of a sphere with A(a) and B(b) as the end points of a diameter is $(\vec{r}-\vec{a}) \cdot(\vec{r}-\vec{b})$ = 0 (or) $(\vec{r})^{2}-\vec{r} \cdot(\vec{a}+\vec{b})+\vec{a} \cdot \vec{b}$ = 0

Work done by a force :
If a force $\vec{F}$ acting on a particle displaces it from a position A to the position B then work done W by this force $\vec{F}$ is $\vec{F} \cdot \overline{A B}$

The vector equation of the plane which is at a distance of p from the origin along the unit vector $\vec{n}$ is $\vec{r} \cdot \vec{n}$ = p.
The vector equation of the plane passing through the origin and perpendicular to the vector m is r.m =0
The Cartesian equation of the plane which is at a distance of p from the origin along the unit vector n = li + mj + nk of the plane is n = lx + my + nz
The vector equation of the plane passing through the point a having position vector $\vec{a}$ and perpendicular to the vector $\vec{m}$ is $(\vec{r}-\vec{a}) \cdot \vec{m}$ = 0.
The vector equation of the plane passing through the point a having position vector $\vec{a}$ and parallel to the plane r.m=q is $(\vec{r}-\vec{a}) \cdot \vec{m}$ = 0.

Cross( Vector) Product of Vectors:
Let $\vec{a}, \vec{b}$ be two vectors. The cross product or vector product or skew product of vectors $\vec{a}, \vec{b}$ is denoted by $\vec{a} \times \vec{b}$ and is defined as follows

If $\vec{a}$ = 0 or $\vec{b}$ = 0 or $\vec{a}, \vec{b}$ are parallel then $\vec{a} \times \vec{b}$ = 0
If $\vec{a}$ ≠ 0, $\vec{b}$ ≠ 0, $\vec{a}, \vec{b}$ are not parallel then $\vec{a} \times \vec{b}=|\vec{a}||\vec{b}|(\sin \theta) \vec{n}$ where $\vec{n}$ is a unit vector perpendicular to a and b so that a, b, n form a right handed system.

Note:

$\vec{a} \times \vec{b}$ is a vector
If $\vec{a}, \vec{b}$ are not parallel then $\vec{a} \times \vec{b}$ is perpendicular to both a and b
If $\vec{a}, \vec{b}$ are not parallel then $\vec{a}, \vec{b}$ , $\vec{a} \times \vec{b}$ form a right handed system .
For any vector $\vec{a}$ $\vec{a} \times \vec{b}$ = o

2. If $\vec{a}, \vec{b}$ are two vectors $\vec{a} \times \vec{b}=-\vec{b} \times \vec{a}$ this is called “anti commutative law”

3. If $\vec{a}, \vec{b}$ are two vectors then $\vec{a} \times(-\vec{b})=(-\vec{a}) \times \vec{b}=-(\vec{a} \times \vec{b})$

4. If $\vec{a}, \vec{b}$ are two vectors then $(-\vec{a}) \times(-\vec{b})=\vec{a} \times \vec{b}$

5. If $\vec{a}, \vec{b}$ are two vectors l,m are two scalars then (la) x (mb) = lm(a x b)

6. If $\vec{a}, \vec{b}, \vec{b}$ are three vectos, then

$\vec{a} \times(\vec{b}+\vec{c})=\vec{a} \times \vec{b}+\vec{a} \times \vec{c}$
$(\vec{b}+\vec{c}) \times \vec{a}=\vec{b} \times \vec{a}+\vec{c} \times \vec{a}$

7. If $\vec{l}, \vec{l}, \vec{k}$ from a right handed system of orthonormal triad then

$\vec{l} \times \vec{l}=\vec{j} \times \vec{j}=\vec{k} \times \vec{k}=\vec{o}$
$\vec{i} \times \vec{j}=\vec{k}=-\vec{j} \times \vec{l} ; \vec{j} \times \vec{k}=\vec{l}=-\vec{k} \times \vec{j} ; \vec{k} \times \vec{l}=\vec{j}=-\vec{l} \times \vec{k}$

→ If $\vec{a}=a_{1} \vec{l}+a_{2} \vec{j}+a_{3} \vec{k}, \vec{b}=b_{1} \vec{l}+b_{2} \vec{j}+b_{3} \vec{k}$ then $\vec{a} \times \vec{b}=\left|\begin{array}{ccc}
\vec{l} & \vec{j} & \vec{k} \\
a_{1} & a_{2} & a_{3} \\
b_{1} & b_{2} & b_{3}
\end{array}\right|$

→ If $\vec{a}=a_{1} \vec{l}+a_{2} \vec{m}+a_{3} \vec{n}, \quad \vec{b}=b_{1} \vec{l}+b_{2} \vec{m}+b_{3} \vec{n}$ where $\vec{l}, \vec{m}, \vec{n}$ form a right system of non coplanar vectors then 

→ If $\vec{a}, \vec{b}$ are two vectors then $(\vec{a} \times \vec{b})^{2}+(\vec{a} \cdot \vec{b})^{2}$ = a²b².

Vector Area:
If A is the area of the region bounded by a plane curve and $\vec{n}$ is the unit vector perpendicular to the plane of the curve such that the direction of curve drawn can be considered anti clock wise then A$\vec{n}$ is called vector area of the plane region bounded by the curve.

The vector area of triangle ABC is $\frac{1}{2} \overline{A B} \times \overrightarrow{A C}=\frac{1}{2} \overrightarrow{B C} \times \overrightarrow{B A}=\frac{1}{2} \overline{C A} \times \overrightarrow{C B}$
If $\vec{a}, \vec{b}, \vec{c}$are the position vectors of the vertices of a triangle then the vector area of the triangle is $\frac{1}{2}(\vec{a} \times \vec{b}+\vec{b} \times \vec{c}+\vec{c} \times \vec{a})$
If ABCD is a parallelogram and $\overrightarrow{A B}=\vec{a}, \quad \overrightarrow{B C}=\vec{b}$ then the vector area of ABCD is $\vec{a} \times \vec{b}$.
If ABCD is a parallelogram and $\overrightarrow{A C}=\vec{a}, \overrightarrow{B C}=\vec{b}$ then vector area of parallelogram ABCD is $\frac{1}{2}(\vec{a} \times \vec{b})$
The vector equation of a line passing through the point A with position vector a and perpendicular to the vectors $\vec{b} \times \vec{c}$ is $\vec{r}=\vec{a}+t(\vec{b} \times \vec{c})$.

Scalar Triple Product:

If $\vec{a}, \vec{b}, \vec{c}$ are the three vectors, then the real numbers $(\vec{a} \times \vec{b}) \cdot \vec{c}$ is called scalar triple product denoted by $[\vec{a} \vec{b} \vec{c}]$. This is read as ‘box’ $\vec{a}, \vec{b}, \vec{c}$
If V is the volume of the parallelepiped with coterminous edges a, b, c then V = |$[\vec{a} \vec{b} \vec{c}]$|
If $\vec{a}, \vec{b}, \vec{c}$ form the right handed system of vectors then V = $[\vec{a} \vec{b} \vec{c}]$
If $\vec{a}, \vec{b}, \vec{c}$ form left handed system of vectors then -V = $[\vec{a} \vec{b} \vec{c}]$

Note:

The scalar triple product is independent of the position of dot and cross. i.e. $\vec{a} \times \vec{b} \cdot \vec{c}=\vec{a} \cdot \vec{b} \times \vec{c}$
The value of the scalar triple product is unaltered so long as the cyclic order remains unchanged
$[\vec{a} \vec{b} \vec{c}]=[\vec{b} \vec{c} \vec{a}]=[\vec{c} \vec{a} \vec{b}]$
The value of a scalar triple product is zero if two of its vectors are equal
$[\vec{a} \vec{a} \vec{b}]$= 0 $[\vec{b} \vec{b} \vec{c}]$ = 0
If a, b, c are coplanar then $[\vec{a} \vec{b} \vec{c}]$ = 0
If a,b,c form right handed system then $[\vec{a} \vec{b} \vec{c}]$ > 0
If a,b,c form left handed system then $[\vec{a} \vec{b} \vec{c}]$ < 0
The value of the triple product changes its sign when two vectors are interchanged
$[\vec{a} \vec{b} \vec{c}]$ = –$[\vec{a} \vec{c} \vec{b}]$
If l,m, n are three scalars $\vec{a}, \vec{b}, \vec{c}$ are three vectors then

→ Three non zero non parallel vectors abc nare coplanar iff $[l \vec{a} m \vec{b} \quad n \vec{c}]={lmn}\left[\begin{array}{lll}
\vec{a} & \vec{b} & \vec{c}
\end{array}\right]$= 0

→ If $\vec{a}=a_{1} \vec{l}+a_{2} \vec{m}+a_{3} \vec{n}, \vec{b}=b_{1} \vec{l}+b_{2} \vec{m}+b_{3} \vec{n}, \vec{c}=c_{1} \vec{l}+c_{2} \vec{m}+c_{3} \vec{n}$ where $\vec{l}, \vec{m}, \vec{n}$ form a right handed system of non coplanar vectors, then $[\vec{a} \vec{b} \vec{c}]=\left|\begin{array}{ccc}
\vec{m} \times \vec{n} & \vec{n} \times \vec{l} & \vec{l} \times \vec{m} \\
b_{1} & b_{2} & b_{3} \\
c_{1} & c_{2} & c_{3}
\end{array}\right|$

→ The vectors equation of plane passing through the points A, B with position vectors $\vec{a}, \vec{b}$ and parallel to the vector $\vec{c}$ is $[\vec{r}-\vec{a} \vec{b}-\vec{a} \vec{c}]$ (or) $[\vec{r} \vec{b} \vec{c}]+[\vec{r} \vec{c} \vec{a}]=\left[\begin{array}{lll}
\vec{a} & \vec{b} & \vec{c}
\end{array}\right]$

→ The vector equation of the plane passing through the point A with position vector $\vec{a}$ and parallel to $\vec{b}, \vec{c}$ is $[\vec{r}-\vec{a} \vec{b} \vec{c}]$ = 0 i.e. $\left[\begin{array}{lll}
\vec{r} & \vec{b} & \vec{c}
\end{array}\right]=\left[\begin{array}{lll}
\vec{a} & \vec{b} & \vec{c}
\end{array}\right]$

Skew lines:
Two lines are said to be skew lines if there exist no plane passing through them i.e. the lines lie on two difference planes
Def:- l₁ and l₂ are two skew lines. If P is a point on l₁ and Q is a point on l₂ such that $\overleftarrow{P Q}$ ⊥ l₁ and PQ ⊥ l₂ then $\overleftarrow{P Q}$ is called shortest distance and $\overleftarrow{P Q}$ is called shortest distance line between the lines l₁ and l₂.

The shortest distance between the skew lines $\vec{r}=\vec{a}+t \vec{b}$ and $\vec{r}=\vec{c}+t \vec{d}$ is $\frac{|[\vec{a}-\vec{c} \vec{b} \vec{d}]|}{|\vec{b} \times \vec{d}|}$

Vector Triple Product:
Cross Product of Three vectors : For any three vectors $\bar{a}, \bar{b}$ or $\bar{c}$ then cross product or vector product of these vectors are given as $\bar{a} \times(\bar{b} \times \bar{c}),(\bar{a} \times \bar{b}) \times \bar{c}$ or $(\bar{b} \times \bar{c}) \times \bar{a}$ etc.
Inter 1st Year Maths 1A Products of Vectors Formulas 4
vi. If $\bar{a}, \bar{b}$ or $\bar{c}$ are non zero vectors and  then b and c are parallel (or collinear) vectors.

vii. If $\bar{a}, \bar{b}$ or $\bar{c}$ are non zero and non parallel vectors then $\bar{a} \times(\bar{b} \times \bar{c}), \quad \bar{b} \times(\bar{c} \times\bar{a})$ and $\bar{c} \times(\bar{a} \times \bar{b})$ are non collinear vectors.

viii. If $\bar{a}, \bar{b}$ or $\bar{c}$ are any three vectors then $\bar{a}(\bar{b} \times \bar{c})+\bar{b} \times(\bar{c} \times \bar{a})+\bar{c} \times(\bar{a} \times \bar{b})=\overline{\mathrm{O}}$

ix. If $\bar{a}, \bar{b}$ or $\bar{c}$ are any three vectors then $\bar{a}(\bar{b} \times \bar{c})+\bar{b} \times(\bar{c} \times \bar{a})+\bar{c} \times(\bar{a} \times \bar{b})$ are coplanar. [since sum of these vectors is zero]

x. $\bar{a}(\bar{b} \times \bar{c})$ is vector lies in the plane of $\bar{b}$ and $\bar{c}$ or parallel to the plane of $\bar{b}$ and $\bar{c}$.

Product of Four Vectors:
Dot product of four vectors : The dot product of four vectors a̅, b̅, c̅ and d̅ is given as $(\bar{a} \times \bar{b}) \cdot(\bar{c} \times \bar{d})=(\bar{a} \cdot \bar{c})(\bar{b} \cdot \bar{d})-(\bar{a} \cdot \bar{d})(\bar{b} \cdot \bar{c})=\left|\begin{array}{ll}
\bar{a} \cdot \bar{c} & \bar{a} \cdot \bar{d} \\
\bar{b} \cdot \bar{c} & \bar{b} \cdot \bar{d}
\end{array}\right|$

→ Cross product of four vectors : If a̅, b̅, c̅ and d̅ are any four vectors then
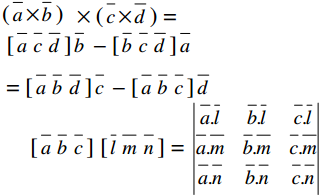
Inter 1st Year Maths 1A Products of Vectors Formulas 5

→ The vectorial equation of the plane passing through the point a and parallel to the vectors b̅, c̅is $[\overline{\mathrm{r}} \overline{\mathrm{b}} \overline{\mathrm{c}}]=[\overline{\mathrm{a}} \overline{\mathrm{b}} \overline{\mathrm{c}}]$

→ The vectorial equation of the plane passing through the points a̅, b̅ and parallel to the vector c̅ is $[\overline{\mathrm{rb}} \overline{\mathrm{c}}]+[\overline{\mathrm{r}} \overline{\mathrm{c}} \overline{\mathrm{a}}]=[\overline{\mathrm{a}} \overline{\mathrm{b}} \overline{\mathrm{c}}]$

→ The vectorial equation of the plane passing through the points a̅, b̅, c̅ is $[\overline{\mathrm{r}} \overline{\mathrm{b}} \overline{\mathrm{c}}]+[\overline{\mathrm{r}} \overline{\mathrm{c}} \overline{\mathrm{a}}]+[\overline{\mathrm{ra}} \overline{\mathrm{b}}]=[\overline{\mathrm{a}} \overline{\mathrm{b}} \overline{\mathrm{c}}]$

→ If the points with the position vectorsa̅, b̅, c̅, d̅ are coplanar, then the condition is $[\overline{\mathrm{a}} \overline{\mathrm{bd}}]+[\overline{\mathrm{b}} \overline{\mathrm{c}} \overline{\mathrm{d}}]+[\overline{\mathrm{c}} \overline{\mathrm{a}} \overline{\mathrm{d}}]=[\overline{\mathrm{a}} \overline{\mathrm{b}} \overline{\mathrm{c}}]$

→ Length of the perpendicular from the origin to the plane passing through the points a̅, b̅, c̅ is $\frac{|[\overline{\mathrm{a} b} \overline{\mathrm{c}}]|}{|\overline{\mathrm{b}} \times \overline{\mathrm{c}}+\overline{\mathrm{c}} \times \overline{\mathrm{a}}+\overline{\mathrm{a}} \times \overline{\mathrm{b}}|}$

→ Length of the perpendicular from the point c̅ on to the line joining the points a̅, b̅ is $\frac{\mid(\overline{\mathrm{a}}-\overline{\mathrm{c}}) \times(\overline{\mathrm{c}}-\overline{\mathrm{b}})}{|\overline{\mathrm{a}}-\overline{\mathrm{b}}|}$

→ P, Q, R are non collinear points. Then distance of P to the plane OQR is OP. $\left|\frac{\overline{\mathrm{OP}} \cdot(\overline{\mathrm{OQ}} \times \overline{\mathrm{OR}})}{|\overline{\mathrm{OQ}} \times \overline{\mathrm{OR}}|}\right|$

→ Perpendicular distance from P(α̅ ) to the plane passing through A(a̅) and parallel to the vectors b and c is
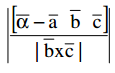
Inter 1st Year Maths 1A Products of Vectors Formulas 6

→ Length of the perpendicular from the point c̅ to the line $\overline{\mathrm{r}}=\overline{\mathrm{a}}+\mathrm{tb}$ is $\frac{|(\overline{\mathrm{c}}-\overline{\mathrm{a}}) \times \overline{\mathrm{b}}|}{|\overline{\mathrm{b}}|}$