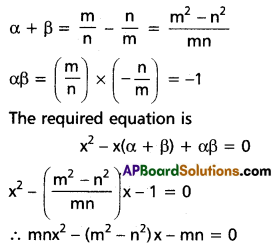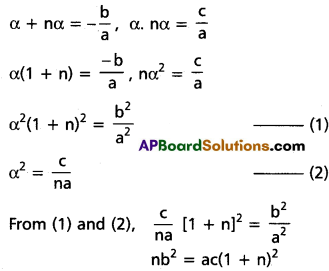Category: Inter 2nd Year

Practicing the Intermediate 2nd Year Maths 2A Textbook Solutions Inter 2nd Year Maths 2A Theory of Equations Solutions Exercise 4(b) will help students to clear their doubts quickly.

Intermediate 2nd Year Maths 2A Theory of Equations Solutions Exercise 4(b)

I.

Question 1.
Solve x³ – 3x² – 16x + 48 = 0, given that the sum of two roots is zero.
Solution:
Let α, β, γ are the roots of x³ – 3x² – 16x + 48 = 0
α + β + γ = 3
Given α + β = 0 (∵ Sum of two roots is zero)
∴ γ = 3
i.e. x – 3 is a factor of x³ – 3x² – 16x + 48 = 0

x² – 16 = 0
⇒ x² = 16
⇒ x = ±4
∴ The roots are -4, 4, 3

Question 2.
Find the condition that x³ – px² + qx – r = 0 may have the sum of its roots zero.
Solution:
Let α, β, γ be the roots of x³ – px² + qx – r = 0
α + β + γ = p ………(1)
αβ + βγ + γα = q ………..(2)
αβγ = r ………..(3)
Given α + β = 0 (∵ Sum of two roots is zero)
From (1), γ = p
∴ γ is a root of x³ – px² + qx – r = 0
γ³ – pγ² + qγ – r = 0
But γ = p
p³ – p(p²) + q(p) – r = 0
p³ – p² + qp – r = 0
∴ qp = r is the required condition.

Question 3.
Given that the roots of x³ + 3px² + 3qx + r = 0 are in
(i) A.P., show that 2p³ – 3qp + r = 0
(ii) G.P., show that p³r = q³
(iii) H.P., show that 2q³ = r(3pq – r)
Solution:
Given equation is x³ + 3px² + 3qx + r = 0
(i) The roots are in A.P.
Suppose a – d, a, a + d are the roots
Sum = a – d + a + a + d = -3p
⇒ 3a = -3p
⇒ a = -p ……….(1)
∵ ‘a’ is a root of x³ + 3px² + 3qx + r = 0
⇒ a³ + 3pa² + 3qa + r = 0
But a = -p
⇒ p³ + 3p(-p)² + 3q(-p) + r = 0
⇒ 2p³ – 3pq + r = 0 is the required condition

(ii) The roots are in G.P.
Suppose the roots be \(\frac{a}{R}\), a, aR
Given (\(\frac{a}{R}\)) (a) (aR) = -r
⇒ a = -r
⇒ a = (-r)^1/3
∵ ‘a’ is a root of x³ + 3px² + 3qx + r = 0
⇒ (-r^1/3)³ + 3p(-r^1/3)² + 3q(-r^1/3) + r = 0
⇒ -r + 3pr^2/3 – 3qr^1/3 + r = 0
pr^2/3 = qr^1/3
⇒ pr^1/3 = q
⇒ p^1/3r = q is the required condition

(iii) The roots of x³ + 3px² + 3qx + r = 0 are in H.P.
x³ + 3px² + 3qx + r = 0 ……..(1)
Let y = \(\frac{1}{x}\) so that \(\frac{1}{y^{3}}+\frac{3 p}{y^{2}}+\frac{3 q}{y}+r\) = 0
Roots of ry³ + 3qy² + 3py + 1 = 0 are in A.P.
ry³ + 3qy² + 3py + 1 = 0 ……..(2)
Suppose a – d, a, a + d be the roots of (2)
Sum = a – d + a + a + d = \(-\frac{3 q}{r}\)
3a = \(-\frac{3 q}{r}\)
a = \(-\frac{q}{r}\) ………(1)
∵ ‘a’ is a root of ry³ + 3qy² + 3py + 1 = 0
⇒ ra³ + 3qa² + 3pa + 1 = 0
But a = \(-\frac{q}{r}\)
⇒ \(r\left(-\frac{q}{r}\right)^{3}+3 q\left(-\frac{q}{r}\right)^{2}+3 p\left(-\frac{q}{r}\right)+1=0\)
⇒ \(\frac{-q^{3}}{r^{2}}+\frac{3 q^{3}}{r^{2}}-\frac{3 p q}{r}+1=0\)
⇒ -q³ + 3q³ – 3pqr + r² = 0
⇒ 2q³ = r(3pq – r) is the required condition.

Question 4.
Find the condition that x³ – px² + qx – r = 0 may have the roots in G.P.
Solution:
Let \(\frac{a}{R}\), a, aR be the roots of x³ – px² + qx – r = 0
The product of the roots = \(\frac{a}{R}\) . a . aR = a³
product of the roots = r
⇒ a = r^1/3
∵ a is a root of x³ – px² + qx – r = 0
⇒ a³ – pa² + qa – r = 0
But a = r^1/3
⇒ (r^1/3)³ – p(r^1/3)² + q(r^1/3) – r = 0
⇒ r – p . r^2/3 + q . r^1/3 – r = 0
⇒ p . r^2/3 = qr^1/3
By cubing on both sides
⇒ p³r² = q³r
⇒ p³r = q³ is the required condition

II.

Question 1.
Solve 9x³ – 15x² + 7x – 1 = 0, given that two of its roots are equal.
Solution:
Suppose α, β, γ are the roots of 9x³ – 15x³ + 7x – 1 = 0
α + β + γ = \(\frac{15}{9}=\frac{5}{3}\)
αβ + βγ + γα = \(\frac{7}{9}\)
αβγ = \(\frac{1}{9}\)
Given α = β (∵ two of its roots are equal)
2α + γ = \(\frac{5}{3}\)
⇒ γ = \(\frac{5}{3}\) – 2α
α² + 2αγ = \(\frac{7}{9}\)
⇒ α² + 2α (\(\frac{5}{3}\) – 2α) = \(\frac{7}{9}\)
⇒ α² + \(\frac{2 \alpha(5-6 \alpha)}{3}=\frac{7}{9}\)
⇒ 9α² + 6α(5 – 6α) = 7
⇒ 9α² + 30α – 36α² = 7
⇒ 27α² – 30α + 7 = 0
⇒ (3α – 1)(9α – 7) = 0
⇒ α = \(\frac{1}{3}\) or \(\frac{7}{9}\)

The roots are \(\frac{1}{3}\), \(\frac{1}{3}\), 1

Question 2.
Given that one root of 2x³ + 3x² – 8x + 3 = 0 is double of another root, find the roots of the equation.
Solution:
Suppose α, β, γ are the roots of 2x³ + 3x² – 8x + 3 = 0
α + β + γ = \(-\frac{3}{2}\) ……..(1)
αβ + βγ + γα = -4 ……..(2)
αβγ = \(-\frac{3}{2}\)
Given α = 2β (∵ one root is double the other)
Substituting in (1)
3β + γ = \(-\frac{3}{2}\)
⇒ γ = \(-\frac{3}{2}\) – 3β …….(4)
Substituting in (2)
αβ + γ(α + β) = -4
⇒ 2β² + 3βγ = -4
⇒ 2β² + 3β(\(-\frac{3}{2}\) – 3β) = -4
⇒ 2β² – \(\frac{3 \beta(3+6 \beta)}{2}\) = -4
⇒ 4β² – 9β – 18β² = -8
⇒ 14β² + 9β – 8 = 0
⇒ (2β – 1)(7β + 8) = 0
⇒ 2β – 1 = 0 or 7β + 8 = 0
⇒ β = \(\frac{1}{2}\) or β = \(-\frac{8}{7}\)

∴ The roots are \(\frac{1}{2}\), 1 and -3

Question 3.
Solve x³ – 9x² + 14x + 24 = 0, given that two of the roots are in the ratio 3 : 2.
Solution:
Suppose α, β, γ are the roots of x³ – 9x² + 14x + 24 = 0
α + β + γ = 9 ………(1)
αβ + βγ + γα = 14 ……….(2)
αβγ = -24 ……….(3)
∵ two roots are in the ratio 3 : 2
Let α : β = 3 : 2
⇒ β = \(\frac{2 \alpha}{3}\)
Substituting in (1)
\(\frac{5 \alpha}{3}\) + γ = 9
⇒ γ = 9 – \(\frac{5 \alpha}{3}\) ………(4)
Substituting in (2)
⇒ \(\frac{2}{3}\) α² + γ(α + β) = 14
⇒ \(\frac{2}{3} \alpha^{2}+\left(9-\frac{5 \alpha}{3}\right) \cdot \frac{5 \alpha}{3}\) = 14
⇒ 2α² + 5α(9 – \(\frac{5 \alpha}{3}\)) = 42
⇒ 2α² + 5α \(\frac{(27-5 \alpha)}{3}\) = 42
⇒ 6α² + 135α – 25α² = 126
⇒ 19α² – 135α + 126 = 0
⇒ 19α² – 114α – 21α + 126 = 0
⇒ 19α(α – 6) – 21(α – 6) = 0
⇒ (19α – 21)(α – 6) = 0
⇒ 19α – 21 = 0 or α – 6 = 0
⇒ α = \(\frac{21}{19}\) or α = 6
Case (i): α = 6
β = \(\frac{2 \alpha}{3}\)
= \(\frac{2}{3}\) × 6
= 4
γ = 9 – \(\frac{5 \alpha}{3}\)
= 9 – \(\frac{5}{3}\) × 6
= 9 – 10
= -1
α = 6, β = 4, γ = -1 satisfy αβγ = -24
∴ The roots are 6, 4, -1

Case (ii): α = \(\frac{21}{19}\)
β = \(\frac{2}{3} \times \frac{21}{19}=\frac{14}{19}\)
γ = 9 – \(\frac{5 \alpha}{3}\)
= 9 – \(\frac{5}{3} \cdot \frac{21}{19}\)
= \(\frac{136}{19}\)
These values do not satisfy αβγ= -24
∴ The roots are 6, 4, -1.

Question 4.
Solve the following equations, given that the roots of each are in A.P.
(i) 8x³ – 36x² – 18x + 81 = 0
Solution:
Given the roots of 8x³ – 36x² – 18x + 81 = 0 are in A.P.
Let the roots be a – d, a, a + d
Sum of the roots = \(\frac{36}{8}\)
⇒ a – d + a + a + d = \(\frac{9}{2}\)
⇒ 3a = \(\frac{9}{2}\)
⇒ a = \(\frac{3}{2}\)
∴ (x – \(\frac{3}{2}\)) is a factor of 8x³ – 36x² – 18x + 81 = 0

⇒ 8x² – 24x – 54 = 0
⇒ 4x² – 12x – 27 = 0
⇒ 4x² – 18x + 6x – 27 = 0
⇒ 2x(2x – 9) + 3(2x – 9) = 0
⇒ (2x + 3) (2x – 9) = 0
⇒ x = \(-\frac{3}{2}, \frac{9}{2}\)
∴ The roots are \(-\frac{3}{2}, \frac{3}{2}, \frac{9}{2}\)

(ii) x³ – 3x² – 6x + 8 = 0
Solution:
The roots of x³ – 3x² – 6x + 8 = 0 are in A.P
Suppose a – d, a, a + d be the roots
Sum = a – d + a + a + d = 3
⇒ 3a = 3
⇒ a = 1
∴ (x – 1) is a factor of x³ – 3x² – 6x + 8 = 0

⇒ x² – 2x – 8 = 0
⇒ x² – 4x + 2x – 8 = 0
⇒ x(x – 4)+ 2(x – 4) = 0
⇒ (x – 4) (x + 2) = 0
⇒ x = 4, -2
∴ The roots are -2, 1, 4

Question 5.
Solve the following equations, given that the roots of each are in G.P.
(i) 3x³ – 26x² + 52x – 24 = 0
Solution:
Given equation is 3x³ – 26x² + 52x – 24 = 0
The roots are in G.P.
Suppose \(\frac{a}{r}\), a, ar are the roots.
Product = \(\frac{a}{r}\) . a . ar = \(-\left(-\frac{24}{3}\right)\)
⇒ a³ = 8
⇒ a = 2
∴ (x – 2) is a factor of 3x³ – 26x² + 52x – 24

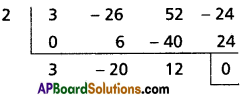
Hint: 3 × 12 = 3 ×6 × 2 = (-18)(-2)
⇒ 3x² – 20x + 12 = 0
⇒ 3x² – 18x – 2x + 12 = 0
⇒ 3x(x – 6) – 2(x – 6) = 0
⇒ (3x – 2) (x – 6) = 0
⇒ x = \(\frac{2}{3}\), 6
∴ The roots are \(\frac{2}{3}\), 2, 6.

(ii) 54x³ – 39x² – 26x + 16 = 0
Solution:
Given equation is 54x³ – 39x² – 26x + 16 = 0
The roots are in G.P.
Suppose \(\frac{a}{r}\), a, ar be the roots.
Product = \(\frac{a}{r}\) . a . ar = \(-\frac{16}{54}\)

Hint: 18 × 8 = 9 × 2 × 8 = (-9) (-16)
⇒ 54x² – 75x + 24 = 0
⇒ 18x² – 25x + 8 = 0
⇒ 18x² – 9x – 16x + 8 = 0
⇒ 9x(2x – 1) – 8(2x- 1) = 0
⇒ (9x – 8) (2x – 1) = 0
⇒ x = \(\frac{8}{9}, \frac{1}{2}\)
∴ The roots are \(\frac{8}{9},-\frac{2}{3}, \frac{1}{2}\)

Question 6.
Solve the following equations, given that the roots of each are in H.P.
(i) 6x³ – 11x² + 6x – 1 = 0
Solution:
Given equation is 6x³ – 11x² + 6x – 1 = 0 …….(1)
Put y = \(\frac{1}{x}\) so that \(\frac{6}{\mathrm{y}^{3}}-\frac{11}{\mathrm{y}^{2}}+\frac{6}{\mathrm{y}}-1\) = 0
⇒ 6 – 11y + 6y² – y³ = 0
⇒ y³ – 6y² + 11y – 6 = 0 ………(2)
Roots of (1) are in H.P.
⇒ Roots of (2) are in A.P.
Let a – d, a, a + d be the roots of (2)
Sum = a – d + a + a + d = 6
⇒ 3a = 6
⇒ a = 2
Product = a(a² – d²) = 6
⇒ 2(4 – d²) = 6
⇒ 4 – d² = 3
⇒ d² = 1
⇒ d = 1
a – d = 2 – 1 = 1,
a = 2
a + d = 2 + 1 = 3
The roots of (2) are 1, 2, 3
The roots of (1) are 1, \(\frac{1}{2}\), \(\frac{1}{3}\)

(ii) 15x³ – 23x² + 9x – 1 = 0
Solution:
Given equation is 15x³ – 23x² + 9x – 1 = 0 …….(1)
Put y = \(\frac{1}{x}\) so that \(\frac{15}{y^{3}}-\frac{23}{y^{2}}+\frac{9}{y}-1\) = 0
⇒ 15 – 23y + 9y² – y³ = 0
⇒ y³ – 9y² + 23y – 15 = 0 ………(2)
Roots of (1) are in H.P. So that roots of (2) are in A.P.
Let a – d, a, a + d be the roots of (2)
Sum = a – d + a + a + d = 9
⇒ 3a = 9
⇒ a = 3
Product = a(a² – d²) = 15
⇒ 3(9 – d²) = 15
⇒ 9 – d² = 5
⇒ d² = 4
⇒ d = 2
a – d = 3 – 2 = 1
a = 3
a + d = 3 + 2 = 5
Roots of (2) are 1, 3, 5
Hence roots of (1) are 1, \(\frac{1}{3}\), \(\frac{1}{5}\)

Question 7.
Solve the following equations, given that they have multiple roots.
(i) x⁴ – 6x³ + 13x² – 24x + 36 = 0
Solution:
(i) Let f(x) = x⁴ – 6x³ + 13x² – 24x + 36
⇒ f'(x) = 4x³ – 18x² + 26x – 24
⇒ f'(3) = 4(27) – 18(9) + 26(3) – 24
⇒ f'(3) = 108 – 162 + 78 – 24
⇒ f'(3) = 0
f(3) = 81 – 162 + 117 – 72 + 36 = 0
Hint: Choose the value of x from the factors of the G.C.D of constant terms in f(x) and f'(x).
∴ x – 3 is a factor of f'(x) and f(x)
∴ 3 is the repeated foot of f(x)

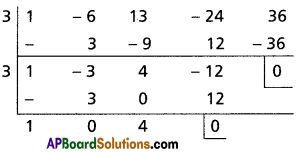
x² + 4 = 0
⇒ x = ±2i
∴ The roots of the given equation are 3, 3, ±2i

(ii) 3x⁴ + 16x³ + 24x² – 16 = 0
Solution:
Let f(x) = 3x⁴ + 16x³ + 24x² – 16
f(x) = 12x³ + 48x² + 48x
= 12x(x² + 4x + 4)
= 12x (x + 2)²
f'(-2) = 0
f(-2) = 3(16) + 16(-8) + 24(4) – 16 = 0
∴ x + 2 is a factor of f'(x) and f(x)
∴ -2 is a multiple root of f(x) = 0

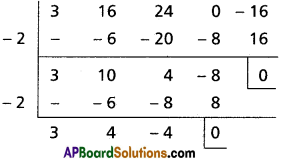
3x² + 4x – 4 = 0
⇒ 3x² + 6x – 2x – 4 = 0
⇒ 3x(x + 2) – 2(x + 2) = 0
⇒ (x + 2) (3x – 2) = 0
⇒ x = -2, \(\frac{2}{3}\)
∴ The roots of the given equation are -2, -2, -2, \(\frac{2}{3}\)

III.

Question 1.
Solve x⁴ + x³ – 16x² – 4x + 48 = 0, given that the product of two of the roots is 6.
Solution:
Suppose α, β, γ, δ are the roots of
x⁴ + x³ – 16x² – 4x + 48 = 0 ………..(1)
Sum of the roots = -1
⇒ α + β + γ + δ = -1
and Product of the roots = αβγδ = 48
∵ Product of two roots is 6
Let αβ = 6
From (1), γδ = \(\frac{48}{\alpha \beta}=\frac{48}{6}\) = 8
Let α + β = p and γ + δ = q
The equation having roots α, β is x² – (α + β) x + αβ = 0
⇒ x² – px + 6 = 0 ………..(2)
The equation having the roots γ, δ is x² – (γ + δ) x + γδ = 0
⇒ x² – qx + 8 = 0 ……….(3)
∴ From (1), (2) and (3)
x⁴ + x³ – 16x² – 4x + 48 = (x² – px + 6) (x² – qx + 8)
= x⁴ – (p + q) x³ + (pq + 14) x² – (8p + 86q) x + 48
Comparing the like terms,
p + q = -1
8p + 6q = 4 ⇒ 4p + 3q = 2
Solving, q = -6
∴ p = -1 + 6 = 5
Substitute the value of p in eq. (2),
x² – 5x + 6 = 0 ⇒ x = 2, 3
Substitute/the value of q in eq. (3),
x² + 6x + 8 = 0 ⇒ x = -2, – 4
∴ The roots of the given equation are -4, -2, 2, 3

Question 2.
Solve 8x⁴ – 2x³ – 27x² + 6x + 9 = 0 given that two roots have the same absolute value, but are opposite in signs.
Solution:
Suppose α, β, γ, δ are the roots of the equation
8x⁴ – 2x³ – 27x² + 6x + 9 = 0
⇒ \(x^{4}-\frac{1}{4} x^{3}-\frac{27}{8} x^{2}+\frac{3}{4} x+\frac{9}{8}=0\) …………(1)
Sum of the roots = α + β + γ + δ = \(\frac{1}{4}\) and
Product of the roots = αβγδ = \(\frac{9}{8}\)
Given β = -α
⇒ α + β = 0
∴ 0 + γ + δ = \(\frac{1}{4}\)
⇒ γ + δ = \(\frac{1}{4}\)
Let αβ = p, γδ = q, so that pq = \(\frac{9}{8}\)
The equation having the roots α, β is x² – (α + β)x + αβ = 0
⇒ x² + p = 0 ……….(2)
The equation having the roots γ, δ is x² – (γ + δ)x + γδ = 0
⇒ x² – \(\frac{1}{4}\) x + q = 0 ……..(3)
From (1), (2) and (3)
\(x^{4}-\frac{1}{4} x^{3}-\frac{27}{8} x^{2}+\frac{3}{4} x+\frac{9}{8}\) = (x² + p) \(\left(x^{2}-\frac{1}{4} x+q\right)\)
= \(x^{4}-\frac{1}{4} x^{3}+(p+q) x^{2}-\frac{p}{4} x+p q\)
Comparing the coefficients of x and constants
\(\frac{-p}{4}=\frac{3}{4}\) ⇒ p = -3
pq = \(\frac{9}{8}\)
⇒ q = \(\frac{9}{8} \times \frac{-1}{3}=\frac{-3}{8}\)
Substitute the value of p in eq. (2),
x² – 3 = 0 ⇒ x = ±√3
Substitute the value of q in eq. (3),
\(x^{2}-\frac{1}{4} x-\frac{3}{8}=0\)
⇒ 8x² – 2x – 3 = 0
⇒ (2x + 1) (4x – 3) = 6
⇒ x = \(-\frac{1}{2}, \frac{3}{4}\)
∴ The roots of the given equation are -√3, \(-\frac{1}{2}, \frac{3}{4}\), √3

Question 3.
Solve 18x³ + 81x² + 121x + 60 = 0 given that one root is equal to half the sum of the remaining roots.
Solution:
Suppose α, β, γ are the roots of 18x³ + 81x² + 121x + 60 = 0
sum = α + β + γ = \(\frac{-81}{18}=\frac{-9}{2}\) ……….(1)
αβ + βγ + γα = \(\frac{121}{18}\) …………(2)
αβγ = \(\frac{-60}{18}=\frac{-10}{3}\) ………(3)
∵ One root is equal to half of the sum of the remaining two,
Let α = \(\frac{1}{2}\) (β + γ)
Substitute in (1)

Question 4.
Find the condition in order that the equation ax⁴ + 4bx³ + 6cx² + 4dx + e = 0 may have a pair of equal roots.
Solution:
Let α, α, β, β are the roots of the equation.
ax⁴ + 4bx³ + 6cx² + 4dx + e = 0
⇒ \(x^{4}+\frac{4 b}{a} x^{2}+\frac{6 c}{a} x^{2}+\frac{4 d}{a} x+\frac{e}{a}=0\)
Sum of the roots, 2(α + β) = \(-\frac{4 b}{a}\)
⇒ α + β = \(-\frac{2 b}{a}\)
⇒ αβ = k (say)
Equation having roots α, β is x² – (α + β) x + αβ = 0

Question 5.
(i) Show that x⁵ – 5x³ + 5x² – 1 = 0 has three equal roots and find this root.
Solution:
Let f(x) = x⁵ – 5x³ + 5x² – 1
f'(x) = 5x⁴ – 15x² + 10x = 5x(x³ – 3x + 2)
f'(1) = 5(1) (1 – 3 + 2) = 0
f(1) = 1 – 5 + 5 – 1 = 0
x – 1 is a factor of f'(x) and f(x)
∴ 1 is a repeated root of f(x).

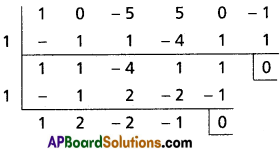
x³ + 2x² – 2x – 1 = 0
⇒ 1 is a root of the above equation (∵ sum of the coefficients is zero)
∴ 1 is the required root.

(ii) Find the repeated roots of x⁵ – 3x⁴ – 5x³ + 27x² – 32x + 12 = 0
Solution:
Let f(x) = x⁵ – 3x⁴ – 5x³ + 27x² – 32x + 12
f'(x) = 5x⁴ – 12x³ – 15x² + 54x – 32
f'(2) = 5(2)⁴ – 12(2)³ – 15(2)² + 54(2) – 32
= 80 – 96 – 60 + 108 – 32
= 0
f(2) = (2)⁵ – 3(2)⁴ – 5(2)³ + 27(2)² – 32(2) + 12
= 32 – 48 – 40 + 108 – 64 + 12
= 152 – 152
= 0
∴ x – 2 is a common factor of f'(x) and f(x)
2 is a multiple root of f(x) = 0

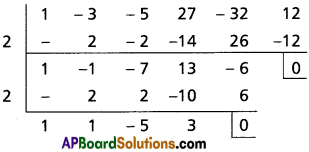
Let g(x) = x³ + x² – 5x + 3
g'(x) = 3x² + 2x – 5 = (3x + 5) (x – 1)
g(1) = 1 + 1 – 5 + 3 = 0
∴ x – 1 is a common factor of g'(x) and g(x)
∴ 1 is a multiple root of g(x) = 0

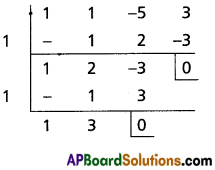
x + 3 = 0 ⇒ x = -3
∴ The roots are 2, 2, 1, 1, -3

Question 6.
Solve the equation 8x³ – 20x² + 6x + 9 = 0 given that the equation has multiple roots.
Solution:
Let f(x) = 8x³ – 20x² + 6x + 9
f'(x) = 24x² – 40x + 6
= 2 (12x² – 20x + 3)
= 2[12x² – 18x – 2x + 3]
= 2[6x(2x – 3) – 1(2x – 3)]
= 2(2x – 3) (6x – 1)
f'(x) = 0
⇒ x = \(\frac{3}{2}\), x = \(\frac{1}{6}\)
\(f\left(\frac{3}{2}\right)=8\left(\frac{3}{2}\right)^{3}-20\left(\frac{3}{2}\right)^{2}+6\left(\frac{3}{2}\right)+9\)
= 27 – 45 + 9 + 9
= 0
Hence x – \(\frac{3}{2}\) is a factor of f(x) and f'(x)
∴ \(\frac{3}{2}\) is a multiple root of f(x) = 0

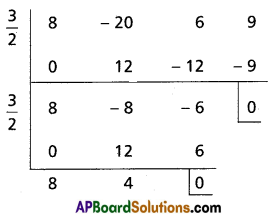
8x – 4 = 0
⇒ x = \(\frac{4}{8}=\frac{1}{2}\)
∴ The roots of the equation f(x) = 0 are \(\frac{3}{2}, \frac{3}{2}, \frac{1}{2}\)

Practicing the Intermediate 2nd Year Maths 2A Textbook Solutions Inter 2nd Year Maths 2A Theory of Equations Solutions Exercise 4(a) will help students to clear their doubts quickly.

Intermediate 2nd Year Maths 2A Theory of Equations Solutions Exercise 4(a)

I.

Question 1.
Form polynomial equations of the lowest degree, with roots as given below.
(i) 1, -1, 3
Solution:
Equation having roots α, β, γ is (x – α) (x – β) (x – γ) = 0
Sol. Required equation is (x – 1) (x + 1) (x – 3) = 0
⇒ (x² – 1) (x – 3) = 0
⇒ x³ – 3x² – x + 3 = 0

(ii) 1 ± 2i, 4, 2
Solution:
In an equation, imaginary roots occur in conjugate pairs.
Equation having roots α, β, γ, δ is (x – α) (x – β) (x – γ) (x – δ) = 0
Required equation is [x – (1 + 2i)] [x – (1 – 2i)] (x – 4) (x – 2) = 0
(x – (1 + 2i)] [x – (1 – 2i)] = [(x – 1) – 2i] [(x – 1) + 2i]
= (x – 1)² – 4i²
= (x – 1)² + 4
= x² – 2x + 1 + 4
= x² – 2x + 5
(x – 4) (x – 2) = x² – 4x – 2x + 8 = x² – 6x + 8
Required equation (x² – 2x + 5) (x² – 6x + 8) = 0
⇒ x⁴ – 2x³ + 5x² – 6x³ + 12x² – 30x + 8x² – 16x + 40 = 0
⇒ x⁴ – 8x³ + 25x² – 46x + 40 = 0

(iii) 2 ± √3, 1 ± 2i
Solution:
Required equation is [x – (2 + √3)] [x – (2 – √3)] [x – (1 + 2i)] [ x – (1 – 2i)] = 0
[x – (2 + √3)] [x – (2 – √3)]
= [(x – 2) – √3] [(x – 2) + √3]
= (x – 2)² – 3
= x² – 4x + 4 – 3
= x² – 4x + 1
[x – (1 + 2i)] [x – (1 – 2i)] = [(x – 1) – 2i] [(x – 1) + 2i]
= (x – 1)² – 4i²
= x² – 2x + 1 + 4
= x² – 2x + 5
Substituting in (1), the required equation is
(x² – 4x + 1) (x² – 2x + 5) = 0
⇒ x⁴ – 4x³ + x² – 2x³ + 8x² – 2x + 5x² – 20x + 5 = 0
⇒ x⁴ – 6x³ + 14x² – 22x + 5 = 0

(iv) 0, 0, 2, 2, -2, -2
Solution:
Required equation is (x – 0) (x – 0) (x – 2) (x – 2) (x + 2) (x + 2) = 0
⇒ x² (x – 2)² (x + 2)² = 0
⇒ x² (x² – 4)² = 0
⇒ x² (x⁴ – 8x² + 16) = 0
⇒ x⁶ – 8x⁴ + 16x² = 0

(v) 1 ± √3, 2, 5
Solution:
Required equation is [x – (1 + √3)] [x – (1 – √3)][(x – 2) (x – 5)] = 0 ………(1)
[x – (1 + √3)] [x – (1 – √3)] = [(x – 1) – √3] [(x – 1) + √3]
= (x – 1)² – 3
= x² – 2x + 1 – 3
= x² – 2x – 2
(x – 2) (x – 5) = x² – 2x – 5x + 10 = x² – 7x + 10
Substituting in (1), the required equation is
(x² – 2x – 2) (x² – 7x + 10) = 0
⇒ x⁴ – 2x³ – 2x² – 7x³ + 14x² + 14x + 10x² – 20x – 20 = 0
⇒ x⁴ – 9x³ + 22x² – 6x – 20 = 0

(vi) 0, 1, \(-\frac{3}{2}\), \(-\frac{5}{2}\)
Solution:
Required equation is

Question 2.
If α, β, γ are the roots of 4x³ – 6x² + 7x + 3 = 0, then find the value of αβ + βγ + γα.
Solution:
α, β, γ are the roots of 4x³ – 6x² + 7x + 3 = 0
α + β + γ = \(-\frac{a_{1}}{a_{0}}=\frac{6}{4}\)
αβ + βγ + γα = \(\frac{a_{2}}{a_{0}}=\frac{7}{4}\)
αβγ = \(-\frac{a_{3}}{a_{0}}=-\frac{3}{4}\)
∴ αβ + βγ + γα = \(\frac{7}{4}\)

Question 3.
If 1, 1, α are the roots of x³ – 6x² + 9x – 4 = 0, then find α.
Solution:
1, 1, α are roots of x³ – 6x² + 9x – 4 = 0
Sum = 1 + 1 + α = 6
⇒ α = 6 – 2 = 4

Question 4.
If -1, 2 and α are the roots of 2x³ + x² – 7x – 6 = 0, then find α.
Solution:
-1, 2, α are roots of 2x³ + x² – 7x – 6 = 0
Sum = -1 + 2 + α = \(-\frac{1}{2}\)
⇒ α = \(-\frac{1}{2}\) – 1 = \(-\frac{3}{2}\)

Question 5.
If 1, -2 and 3 are roots of x³ – 2x² + ax + 6 = 0, then find a.
Solution:
1, -2 and 3 are roots of x³ – 2x² + ax + 6 = 0
⇒ 1(-2) + (-2)3 + 3 . 1 = a
⇒ a = -2 – 6 + 3 = -5

Question 6.
If the product of the roots of 4x³ + 16x² – 9x – a = 0 is 9, then find a.
Solution:
α, β, γ are the roots of 4x³ + 16x² – 9x – a = 0
αβγ = 9
⇒ \(\frac{a}{4}\) = 9
⇒ a = 36

Question 7.
Find the values of s₁, s₂, s₃, and s₄ for each of the following equations.
(i) x⁴ – 16x³ + 86x² – 176x + 105 = 0
(ii) 8x⁴ – 2x³ – 27x² + 6x + 9 = 0

Solution:
(i) Given equation is x⁴ – 16x³ + 86x² – 176x + 105 = 0
We know that

(ii) Equation is 8x⁴ – 2x³ – 27x² + 6x + 9 = 0

II.

Question 1.
If α, β and 1 are the roots of x³ – 2x² – 5x + 6 = 0, then find α and β.
Solution:
α, β and 1 are the roots of x³ – 2x² – 5x + 6 = 0
Sum = α + β + 1 = 2
⇒ α + β = 1
product = αβ = -6
(α – β)² = (α + β)² – 4αβ
= 1 + 24
= 25
α – β = 5, α + β = 1
Adding
2α = 6
⇒ α = 3
α + β = 1
⇒ β = 1 – α
= 1 – 3
= -2
∴ α = 3 and β = -2

Question 2.
If α, β and γ are the roots of x³ – 2x² + 3x – 4 = 0, then find
(i) Σα²β²
(ii) Σαβ(α + β)
Solution:
Since α, β, γ are the roots of x³ – 2x² + 3x – 4 = 0 then
α + β + γ = 2
αβ + βγ + γα = 3
αβγ = 4
(i) Σα²β² = α²β² + β²γ² + γ²α²
= (αβ + βγ + γα)² – 2αβγ(α + β + γ)
= 9 – 2 . 2 . 4
= 9 – 16
= -7

(ii) Σαβ(α + β) = α²β + β²γ + γ²α + αβ² + βγ² + γα²
= (αβ + βγ + γα) (α + β + γ) – 3αβγ
= 2 . 3 – 3 . 4
= 6 – 12
= -6

Question 3.
If α, β and γ are the roots of x³ + px² + qx + r = 0, then find the following.
(i) \(\sum \frac{1}{\alpha^{2} \beta^{2}}\)
(ii) \(\frac{\beta^{2}+\gamma^{2}}{\beta \gamma}+\frac{\gamma^{2}+\alpha^{2}}{\gamma \alpha}+\frac{\alpha^{2}+\beta^{2}}{\alpha \beta}\) or \(\Sigma \frac{\beta^{2}+\gamma^{2}}{\beta \gamma}\)
(iii) (β + γ – 3α) (γ + α – 3β) (α + β – 3γ)
(iv) Σα³β³
Solution:
α, β and γ are the roots of x³ + px² + qx + r = 0,
α + β + γ = -p
αβ + βγ + γα = q
αβγ = -r

(iii) (β + γ – 3α) (γ + α – 3β) (α + β – 3γ) = (α + β + γ – 4α) (α + β + γ – 4β) (α + β + γ – 4γ)
= (-p – 4α) (-p – 4β) (-p – 4γ)
= -(p + 4α) (p + 4β) (p + 4γ)
= -(p³ + 4p² (α + β + γ) + 16p (αβ + βγ + γα) + (64αβγ)
= -(p³ – 4p³ + 16pq – 64r)
= 3p³ – 16pq + 64r

(iv) Σα³β³ = α³β³ + β³γ³ + γ³α³
(αβ + βγ + γα)² = α²β² + β²γ² + γ²α² + 2αβγ (α + β + γ)
⇒ q² = α²β² + β²γ² + γ²α² + 2pr
⇒ α²β² + β²γ² + γ²α² = q² – 2pr
∴ α³β³ + β³γ³ + γ³α³ = (α²β² + β²γ² + γ²α²) (αβ + βγ + γα) – αβγ Σα²β
= (q² – 2pr) . q + r[(αβ + βγ + γα) (α + β + γ) – 3αβγ]
= q³ – 2pqr + r(-pq + 3r)
= q³ – 2pqr – pqr + 3r²
= q³ – 3pqr + 3r²

III.

Question 1.
If α, β, γ are the roots of x³ – 6x² + 11x – 6 = 0, then find the equation whose roots are α² + β², β² + γ², γ² + α².
Solution:
1st Method:
Let α, β, γ are the roots of the equation x³ – 6x² + 11x – 6 = 0
∴ α + β + γ = 6, αβ + βγ + γα = 11
Let y = α² + β² = α² + β² + γ² – γ²
⇒ y = (α + β + γ)² – 2(αβ + βγ + γα) – x²
⇒ y = 36 – 22 – x²
⇒ x² = 14 – y
⇒ x = \(\sqrt{14-y}\)
Substitute x = \(\sqrt{14-y}\) in x³ – 6x² + 11x – 6 = 0
⇒ (\(\sqrt{14-y}\))3 – 6(\(\sqrt{14-y}\))2 + 11(\(\sqrt{14-y}\)) – 6 = 0
⇒ (14 – y) \(\sqrt{14-y}\) – 6(14 – y) + 11 \(\sqrt{14-y}\) – 6 = 0
⇒ -6(14 – y + 1) = \(\sqrt{14-y}\) [-11 – 14 + y]
⇒ -6(15 – y) = (\(\sqrt{14-y}\)) (y – 25)
Squaring on both sides
i.e., [-6(15 – y)]² = [\(\sqrt{14-y}\)(y – 25)]²
⇒ 36(225 – 30y + y²) = (14 – y)(y² – 50y + 625)
⇒ 8100 – 1080y + 36y² = 14y² – 700y + 8750 – y³ + 50y² – 625y
⇒ 8100 – 1080y + 36y² = -y³ + 64y² – 1325y + 8750
⇒ y³ – 28y² + 245y – 650 = 0
∴ The required equation is x³ – 28x² + 245x – 650 = 0
2nd Method:
Let α, β, γ are the roots of x³ – 6x² + 11x – 6 = 0
It is an odd-degree reciprocal equation of class two.
∴ x – 1 is a factor of x³ – 6x² + 11x – 6

∴ x³ – 6x² + 11x – 6 = (x – 1) (x² – 5x + 6) = (x – 1) ( x – 2) (x – 3)
∴ The roots of x³ – 6x² + 11x – 6 = 0 are α = 1, β = 2, γ = 3
Now α² + β² = 1² + 2² = 5
β² + γ² = 2² + 3² = 13
γ² + α² = 3² + 1² = 10
Therefore the cubic equation with roots α² + β², β² + γ², γ² + α² is (x – 5) (x – 13) (x – 10) = 0
⇒ x³ – (5 + 13 + 10) x² + (65 + 130 + 50)x – 650 = 0
⇒ x³ – 28x² + 245x – 650 = 0

Question 2.
If α, β, γ are the roots of x³ – 7x + 6 = 0, then find the equation whose roots are (α – β)², (β – γ)², (γ – α)²
Solution:
1st Method:
Let α, β, γ are the roots of the equation x³ – 7x + 6 = 0 …….(1)
α + β + γ = 0, αβγ = -6
Let y = (α – β)² = (α + β)² – 4αβ
⇒ y = (-γ)² – 4(\(\frac{6}{\gamma}\))
⇒ y = γ² + \(\frac{24}{\gamma}\)
⇒ y = x² + \(\frac{24}{x}\)
⇒ xy = x³ + 24
⇒ xy = 7x – 6 + 24 [from (1)]
⇒ x(y – 7) = 18
⇒ x = \(\frac{18}{y-7}\)
Substituting x = \(\frac{18}{y-7}\) in x³ – 7x + 6 = 0
(\(\frac{18}{y-7}\))3 – 6(\(\frac{18}{y-7}\)) + 6 = 0
⇒ (18)³ – 7(18) (y – 7)² + 6(y – 7)³ = 0
⇒ 5832 – 126(y² – 14y + 49) + 6(y³ – 21y² + 147y – 343) = 0
⇒ 972 – 21(y² – 14y + 49) + (y³ – 21y² + 147y – 343) = 0
⇒ y³ – 42y² + 441y – 400 = 0
∴ The equation with roots (α – β)², (β – γ)², (γ – α)² is x³ – 42x² + 441x – 400 = 0
2nd Method:
α, β, γ are the roots of x³ – 7x + 6 = 0
By trial and error method x = 1 satisfies this equation.
∴ x – 1 is a factor of x³ – 7x + 6

∴ x³ – 7x + 6 = (x – 1) (x² + x – 6) = (x – 1)(x + 3)(x – 2)
∵ α, β, γ are the roots of x³ – 7x + 6 = 0
α = 1, β = -3, γ = 2,
Now (α – β)² = [1 – (-3)]² = (4)² = 16
(β – γ)² = [-3 – 2]² = 25
(γ – α)² = [2 – 1]² = 1
∴ The cubic equation whose roots are (α – β)², (β – γ)², (γ – α)² is (x – 16) (x – 25) (x – 1) = 0
⇒ x³ – (16 + 25 + 1) x² + (400 + 25 + 16)x – 400 = 0
⇒ x³ – 42x² + 441x – 400 = 0

Question 3.
If α, β, γ are the roots of x³ – 3ax + b = 0, prove that Σ(α – β) (α – γ) = 9a.
Solution:
α, β, γ are the roots of x³ – 3ax + b = 0
∴ α + β + γ = 0, αβ + βγ + γα = -3a, αβγ = -b
Σ(α – β) (α – γ) = Σ[α² – α(β + γ) + βγ]
= Σ[α² + α² + βγl
= 2(α² + β² + γ²) + (βγ + γα + αβ)
= 2(α + β + γ)² – 4(αβ + βγ + γα) + (αβ + βγ + γα)
= 0 – 4(-3a) + (-3a)
= 9a

Practicing the Intermediate 2nd Year Maths 2A Textbook Solutions Inter 2nd Year Maths 2A Quadratic Expressions Solutions Exercise 3(c) will help students to clear their doubts quickly.

Intermediate 2nd Year Maths 2A Quadratic Expressions Solutions Exercise 3(c)

I.

Question 1.
Solve the following inequations by the algebraic method.
(i) 15x² + 4x – 4 ≤ 0
Solution:
15x² + 4x – 4 ≤ 0
⇒ 15x² – 6x + 10x – 4 ≤ 0
⇒ 3x(5x – 2) + 2(5x – 2) ≤ 0
⇒ (3x + 2) (5x – 2) ≤ 0
Co-efficient of x² = 15 > 0,
Given Expression is ≤ 0
⇒ x lies between \(\frac{-2}{3}\) and \(\frac{2}{5}\)
i.e., \(\frac{-2}{3} \leq x \leq \frac{2}{5}\)

(ii) x² – 2x + 1 < 0
Solution:
x² – 2x + 1 < 0
⇒ (x – 1)² < 0
There is no real value of ‘x’ satisfying this inequality
Solution set = Φ (or) Solution does not exist.

(iii) 2 – 3x – 2x² ≥ 0
Solution:
-(2x² + 3x – 2) ≥ 0
⇒ -(2x² + 4x – x – 2) ≥ 0
⇒ -[2x(x + 2) – 1(x + 2)] ≥ 0
⇒ -(2x – 1) (x + 2) ≥ 0
Co-efficient of x² = -2 < 0,
The given expression is ≥ 0
⇒ x lies between -2 and \(\frac{1}{2}\)
i.e., -2 ≤ x ≤ \(\frac{1}{2}\)

(iv) x² – 4x – 21 ≥ 0
Solution:
x² – 4x – 21 ≥ 0
⇒ x² – 7x + 3x – 21 ≥ 0
⇒ x(x – 7) + 3(x – 7) ≥ 0
⇒ (x + 3) (x – 7) ≥ 0
Co-efficient of x² = 1 > 0,
The given expression is ≥ 0
x does not lie between -3 and 7
i.e., {x/x ∈ (-∞, -3] ∪ [7, ∞)}

II.

Question 1.
Solve the following inequations by graphical method.
(i) x² – 7x + 6 > 0
Solution:
f(x) = x² – 7x + 6

f(x) > 0 ⇒ y > 0
Solutions are given by x < 1 and x > 6

(ii) 4 – x² > 0
Solution:
Let f(x) = 4 – x²

f(x) > 0 ⇒ y > 0
Solution set = {x/-2 < x < 2}

(iii) 15x² + 4x – 4 < 0
Solution:
Let f(x) = 15x² + 4x – 4

f(x) ≤ 0 ⇒ y ≤ 0
Solution set = \(\left\{x / \frac{-2}{3} \leq x \leq \frac{2}{5}\right\}\)

(iv) x² – 4x – 21 ≥ 0
Solution:
Let f(x) = x² – 4x – 21

f(x) ≥ 0 ⇒ y ≥ 0
Solution set = {x/x ∈ (-∞, -3] ∪ [7, ∞)}

Question 2.
Solve the following inequations.
(i) \(\sqrt{3 x-8}\) < -2
Solution:
L.H.S. is positive and R.H.S. is negative.
∴ The given inequality holds for no real x.
Solution set = Φ (or) Solution does not exist.

(ii) \(\sqrt{-x^{2}+6 x-5}\) > 8 – 2x
Solution:
\(\sqrt{-x^{2}+6 x-5}\) > 8 – 2x
⇔ -x² + 6x – 5 > 0
and (i) 8 – 2x < 0 (or) (ii) 8 – 2x ≥ 0
We have -x² + 6x – 5 = -(x² – 6x + 5) = -(x – 1) (x – 5)
Hence -x² + 6x – 5 ≥ 0 ⇔ x ∈ [1, 5]
(i) -x² + 6x – 5 ≥ 0 and 8 – 2x < 0
⇔ x ∈ [1, 5] and x > 4
⇔ x ∈ [4, 5] ………(1)
(ii) -x² + 6x – 5 ≥ 0 and 8 – 2x ≥ 0
∵ \(\sqrt{\left(-x^{2}+6 x-5\right)}\) > 8 – 2x
⇔ -x² + 6x – 5 > (8 – 2x)² and 8 – 2x ≥ 0
⇔ -x² + 6x – 5 > 64 + 4x² – 32x and x ≤ 4
⇔ -5x² + 38x – 69 > 0 and x ≤ 4
⇔ 5x² – 38x + 69 < 0 and x ≤ 4
⇔ 5x² – 15x – 23x + 69 < 0 and x ≤ 4
⇔ (5x – 23)(x – 3) < 0 and x ≤ 4
⇔ x ∈ (3, \(\frac{23}{5}\)) and x ≤ 4
⇔ x ∈ (3, \(\frac{23}{5}\)) ∩ (-∞, 4)
⇔ x ∈ (3, 4)
Hence the solution set of the given equation is x ∈ (4, 5) ∪ (3, 4)
⇒ x ∈ (3, 5) (or) 3 < x ≤ 5.

Practicing the Intermediate 2nd Year Maths 2A Textbook Solutions Inter 2nd Year Maths 2A Quadratic Expressions Solutions Exercise 3(b) will help students to clear their doubts quickly.

Intermediate 2nd Year Maths 2A Quadratic Expressions Solutions Exercise 3(b)

I.

Question 1.
If the quadratic equations ax² + 2bx + c = 0 and ax² + 2cx + b = 0, (b ≠ c) have a common root, then show that a + 4b + 4c = 0
Solution:
Let α be the common roots of the equations ax² + 2bx + c = 0 and ax² + 2cx + b = 0
aα² + 2bα + c = 0
aα² + 2cα + b = 0
on Subtracting,
2α(b – c) + c – b = 0
2α(b – c) = b – c
2α = 1 (b ≠ c)
α = \(\frac{1}{2}\)
Substitute α = \(\frac{1}{2}\) in ax² + 2bx + c = 0 is
\(a\left(\frac{1}{4}\right)+2 b \frac{1}{2}+c=0\)
⇒ a + 4b + 4c = 0
∴ a + 4b + 4c = 0

Question 2.
If x² – 6x + 5 = 0 and x² – 12x + p = 0 have a common root, then find p.
Solution:
Given x² – 6x + 5 = 0, x² – 12x + p = 0 have a common root.
If α is the common root then
α² – 6α + 5 = 0, α² – 12α + p = 0
α² – 6α + 5 = 0
⇒ (α – 1) (α – 5) = 0
⇒ α = 1 or 5
If α = 1 then α² – 12α + p = 0
⇒ 1 – 12 + p = 0
⇒ p = 11
If α = 5 then α² – 12α + p = 0
⇒ 25 – 60 + p = 0
⇒ p = 35
∴ p = 11 or 35

Question 3.
If x² – 6x + 5 = 0 and x² – 3ax + 35 = 0 have a common root, then find a.
Solution:
The roots of the equation x² – 6x + 5 = 0 are
(x – 1) (x – 5) = 0
⇒ x = 1, x = 5
Case (i): x = 1 is a common root then it is also root for the equation x² – 3ax + 35 = 0
⇒ 1 – 3a(1) + 35 = 0
⇒ a = 12
Case (ii): x = 5 is a common root then
(5)² – 3a(5) + 35 = 0
⇒ 60 – 15a = 0
⇒ a = 4
∴ a = 12 (or) a = 4

Question 4.
If the equation x² + ax + b = 0 and x² + cx + d = 0 have a common root and the first equation has equal roots, then prove that 2(b + d) = ac.
Solution:
Let α be the common root.
∴ x² + ax + b = 0 has equal roots.
Its roots are α, α
α + α = -a
⇒ α = \(-\frac{a}{2}\)
α . α = b
⇒ α² = b
∴ α is a root of x² + cx + d = 0
⇒ α² + cα + d = 0
⇒ b + c(\(-\frac{a}{2}\)) + d = 0
⇒ 2(b + d) = ac

Question 5.
Discuss the signs of the following quadratic expressions when x is real.
(i) x² – 5x + 4
Solution:
x² – 5x + 4 = (x – 1) (x – 4)
a = 1 > 0
The expression x² – 5x + 2 is positive if x < 1 or x > 4 and is negative if 1 < x < 4

(ii) x² – x + 3
Solution:
∆ = b² – 4ac
= (-1)² – 4 (1) (3)
= 1 – 12
= -11 < 0
a = 1 > 0, ∆ < 0
⇒ The given expression is positive for all real x.

Question 6.
For what values of x, the following expressions are positive?
(i) x² – 5x + 6
Solution:
x² – 5x + 6 = (x – 2) (x – 3)
Roots of x² – 5x + 6 = 0 are 2, 3 which are real.
The expression x² – 5x + 6 is positive if x < 2 or x > 3
∴ a = 1 > 0

(ii) 3x² + 4x + 4
Solution:
Here a = 3, b = 4, c = 4
∆ = b² – 4ac
= 16 – 48
= -32 < 0
∴ 3x² + 4x + 4 is positive ∀ x ∈ R
∴ a = 3 > 0 and ∆ < 0
ax² + bx + c and ‘a’ have same sign ∀ x ∈ R, if ∆ < 0

(iii) 4x – 5x² + 2
Solution:
Roots of 4x – 5x² + 2 = 0 are \(\frac{-4 \pm \sqrt{16+40}}{-10}\)
i.e., \(\frac{2 \pm \sqrt{14}}{5}\) which is real
∴ The expression 4x – 5x² + 2 is positive when
\(\frac{2-\sqrt{14}}{5}<x<\frac{2+\sqrt{14}}{5}\) [∵ a = -5 < 0]

(iv) x² – 5x + 14
Solution:
Here a = 1, b = -5, c = 14
∆ = b² – 4ac
= 25 – 56
= -31 < 0
∴ ∆ < 0 ∵ a = 1 > 0 and ∆ < 0
⇒ x² – 5x + 14 is positive ∀ x ∈ R.

Question 7.
For what values of x, the following expressions are negative?
(i) x² – 7x + 10
Solution:
x² – 7x + 10 = (x – 2)(x – 5)
Roots of x² – 7x + 10 = 0 are 2, 5 which are real.
∴ The expression x² – 7x + 10 is negative if 2 < x < 5, ∵ a = 1 > 0

(ii) 15 + 4x – 3x²
Solution:
The roots of 15 + 4x – 3x² = 0 are \(\frac{-4 \pm \sqrt{16+180}}{-6}\)
i.e., \(\frac{-5}{3}\), 3
∴ The expression 15 + 4x – 3x² is negative if
-5x < \(\frac{-5}{3}\) or x > 3, ∵ a = -3 < 0

(iii) 2x² + 5x – 3
Solution:
The roots of 2x² + 5x – 3 = 0 are \(\frac{-5 \pm \sqrt{25+24}}{4}\)
i.e., -3, \(\frac{1}{2}\)
∴ The expression 2x² + 5x – 3 is negative if -3 < x < \(\frac{1}{2}\), ∵ a = 2 > 0

(iv) x² – 5x – 6
Solution:
x² – 5x – 6 = (x – 6) (x + 1)
Roots of x² – 5x – 6 = 0 are -1, 6 which are real.
∴ The expression x² – 5x – 6 is negative if -1 < x < 6, ∵ a = 1 > 0

Question 8.
Find the changes in the sign of the following expressions and find their extreme values.
Hint: Let α, β are the roots of ax² + bx + c = 0 and α < β
(1) If x < α or x > β, ax² + bx + c and ‘a’ have same sign.
(2) If α < x < β, ax² + bx + c and ‘a’ have opposite sign.

(i) x² – 5x + 6
Solution:
x² – 5x + 6 = (x – 2) (x – 3)
(1) If 2 < x < 3, the sign of x² – 5x + 6 is negative, ∵ a = 1 > 0
(2) If x < 2 or x > 3, the sign of x² – 5x + 6 is positive, ∵ a = 1 > 0
Since a > 0, the minimum value of x² – 5x + 6 is \(\frac{4 a c-b^{2}}{4 a}\)
= \(\frac{4(1)(6)-(-5)^{2}}{4(1)}\)
= \(\frac{24-25}{4}\)
= \(-\frac{1}{4}\)
Hence the extreme value of the expression x² – 5x + 6 is \(-\frac{1}{4}\)

(ii) 15 + 4x – 3x²
Solution:
15 + 4x – 3x² = 15 + 9x – 5x – 3x²
= 3(5 + 3x) – x(5 + 3x)
= (3 – x) (5 + 3x)
(1) If \(-\frac{5}{3}\) < x < 3 the sign of 15 + 4x – 3x² is positive, ∵ a = -3 < 0
(2) If x < \(-\frac{5}{3}\) or x > 3, the sign of 15 + 4x – 3x² is negative, ∵ a = -3 < 0
Since a < 0, the maximum value of 15 + 4x – 3x² is \(\frac{4 a c-b^{2}}{4 a}\)
= \(\frac{4(-3)(15)-16}{4(-3)}\)
= \(\frac{49}{3}\)
Hence the extreme value of the expression 15 + 4x – 3x² is \(\frac{49}{3}\)

Question 9.
Find the maximum or minimum of the following expressions as x varies over R.
(i) x² – x + 7
Solution:
a = 1 > 0,
minimum value = \(\frac{4 a c-b^{2}}{4 a}\)
= \(\frac{28-1}{4}\)
= \(\frac{27}{4}\)

(ii) 12x – x² – 32
Solution:
a = -1 < 0,
maximum value = \(\frac{4 a c-b^{2}}{4 a}\)
= \(\frac{128-144}{-4}\)
= 4

(iii) 2x + 5 – 3x²
Solution:
a = -3 < 0,
maximum value = \(\frac{4 a c-b^{2}}{4 a}\)
= \(\frac{(4)(-3)(5)-(2)^{2}}{4 \times-3}\)
= \(\frac{16}{3}\)

(iv) ax² + bx + a
Solution:
If a < 0, then maximum value = \(\frac{4 a \cdot a-b^{2}}{4 a}\) = \(\frac{4 a^{2}-b^{2}}{4 a}\)
If a > 0, then minimum value = \(\frac{4 a \cdot a-b^{2}}{4 a}\) = \(\frac{4 a^{2}-b^{2}}{4 a}\)

II.

Question 1.
Determine the range of the following expressions.
(i) \(\frac{x^{2}+x+1}{x^{2}-x+1}\)
Solution:
Let y = \(\frac{x^{2}+x+1}{x^{2}-x+1}\)
⇒ x²y – xy + y = x² + x + 1
⇒ x²y – xy + y – x² – x – 1 = 0
⇒ x² (y – 1) – x(y + 1) + (y – 1) = 0
∴ x is real ⇒ b² – 4ac ≥ 0
⇒ (y + 1 )² – 4(y – 1 )² ≥ 0
⇒ (y + 1)² – (2y – 2)² ≥ 0
⇒ (y + 1 + 2y – 2) (y + 1 – 2y + 2) ≥ 0
⇒ (3y – 1) (-y + 3) ≥ 0
⇒ -(3y – 1) (y – 3) ≥ 0
a = Coeff of y² = -3 < 0
But The expression ≥ 0
⇒ y lies between \(\frac{1}{3}\) and 3
∴ The range of \(\frac{x^{2}+x+1}{x^{2}-x+1}\) is [\(\frac{1}{3}\), 0]

(ii) \(\frac{x+2}{2 x^{2}+3 x+6}\)
Solution:
Let y = \(\frac{x+2}{2 x^{2}+3 x+6}\)
Then 2yx² + 3yx + 6y = x + 2
⇒ 2yx² + (3y – 1)x + (6y – 2) = 0
∴ x is real ⇒ discriminant ≥ 0
⇒ (3y – 1)² – 4(2y)(6y – 2) ≥ 0
⇒ 9y² + 1 – 6y – 48y² + 16y ≥ 0
⇒ -39y² + 10y + 1 ≥ 0
⇒ 39y² – 10y – 1 < 0
⇒ 39y² – 13y + 3y – 1 < 0
⇒ 13y(3y – 1) + 1(3y – 1) ≤ 0
⇒ (3y – 1) (13y + 1) ≤ 0
∴ a = Coeff of y² = 39 > 0 and the exp ≤ 0
⇒ y lies between \(\frac{-1}{13}\) and \(\frac{1}{3}\)
∴ Range of \(\frac{x+2}{2 x^{2}+3 x+6}\) is \(\left[-\frac{1}{13}, \frac{1}{3}\right]\)

(iii) \(\frac{(x-1)(x+2)}{x+3}\)
Solution:
Let y = \(\frac{(x-1)(x+2)}{x+3}\)
⇒ yx + 3y = x² + x – 2
⇒ x² + (1 – y)x – 3y – 2 = 0
x ∈ R ⇒ (1 – y²) – 4(-3y – 2) ≥ 0
⇒ 1 + y² – 2y + 12y + 8 ≥ 0
⇒ y² + 10y + 9 ≥ 0
y² + 10y + 9 = 0
⇒ (y + 1) (y + 9) = 0
⇒ y = -1, -9
y² + 10y + 9 ≥ 0
∴ a = Coeff of y² = 1 > 0 and exp ≥ 0
⇒ y ≤ -9 or y ≥ -1
∴ Range = (-∞, -9] ∪ [-1, ∞)

(iv) \(\frac{2 x^{2}-6 x+5}{x^{2}-3 x+2}\)
Solution:
Let y = \(\frac{2 x^{2}-6 x+5}{x^{2}-3 x+2}\)
⇒ yx² – 3yx + 2y = 2x² – 6x + 5
⇒ (y – 2)x² + (6 – 3y)x + (2y – 5) = 0
x ∈ R ⇒ (6-3y)² – 4(y – 2) (2y – 5) ≥ 0
⇒ 36 + 9y² – 36y – 4(2y² – 9y + 10) ≥ 0
⇒ 36 + 9y² – 36y – 8y² + 36y – 40 ≥ 0
⇒ y² – 4 ≥ 0
y² – 4 = 0
⇒ y² = 4
⇒ y = ±2
y² – 4 ≥ 0
⇒ y ≤ -2 or y ≥ 2
⇒ y does not lie between -2, 2,
∵ y² Coeff is > 0 and exp is also ≥ 0
∴ Range of \(\frac{2 x^{2}-6 x+5}{x^{2}-3 x+2}\) is (-∞, -2] ∪ [2, ∞)

Question 2.
Prove that \(\frac{1}{3 x+1}+\frac{1}{x+1}-\frac{1}{(3 x+1)(x+1)}\) does not lie between 1 and 4, if x is real.
Solution:
Let y = \(\frac{1}{3 x+1}+\frac{1}{x+1}-\frac{1}{(3 x+1)(x+1)}\)
⇒ y = \(\frac{x+1+3 x+1-1}{(3 x+1)(x+1)}\)
⇒ y = \(\frac{4 x+1}{3 x^{2}+4 x+1}\)
⇒ 3yx² + 4yx + y = 4x + 1
⇒ 3yx² + (4y – 4)x + (y – 1) = 0
x ∈ R ⇒ (4y – 4)² – 4(3y)(y – 1) ≥ 0
⇒ 16y² + 16 – 32y – 12y² + 12y ≥ 0
⇒ 4y² – 20y + 16 ≥ 0
4y² – 20y + 16 = 0
⇒ y² – 5y + 4 = 0
⇒ (y – 1)(y – 4) = 0
⇒ y = 1, 4
4y² – 20y + 16 ≥ 0
⇒ y ≤ 1 or y ≥ 4
⇒ y does not lie between 1 and 4
Since y² Coeff is the and exp ≥ 0.

Question 3.
If x is real, prove that \(\frac{x}{x^{2}-5 x+9}\) lies between 1 and \(\frac{-1}{11}\).
Solution:
Let y = \(\frac{x}{x^{2}-5 x+9}\)
⇒ yx² + (-5y – 1)x + 9y = 0
x ∈ R ⇒ (5y – 1)² – 4y(9y) ≥ 0
⇒ 25y² + 1 + 10y – 36y² ≥ 0
⇒ -11y² + 10y + 1 ≥ 0 ……….(1)
-11y² + 10y + 1 = 0
⇒ -11y² + 11y – y + 1 = 0
⇒ 11y(-y + 1) + 1(-y + 1) = 0
⇒ (-y + 1) (11y + 1) = 0
⇒ y = 1, \(\frac{-1}{11}\)
-11y² + 10y + 1 ≥ 0
∴ y² Coeff is -ve, but the exp is ≥ 0 from (1)
⇒ \(\frac{-1}{11}\) ≤ y ≤ 1
⇒ y lies between 1 and \(\frac{-1}{11}\)

Question 4.
If the expression \(\frac{x-p}{x^{2}-3 x+2}\) takes all real value for x ∈ R, then find the bounts for p.
Solution:
Let y = \(\frac{x-p}{x^{2}-3 x+2}\), given y is real
Then yx² – 3yx + 2y = x – p
⇒ yx² + (-3y – 1)x + (2y + p) = 0
∵ x is real ⇒ (-3y – 1)² – 4y(2y + p) ≥ 0
⇒ 9y² + 6y + 1 – 8y² – 4py ≥ 0
⇒ y² + (6 – 4p)y + 1 ≥ 0
∵ y is real ⇒ y² + (6 – 4p)y + 1 ≥ 0
⇒ The roots are imaginary or real and equal
⇒ ∆ ≤ 0
⇒ (6 – 4p)² – 4 ≤ 0
⇒ 4(3 – 2p)² – 4 ≤ 0
⇒ (3 – 2p)² – 1 ≤ 0
⇒ 4p² – 12p + 8 ≤ 0
⇒ p² – 3p + 2 ≤ 0
⇒ (p – 1)(p – 2) ≤ 0
If p = 1 or p = 2 then \(\frac{x-p}{x^{2}-3 x+2}\) is not defined.
∴ 1 < p < 2

Question 5.
If c² ≠ ab and the roots of (c² – ab)x² – 2(a² – bc)x + (b² – ac) = 0 are equal, then show that a³ + b³ + c³ = 3abc or a = 0.
Solution:
Given equation is (c² – ab)x² – 2(a² – bc)x + (b² – ac) = 0
Discriminant = 4(a² – bc)² – 4(c² – ab) (b² – ac)
= 4[(a² – bc)² – (c² – ab) (b² – ac)]
= 4(a⁴ + b²c² – 2a²bc – b²c² + ac³ + ab³ – a²bc)
= 4(a⁴ + ab³ + ac³ – 3a²bc)
= 4a(a³ + b³ + c³ – 3abc)
The roots are equal ⇒ discriminant = 0
4a(a³ + b³ + c³ – 3abc) = 0
a = 0 or a³ + b³ + c³ – 3abc = 0
i.e., a = 0 or a³ + b³ + c³ = 3abc

Practicing the Intermediate 2nd Year Maths 2A Textbook Solutions Inter 2nd Year Maths 2A Quadratic Expressions Solutions Exercise 3(a) will help students to clear their doubts quickly.

Intermediate 2nd Year Maths 2A Quadratic Expressions Solutions Exercise 3(a)

I.

Question 1.
Find the roots of the following equations.
(i) x² – 7x + 12 = 0
Solution:
a = 1, b = -7, c = 12

∴ The roots are 4, 3

(ii) -x² + x + 2 = 0
Solution:
a = -1, b = 1, c = 2

∴ The roots are 2, -1

(iii) 2x² + 3x + 2 = 0
Solution:
a = 2, b = 3, c = 2

(iv) √3x² + 10x – 8√3 = 0
Solution:
a = √3 , b = 10, c = -8√3

∴ The roots are \(\frac{2}{\sqrt{3}}\), -4√3

(v) 6√5x² – 9x – 3√5 = 0
Solution:
a = 6√5 , b = -9, c = -3√5

∴ The roots are \(\frac{\sqrt{5}}{2},-\frac{1}{\sqrt{5}}\)

Question 2.
Form a quadratic equation whose roots are:
(i) 2, 5
Solution:
α + β = 2 + 5 = 7
αβ = 2 × 5 = 10
The required equation is x² – (α + β)x + αβ = 0
⇒ x² – 7x + 10 = 0

(ii) \(\frac{m}{n},-\frac{n}{m}\), (m ≠ 0, n ≠ 0)
Solution:

(iii) \(\frac{p-q}{p+q}, \frac{-p+q}{p-q}\), (p ≠ ±q)
Solution:

(iv) 7 ± 2√5
Solution:
α + β = 7 + 2√5 + 7 – 2√5 = 14
αβ = (7 + 2√5) (7 – 2√5)
= 49 – 20
= 29
The required equation is x² – (α + β)x + αβ = 0
⇒ x² – 14x + 29 = 0

(v) -3 ± 5i
Solution:
α + β = -3 + 5i – 3 – 5i = -6
αβ = (-3 + 5i) (-3 – 5i)
= 9 + 25
= 34
The required equation is x² – (α + β)x + αβ = 0
⇒ x² + 6x + 34 = 0

Question 3.
Find the nature of the roots of the following equation, without finding the roots.
(i) 2x² – 8x + 3 = 0
Solution:
a = 2, b = -8, c = 3
b² – 4ac = 64 – 24 = 40 > 0
∴ The roots are real and distinct.

(ii) 9x² – 30x + 25 = 0
Solution:
a = 9, b = -30, c = 25
b² – 4ac = 900 – 900 = 0
∴ The roots are rational and equal.

(iii) x² – 12x + 32 = 0
Solution:
a = 1, b = -12, c = 32
b² – 4ac = 144 – 128
= 16
= (4)²
= perfect square
∴ The roots are rational and distinct.

(iv) 2x² – 7x + 10 = 0
Solution:
a = 2, b = -7, c = 10
b² – 4ac = 49 – 80 = -31 < 0
∴ The roots are complex conjugate numbers.

Question 4.
If α, β are the roots of the equation ax² + bx + c = 0, find the values of the following expressions in terms of a, b, c.
(i) \(\frac{1}{\alpha}+\frac{1}{\beta}\)
(ii) \(\frac{1}{\alpha^{2}}+\frac{1}{\beta^{2}}\)
(iii) α⁴β⁷ + α⁷β⁴
(iv) \(\left(\frac{\alpha}{\beta}-\frac{\beta}{\alpha}\right)^{2}\), if c ≠ 0
(v) \(\frac{\alpha^{2}+\beta^{2}}{\alpha^{-2}+\beta^{-2}}\)
Solution:
α, β are the roots of the equation ax² + bx + c = 0
α + β = \(\frac{-b}{a}\), αβ = \(\frac{c}{a}\)

Question 5.
Find the values of m for which the following equations have equal roots.
(i) x² – 15 – m(2x – 8) = 0
Solution:
Given equation is x² – 15 – m(2x – 8) = 0
⇒ x² – 2mx + 8m – 15 = 0
a = 1, b = -2m, c = 8m – 15
b² – 4ac = (-2m)² – 4(1) (8m – 15)
= 4m² – 32m + 60
= 4(m² – 8m + 15)
= 4(m – 3) (m – 5)
If the equation ax² + bx + c = 0 has equal roots then its discriminant is zero.
∴ The roots are equal
⇒ b² – 4ac = 0
⇒ 4(m – 3) (m – 5) = 0
⇒ m – 3 = 0 or m – 5 = 0
⇒ m = 3 or 5

(ii) (m + 1)x² + 2(m + 3)x + (m + 8) = 0
Solution:
Given equation is (m + 1 )x² + 2(m + 3)x + (m + 8) = 0
a = m + 1, b = 2(m + 3), c = m + 8
b² – 4ac = [2(m + 3)]² – 4(m + 1) (m + 8)
= 4(m² + 6m + 9) – 4(m² + 8m + m + 8)
= 4m² + 24m + 36 – 4m² – 36m – 32
= -12m + 4
= -4(3m – 1)
∴ The roots are equal
⇒ b² – 4ac = 0
⇒ -4(3m – 1) = 0
⇒ 3m – 1 = 0
⇒ 3m = 1
⇒ m = \(\frac{1}{3}\)

(iii) x² + (m + 3)x + m + 6 = 0
Solution:
Given equation is x² + (m + 3)x + m + 6 = 0
a = 1, b = m + 3, c = m + 6
∴ The roots are equal
⇒ b² – 4ac = 0
⇒ (m + 3)² – 4(1) (m + 6) = 0
⇒ m² + 6m + 9 – 4m – 24 = 0
⇒ m² + 2m – 15 – 0
⇒ m² + 5m – 3m – 15 = 0
⇒ m(m + 5) – 3(m + 5) = 0
⇒ (m + 5) (m – 3) = 0
⇒ m = -5, 3

(iv) (3m + 1)x² + 2(m + 1)x + m = 0
Solution:
Given equation is (3m + 1)x² + 2(m + 1)x + m = 0
a = 3m + 1, b = 2(m + 1), c = m
b² – 4ac = 4(m + 1)² – 4m(3m + 1)
= 4[(m + 1)² – m(3m + 1)]
= 4(m² + 2m + 1 – 3m² – m)
= 4(-2m² + m + 1)
= -4(2m² – m – 1)
= -4(m – 1) (2m + 1)
∴ The roots are equal
⇒ discriminant = 0
⇒ b² – 4ac = 0
⇒ -4(m – 1) (2m + 1) = 0
⇒ m – 1 = 0 or 2m + 1 = 0
⇒ m = 1 or m = \(\frac{-1}{2}\)

(v) (2m + 1)x² + 2(m + 3)x + (m + 5) = 0
Solution:
Given equation is (2m + 1)x² + 2(m + 3)x + m + 5 = 0
a = 2m + 1, b = 2(m + 3), c = m + 5
∴ The roots are equal
⇒ b² – 4ac = 0
⇒ 4(m + 3)² – 4(2m + 1) (m + 5) = 0
⇒ 4(m² + 6m + 9 – 2m² – 10m – m – 5) = 0
⇒ -m² – 5m + 4 = 0
⇒ m² + 5m – 4 = 0
⇒ m = \(\frac{-5 \pm \sqrt{25+16}}{2}\)
⇒ m = \(\frac{-5 \pm \sqrt{41}}{2}\)

Question 6.
If α and β are the roots of x² + px + q = 0, form a quadratic equation whose roots are (α – β)² and (α + β)².
Solution:
∵ α, β are the roots of the equation x² + px + q = 0
α + β = -p, αβ = q
(α – β)² + (α + β)² = 2(α² + β²)
= 2[(α + β)² – 2αβ]
= 2[p² – 2q]
(α – β)² (α + β)² = [(α + β)² – 4αβ)] (α + β)²
= (p² – 4q) (p²)
∴ The required equation is x² – (sum of the roots) x + product of the roots = 0
∴ x² – 2(p² – 2q)x + p²(p² – 4q) = 0

Question 7.
If x² + bx + c = 0, x² + cx + b = 0 (b ≠ c) have a common root, then show that b + c + 1 = 0.
Solution:
If α is a common root of x² + bx + c = 0, x² + cx + b = 0 then
α² + bα + c = 0 ………..(1)
α² + cα + b = 0 ……….(2)
(1) – (2) ⇒ (b – c)α + (c – b) = 0
⇒ α – 1 = 0
⇒ α = 1
From (1), 1 + b + c = 0
Hence b + c + 1 = 0

Question 8.
Prove that the roots of (x – a) (x – b) = h² are always real.
Solution:
Given equation is (x – a) (x – b) = h²
x² – (a + b)x + (ab – h²) = 0
Discriminant = (a + b)² – 4(ab – h²)
= (a + b)² – 4ab + 4h²
= (a – b)² + (2h)² > 0
∴ The roots are real.

Question 9.
Find the condition that one root of the quadratic equation ax² + bx + c = 0 shall be n times the other, where n is a positive integer.
Solution:
Let the roots of the equation ax² + bx + c = 0 be α, nα

Question 10.
Find two consecutive positive even integers, the sum of whose squares is 340.
Solution:
Let the two consecutive positive even integers be 2λ, 2λ + 2
Sum of squares = 340
⇒ (2λ)² + (2λ + 2)² = 340
⇒ λ² + (λ + 1)² = 85
⇒ λ² + λ² + 2λ + 1 – 85 = 0
⇒ 2λ² + 2λ – 84 = 0
⇒ λ² + λ – 42 = 0
⇒ (λ + 7) (λ – 6) = 0
⇒ λ = 6, λ = -7
∵ Given numbers are positive λ = 6
∴ The two consecutive positive even integers are
2λ = 2(6) = 12 and 2λ + 2 = 12 + 2 = 14

II.

Question 1.
If x₁, x₂ are the roots of the quadratic equation ax² + bx + c = 0 and c ≠ 0, find the value of (ax₁ + b)^-2 + (ax₂ + b)^-2 terms of a, b, c.
Solution:
x₁, x₂ are the roots of the equation ax² + bx + c = 0

Question 2.
If α, β are the roots of the quadratic equation ax² + bx + c = 0, form a quadratic equation whose roots are α² + β² and α^-2 + β^-2.
Solution:
α, β are the roots of ax² + bx + c = 0, then

Question 3.
Solve the following equation:
2x⁴ + x³ – 11x² + x + 2 = 0
Solution:
2x⁴ + x³ – 11x² + x + 2 = 0
Dividing by x²

Substituting in (1)
2(a² – 2) + a – 11 = 0
⇒ 2a² – 4 + a – 11 = 0
⇒ 2a² + a – 15 = 0
⇒ (a + 3) (2a – 5) = 0
⇒ a + 3 = 0 or 2a – 5 = 0
⇒ a = -3 or 2a = 5
⇒ a = -3 or a = \(\frac{5}{2}\)

⇒ 2x² + 2 = 5x
⇒ 2x² – 5x + 2 = 0
⇒ (2x – 1) (x – 2) = 0
⇒ 2x – 1 = 0 or x – 2 = 0
⇒ x = \(\frac{1}{2}\), 2
∴ The roots are \(\frac{1}{2}\), 2, \(\frac{-3 \pm \sqrt{5}}{2}\)

Question 4.
Solve 3^1+x + 3^1-x = 10
Solution:
3^1+x + 3^1-x = 10
\(\text { 3. } 3^{x}+\frac{3}{3^{x}}=10\)
Put a = 3^x so that 3a + \(\frac{3}{a}\) = 10
⇒ 3a² + 3 = 10a
⇒ 3a² – 10a + 3 = 0
⇒ (a – 3) (3a – 1) = 0
⇒ a – 3 = 0 or 3a – 1 = 0
⇒ a = 3 or a = \(\frac{1}{3}\)
Case (i): a = 3
⇒ 3^x = 3¹
⇒ x = 1
Case (ii): a = \(\frac{1}{3}\)
⇒ 3^x = 3^-1
⇒ x = -1
∴ The roots are 1, -1

Question 5.
Solve 4^x-1 – 3 . 2^x-1 + 2 = 0
Solution:
4^x-1 – 3 . 2^x-1 + 2 = 0
Put a = 2^x-1 so that a² = (2^x-1)² = 4^x-1
∴ a² – 3a + 2 = 0
⇒ (a – 2) (a – 1) = 0
⇒ a – 2 = 0 or a – 1 = 0
⇒ a = 2 or 1
Case (i): a = 2
2^x-1 = 2¹
⇒ x – 1 = 1
⇒ x = 2
Case (ii): a = 1
2^x-1 = 2⁰
⇒ x – 1 = 0
⇒ x = 1
∴ The roots are 1, 2

Question 6.
\(\sqrt{\frac{x}{x-3}}+\sqrt{\frac{x-3}{x}}=\frac{5}{2}\), when x ≠ 0 and x ≠ 3
Solution:
\(\sqrt{\frac{x}{x-3}}+\sqrt{\frac{x-3}{x}}=\frac{5}{2}\)
Put a = \(\sqrt{\frac{x}{x-3}}\)
\(a+\frac{1}{a}=\frac{5}{2}\)
⇒ \(\frac{a^{2}+1}{a}=\frac{5}{2}\)
⇒ 2a² + 2 = 5a
⇒ 2a² – 5a + 2 = 0
⇒ (2a – 1) (a – 2) = 0
⇒ 2a – 1 = 0 or a – 2 = 0
⇒ a = \(\frac{1}{2}\) or 2
Case (i): a = 2
\(\sqrt{\frac{x}{x-3}}\) = 2
⇒ \(\frac{x}{x-3}\) = 4
⇒ x = 4x – 12
⇒ 3x = 12
⇒ x = 4
Case (ii): a = \(\frac{1}{2}\)
\(\sqrt{\frac{x}{x-3}}=\frac{1}{2}\)
⇒ \(\frac{x}{x-3}=\frac{1}{4}\)
⇒ 4x = x – 3
⇒ 3x = -3
⇒ x = -1
∴ The roots are -1, 4.

Question 7.
\(\sqrt{\frac{3 x}{x+1}}+\sqrt{\frac{x+1}{3 x}}=2\), when x ≠ 0 and x ≠ -1
Solution:
Put a = \(\sqrt{\frac{3 x}{x+1}}\)
\(a+\frac{1}{a}=2\)
⇒ \(\frac{a^{2}+1}{a}\) = 2
⇒ a² + 1 = 2a
⇒ a² – 2a + 1 = 0
⇒ (a – 1)² = 0
⇒ a – 1 = 0
⇒ a = 1, 1
∴ \(\sqrt{\frac{3 x}{x+1}}\) = 1
⇒ \(\frac{3 x}{x+1}\)
⇒ 3x = x + 1
⇒ 2x = 1
⇒ x = \(\frac{1}{2}\)
∴ The root is \(\frac{1}{2}\)

Question 8.
Solve \(2\left(x+\frac{1}{x}\right)^{2}-7\left(x+\frac{1}{x}\right)+5=0\), when x ≠ 0.
Solution:
\(2\left(x+\frac{1}{x}\right)^{2}-7\left(x+\frac{1}{x}\right)+5=0\)
Put a = x + \(\frac{1}{x}\)
⇒ 2a² – 7a + 5 = 0
⇒ (2a – 5)(a – 1) = 0
⇒ 2a – 5 = 0 or a -1 = 0
⇒ a = \(\frac{5}{2}\) or 1
Case (i): a = \(\frac{5}{2}\)
x + \(\frac{1}{x}\) = \(\frac{5}{2}\)
⇒ \(\frac{x^{2}+1}{x}=\frac{5}{2}\)
⇒ 2x² + 2 = 5x
⇒ 2x² – 5x + 2 = 0
⇒ (2x – 1) (x – 2) = 0
⇒ 2x – 1 = 0 or x – 2 = 0
⇒ x = \(\frac{1}{2}\) or 2
Case (ii): a = 1
\(x+\frac{1}{x}=1\)
⇒ \(\frac{x^{2}+1}{x}\)
⇒ x² + 1 = x
⇒ x² – x + 1 = 0
⇒ x = \(\frac{1 \pm \sqrt{1-4}}{2}=\frac{1 \pm \sqrt{3 i}}{2}\)
∴ The roots are \(\frac{1 \pm \sqrt{3 i}}{2}, \frac{1}{2}\), 2

Question 9.
Solve \(\left(x^{2}+\frac{1}{x^{2}}\right)-5\left(x+\frac{1}{x}\right)+6=0\), when x ≠ 0
Solution:
Put a = x + \(\frac{1}{x}\)
⇒ a² = \(\left(x+\frac{1}{x}\right)^{2}\)
⇒ a² = \(x^{2}+\frac{1}{x^{2}}+2\)
⇒ \(x^{2}+\frac{1}{x^{2}}\) = a² – 2
∴ a² – 2 – 5a + 6 = 0
⇒ a² – 5a + 4 = 0
⇒ (a – 1) (a – 4) = 0
⇒ a = 1 or 4
Case (i): a = 1
x + \(\frac{1}{x}\) = 1
⇒ \(\frac{x^{2}+1}{x}\) = 1
⇒ x² + 1 = x
⇒ x² – x + 1 = 0
⇒ x = \(\frac{1 \pm \sqrt{1-4}}{2}=\frac{1 \pm \sqrt{3 i}}{2}\)
Case (ii): a = 4
x + \(\frac{1}{x}\) = 4
⇒ \(\frac{x^{2}+1}{x}\) = 4
⇒ x² + 1 = 4x
⇒ x² – 4x + 1 = 0
⇒ x = \(\frac{4 \pm \sqrt{16-4}}{2}\)
⇒ x = \(\frac{4 \pm 2 \sqrt{3}}{2}\)
⇒ x = 2 ± √3
∴ The roots are 2 ± √3, \(\frac{1 \pm \sqrt{3 i}}{2}\)

Question 10.
Find a quadratic equation for which the sum of the roots is 7 and the sum of the squares of the roots is 25.
Solution:
Let α, β be the roots of quadratic equation
α + β = 7, α² + β² = 25
⇒ (α + β)² – 2αβ = 25
⇒ 49 – 25 = 2αβ
⇒ αβ = 12
The required equation is x² – (α + β)x + αβ = 0
⇒ x² – 7x + 12 = 0

Telangana & Andhra Pradesh BIEAP TS AP Intermediate Inter 2nd Year Study Material Textbook Solutions Guide PDF Free Download, Sakshi Education Intermediate 2nd Study Material in English Medium and Telugu Medium are part of AP Intermediate Study Material. The curriculum has been designed in such a way, to help them learn the different subjects and concepts in an interesting and easy manner. These AP Intermediate 2nd Year Textbook Solutions will prove to be useful study tools during exam preparation.

The AP Inter 2nd Year Syllabus has also been created to address the most important learning needs of the students. That being said, BIEAP Inter 2nd Year students can actually succeed in academics by making use of AP Inter 2nd Year Study Material Pdf. As such, they can also make use of AP Intermediate 2nd Year Previous Year Question Papers, which will further enable them to understand the actual exam paper in a clear manner.

AP Intermediate 2nd Year Study Material Pdf Download | Sr Inter 2nd Year Textbook Solutions

Here is AP Intermediate 2nd Year Study Material to help students prepare and ace the AP Intermediate 2nd year exams.

AP Inter 2nd Year Study Material Pdf

• Intermediate 2nd Year Maths 2A Textbook Solutions
• Intermediate 2nd Year Maths 2B Textbook Solutions
• AP Inter 2nd Year Physics Study Material
• AP Inter 2nd Year Chemistry Study Material
• AP Inter 2nd Year Botany Study Material
• AP Inter 2nd Year Zoology Study Material
• AP Inter 2nd Year Telugu Study Material
• AP Inter 2nd Year English Study Material
• AP Inter 2nd Year Sanskrit Study Material
• AP Inter 2nd Year Hindi Study Material
• AP Inter 2nd Year Civics Study Material
• AP Inter 2nd Year Commerce Study Material
• AP Inter 2nd Year Accountancy Study Material
• AP Inter 2nd Year Economics Study Material

AP Inter 2nd Year Important Questions

• Inter 2nd Year Maths 2A Important Questions
• Inter 2nd Year Maths 2B Important Questions
• AP Inter 2nd Year Physics Important Questions
• AP Inter 2nd Year Chemistry Important Questions
• AP Inter 2nd Year Botany Important Questions
• AP Inter 2nd Year Zoology Important Questions
• AP Inter 2nd Year Civics Important Questions
• AP Inter 2nd Year Commerce Important Questions
• AP Inter 2nd Year Accountancy Important Questions
• AP Inter 2nd Year Economics Important Questions

AP Inter 2nd Year Notes

• Inter 2nd Year Maths 2A Formulas
• Inter 2nd Year Maths 2B Formulas
• AP Inter 2nd Year Physics Notes
• AP Inter 2nd Year Chemistry Notes
• AP Inter 2nd Year Botany Notes
• AP Inter 2nd Year Zoology Notes
• AP Inter 2nd Year Civics Notes
• AP Inter 2nd Year Commerce Notes
• AP Inter 2nd Year Accountancy Notes
• AP Inter 2nd Year Economics Notes

We hope that these Telangana & Andhra Pradesh BIEAP TS AP Intermediate Inter 2nd Year Study Material Textbook Solutions Guide PDF Free Download in English Medium and Telugu Medium helps the student to come out successful with flying colors in this examination. This Sr Inter 2nd Year Study Material will help students to gain the right knowledge to tackle any type of questions that can be asked during the exams.

Students get through AP Inter 2nd Year Chemistry Important Questions Lesson 6(d) Group-18 Elements which are most likely to be asked in the exam.

AP Inter 2nd Year Chemistry Important Questions Lesson 6(d) Group-18 Elements

Very Short Answer Questions

Question 1.
List out the uses of Neon.
Answer:
Uses of Ne:

1. Ne is used in discharge tubes and fluorescent bulbs for advertisement display purposes.
2. ‘Ne’ – bulbs are used in botanical gardens and in greenhouses.

Question 2.
Write any two uses of argon.
Answer:
Uses of Ar:

1. ‘Ar’ is used to create inert atmosphere in high temperature metallurgical process.
2. ‘Ar’ is used in filling electric bulbs.

Question 3.
In modern diving apparatus, a mixture of He ánd O₂ is used – Why? (IPE 2016 (AP))
Answer:
In modem diving apparatus, a mixture of He and O₂ is used because He is very low soluble in blood.

Question 4.
Helium is heavier than hydrogen. Yet helium is used (instead of H₂) in filling balloons for meteorological observations – Why?
Answer:
‘He’ is a non—inflammable and light gas. Hence it is used in filling balloons for meterological observations.

Question 5.
How is XeO₃ prepared? (IPE May – 2015(AP), 2014)
Answer:
XeF₆ on hydrolysis produce XeO₃.
XeF₆ + 3H₂O → XeO₃ + 6HF

Question 6.
Give the preparation of
a) XeOF₄ and
b) XeO₂F₂. (TS Mar. 17; IPE 2014)
Answer:
Partial hydrolysis of XeF₆ gives oxy fluorides XeOF₄ and XeO₂F₂
XeF₆ + H₂O → XeOF₄ + 2HF
XeF₆ + 2H₂O → XeO₂F₂ + 4HF

Question 7.
Explain the structure of XeO₃. (TS Mar. 17; IPE 16, 15’ 14 (TS))
Answer:
Structure of XeO₃:

1. Central atom is Xe’.
2. ‘Xe undergoes sp³ hybridisation in 3^rd excited state.
   
3. ‘Xe’ forms 3σ-bonds and 3π-bonds with three oxygens.
4. Shape of molecule is pyramidal with bond angle 103°.
   

Question 8.
Explain the shape of XeF₄ on the basis of VSEPR theory.
Answer:
Shape of XeF₄:

1. Central atom in XeF₄ is
   
2. Xe undergoes sp³d² hybridisation in its 2^nd excited state.
3. Shape of the molecule is squãre planar with bond angle 90° and bond length 1.95A
   
4. Xe – forms four σ-bonds by the overlap of sp³d² – 2p_z(F) orbitals.

Question 9.
Which noble gas is radio active ? How is it formed?
Answer:
Radon (Rn) is radio active noble gas. Radon is obtained as decay product of ₈₆R²²⁶.
₈₆Ra²²⁶ → ₈₆Rn²²² + ₂He⁴

Question 10.
How are XeF₂, XeF₄, XeF₆ prepared? Give equation.
Answer:

Question 11.
Noble gases are inert – explain.
Answer:
Noble gases are chemically inert:

1. Noble gases have stable electronic configuration octet configuration except He.
2. Noble gases have high Ionisation energy values and have large positive values of electron gain enthalpy.

Question 12.
Write the name and formula of the first noble gas compound prepared by Bertlett.
Answer:
The first noble gas compound prepared by Bertlett is XePtF₆. Name of the compound is xenon hexa fluoro platinate.

Question 13.
Why do noble gases form compounds with fluorine and oxygen only?
Answer:
Noble gases form compounds with flourine and oxygen only.
Reason: Oxygen and Fluorine are most electronegative elements.

Short Answer Questions

Question 1.
Explain the structures of
a) XeF₂ and
b) XeF₄. (AP Mar. ‘17, IPE 16, 15, ‘14 (TS)) (TS Mar. ’14)
Answer:
Xenon forms the binary fluorides XeF₂, XeF₄, XeF₆ as follows. These are formed by direct combination of Xe and F₂.

Structure of XeF₂:

1. In XeF₂ central atom is ‘Xe’.
2. ‘Xe’ undergoes sp³d hybridisation in its 1^st excited state.
   
3. Shape of molecule is linear.
4. Xe form two σ-bonds with two fluorines.
   

b) Structure of XeF₄:

1. Central atom in XeF₄ is ‘Xe’.
2. Xe undergoes sp³d² hybridisation in it’s 2^nd excited state.
   
3. Shape of the molecule is square planar with bond angle 90° and bond length 1.95A
   
4. Xe forms four σ-bonds by the overlap of sp³d² – 2p_z (F) orbitals.

Question 2.
Explain the structures of
a) XeF₆ and
b) XeOF₄ (IPE Mar & May – 2015, 14)
Answer:
Structure òf XeF₆ is ‘Xe’.

1. Central atom in XeF₆ is ‘Xe’.
2. Xe undergoes sp³d³ hybridisation in it’s 3^rd excited state.
   
3. Shape of molecule is distorted octahedral.
   

b) Structure of XeOF₄:

1. In XeOF₄ molecule ‘Xe’ undergoes sp³d² hybridisation.
2. Shape of the molecule is square pyramid.
3. There is one Xe-O double bond containing.
   
   pπ = dπ overlapping.
   Partial hydrolysis of XeF₆ gives XeOF₄
   XeF₆ + H₂O → XeOF₄ + 2HF
   XeOF₄ is a colourless volatile liquid. It has a square pyramidal shape.

Question 3.
Explain the structure of
a) XeO₃ and
b) XeO₄ (T.S. Mar. ‘16)
Answer:
a) Structure of XeO₃:

1. Central atom is ‘Xe’
2. ‘Xe’ undergoes sp³ hybridisation in 3^rd excited state.
   
3. ‘Xe forms 3σ-bonds and 3π-bonds with three oxygens.
4. Shape of molecule is pyramidal with bond angle 103°.
   

b) Structure of XeO₄:
Xe is in sp₃ hybridisation four singma bonds and four dπ – pπ bonds. Shape of XeO₄ is tetrahedral.

Question 4.
Write the preparations of Xenon flourides.
Answer:
Xenon flourides : Xenon forms three binary fluorides, Xe F₂, XeF₄, and XeF₆ by the direct reaction of Xenon with fluorine under suitable conditions.

XeF₆ can also be prepared by the interaction of XeF₄ and O₂F₂ at 143 K.
XeF₄ + O₂F₂ → XeF₆ + O₂

Question 5.
Write the preparations of Xenon Oxides.
Answer:
Xenon Oxides: Xenon forms two oxides XeO₃ and XeO₄ with oxygen.
These oxides are formed by the hydrolysis of xenon fluorides.
6XeF₄ + 12 H₂O → 4 Xe + 2 XeO₃ + 24 HF + 3O₂
XeF₆ + 3 H₂O → XeO₃ + 6 HF

Question 6.
Give the formulae and describe the structures of a noble gas species, isostructural with
a) \(\mathrm{ICl}_4^{-}\)
b) \(\mathbf{I B r}_2^{-}\)
c) \(\mathrm{BrO}_3^{-}\)
Answer:
a) \(\mathrm{ICl}_4^{-}\) is also structural with XeF₄ and it has square planar shape.
b) \(\mathbf{I B r}_2^{-}\) is also structural with XeF₂ and it has linear shape.
c) \(\mathrm{BrO}_3^{-}\) is iso-structural with XeO₄ and it has tetrahedral šhape.

Question 7.
Write any two uses of Helium.
Answer:
Uses of Helium:

1. It is non inflammable and very light gas. Hence it is used in the balloons of Meteorological observations.
2. It is used in gas cooled nuclear reactors and used as cryogenic agent.
3. It is used as diluent for oxygen in modern diving apparatus.

Students get through AP Inter 2nd Year Chemistry Important Questions 13th Lesson Organic Compounds Containing Nitrogen which are most likely to be asked in the exam.

AP Inter 2nd Year Chemistry Important Questions 13th Lesson Organic Compounds Containing Nitrogen

Very Short Answer Questions

Question 1.
Gabriel Phthalimide synthesis exclusively forms primary amines only. Explain.
Answer:
Gabriel Phthalimide synthesis exclusively forms primary amines only.
Reason: In this reaction primary amines are formed without the traces of 2° (or) 3° amines.

Questions 2.
Write equations for carbylamine reaction of any one aliphatic amine.
Answer:
When Ethyl amine (1° – amine) reacts with chloroform in presence of alkali to form ethyl isocyanide.
CH₃ – CH₂ – NH₂ + CHCl₃ + 3KOH A CH₃ – CH₂ – NC + 3KCl + 3H₂O

Question 3.
Why aniline does not undergo Friedel — Crafts reaction?
Answer:
Aniline is a lewis base and AlCl₃ is a Lewis acid. In Friedel.Craft’s reaction both of these combined to form a complex.

Due to formation of complex the electrophilic substitution tendency decreases in aniline and it does not undergo this reaction.

Question 4.
Give structures of A, B and C in the following reactIons. [T.S. Mar. 17] [A.P. & T.S. Mar. 16]

Answer:

A – Phenyl Cyanide B – Benzoic acid C – Benzarnide

Question 5.
Why cannot aromatic primary amines be prepared by Gabriel phthalimide synthesis?
Answer:
Aromatic 1° – amines cannot be prepared by Gabriel phthalinide synthesis because aryl halides do not undergo nucleophilic substitution with an ion formed by phthalinide.

Question 6.
Accomplish the following conversions. [Mar. 14]
i) Benzolc acid to benzamide
ii) Aniline to p – bromoanlline.
Ans:
Conversion of benzoic acid to benzamide

ii) Conversion of Aniline to p – bromoanlline.

Question 7.
How are Amines prepared by Hoffmann bromamide degradation method.
Answer:
Hoffmann bromamide degradation method: In this method amides are directly converted into amines. When amides are treated with Br₅ in NaOH gives amine.

Question 8.
What is Diazotisation reaction ? Give equation. [IPE 16, 14 (T.S.)]
Answer:
Diazotisation reaction: Aromatic primary amines react with nitrous acid at low temperatures to form diazonium salts.

Question 9.
What is sulphonation ? Give equation.
Answer:
Sulphonation : Aniline reacts with cone H₂SO₄ and forms anilinium hydrogen sulphate which on heating gives P – amino benzene sulphonic acid (sulphanilic acid) which exists as Zwitter ion.

Aniline does not undergo Friedel crafts reactiondue to salt formation with AlCl₃.

Question 10.
Arrange the following bases in increasing order of their basic strength. Aniline, P – nitroaniline and P – toluidine.
Answer:
The increasing order of basic strength of given compounds is
P – nitroaniline < aniline < P – toluidine

Question 11.
How is benz ene diazonium chloride prepared? Give equation.
Answer:
Preparation: Benzene diazomum chloride is prepared by the reaction of aniline with nitrous acid at 273 – 278K. The conversion of primary aromatic amine into diazonium chloride is called Diazotisation.

Question 12.
Arrange the following bases in decreasing order of pH_b, values. C₂H₅NH₂, C₆H₅NHCH₃, (C₂H₅)₂ NH and C₆H₅NH₂.
Answer:
The decreasing order of pKb values of given amines is
C₆H₅NH₂ > C₆H₅NHCH₃ > C₆H₅NH₂ > (C₂H₅)₂ NH

Question 13.
What is a coupling reaction ? Give equation. .
Answer:
Coupling reactions : The azoproducts obtained when diazonium slats react with aromatic compounds have extended conjugated system through N = N. This reaction is called coupling reaction and the prodocuts formed are coloured.
a) Reaction with Phenol

Question 14.
How do you convert aniline to parabromo aniline. [IPE 2014]
Answer:
Aniline is first acylated to give acetaniiyde which on bromination gives parabromo derivative. This bromo derivative on hydrolysis gives parabromo aniline.

Question 15.
How is Aniline prepared. [IPE 2016 (TS)]
Answer:
Aniline is prepared by reduction of nitro benzene in acid medium.

Question 16.
Explain why ethylamine is more soluble in water where as aniline is not soluble.
Answer:
Ethyl amine is a primary amine, due to intermolecular hydrogen bonding with water molecules it is soluble in water. Though Aniline has – NH₂ group, due to hydrophobic aryl group it is not soluble in water.

Short Answer Questions

Question 1.
Explain with a suitable example how benzene sulphonylchloride can distinguish primary, secondary and tertiary amines.
Answer:
Benzene sulphonyl chloride is called Hinsberg’s reagent. This is used to distinguish the 1°, 2°, 3° – amines.

• with 1° – amine : Benzene sulphonyl chloride reacts with 1° – amine and produce N – Alkyl benzene sulphonamide which is soluble in alkali.
• with 2° – amine : Benzene sulphonyl chloride reacts with 2° – amine and produce N, N – Dialkyl benzene sulphonamide which is insoluble in alkali.
  
• with 2° – amine: Benzene suiphonyl chloride reacts with 2° – amine and produce N, N – Dialkyl benzene sulphonamide which is insoluble in alkali.
  
• with 3° – amine : Benzene sulphonyl chloride does not react with benzene sulphonyl chloride.

Question 2.
How do you prepare Ethyl cyanide and Ethyl isocyanide from a common alkylhalide ? [IPE 2014]
Answer:
Preparation of ethyl cyanide : Ethyl chloride reacts with aq. Ethanolic KCN to form Ethyl cyanide as a major product.

Preparation of Ethyl isocyanide : Ethyl chloride reacts with aq. Ethanolic AgCN to form Ethyl iso cyanide as a major product.

Question 3.
How do you distinguish cyanides and isocyanides by hydrolysis and reducation.
Answer:
i) Hydrolysis : Cyanides on hydrolysis give carboxylic acids and ammmonia where as isocynanides on hydrolysis give primary amines and formic acid:

ii) Reduction: Reducation of nitriles give primary amines where as reduction of isocyanides yield secondary amines.

Question 4.
How do you carryout the following conversions? .
i) N – Ethylamine to N, N – Diethyl propanamine
ii) Aniline to Benzene suiphonamide
Answer:
Conversion of
i) N – Ethyl amine to N, N – Diethyl propanamine : Ethyl amine reads with ethyl chloride and propyl chloride to from N, N – Di ethyl propanamine.

ii) Conversion of Aniline to Benzene sulphonamide : Aniline reacts with benzene sulphonyl chloride to form N – Phenyl benzene sulphonamide.

Question 5.
Explain the basic character of different Amines.
Answer:
Basic Character of Amines : Aniline reacts with acid and form salts.

Structure qnd Basicity : Alkyl amines are more basic than ammonia. The alkyl group pushes the electrons towards nitrogen by + I effect. Thus line pair of electrons on nitrogen are more available for sharing with the proton of acid. Hence the basic nature of alkylamines increases with increase in number of alkyl groups. Thus in gaseous phase the basicity order of amines is in the order 36 amine > 2° amine >1° amine > ammonia.

In the aqueous phase the substituted ammonium cations get stabilised by +1 effect and also by solvation with water molecules. Greater the size of the ion, lesser will be the solvation and less stabilised is the ion. The order of stability is.

Greater the stability of the ammonium cation, stronger is the basic nature of amine. The order of basicity of aliphatic amines is primary > secondary > tertiary. The – CH₃ group Creates less steric hindrance to hydrogen bortding than C₂H₅ group, thus the change of alkyl group changes the basic strength. The basic strength of methyl substituted and ethly substituted amines in aqueous soltuion is in the order.
(C₂H₅)₂ NH > (C₂H₅)₃ N > C₂H₅ – NH₂ > NH₃
(CH₃ NH)₂ > CH₃ – NH₂ > (CH₃)₃N >NH₃
Aromatic amines are less basic than ammonia. The lone pair of electrons on nitrogen is in conjugation with benzene ring.

Question 6.
Write two methods each for the preparation of alkyl cyanide and alkyl isocyanide.
Answer:
Preparation
a) From Alkyl Halides : Alkyl halides with ethanolic potassium cyanide gives cyanides where as with silver cyanide gives alkyl isocyanide.

b) From amides and aldoximes : The dehydration of amides (or) oximes with dehydrating agents like P₂O₅ (or) with benzene suiphonyl chloride yeild cyanides.

c) Isocyanides from amines: (Carbyl amine reaction)

Question 7.
Give one chemical test to distinguish between the following pairs of compounds.
i) Methylamine and dimethylamine
ii) Aniline and N.Methylanhline
iii) Ethylamine and aniline
Answer:
i) Methyl amine (1° – amine) and dimethyl amine (2° – amine) are distinguished by iso cyanide test (or) Carbylamine test. Methyl amine responds to carbylamine reaction to produce methyl isocyanide where as dimethyl amine does not respond to the iso cyanide test.

ii) Anjiine (1° – amine) and N.methyl (2° – amine) aniline are distinguished by carbylamine test (or) isocyanide test. Aniline responds to carbyl amine test to give foul smelling phenyl iso cyanide where as N – methyl aniline does not responds to carbyl amine Test.

iü) Ethyl amine (1° – aliphatic amine) and aniline (1° – aromatic amine) are distinguished by Diazotisation reaction. Aniline undergo diazotisafion reaction to form benzene diazonium salt where as ethyl amine form highly unstable alkyl diazonium salt.

Long Answer Questions

Question 1.
Explain the following name reactions: [T.S. Mar. 17] [IPE -2015, B.M.P 2016 (TS), (AP)]
i) Sandmeyer reaction
ii) Gatterman reaction
Answer:
i) Sandmeyer reaction: Formation of chiorobenzene, Bromo benzene (or) cyano benzene from benzene diazonium salts with reagents Cu₂Cl₂/HCl, Cu₂Br₂/HBr, CuCN/KCN is called sandmyeres reaction.

ii) Gatterman reaction : Formation of chioro benzene, Bromobenzene from benzene diazonium salts with reagents Cu/HCl, Cu/HBr is referred as gatterman reaction.

Question 2.
Complete the following conversions.
i) CH₃NC + HgO →
ii) ? + 2H₂O → CH₂NH₂ + HCOOH
iii) CH₃CN + C₂H₅MgBr → ?
iv) CH₃CH₂NH₂ + CHCl₃ + KOH
v)
Answer:

Question 3.
Explain why aniline in strong acidic medium gives a mixture Of Nitro anilines and what steps need to be taken to prepare selectively P – nitro aniline.
Answer:
In strong acidic medium anline undergo nitration to form mixture of nitro anilines. In strongly acidic medium aniline is protonated to form the anilinium ion which is metadirecting. So besides the ortho and para derivatives meta derivative also formed. .

By protecting – NH₂ group by acetylation reaction with acetic anhydride the nitration reaction can be controlled and the – P nitro derivative can be formed as major product.

Question 4.
Complete the following conversions : Aniline to
i) Fluorobenzene
ii) Cyanobenzene
iii) Benzene and
iv) Phenol
Answer:
i) Aniline to Fluorobenzene

iv) Aniline to phenol

Question 5.
i) Account for the stability of aromatic diazonium ions when compared to aliphatic diazonium ions.
ii) Write the equations showing the conversion of aniline diazoniumchloride to
a) chlorobenzene,
b) Iodobenzene and
c) Bromobenzene
Answer:
i) Aliphatic diazonium salts which are formed from 1° -aliphatic amines are highly unstable and liberate nitrogen gas and alcohols.

Aromatic diazonium salts formed from 1° – aromatic amines are stable for a short time in solution at low temperatures (0 – 5°C). The stability of arene diazonium ion is explained on the basis of resonance.

Question 6.
Write the steps involved in the coupling of Benzene diazonium chloride with aniline and phenol.
Answer:
Benzene diazonium chloride reacts with phenol in which the phenol molecule at its para position is coupled with the diazonium salt to form P-hydroxyazobenzene. This type of reactions is known as coupling reactions. Similarly the reaction o£ diazonium salt with aniline yields P – amino azobenzene.

Students get through AP Inter 2nd Year Chemistry Important Questions Lesson 12(b) Aldehydes, Ketones, and Carboxylic Acids which are most likely to be asked in the exam.

AP Inter 2nd Year Chemistry Important Questions Lesson 12(b) Aldehydes, Ketones, and Carboxylic Acids

Very Short Answer Questions

Question 1.
Although phenoxide ion has more resonating structures than carboxylate ion carboxylic acid is a stronger acid than phenol. Why?
Answer:

• Phenoxide ion has non-equivalent resonance structures in which the negative charge is at the less electronegative carbon atom.
• The negative charge is delocalized over two electronegative oxygen atoms in carboxylate ion whereas in phenoxide ion the negative charge is less effectively delocalized over one oxygen atom and fewer electronegative carbon atoms.
  

Question 2.
Write equations showing the conversion of
i) Acetic acid to Acetyl chloride
ii) Benzoic acid to Benzamide
Answer:
i) Acetic acid reacts with PCl₃ (or) PCl₅ (or) SOCl₂ to form acetyl chloride.

ii) Benzoic acid reacts with ammonia to form benzamide.

Question 3.
List the reagents needed to reduce carboxylic acid to alcohol.
Answer:
The reagents required to reduce carboxylic acid to alcohol are

1. LiAlH₄/Ether (or) B₂H₆
2. H₃O⁺

Question 4.
Compare the acidic strength of acetic acid, Chloroacetic acid, benzoic acid and Phenol. (IPE 2014) (Mar. ’14)
Answer:

Question 5.
Explain the position of electrophilic substitution in benzoic acid.
Answer:
Benzoic acid undergo electrophilic substitution reactions in which carboxyl group acts as a deactivating and meta directing group.

Question 6.
Write the mechanism of esterification.
Answer:
Mechanism of esterification of carboxylic acids : The esterification of carboxylic acids with alcohols is a kind of nucleophilic acyl substitution. Protonation of the carbonyl oxygen activates the carbonyl group towards nucleophilic addition of the alcohol. Proton transfer in the tetrahedral intermediate converts the hydroxyl group into – ⁺OH₂ group, which, being a better leaving group, is. eliminated as neutral water molecule. The protonated ester so formed finally loses a proton to give the ester.

Question 7.
What is Etard reaction. Give equation.
Answer:
Etard Reaction : Benzaldehyde is prepared by the oxidation of Toluene with chromyl chloride.

Question 8.
What is Gater man – Koch formylation reaction. Give equation.
Answer:
Gates man – Koch reaction:
Benzene or its derivatives treated with CO and HCl in presence of AlCl₃ gives Benzaldehyde.

Question 9.
An organic acid with molecular formula C₈H₈O₂ on decarboxylation forms Toluene. Identify the organic acid.
Answer:
The organic acid is phenyl acetic acid.

Question 10.
What is decarboxylation ? Give equation.
Answer:
Decarboxylation: Carboxylic acids lose carbon dioxide molecule to produce hydrocarbons on heating their sodium salts with soda lime (a mixutre of NaOH & CaO In ratio 3: 1).

• This reaction is called decarboxylation.
  

Short Answer Questions

Question 1.
What is Tollens reagent ? Explain its reaction with Aldehydes.
Answer:
Tollens Reagent: Freshly prepared ammonical silver nitrate solution is called Tollens reagent.

• On warming an aldehyde with Tollens reagent a bright silver mirror is produced due to formation of silver metal.
  R – CHO + 2 [Ag (NH₃)₂]⁺ + 3OH^– → RCOO^– + 2Ag + 2H₂O + 4NH₃

Question 2.
Describe the following:
i) Cross aldol condensation
ii) Decarboxylation
Answer:
i) Cross Aldol Condensation: When aldol condensation is carried out between two different aldehydes and (or) ketones, it is called cross aldol condensation.

• If both the reactants contain α-hydrogen atoms, it gives a mixture of four products.
  

Ketones can also be used as one component in the cross aldol reactions.

ii) DecarboxylationCarboxylic acids lose carbon dioxide molecule to produce hydrocarbons on heating their sodium salts with soda lime (a mixture of NaOH & CaO in ratio 3:1).

• This reaction is called decarboxylation
  

Question 3.
Explain Nucleophilic addition reaction mechanism of aldehydes and ketones.
Answer:
Nucelophilic addition reaction mechanism:

Nucleophile attack on the electrophilic carbon atom of the polar carbonyl group to form an intermediate this intermediate capture a proton to give the product. Aldehydes are more reactive towards the nucleophilic addition reaction due to steric and electronic reasons. In ketones two large substituents sterically hinder the approach of nucleophile towards carbonyl carbon. Aldehydes having only one alkyl group the attack of nucleophile is easy. Electronically two alkyl groups in ketones reduce the positive charge density on carbonyl carbon by + I effect, than aldehydes having only one alkyl group.

Question 4.
Explain the role of electron withdrawing and electron releasing groups on the acidity of carboxylic acids.
Answer:

• Electron withdrawing groups increase the acidity of carboxylic acids by stabilising the conjugate base through delocalisation of the negative charge by inductive effect.
• Electron donating groups decreases the acidity of carboxylic acids by destabilising the conjugate base.
  

Eg : Cl^– is a electron withdrawing group acidic strength order in case of chloro acetic acids CCl₃COOH > CHCl₂COOH > CH₂ClCOOH > CH₃COOH

Question 5.
Write any two methods for the preparation of Aldehydes.
Answer:
Preparation of Aldehydes:
From Hydrocarbons:
a) Hydration of alkynes in the presence of H₂SO₄ and HgSO₄ give aldehydes and ketones.

b) Reduction Acetyl Chloride (Rosen mund’s reduction)

c) From nitriles (Stephen reaction)

Nitriles are selectively reduced by di-isobutyl aluminium hydride (DIBAL – H) to imines which hydrolysis give aldehydes.

Question 6.
Write any two methods for the preparation of Ketones.
Answer:

Acyl chlorides react with dialkyl cadmium give ketones.

Question 7.
Explain the following terms. Give an example of the reaction in each ease.
i) Cyanohydrin
ii) Acetal
iii) Semicarbazone
iv) Aldol
v) Hemiacetal
vi) Oxime (IPE 2016 (TS))
Answer:
i) Cyanohyclrin
Aldehydes and ketones react with hydrogen cyanide (HCN) forms addition products called (or) known as cyanohydrins.

ii) Acetal

• In the presence of dry HCl gas, an aldehyde reacts with two equivalents of a monohydric alcohol forms gem-dialkoxy compounds are known as acetals.
• In acetal two alkoxy groups are present on the terminal C-atom.
  

iii) Semicarbazone
Aldehydes/ketones react with semicarbazide forms certain compounds called as semicarbazones.
For example:

iv) Aldol
When an aldehyde ((or) ketone) having atleast one α-hydrogen atom undergo a reaction in the presence of dilute alkali as catalyst to form aldol (or) β – hydroxy aldehydes ((or) ketals in case of ketones), the reaction is called aldol condensation.
For example:

v) Hemlacetal: In the presence of dry HCl gas an aldehyde reacts with one molecule of a monohydric alcohol forms gem-alkoxy alcohols. These are known as hemiacetals.
For example:

vi) Oxime : In weak acidic medium, an aldehyde ketone reacts with hydroxylamine forms products which are known as oxims.

Question 8.
Explain Clemenson’s reduction and Wolf Kishner reduction reactions.
Answer:
i) Clemenson’s reduction: In this reaction carbonyl group is reduced to CH₂ hence aldehydes and ketones are directly converted into alkanes. The reducing agent in this reaction is zinc amalgam and concentrated HCl.

ii) Wolf Kishner reduction : In this reaction also aldehydes and ketones are reducted to alkanes. Addition of hydrazine followed by heating in the presence of KOH in glycol gives alkanes.

Question 9.
What is haloform reaction? Give équation.
Answer:
Haloform reaction: (Oxidation of methyl ketones)
Aldehydes and ketones having at least one (CH₃CO) group react with halogens in presence of NaOH or sodium hypohalite to form haloform (CHX₃) and salt of carboxylic acids having one carbon atom less than that of carbonyl compound.

Question 10.
What is Cannizaro reaction? Give equation. (IPE – 2015 (AP), B.M.P)
Answer:
Cannizaro reaction : Aldehydes having no α – hydrogen undergo self oxidation and self reduction reaction on heating with alkali. In this reaction alcohol and salt of carboxylic acid are formed.

Question 11.
What is HVZ reaction? Give equation. (T.S. Mar.’18) (IPE 2016 (TS))
Answer:
Carboxylic acids having α-hydrogens are halogenated at the α-position on treatment with chlorine or bromine in presence of small amount of red phosphorus to give α-halo carboxylic acids.
This reaction is named as Hell-Volhard — Zelinsky (HVZ) reactions.

Question 12.
Write any three methods for the preparatión of Carboxylic acid.
Answer:
Preparation of carboxylic acids:
i) From primary alcohols : Primary alcohols on oxidation with acidified KMnO₄ (or) K₂Cr₂O₇ (or) Chromium trioxide (CrO₃) gives carboxylic acids.

ii) From Alkyl benzenes : Aromatic carboxylic acids are prepared by the oxidation of alkyl benzenes with KMnO₄ or CrO₃, any alkyl group irrespective of chain length is oxidised to -COOH.

iii) From Nitrites and Amides: Nitnies on hydrolysis in the presence of H⁺ or OH^– gives amides which on hydrolysis give acids.

Question 13.
Explain Ring substitution reactions of aromatic carboxylic acids.
Answer:
Ring Substitution : Aromatic carboxylic acids undergo electrophilic substitution at meta position. -COOH group is electron with drawing group and deactivates the ring at ortho and para position.

Question 14.
How do you prepare the following compounds from acetic acid?
i) Acetyl chloride
ii) Acetamide
iii) Acetic anhydride
iv) Ethyl alcohol
Answer:
i) Acetyl chloride: Reaction with PCl₃ (or) PCl₅ (or) SOCl₂ : Carboxylic acids form acid chlorides with PCl₃, PCl₅, SOCl₂.

ii) Acetamide formation (Reaction with ammonia) : Carboxylic acids react with Ammonia and form ammonium salt which on heating gives amides.

ii) Acetic anhydride : Carboxylic acids on heating in the presence of dehydrating agents like conc H₂SO₄, P₂O₅ give anhydride.

iv) Ethyl alcohol : Acetic acid is reduced to ethyl alcohol by LiAlH₄.

Students get through AP Inter 2nd Year Chemistry Important Questions Lesson 12(a) Alcohols, Phenols, and Ethers which are most likely to be asked in the exam.

AP Inter 2nd Year Chemistry Important Questions Lesson 12(a) Alcohols, Phenols, and Ethers

Very Short Answer Questions

Question 1.
Explain why propanol has a higher boiling point than that hydrocarbon-butane.
Answer:
Propanol has a higher boiling point (391K) than that hydrocarbon butane (309K).
Reason : In propanol strong intermolecular hydrogen bonding is present between the molecules. But in case of butane weak vander waal’s force of attractions are present.

Question 2.
Alcohols are comparatively more soluble in water than hydrocarbons of comparable molecular masses. Explain this fact.
Answer:
Alcohols are comparatively more soluble in water than hydrocarbons of comparable molecular masses.
Explanation:

• Alcohols and water are both polar solvents. Alcohol is dissolves in water, due to formation of hydrogen bonding with water molecules.
• Hydro carbons are non polar and these donot form hydrogen bonds with water molecules. So alcohols are soluble in water where as hydrocarbons are not soluble in water.

Question 3.
Name the reagents used in the following reactions.

1. Oxidation of primary alcohol to carboxylic acid
2. Oxidation of primary alcohol to aldehyde.

Answer:

1. The reagents used for the oxidation of 1° – alcohols to carboxylic acid are acidified K₂Cr₂O₇ (or) Acidic/alkaline KMnO₄ (or) Neutral KMnO₄.
2. The reagents used for the oxidation of 1°- alcohols to aldehyde are pyridine chloro chromate (PCC) in CH₂Cl₂.

Question 4.
Write any one method for the preparation of ethyl alcohol.
Answer:
From Alkenes : Alcohols can be prepared from alkenes by hydration or hydroboration oxidation.

Question 5.
What is Williamsons synthesis ? Give example. (IPE – 2016 (AP) (TS), 2015 (AP))
Answer:
Williamsons synthesis : Reaction of alkyl halide with sodium alkoxide to give ether is called Williamson’s synthesis.

Question 6.
Write the equations for the following reactions.

1. Bromination of phenol to 2, 4, 6-tribromophenol
2. Benzyl alcohol to benzoic acid.

Answer:

1. Bromination of phenol to 2, 4, 6 tribromophenol.
   
2. Benzyl alcohol to benzoic acid converted as follows.
   

Question 7.
Give the reagents used for the preparation of phenol from chlorobenzene.
Answer:
Phenol is prepared from chlorobenzene as follows. Reagents required are

1. NaOH, 623K, 300 atm,
2. HCl.

Chemical reaction:

Question 8.
what is Esterification ? Give equation.
Answer:
Esterification : Alcohols react with carboxylic acids or acid halides or acid anhydrides to form esters.

Question 9.
What is Dehydration ? Give equation.
Answer:
Dehydration : Alcohols undergo dehydration in the presence of dehydrating agents like cone H₂SO₄, (or) H₃PO₄ etc and form alkenes. The relative ease of dehydration of alcohols follows the following order. Tertiary alcohol > Secondary alcohol > primary alcohol.

Question 10.
What is Reimer Tiemann reaction ? Give equation.
Answer:
Reimer-Tiemann reaction : Phenol reacts with chloroform in presence of NaOH to form salicylaldehyde (O-Hydroxy benzaldehyde). This reaction is known as Reimer-Tiemann reaction.

Question 11.
What is Kolbe’s reaction ? Give equation.
Answer:
Kolbe’s reaction : Phenol reacts with sodium hydroxide to form sodium phenoxide. This undergoes electrophillic substitution with CO₂ to form salicylic acid.

Question 12.
Write the mechanism of the reaction of HI with methoxymethane.
Answer:
Case – I : When methoxy methane reacts with cold.dil. HI then methyl alcohol and methyl iodide are formed.
Mechanisms:

Case-II: When methoxy methane reacts with hot.conc.HI then only methyl iodide is formed.
Mechanisms:

Question 13.
Identify the reactant needed to form t-butylalcohol from acetone.
Answer:
When acetone reacts with methyl magnesium bromide followed by the hydrolysis forms t-butylalcohol.

Question 14.
Write the Oxidation reaction of phenol.
Answer:
Phenol undergo oxidation with chromicacid and forms a conjugated diketone known as benzoquinone.

Short Answer Questions

Question 1.
Give the equations for the preparation of phenol from Cumene. (TS Mar. ’17) (Mar. ’14)
Answer:
Phenol is prepared from Cumene as follows.

1. Oxidation of Cumene to Cumene hydroperoxide.
2. Cumene hydroperoxide on acidic hydrolysis to form phenol.
   

Question 2.
Explain the acidic nature of phenols and compare with that of alcohols. (AP Mar. ’17)Board Model Paper
Answer:
The reaction of phenol with sodium metal and with aq.NaOH indicates the acidic nature of phenol.
i) Phenol reacts with sodium metal to form sodium phenoxide.

ii) Phenol reacts with aq.NaOH and forms sodium phenoxide

• In phenol hydroxyl group is attached to the Sp² hydridised carbon of benzene ring which acts as electron with drawing group. The formed phenoxide ion from phenol is more stabilised due to delocalisation of negative charge.

Comparison of acidic character of Phenol and Ethanol:

• The reaction of phenol with aq. NaOH indicates that phenols are stronger acids than alcohols.
• The hydroxyl group attached to an aromatic ring is more acidic than in hydroxyl group is attached to an alkyl group.
• Phenol forms stable phenoxide ion stabilised by resonance but ethoxide ion is not.
  

Question 3.
Write the products formed by the reduction and oxidation of phenol.
Answer:
a) Reduction of phenol: Phenol undergo reduction in presence of zinc dust to form benzene.

b) Oxidation of phenol : Phenol undergo oxidation with chromic acid and forms a conjugated diketone known as benzoquinone.

Question 4.
Explain why in anisole electrophilic substitution takes place at ortho and para positions and not at meta position.
Answer:
Anisole is an aryl alkyl ether. In anisole the group -OCH₃ influences +R effect. This increases the electron density in the benzene ring and it leads to the activation of benzene ring towards electrophilic substitution reactions.

In Anisole eletron density is more at O—and P—positions but not at M—position. So O—and P-products are mainly formed during electrophillic substitution reactions.

Question 5.
Explain whý phenol with bromine water forms 2,4, 6-tribromophenol while on reaction with bromine in CS₂ at low temperatures forms para—bromophenol as the major product.
Answer:
a) Phenol undergoes Bromination in presence of CS₂ to form p—bromophenol as major product.

b) Phenol undergoes bromination in aqueous medium form 2,4,6 -tribromo phenol (white ppt).

Explanation : In bromination of phenol, the polarisation of Br₂ molecule takes place even in the absence of Lewis acid. This is due to the highly activating effect of -OH group attached to the benzene ring.

Question 6.
Explain the acidic nature of phenol.
Answer:
The reaction of phenol with sodium metal and with aq.NaOH indicates the acidic nature of phenol.
i) Phenol reacts with sodium metal to form sodium phenoxide.

ii) Phenol reacts with aq.NaOH and forms sodium phenoxide.

• In phenol hydroxyl group is attached to the Sp² hydridised carbon of benzene ring which acts as electron with drawing group. The fõrmed phenoxide ion from phenol is more stabilised due to delocalisation of negative charge.

Question 7.
Explain the electrophilic substitution reaction of Anisole.
Answer:
Electrophilic substitution in Anisole:

In all the above reactions p – isomer is the major product.

Question 8.
Write equations of the below given reactions:
i) Alkylatlon of anisole
ii) Nitration of anisole
iii) Friedel—Crafts acetylation of anisole
Answer:
i) Friedel crafts alkylation of anisole:

ii) Nitration of anisole:

iii) Friedel – Crafts acetylation of anisole

Question 9.
Illustrate hydroboration-oxidation reaction with a suitable example.
Answer:
When alkenes undergo addition reaction with diborane to form tri alkyl boranes. These followed by the oxidation by alkaline H₂O₂ to form alcohols. This reaction is called as hydroboration-oxidation reaction.

Question 10.
Write any two methods for the preparation of phenol. (IPE 2014)
Answer:
Preparation of Phenol : Phenol can be prepared from halobenzene, benzene diazonium chloride and cumene etc.
i) From halobenzene

ii) from Benzene diazonium chloride

Question 11.
Write the structures of the following compounds.
i) 2 Methyl butan -1 – o1
ii) 2, 3 – diethyl phenol
iii) 1 – ethoxy propane
iv) Cyclohexyl methanol
Answer:

Students get through AP Inter 2nd Year Chemistry Important Questions 11th Lesson Haloalkanes And Haloarenes which are most likely to be asked in the exam.

AP Inter 2nd Year Chemistry Important Questions 11th Lesson Haloalkanes And Haloarenes

Very Short Answer Questions

Question 1.
Write the structures of the following compounds. [IPE – 2015 (AP), 2016 (TS)]
i) 2-chloro-3-methylpentane,
ii) 1 -B romo4-sec-butyl-2-methylbenzene.
Answer:
i) 2-chloro-3-methyl pentane
Structure:

ii) 1-Bromo-4-sec-butyl 2-methyl benzene
Structure:

Question 2.
Which compound in each of the following pairs will react faster in S_N² reaction with -OH?
i) CH₃Br or CH₃I
ii) (CH₃)₃CCl or CH₃Cl.
Answer:
i) Among CH₃Br and CH₃I, CH₃ – I reacts faster in S_N2 reaction with OH^⊖ because bond dissociation energy of C -1 is less than the bond dissociation energy of C – Br.

ii) Among CH₃Cl and (CH₃)₃CCl, CH₃ – Cl reacts faster in S_N2 reaction with OH^⊖ because (CH₃)₃CCl has high steric hindrance than CH₃Cl.

Question 3.
Out of C₆H₅CH₂Cl and C₆H₅CHClC₆H₅, which is more easily hydrolysed aqueous KOH ?
Answer:

• Out of C₆H₅CH₂Cl and C₆H₅CHClC₆H₅ the 2nd one i.e., C₆H₅CHClC₆H₅ gets hydrolysed more easily than C₆H₅CH₂Cl.
• This can be explained by considering S_N1 reaction mechanism. In case of S_N1 reactions reactivity depends upon the stability of carbo cations.
• C₆H₅CHClC₆H₅ forms more stable carbo cation than C₆H₅CH₂Cl.
  

Question 4.
Treatment of alkyl halides with aq.KOH leads to the formation of alcohols, while in presence of alc.KOH what products are formed ?
Answer:
Treatment of alkyl halides with aq. KOH leads to the formation of alcohols. Here Nucleophillic substitution reaction takes place.
Eg. : C₂H₅Cl + aq.KOH → C₂H₅OH + KCl
Treatment of alkyl halides with alc.KOH leads to the formation of alkenes. Here elimination reaction takes place.
Eg. : C₂H₅Cl + alc. KOH → C₂H₄ + KCl + H₂O

Question 5.
What is Grignard’s reagents. How it is prepared.
Answer:
Alkyl magnesium halide is called Grignard reagent. It is prepared by the action of Mg on alkyl halide in ether solvent.
R – X + Mg → RMgX

Question 6.
What is the stereochemical result of S_N1 and S_N2 reactions? [T.S. Mar. 17 IPE 2015 (AP)]
Answer:

• The stereochemical result of S_N1 reaction is racemisation product.
• The stereochemical result of S_N2 reaction is inversion product.

Short Answer Questions

Question 1.
Define the following [A.P. Mar. 17] [IPE – 2014, 2016 (AP)]
i) Racemic mixture
ii) Retention of configuration
iii) Enantiomers.
Answer:
i) Racemic mixture: Equal portions of Enantiomers combined to form an optically inactive mixture. This mixture is called racemic mixture.

• Here rotation due to one isomer will be exactly cancelled by the rotation of due to other isomer.
• The process of conversion of enantiomer into a racemic mixture is called as racemisation.
  

ii) Retention of configuration: The preservation of integrity of the spatial arrangement of . bonds to an asymmetric centre during a chemical reaction (or) transformation is called Retention of configuration.
General Eg : Conversion of XC_abc chemical species into YC_abc.

Eg : (-) 2 – Methyl 1 – butanol conversion into (+) 1 – chloro 2. Methyl butane

Enantiomers : The stereo isomers related to each other as non-superimposable mirror images are called enantiomers. [A.P. Mar. 16]
These have identical physical properties like melting point, boiling points refractive index etc.
They differ in rotation of plane polarised light.

Question 2.
Explain the mechanism of Nucleophilic bimolecular substitution (S_N2) reaction with one example. [A.P. Mar. 18. 16] [Mar. 14]
Answer:
Nucleophilic Bimolecular substitution Reaction S_N2 :

1. The nucleophilic substitution reaction in which rate depends upon concentration of both reactants is called S_N2 reaction.
2.  It follows 2nd order kinetics. So it is called bimolecular reaction.
   Eg.: Methyl chloride reacts with hydroxide ion and forms methanol and chloride ion.
3. Here the rate of reaction depends upon the concentration of two reactants.
   
4. In the above mechanism the configuration of carbon atom under attack inverts in much the same way as an umbrella is turned inside out when caught in a strong wind. This process is called inversion of configuration.
5. In transition state the carbon atom is simultaneously bonded to the incoming nucleophile and out going group. It is very unstable.
6. The order of reactivity for SN2 reactions follows : 1°-alkyl halides > 2°-alkyl halides > 3°-alkyl halides.

Question 3.
Explain why allylic and benzylic halides are more reactive towards S_N1 substitution while 1-halo and 2-halobutanes preferentially undergoes S_N2 substitution.
Answer:

1. Allylic and benzylic halides show high reactivity towards the S_N1 reaction.
   Reason : The carbocation thus formed gets stabilised through resonance phenomenon as shown below.
   
2. 1-halo and 2-halo butanes preferentially undergoes S_N2 substitute.
   Reason : S_N2 reactions involve transition state formation. Higher the steric hindrance lesser the stability of transition state. The given 1 -halo and 2-halo butanes have less steric hindrance. So these are preferentially undergo S_N2 reaction.

Question 4.
Write the preparations of Alkyl halides.
Answer:

Preparation ofAlkyl Halides :
i) From Alcohols : Alkyl halides are prepared by the action of HX, PX₃, PX₃, PX₅, X₂ & red phosphurs or SOCl on alcohols.

Question 5.
Explain SN¹ and SN² reactions. [T.S. Mar. 18] [IPE – 2016, 2015, 2014 (TS)]
Answer:
i) SN¹: Substitution nucleophilic unimolecular reaction: In this reaction the first step is the formation of stable carbonium ion. This step is slow and is the rate determining step. The alkyl halides which form stable carbonium ion follow SN¹ reaction.

The order of reactivity of alkyl halides towards SN¹ reaction.
Tertiary halide > Secondary halide > Primary halide > CH₃ – X.
Benzyl halide and allyl halides are primary halides but participate in SN¹ mechanism due to the formation of stable benzyl and allyl carbonium ions (Benzyl and allyl carbonium ions are stabilised due to resonance).

ii) SN²: Substitution nucleophilic bimolecular reaction: In this reaction the rate of reaction depends on the concentration of alkyl halide and also on the concentration of nucleophile hence it is a bimolecular reaction.

The order of reactivity of alkyl halides towards SN2 reaction.
CH₃ – X > Primary halide> Secondary halide > Tertiary halide
For a given alkyl group, the reaction of the alkyl halide, R – X follows the same order in both the mechanisms R – I > R – Br> R – Cl > R – F

Question 6.
What is Wurtz reaction ? Give equation.
Answer:
Wurtz Reaction : Alkyl halides react with sodium in dry ether solvent give alkanes.

Question 7.
Explain different chemical properties of Alkyl halide. [IPE 2016 (TS)]
Answer:

Question 8.
Explain Wurtz – Fittig and Fittig reactions. [A.P. Mar. 17]
Answer:
i) Wurtz – Fittig reaction : The reaction of aryl halide with alkyl halide in the presence of sodium in ether to give alkyl benzene is called Wurtz Fittig reaction.

ii) Fittig reaction : Aryl halides react vith sodium in dry ether solvent to give diphenyl is called fitting reaction.

Question 9.
Write any one method for the preparation of chloro benzene.
Answer:
Chlorination of benzene in the pressence of Lewis acid like AlCl₃, FeCl₃ gives chioro benzene.

Question 10.
Explain electrophilic substitution reactions of chioro benzene.
Answer:
Electrophilic Substitution Reaction : Halogen atom is electron releasing group. it activates the benzene ring hence electrophilic substitution takes place at ortho and para positions.

Question 11.
Write the structures of the following organic halides. [IPE 2016 (T.S)]
i) 1 -Bromo-4-sec-butyl-2-methylbenzene,
ii) 2-Chioro- 1 -phenylbutane
iii) p-bromochlorobenzene,
iv) 4-t-butyl-3-iodoheptane.
Answer:
i) 1 -Bromo-4-sec-butyl-2-methylbenzene,
Structure :

ii) 2-Chioro- 1 -phenylbutane
Structure :

iii) p-bromochlorobenzene,
Structure :

iv) 4-t-butyl-3-iodoheptane.
Structure :

Students get through AP Inter 2nd Year Chemistry Important Questions 10th Lesson Chemistry In Everyday Life which are most likely to be asked in the exam.

AP Inter 2nd Year Chemistry Important Questions 10th Lesson Chemistry In Everyday Life

Very Short Answer Questions

Question 1.
What are drugs?
Answer:
Drug: The chemicals of low molecular masses ranging from 100 to 500 U that react with macromolecular targets to produce biological responses are called drugs.
E.g. : Morphine, Codeine, Heroin etc.,

Question 2.
When are the drugs called medicines?
Answer:
When the biological response of a drug is therapeutic and useful then the chemical substances (drugs) are called medicines.

Question 3.
Define the term chemotherapy.
Answer:
Chemotherapy: The use of medicines (chemical substances) in the treatment of diseases is called chemotherapy.
In chemotherapy diagnosis, prevention and treatment of diseases are involved.

Question 4.
What are antagonists and agonists ?
Answer:

1. Antagonists : The drugs that bind to the receptor site and inhibit its natural function are called antagonists. ’
   • These are useful when blocking of message is required.
2. Agonists : The drugs that mimic the natural messenger by switching on receptors are called agonists.
   • These are useful when there is lack of natural chemical messenger.

Question 5.
What are antacids ? Give example. [IPE – 2014, 2016 (TS)] [Mar. 14]
Answer:
Antacids : Chemicals that remove the excess of acid in the stomach and maintain the pH to normal level are antacids.
E.g. : Omeprozole, Lansoprozole etc.

Question 6.
What are antihistamines ? Give example. [IPE 2014]
Answer:
Antihistamines : Chemicals that prevent the interaction of histamines with receptors of the stomach wall thus producing less amount of acid are antihistamines.
E.g. : Dimetapp, Terfenadine (Seldane).

Question 7.
What are tranquilizers ? Give example. [IPE 2015 (TS)]
Answer:
Tranquilizers : The drugs which are used in the management (or) treatment of psychoes and neuroses are called tranquilizers. ‘
E.g.: Luminal, Seconal, Barbituric acid etc.

Question 8.
What are analgesics ? How are they classified ?
Answer:
Analgesics : These are to reduce or totally abolish pain without causing impairment of consciousness, mental confusion, incoordination, paralysis, disturbances of nervous system etc.
Analgesics are classified as

1. Narcotic analgesics : These are most potent and clinically useful agents causing depression of central nervous system and at the same time act as strong analgesics. E.g. : Morphine, Codeine etc.
2. Non-narcotic analgesics : These drugs are analgesics but they have no addictive
   properties. Their analgesic use is limited to mild aches and pains. .
   E.g.: Aspirin, Ibuprofen etc.

Question 9.
What are antimicrobials ?
Answer:
Antimicrobials : The chemical substances which destroy (or) prevent the development (or) inhibit the pathogenic action of microbes such as bacteria, fungi, virus are called antimicrobials.
E.g.: Lysozyme, Lactic acid etc.

Question 10.
What are antibiotics ? Give example. [A.P. Mar. 16]
Answer:
Antibiotics: The chemical substances produced by micro organisms and inhibit the growth or destroy microorganisms are called antibiotics.
(Or)
The substance produced totally or partly by chemical synthesis which in low concentration inhibits the growth (or) destroy microorganism by intervening in their metabolic process are called antibiotics.
E.g.: Penicillin, Chloramphenicol etc.

Question 11.
What are antiseptics ? Give example. [A.P. Mar. 15]
Answer:
Antiseptics : The chemical compounds that kill (or) prevent the growth of micro organism are called antiseptics.
Antiseptics are the chemical substances applied on the living tissues such as wounds, cuts, ulcers and diseased skin surfaces.
E.g.: Dettol, Bithional etc.

Question 12.
What are disinfectants ? Give example. [A.P. Mar. 17]
Answer:
Disinfectants : The chemical compounds used for killing (or) preventing the growth of microorganism are called disinfectants.
i) These are applied to inanimate objects like floors, drainage systems etc.
E.g.:

1. 4% aqueous solution of formaldehyde called formalin is a disinfectant
2. 0.3 ppm chlorine aqueous solution is disinfectant.
3. SO₂ in very low concentration is disinfectant.

Question 13.
What is the difference between antiseptics and disinfectants ?
Answer:
Antiseptics are the chemical substances applied on the living tissues such as wounds, cuts, ulcers and diseased skin surfaces.
Disinfectants are applied to inanimate objects such as floors, drainage system, instruments etc.

Question 14.
What are antifertility drugs ? Give example.
Answer:
Antifertility drugs: These are birth control pills and contain a mixture of synthetic estrogen and progesterone derivatives.
E.g. : Norethindrone, Ethynylestradiol (novestrol)

Question 15.
What are artificial sweetening agents ? Give example. [IPE – 2016 (A.P.), (T.S.)]
Answer:
The chemical substances which are used instead of sucrose (or) sugar are called artificial sweetening agents.
E.g. : Aspartame, Alitame, saccharin.
These decrease the calorific intake and at the same time several times sweeter than sucrose.

Question 16.
Why is the use of aspartame limited to cold foods and drinks ?
Answer:
Aspartame is unstable at cooking temperature so it’s use is limited to cold foods and soft drinks.

Question 17.
What problem does arise in using alitame as artificial sweetener ?
Answer:
While using alitame as artificial sweetener, the control of sweetness of food is difficult. Alitame is a high potency sweetner.

Question 18.
Why do soaps not work in hard water ?
Answer:
In hard water Ca, Mg-dissolved salts are present. Ca⁺², Mg⁺² ions form insoluble Ca, Mg, soaps respectively when sodium (or) potassium soaps are dissolved in hard water.

1. These insoluble soaps separate as scum in water and are useless as cleansing agent. ’ These are problematic to good washing because the ppt adheres into the fibres of cloth
   as gummy mass.
2. Hair washed with hard water looks dull.
3. Dye does not absorb evenly on cloth washed with soap using hard water due to this gummy mass.

Question 19.
What are synthetic detergents ?
Answer:
The cleansing agents which are having all the properties of soaps but donot contain any soap are called synthetic detergents.
Synthetic detergents can be used both in soft and hard water as they give foam even in hard water.
E.g.: Sodium dodecyl benzene sulphonate.

Question 20.
What is the difference between a soap and a synthetic detergent ?
Answer:

1. Generally soaps are sodium or potassium salts of long chain fattyacids.
2. Synthetic detergents are cleansing agents having all the properties of soaps and donot cpntain any soap.
3. Soaps donot work in hard water but synthetic detergents can be used both in soft and hard water as they give foam even in hard water. Some of the detergents give foam even in ice cold water.

Question 21.
What are food preservatives ? Give example. [A.P. Mar. 17 – IPE 2016 (T.S)]
Answer:
The chemical substances which prevent the spoilage of food due to microbial growth are called food preservatives.
E.g.: Sodium benzoate, Salt of sorbic acid etc.

Question 22.
How are synthetic detergents better than soaps ?
Answer:
Soaps donot work in hard water but synthetic detergents can be used both in soft and hard water as they give foam even in hard water. Some of the detergents give foam even in ice cold water.

Question 23.
Name a substance which can be used as an antiseptic as well as disinfectant.
Answer:
Phenol is used as antiseptic as well as disinfectant.

1. 0.2% phenol is antiseptic
2. 1% phenol is disinfectant.

Question 24.
Why chemicals are added to food ?
Answer:
Chemicals are added to food for i) preservation ii) enhancing their appeal iii) adding nutritive value in them.

Question 25.
Name different categories of food additives.
Answer:
The following are the categories of food additives.

1. Food colours
2. Flavours and sweetners
3. Fat Emulsifiers and stabilising agents
4. Anti oxidants
5. Flour improvers – antistaling agents and bleaches
6. Preservatives
7. Nutritional supplements such as minerals, vitamins and amino acids.

Question 26.
Why do we require artificial sweetening agents ?
Answer:

1. Artificial sweetening agents are very useful to diabetic persons.
2. These decrease the calorific intake and at the same time several times sweeter than sucrose.
3. These are harmless.

Question 27.
Name the sweetening agent used in the preparation of sweets for a diabetic patient.
Answer:
The sweetening agent used in the preparation of sweets for a diabetic patient is saccharin (or) sucralose. It is stable at cooking temperature.

Question 28.
Name two most familiar antioxidants used as food additives.
Answer:
The most familiar antioxidants are butylated hydroxy toluene (BHT) and butylated hydroxy anisole (BHA).

Question 29.
What is saponification ?
Answer:
The process of formation of soaps containing sodium salts by heating esters of fatty acid with aq. NaOH solution is called saponification.

Question 30.
What are the main constituents of dettol ?
Answer:
Dettol (antiseptic) is a mixture of chloroxylenol and terpineol.

Question 31.
What is tincture of iodine ? What is its use ?
Answer:
Tincture of iodine (antiseptic) is a mixture of 2 – 3% Iodine solution in alcohol-water.

Question 32.
What are enzymes and receptors ?
Answer:
Enzymes : The proteins which perform the role of biological catalysts in the body are called enzymes.
Receptors : The proteins which are crucial to communication system in the body are called receptors.

Question 33.
Which forces are involved in holding the drug to the active site of enzymes ?
Answer:
The forces involved in holding the drugs to the active site of enzymes are ionic bonds, vander waal’s forces, hydrogen bonds, dipole-dipole interactions etc.

Question 34.
What are enzyme inhibitors ?
Answer:
The drugs which inhibits the catalytic activity of enzymes and can block the binding site of the enzyme and prevent the binding of substrate are called enzyme inhibitors.

Question 35.
While antacids and antiallergic drugs interfere with the function of histamines why do not these interfere with the function of each other ?
Answer:
Antacids and antiallergic drugs donot interfere with the function of each other because they work on different receptors in the body.

Question 36.
What are antipyretics ? Give example.
Answer:
The medicines which reduce body temperature during fever are called antipyretics.
E.g.: Paracetamol

Short Answer Questions

Question 1.
What are analgesics ? How are they classified ? Give examples.
Answer:
Analgesics : These are to reduce or totally abolish pain without causing impairment of consciousness, mental confusion, incoordination, paralysis, disturbances of nervous system etc. Analgesics are classified as

1. Narcotic analgesics : These are most potent and clinically useful agents causing depression of central nervous system and at the same time act as strong analgesics.
   E.g. : Morphine, Codeine etc.
2. Non-narcotic analgesics : These drugs are analgesics but they have no addictive properties. Their analgesic use is limited to mild aches and pains.
   E.g. : Aspirin, Ibuprofen etc.

Question 2.
What are different types of microbial drugs ? Give one example for each.
Answer:
Antimicrobials : The chemical substances which destroy or prevent the development (or) inhibit the pathogenic action of microbes such as bacteria, fungi, virus are called antimicrobials.
E.g.: Lysozyme, Lactic acid etc.,
Different types of antimicrobial drugs are antibiotics, antiseptics, disinfectants.

1. Antibiotics : The chemical substances produced by micro organisms and inhibit the growth or destroy microorganisms are called antibiotics.
   (Or)
   The substance produced totally or partly by chemical synthesis in low concentration inhibits the growth (or) destroy microorganism by intervening in their metabolic process are called antibiotics.
2. Antiseptics: The chemical compounds that kill (or) prevent the growth of micro organism are called antiseptics.
   Antiseptics are the chemical substances applied on the living tissues such as wounds, cuts, ulcers and diseased skin surfaces.
3. Disinfectants : The chemical compounds used for killing (or) preventing the growth of microorganism are called disinfectants.
   These are applied to inanimate objects like floors, drainage systems etc.
   E.g. :
   • 4% aqueous solution of formaldehyde called formalin is a disinfectant
   • 0.3 ppm chlorine aqueous solution is disinfectant.
   • SO₂ in very low concentration is disinfectant.

Question 3.
Write notes on antiseptics and disinfectants. [T.S. Mar. 17]
Answer:
Antiseptics : The chemical compounds that kill (or) prevent the growth of micro organism are called antiseptics.
Antiseptics are the chemical substances applied on the living tissues such as wounds, cuts, ulcers and diseased skin surfaces.
E.g.: Dettol, Bithional etc.
Phenol is used as antiseptic as well as disinfectant. 0.2% phenol is antiseptic.
Dettol (antiseptic) is a mixture of chloroxylenol and terpineol.
Tincture of iodine (antiseptic) is a mixture of 2 – 3% Iodine solution in alcohol-water.

Disinfectants : The chemical compounds used for killing (or) preventing the growth of microorganism are called disinfectants.
These are applied to inanimate objects like floors, drainage systems etc.
E.g.:

1. 4% aqueous solution of formaldehyde called formalin is a disinfectant.
2. 0.3 ppm chlorine aqueous solution is disinfectant.
3. SO₂ in very low concentration is disinfectant.

Phenol is used as antiseptic as well as disinfectant. 1% phenol is disinfectant.

Question 4.
How do antiseptics differ from disinfectants ? Does the same substance be used as both ? Give one example for each.
Answer:
Antiseptics are the chemical substances applied on the living tissues such as wounds, cuts, ulcers and diseased skin surfaces.
Disinfectants are applied to inanimate objects such as floors, drainage system, instruments etc.
Phenol is used as antiseptic as well as disinfectant.
i) 0.2% phenol is antiseptic.
ii) 1% phenol is disinfectant.

1. Examples of Antiseptics :
   • Dettol (antiseptic) is a mixture of chloroxylenol and terpineol.
   • Tincture of iodine (antiseptic) is a mixture of 2.3% Iodine solution in alcohol-water.
2.  Examples of disinfectants :
   • 4% aqueous solution of formaldehyde called formalin is a disinfectant.
   • 0.3 ppm chlorine aqueous solution is disinfectant.
   • SO₂ in very low concentration is disinfectant.

Question 5.
Explain the following terms with suitable examples.
i) Cationic detergents
ii) Anionic detergents
iii) Non-ionic detergents
Answer:
Synthetic detergents are classified into three types.
i) Cationic detergents : These are synthetic detergents.
a) Cationic detergents are quarternary ammonium salts of amines with acetates, chlorides (or) bromides as anions.

b) Cationic part possess a long hydrocarbon chain and a positive charge on nitrogen atom. Hence these are called cationic detergents.
E.g.: Cetyl trimethyl ammonium bromide
It is used in hair conditioners.

ii) Anionic Detergents : These are synthetic detergents.
a) Anionic detergents are sodium salts of sulphonated long chain alcohols (or) hydrocarbons.
b) Anionic detergents are formed by the treatment of long chain alcohols with cone. H₂SO₄ followed by the neutralisation with alkali.
E.g.: Sodium lauryl sulphate.

These are used for house hold work and in tooth pastes.

iii) Non-ionic detergents : These are synthetic detergents.
a) Non-ionic detergents donot contain any ion in their constitution..
b) The detergent formed by the reaction of stearic acid with poly ethylene glycol is an example of non ionic detergent.

Non-ionic detergents are used in liquid dish washing purpose.

Question 6.
What are biodegradable and non-bio degradable detergents ? Give one example for each.
Answer:
i) Biodegradable detergents :

• The detergents which are degraded (or) decomposed by micro organisms are called biodegradable detergents. Biodegradable detergents have less branching.
• These do not cause water pollution.
  E.g. : n-dodecyle benzene sulphonate, soap (non synthetic)

ii) Non Biodegradable detergents :

• The detergents which are not decomposed (Or) degraded by microbes (or) micro organisms are called non-biodegradable detergents. These have more branching.
• These cause water pollution.
  E.g.: ABS detergent.

Question 7.
What are broad spectrum and narrow spectrum antibiotics ? Give one example for each.
Answer:
The range of bacteria (or) other micro organisms that are effected by a certain antibiotic is expressed as its spectrum of action.
Broad spectrum antibiotics : Antibiotics which kill (or) inhibit a wide range of gram¬positive and gram-negative bacteria are called broad spectrum antibiotics.

Narrow spectrum antibiotics: Antibiotics which are effective mainly against gram-positive (or) gram-negative bacteria are called narrow spectrum antibiotics.
E.g.: Penicillin – G is a narrow spectrum antibiotic.

Limited spectrum antibiotics : Antibiotics which are effective mainly against a single organism (or) disease are called as limited spectrum antibiotics.

Question 8.
Name different types of soaps.
Answer:
The following are the different types of soaps.

1. Toilet soaps
2. Soaps that float in water
3. Medicated soaps
4. Shaving soaps
5. Laundry soaps
6. Soap powders and scouring soaps etc.

Question 9.
Write notes on antioxidants in food.
Answer:
Antioxidants :

• Antioxidants are important and necessary food additives.
• Antioxidants help in food preservation by retarding the action of oxygen on food.
• Antioxidants are more reactive towards oxygen than the food material which they protect.
• The most familiar antioxidants are Butylated hydroxy toluene (BHT) and Butylated hydroxy anisole (BHA).
• The addition of BHA to butter increases its shelf life from months to years.
• BHT and BHA along with citric acid are added to produce more antioxidant effect.
• SO₂ and sulphites are useful anti oxidants for wine and beer, sugar syrups and cut, peeled (or) dried fruits and vegetables.