AP State Syllabus AP Board 6th Class Maths Solutions Chapter 10 Practical Geometry InText Questions and Answers.
AP State Syllabus 6th Class Maths Solutions 10th Lesson Practical Geometry InText Questions
![]()
Check Your Progress (Page No. 139)
Question 1.
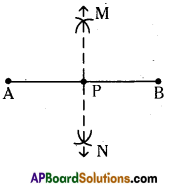
Measure the lengths of [latex]\overline{\mathrm{AP}}[/latex] and [latex]\overline{\mathrm{PB}}[/latex] in both the constructions. What do you observe?
Solution:
In the construction we observe that [latex]\overline{\mathrm{AP}}=\overline{\mathrm{PB}}[/latex]
That is P can divide AB into two equal parts.
Let’s Think (Page No. 140)
Question 1.
In the construction of perpendicular bisector in step 2, what would happen if we take the length of radius to be smaller than half the length of [latex]\overline{\mathrm{AB}}[/latex] ?
Solution:
If we take the length of radius to be smaller than half the length of [latex]\overline{\mathrm{AB}}[/latex]
Arcs cannot intersect each other. So, we can’t construct the perpendicular bisector to the given line [latex]\overline{\mathrm{AB}}[/latex]
![]()
(Page No. 144)
Question 1.
Construct angles of 180°, 240°, 300°.
Solution:
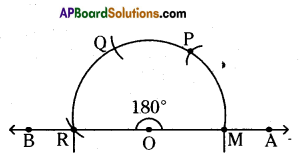
i) ∠AOB = 180°
Steps of construction:
- Draw any ray [latex]\overline{\mathrm{OA}}[/latex] of any length.
- Place the pointer of the compasses at ‘O’ with ‘O’ as centre any convinient radius draw an arc cutting OA at M.
- With M as centre and without altering radius draw an arc which cuts the previous arc at P.
- Draw an arc with the same radius from P which cuts the previous arc at Q and from Q draw another arc which meets at R.
- Join OR. ( [latex]\overline{\mathrm{OB}}[/latex] ). Then ∠AOB is the required angle.
Hence the required angle ∠AOB = 180° is constructed.
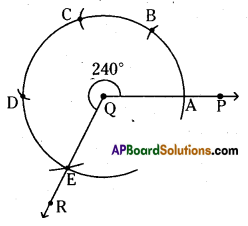
ii) ∠PQR = 240°
Steps of construction:
- Draw any ray [latex]\overline{\mathrm{QP}}[/latex] of any length.
- Place the pointer of the compasses at O with ‘O’ as centre any convinient radius draw an arc cutting QP at A.
- With A as centre and without altering radius draw an arc which cuts the previous arc at B.
- Draw an arc with the same radius from B which cuts the previous arc at C and from C draw another arc which meets at D.
- Draw an arc with the same radius from D draw an arc which cuts the previous arc at E.
- Join [latex]\overrightarrow{\mathrm{QE}}(\overrightarrow{\mathrm{QR}})[/latex]. Then ∠PQR is the required angle.
Hence the required angle ∠PQR = 240° is constructed.
![]()
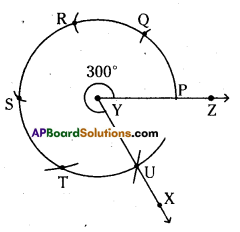
iii) ∠XYZ – 300°
Steps of construction :
- Draw any ray [latex]\overline{\mathrm{YZ}}[/latex] of any length.
- Place the pointer of the compasses at Y with Y as centre any convinient radius draw an arc cutting YZ at P.
- With P as centre and without altering radius draw arc which quts the previous arc at Q and from Q draw another arc which cuts the previous arc at R.
- Draw an arc with the same radius from R which cuts the previous arc at S and from S draw another arc which meets at T.
- Draw an arc with the same radius from T which cuts the previous arc at U.
- Join [latex]\overrightarrow{\mathrm{YU}}(\overrightarrow{\mathrm{YX}})[/latex]. Then ∠XYZ is required angle.
Hence the required angle ∠XYZ = 300° is constructed.
(Page No. 145)
Question 1.
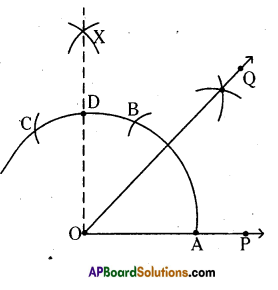
Construct an angle of 45° by using compasses.
Solution:
45°
Steps of construction :
i) Draw any ray [latex]\overline{\mathrm{OP}}[/latex] of any length.
ii) Draw arcs with the same radius from A to B and from B to C which cuts the previous arc at B and C respectively.
iii) Draw arcs from B and from C with same radius which can intersect at X.
iv) Join [latex]\overrightarrow{\mathrm{OX}}(\overrightarrow{\mathrm{OD}})[/latex] i.e., ∠POD = 90°.
v) Draw the bisector to ZPOD which is [latex]\overrightarrow{\mathrm{OQ}}[/latex]
vi) Now, ∠POQ = ∠QOD = [latex]\frac{\angle \mathrm{POD}}{2}=\frac{90}{2}[/latex] = 45°
∴ ∠POQ = 45° (Q.E.D)

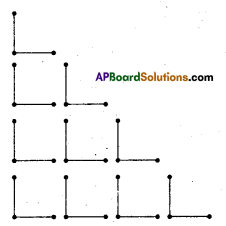
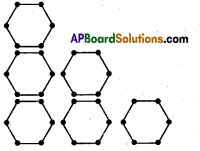
 Continue the same shape for 2 times, 3 times and 4 times. Frame the rule for repeating the pattern.
Continue the same shape for 2 times, 3 times and 4 times. Frame the rule for repeating the pattern.