AP Board 9th Class Maths Solutions Chapter 15 గణితములో నిరూపణలు InText Questions

AP SCERT 9th Class Maths Textbook Solutions Chapter 15 గణితములో నిరూపణలు InText Questions and Answers.

AP State Syllabus 9th Class Maths Solutions 15th Lesson గణితములో నిరూపణలు InText Questions

ఇవి చేయండి.

1. ఏవైనా 5 వాక్యములు రాసి అవి సత్యమో/అసత్యమో నిర్ణయించి, కారణాలు తెల్పంది. (పేజీ నెం. 311)
సాధన.
(i) 9 ప్రధాన సంఖ్య – అసత్యము
ఇది ఒక ప్రవచనము ఎందుకనగా దీని సత్య విలువను మనము చెప్పగలము. ఇది అసత్యము. ‘9’ కి (1 మరియు 9) కాక ఇంకనూ కొన్ని కారణాంకాలు గలవు.
(ii) x విలువ 5 కన్నా తక్కువ – సత్యమో లేక అసత్యమో చెప్పలేము.
ఇది ప్రవచనము కాదు ఎందుకనగా ఇది సత్యమో లేక అసత్యమో చెప్పలేము. కావున ఇది ఒక వాక్యము మాత్రమే.
(iii) 3 + 5 = 8 – సత్యము
పై వాక్యము సత్యము కావున ఇది ఒక ప్రవచనము.
(iv) రెండు బేసి సంఖ్యల మొత్తము సరిసంఖ్య – సత్యము. పై వాక్యము సత్యమని సరి చూచుటకు 3 + 5 = 8 లేక, 5 + 7 = 12 వంటి విలువలను తీసుకుంటారు. కావున ఈ వాక్యము ఒక ప్రవచనము.
(v) \(\frac {x}{2}\) + 3 = 9 – ఇది సత్యమో లేక అసత్యమో చెప్పలేము.
పై వాక్యము ప్రవచనము కాదు. ఎందుకనగా x విలువ లేకుండా సత్య విలువను నిర్ధారించలేము.

ప్రయత్నించండి

1. 1. 3 ఒక ప్రధాన సంఖ్య
2. రెందు బేసి సంఖ్యల లబ్ధము ఒక సరిసంఖ్య.
3. x ఏదైనా ఒక వాస్తవ సంఖ్య అయితే 4x + x = 5x
4. భూమికి కల ఒకే ఒక ఉపగ్రహము చంద్రుడు.
5. రాము ఒక మంచి డ్రైవరు.
6. “లీలావతి” అను గ్రంథమును భాస్కరుడు రచించెను.
7. అన్ని సరి సంఖ్యలు సంయుక్త సంఖ్యలు.
8. రాంబస్ ఒక చతురస్రము.
9. x > 7.
10. 4 మరియు 5 పరస్పర ప్రధాన సంఖ్యలు.
11. సిల్వర్ ఫిష్ అను చేప సిల్వర్ తో చేయబడింది.
12. భూమిని పరిపాలించుటకు మనుష్యులు కలరు.
13. x ఏదైనా ఒక వాస్తవ సంఖ్య అయిన 2x > x.
14. క్యూబా రాజధాని హవానా.
పై వాక్యములలో ప్రత్యుదాహరణల ద్వారా, అసత్యమని నిర్ణయించగల ప్రవచనములు ఏవి ? (పేజీ నెం. 312)
సాధన.
ప్రవచనాలు – 2, 7, 8, 13 లను ఒక ప్రత్యుదాహరణ ద్వారా నిర్ణయించవచ్చును.
2. రెండు బేసి పూర్ణ సంఖ్యల లబ్దము సరిసంఖ్య.
ప్రత్యుదాహరణ : 3 మరియు 5 లు చేసి పూర్ణ సంఖ్యలు. కావున వాటి లబ్ధము 3 × 5 = 15 సరిసంఖ్య కాదు.
7. అన్ని సరిసంఖ్యలు సంయుక్త సంఖ్యలు.
ప్రత్యుదాహరణ : ‘2’ సరి ప్రధాన సంఖ్య.
8. ఒక రాంబస్, చతురస్రము.

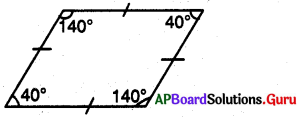
ప్రత్యుదాహరణ : 40°, 140°, 40°, 140°లు కావున ఇది ఒక రాంబస్.
13. 2x > x, x ఏదేని సంఖ్య అయిన
ప్రత్యుదాహరణ : x = – 3 అయిన 2x = 2 (-3) = – 6
ఇక్కడ – 6 < – 3 అగును.

2. పైథాగరస్ యొక్క ప్రజాదరణ దృష్యా వారి అనుయూయుదొకడు లంబకోణ త్రిభుజ భుజాల మధ్య మరొక సంబంధం కలదని భావించాడు. (పేజీ నెం. 319)

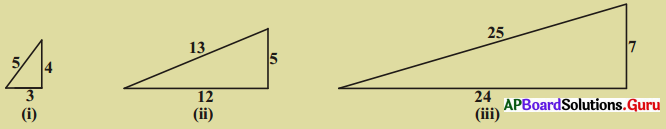
సాధన.
ఈ భావన పై త్రిభుజాలకు సత్యము.
(i) 3² = 5 + 4
9 = 5 + 4
(ii) 5² = 25 = 12 + 13
25 = 12 + 13
(iii) 7² = 49 = 24 + 25
49 = 24 + 25
కాని ఈ నియమం చిన్న సంఖ్య భుజంకు వర్తించదు.
ఉదా :

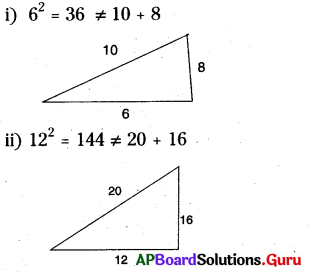
సిద్ధాంతములు :

1. త్రిభుజములోని మూడు కోణముల మొత్తం 180°. (పేజీ నెం. 318)

2. రెండు బేసి సంఖ్యల లబ్ధం, బేసిసంఖ్య. (పేజీ నెం. 318)

3. రెండు వరుస సరి సహజ సంఖ్యల లబ్ధం, 4 చే భాగింపబడుతుంది. (పేజీ నెం. 318)

4. ఒక త్రిభుజములోని మూడు అంతర కోణముల మొత్తం 180°. (పేజీ నెం. 324)
సాధన.
నిరూపణ : ABC ఒక త్రిభుజము.
\(\angle \mathrm{ABC}+\angle \mathrm{BCA}+\angle \mathrm{CAB}\) = 180° అని నిరూపించవలెను

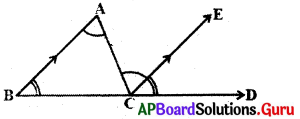
BA కు సమాంతరంగా C నుండి CE అను రేఖను గీయుము.
BC ను D వరకు పొడిగించండి.
CE | | BA మరియు AC ఒక తిర్యగ్రేఖ.
కావున \(\angle \mathrm{CAB}=\angle \mathrm{ACE}\) (ఏకాంతర కోణాలు) ……………….(1)
అదే విధంగా \(\angle \mathrm{ABC}=\angle \mathrm{DCE}\) (సదృశ కోణాలు) ………….. (2)

నీవు ఈ సిద్ధాంతము 4వ అధ్యాయములో నేర్చుకొన్నదే. మనము సిద్ధాంతాల నిరూపణకు తరచుగా వాటి పటాలను గీయుట చాలా ముఖ్యము. అయినప్పటికి నిరూపణ అనునది తార్కికంగా ఉండవలెను. సామాన్యంగా ఆ రెండు రేఖలు లంబంగా ఖండించుకొనునట్లు కన్పించుచున్నది కావున ఆ రెండు కోణాల కొలతలు 90° అంటాం. ఇలాంటి తర్కములో మోసపోవచ్చు. కాబట్టి తగు జాగ్రత్త అవసరము.

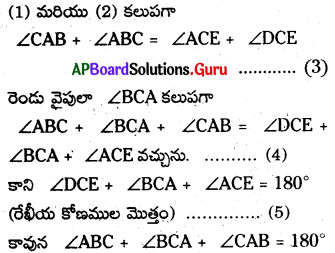
పై నిరూపణలోని ప్రతి వివరణ వెనుక కల కారణాలు పరిశీలిద్దాము.
సోపానము 1: పై సిద్ధాంతం త్రిభుజ ధర్మాలపై ఆధారపడి ఉన్నది. కావున త్రిభుజం ABCతో ప్రారంభిద్దాం.

సోపానము 2 : సిద్ధాంతంలో BA కు సమాంతరంగా CE గీసి, BCను D వరకు పొడిగించితిమి. నిరూపణకు ఇది చాలా ముఖ్యమైన సోపానము.

సోపానము 3 : మనకు తెలిసిన పూర్వ సిద్ధాంతాల ఆధారంగా ఏకాంతర కోణాలు సదృశకోణాల ధర్మాల ఆధారంగా \(\angle \mathrm{CAB}=\angle \mathrm{ACE}\) మరియు \(\angle \mathrm{ABC}=\angle \mathrm{DCE}\) అని చెప్పగలము.

సోపానము 4 : “ఒక సమీకరణమునకు రెండువైపులా సమాన అంశములు కలిపిన ఆ సమీకరణములో మార్పు ఉండదు” అను యూక్లిడ్ సామాన్య భావన ఆధారంగా \(\angle \mathrm{ABC}+\angle \mathrm{BCA}+\angle \mathrm{CAB}=\angle \mathrm{DCE}+\angle \mathrm{BCA}+\angle \mathrm{ACE}\) అని రాసితిమి.
దీని మండి త్రిభుజము మూడు కోణాల మొత్తం రేఖీయ కోణముల మొత్తమునకు సమానమని చెప్పబడినది.

సోపానము 5 : “ఒక వస్తువుతో రెండు వస్తువులు సమానమైన, ఆ రెండు వస్తువులు సమానము” అను యూక్లిడ్ సామాన్యభావన ద్వారా మనము \(\angle \mathrm{ABC}+\angle \mathrm{BCA}+\angle \mathrm{CAB}=\angle \mathrm{DCE}+\angle \mathrm{BCA}+\angle \mathrm{ACE}\) = 180° అని చెప్పగలము. 2 మరియు 3 లో గల సిద్ధాంతాలను (విశ్లేషణ చేయకయే) నిరూపిద్దాం.

5. రెండు బేసి సంఖ్యల లబ్ధము బేసి సంఖ్య. (పేజీ నెం. 325)
సాధన.
నిరూపణ : x మరియు y రెండు బేసిసంఖ్యలు అనుకొనుము.
మనము xy ఒక బేసిసంఖ్య అని చూపాలి.
x, yలు బేసిసంఖ్యలు అయిన
x = (2m – 1), y = 2n – 1 (m, n లు ఏదైనా రెండు సహజసంఖ్యలు) గా రాయవచ్చు. అప్పుడు,
xy = (2m – 1) (2n – 1)
= 4mm – 2m – 2n + 1
= 4mm – 2m – 2n + 2 – 1
= 2(2m – m – n + 1) – 1
2mn – m – n + 1 – 1, lను ఏదేని సహజ సంఖ్యఅనుకొనిన
= 2l – 1, l ∈ N
ఇది కచ్చితంగా బేసి సంఖ్యయే.

6. రెండు వరుస సరిసంఖ్యల లబ్ధము 4చే భాగింపబడును. (పేజీ నెం. 326)
సాధన.
రెండు వరుస సరిసంఖ్యలు 2m, 2m + 2 (n ఏదైనా ఒక సహజసంఖ్య), వాటి లబ్దము 2m (2m + 2). 4ను భాగింపబడును అని నిరూపించాలి. (నిరూపణకు మీరు సొంతంగా ప్రయత్నించండి.)

ఉదాహరణలు :

1. ప్రధాన సంఖ్యల నిర్వచనము నుండి 3 ఒక ప్రధాన సంఖ్య అని చెప్పగలము. కావున ఇది ఒక ప్రవచనము. మిగిగిన వాక్యములలో ప్రవచనములలో గణిత పరంగా నిరూపించగలిగేవి ఏవి? (పేజీ నెం. 312)

2. రెండు బేసి సంఖ్యల లబ్దము ఒక సరిసంఖ్య. ఏవైన రెందు బేసి సంఖ్యలు 8, 5 తీసుకొనుము. వాటి లబ్దము 3 × 5 = 15 ఇది సరిసంఖ్యకాదు. (పేజీ నెం. 312)
సాధన.
ఈ ప్రవచన సత్య విలువ అసత్యము. కనుక ఒక ప్రత్యుదాహరణ ద్వారా మనము ఈ ప్రవచన సత్య విలువ నిర్ణయించగలము. ఒక ఉదాహరణ ద్వారా ఒక ప్రవచనం అసత్యము అని చెప్పవచ్చు. ఇటువంటి ఉదాహరణను ప్రత్యుదాహరణ అంటారు.

3. క్రింది వాక్యములను పరిశీలించండి. “భూమిని పరిపాలించుటకు మనుష్యులు కలరు”, “రాము ఒక మంచి డ్రైవర్”. (పేజీ నెం. 312)
సాధన.
ఈ వాక్యములు సందిగ్గదతో కూడి ఉన్న వాక్యములు. భూమిని పాలించుట అనునది కచ్చితముగా ఏ ప్రాంతము అనేది చెప్పబడలేదు. అదే విధముగా రెండవ వాక్యములో ఎటువంటి నైపుణ్యము మంచిదో అనేది స్పష్టంగా చెప్పబడలేదు. గణిత ప్రవచనములు కొన్ని పదాల కలయికతో, అందరికి స్పష్టంగా అర్థమగుతూ అది సత్యమో అసత్యమో నిర్ణయించగలిగేలా ఉండాలి.

4. భూమికి కల ఒకే ఒక ఉపగ్రహం చంద్రుడు. లీలావతి అను గ్రంథమును భాస్కరుడు రచించెను. ఈ వాక్యములు ప్రవచనములు అవునో కాదో ఎట్లు
నిర్ణయించగలవు? (పేజీ నెం. 312)
సాధన.
ఈ వాక్యములలో సందిగ్ధత లేదు, కాని కొంత నిరూపించవలసిన అవసరము కలదు. దీనిని నిర్ధారించుటకు పూర్వము నిరూపించబడిన అంశములపై సంబంధించిన అంశములు తెలిసి ఉండాలి, రెండవ వాక్యము కొరకు పుస్తక రచయితలు వాటికి సంబంధించిన అంశములు చారిత్రక గ్రంథములు తెలియవలెను.

5. కింది ప్రవచనములు షరతులకు లోబడి సరియగు సత్య ప్రవచనములు అగునట్లుగా తిరిగి రాయండి.

1. ప్రతి వాస్తవ సంఖ్య x కు 3x > x.
2. ప్రతి వాస్తవ సంఖ్య x కు x² ≥ x.
3. ఒక సంఖ్యను 2తో భాగించగా వచ్చిన సంఖ్య మొదటి సంఖ్యలో సగముండును.
4. ఒక వృత్తములో ఒక జ్యా వృత్తముపై ఏదైన ఒక బిందువు వద్ద ఏర్పరచు కోణము 90°.
5. ఒక చతుర్భుజంలో అన్ని భుజాలు సమానమైన అది ఒక చతురస్రము. (పేజీ నెం. 313)

సాధన.

1. x > 0 అయిన 3x >x.
2. x ≤ 0 లేదా x ≥ 1 అయిన x² ≥ x.
3. 0 తప్ప మిగిలిన సంఖ్యలను 2 తో భాగిస్తే వచ్చు సంఖ్య మొదటి సంఖ్యలో సగముండును.
4. ఒక వృత్తములో వృత్త వ్యాసము, వృత్తముపై ఏదైనా ఒక బిందువు వద్ద ఏర్పరచు కోణము 90°.
5. ఒక చతుర్భుజంలోని అన్ని భుజాలు, కోణాలు సమానమైన అది ఒక చతురస్రము.

6. కింది వరుసల చుక్కలు ఒక వరుస క్రమ సంఖ్యలను సూచిస్తుంది. (పేజీ నెం. 318)

(a) తరువాతి మూడు పదాలు కనుక్కోండి.
(b) 100వ పదము కనుక్కోండి.
(c) nవ పదము కనుక్కోండి.
ఇచ్చట కల సంఖ్యలు T₁ = 2, T₂ = 6, T₃ = 12, T₄ = 20 గా కలదు. T₅, T₆, T_n పదములను ఊహించగలరా ? T_n అను పదమును ఒక భావనగా తీసుకుందాం. పై విషయాన్ని తిరిగి ఇలా రాస్తే మనకు సాధనకు ఉపయోగపడవచ్చు.

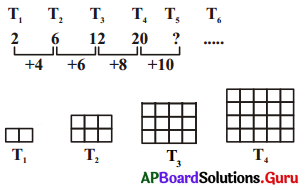
సాధన.
కావున T₅ = T₄ + 10 = 20 + 10 = 30 = 5 × 6
T₆ = T₅ + 12 = 30 + 12 = 42
= 6 × 7………. T₇ ఊహించండి,
T₁₀₀ = 100 × 101 = 10, 100
T_n = n × (n + 1) = n² + n