AP SCERT 9th Class Maths Textbook Solutions Chapter 13 జ్యామితీయ నిర్మాణాలు Ex 13.1 Textbook Exercise Questions and Answers.
AP State Syllabus 9th Class Maths Solutions 13th Lesson జ్యామితీయ నిర్మాణాలు Exercise 13.1
1. మూలబిందువు వద్ద దత్తకిరణంపై కింది కోణాలను నిర్మించి, నిరూపణ చేయండి.
ప్రశ్న (a)
90°
సాధన.

సోపానాలు :
→ \(\overrightarrow{\mathrm{AB}}\) ఇచ్చిన కిరణము అనుకొనుము.
→ BA ను D వరకు పొడిగించుము.
→ కొంత వ్యాసార్ధంతో A కేంద్రంగా ఒక అర్ధ వృత్తంను గీయుము.
→ X మరియు Y లు కేంద్రాలుగా రెండు ఖండన చాపాలను ఒకే వ్యాసార్ధంతో గీయుము.
→ చాపాల ఖండన బిందువును, ‘A’ ను కలుపుము.
→ \(\angle \mathrm{BAC}\) కావలసిన లంబకోణము.
(లేదా)
సోపానాలు :
→ \(\overrightarrow{\mathrm{AB}}\) ఇచ్చిన కిరణమనుకొనుము.
→ A కేంద్రంగా ఒక చాపంను గీయుము.
→ ముందుగా తీసుకున్న కొలతతో x కేంద్రంగా రెండు సమాన చాపాలను పటంలో చూపినట్లుగా గీయుము.
→ రెండు చాపాల ఖండన బిందువును, ‘A’ ను కలుపుము.
→ \(\angle \mathrm{BAC}\) = 90°
∆AXY లో \(\angle \mathrm{YAX}\) = 60° మరియు
∆AYC లో \(\angle \mathrm{YAC}\) = 30 ∴ \(\angle \mathrm{BAC}\) = 90°
![]()
ప్రశ్న (b)
45°
సాధన.
సోపానాలు :
→ ఇచ్చిన \(\overrightarrow{\mathrm{AB}}\) కిరణంతో 90° గీయుము.
→ \(\angle \mathrm{BAD}\) = 45° అగునట్లు ఈ కోణమును సమద్విఖండన చేయుము.
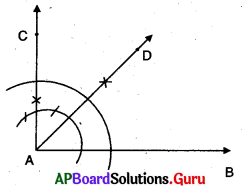
[లేదా]
[∆AXZ ఒక సమబాహు త్రిభుజము మరియు
\(\angle \mathrm{YAZ}\) = 15°
∴ \(\angle \mathrm{XAY}\) = 45°]
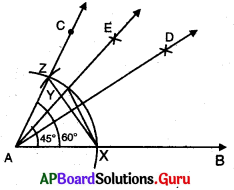
సోపానాలు :
→ \(\angle \mathrm{BAC}\) = 60° లను నిర్మించుము.
→ \(\angle \mathrm{BAC}\) ను \(\angle \mathrm{BAD}\) = \(\angle \mathrm{DAC}\) = 30° లగా సమద్విఖండన చేయుము.
→ \(\angle \mathrm{DAC}\) ను \(\angle \mathrm{DAE}\) = \(\angle \mathrm{EAC}\) = 15° అగునట్లుగా సమద్విఖండన చేయుము.
∴ \(\angle \mathrm{BAE}\) = 45°
2. కింది కోణాలను కొలబద్ద, వృత్తలేఖిని సహాయంతో నిర్మించి, కోణమానినితో కొలిచి సరిచూడండి.
ప్రశ్న (a)
30°
సాధన.
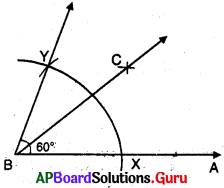
సోపానాలు :
→ \(\angle \mathrm{ABY}\) = 60° లను నిర్మించుము.
→ \(\angle \mathrm{ABC}\) = \(\angle \mathrm{CBY}\) = 30° అగునట్లు
\(\angle \mathrm{ABY}\) కు సమద్విఖండన రేఖను గీయుము.
![]()
ప్రశ్న (b)
22\(\frac {1}{2}\)°
సాధన.

సోపానాలు :
→ \(\angle \mathrm{ABD}\) = 90° లను నిర్మించుము.
→ \(\angle \mathrm{ABC}\) = \(\angle \mathrm{CBD}\) = 45° అగునట్లుగా \(\angle \mathrm{ABD}\) కు సమద్విఖండన రేఖను గీయుము.
→ \(\angle \mathrm{ABE}\) = \(\angle \mathrm{EBC}\) = 22\(\frac {1}{2}\)°, అగునట్లుగా \(\angle \mathrm{ABC}\) కు సమద్విఖండన రేఖను గీయుము.
ప్రశ్న (c)
15°
సాధన.
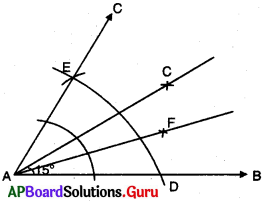
నిర్మాణ సోపానాలు :
→ \(\angle \mathrm{BAE}\) = 60° లను నిర్మించుము.
→ \(\angle \mathrm{BAC}\) = \(\angle \mathrm{CAE}\) = 30° అగునట్లుగా \(\angle \mathrm{BAE}\) కు సమద్విఖండన రేఖను గీయుము.
→ \(\angle \mathrm{BAF}\) = \(\angle \mathrm{FAC}\) = 15° అగునట్లుగా \(\angle \mathrm{BAC}\) కు సమద్విఖండన రేఖను గీయుము.
![]()
ప్రశ్న (d)
75°
సాధన.
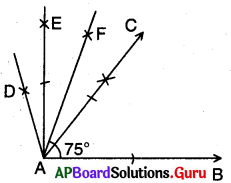
నిర్మాణ సోపానాలు :
→ \(\angle \mathrm{BAC}\) = 60° లను నిర్మించుము.
→ \(\angle \mathrm{CAD}\) = 60° లను నిర్మించుము.
→ \(\angle \mathrm{BAE}\) = 90° అగునట్లుగా \(\angle \mathrm{CAD}\) కు సమద్విఖండన రేఖను గీయుము.
→ \(\angle \mathrm{BAF}\) = 75° అగునట్లుగా \(\angle \mathrm{CAE}\) కు సమద్విఖండన రేఖను గీయుము.
ప్రశ్న (e)
105°
సాధన.
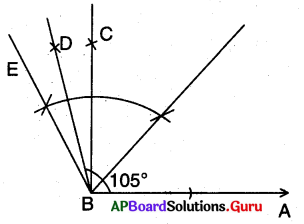
నిర్మాణ సోపానాలు :
→ \(\angle \mathrm{ABC}\) = 90° లను నిర్మించుము.
→ \(\angle \mathrm{CBE}\) = 30° లను నిర్మించుము.
→ \(\angle \mathrm{ABD}\) = 105° ఏర్పడునట్లుగా \(\angle \mathrm{CBE}\) కు సమద్విఖండన రేఖను గీయుము.
![]()
ప్రశ్న (f)
135°
సాధన.
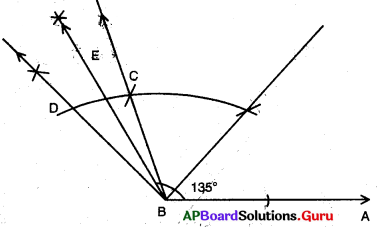
నిర్మాణ సోపానాలు:
→ \(\angle \mathrm{ABC}\) = 120° లను నిర్మించుము.
→ \(\angle \mathrm{CBD}\) = 30° లను నిర్మించుము.
→ \(\angle \mathrm{ABE}\) = 135° ఏర్పడునట్లుగా \(\angle \mathrm{CBD}\) కు సమద్విఖండన రేఖను గీయుము.
ప్రశ్న 3.
దత్త భుజం 4.5 సెం.మీ. తీసుకొని ఒక సమబాహు త్రిభుజం నిర్మించి, నిర్మాణాన్ని నిరూపించండి.
సాధన.
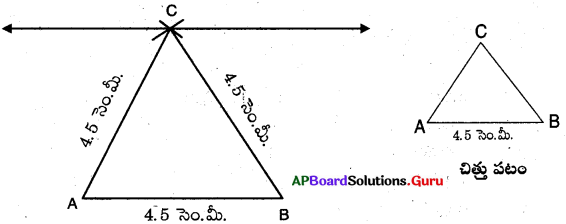
నిర్మాణ సోపానాలు :
→ AB = 4.5 సెం.మీ.లతో రేఖాఖండంను గీయుము.
→ 4.5 సెం.మీ.ల వ్యాసార్థంతో A మరియు B.లు కేంద్రంగా చాపములను గీయుము. అవి C వద్ద ఖండించుకొనును.
→ A, C లను మరియు B, C లను కలుపుము.
→ మనకు కావలసిన ∆ABC ఏర్పడినది.
నిరూపణ :
∆ABC లో AB = AC ⇒ \(\angle \mathrm{C}=\angle \mathrm{B}\)
అదే విధంగా AB = BC ⇒ \(\angle \mathrm{C}=\angle \mathrm{A}\)
∴ \(\angle \mathrm{A}=\angle \mathrm{B}=\angle \mathrm{C}\)
కాని \(\angle \mathrm{A}+\angle \mathrm{B}+\angle \mathrm{C}\) = 180°
∴ \(\angle \mathrm{A}=\angle \mathrm{B}=\angle \mathrm{C}\) = \(\frac {180°}{3}\) = 60°
![]()
ప్రశ్న 4.
దత్తభుజంను భూమిగా తీసుకొని, దత్తకోణం తెలిస్తే సమద్విబాహు త్రిభుజం నిర్మించి, నిర్మాణాన్ని నిరూపించండి. [సూచన : నిర్మాణాలకు మీకు నచ్చిన భుజం కొలత, కోణం కొలత తీసుకోవచ్చు)
సాధన.
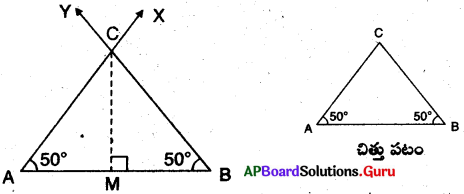
నిర్మాణ సోపానాలు :
→ ఏదైనా ఇచ్చిన కొలతతో AB రేఖాఖండమును గీయుము.
→ \(\angle \mathrm{BAX}\) మరియు \(\angle \mathrm{ABY}\)ల వద్ద \(\angle \mathrm{A}=\angle \mathrm{B}\) అగునట్లుగా A మరియు B లను గీయుము.
→ \(\overrightarrow{\mathrm{AX}}\) మరియు \(\overrightarrow{\mathrm{BY}}\) లను పొడిగించగా అవి C వద్ద ఖండించుకొనును.
→ ∆ABC కావలసిన త్రిభుజము.
నిరూపణ:
→ AB కు లంబంగా C నుండి ఒక లంబము CM ను గీయుము.
∆AMC మరియు ∆BMC లలో
\(\angle \mathrm{AMC}=\angle \mathrm{BMC}\) (∵ లంబకోణము)
\(\angle \mathrm{A}=\angle \mathrm{B}\) (∵నిర్మాణము)
CM = CM (ఉమ్మడి భుజము)
∴ ∆AMC ≅ ∆BMC
⇒ AC = BC [CPCT]