AP Board 9th Class Maths Solutions Chapter 12 Circles Ex 12.4

AP State Syllabus AP Board 9th Class Maths Solutions Chapter 12 Circles Ex 12.4 Textbook Questions and Answers.

AP State Syllabus 9th Class Maths Solutions 12th Lesson Circles Exercise 12.4

Question 1.
In the figure, ‘O’ is the centre of the circle. ∠AOB = 100°, find ∠ADB.

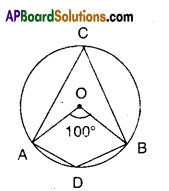
Solution:
’O’ is the centre
∠AOB = 100°

Thus ∠ACB = \(\frac{1}{2}\) ∠AOB
[∵ angle made by an arc at the centre is twice the angle made by it on the remaining part]]
= \(\frac{1}{2}\) x 100° = 50°
∠ACB and ∠ADB are supplementary
[ ∵ Opp. angles of a cyclic quadrilateral]
∴ ∠ADB = 180°-50° = 130°
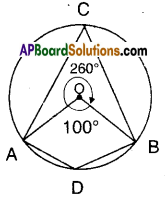
[OR]
∠ADB is the angle made by the major arc \(\widehat{\mathrm{ACB}}\) at D.
∴ ∠ADB = \(\frac{1}{2}\)∠AOB [where ∠AOB is the angle; made by \(\widehat{\mathrm{ACB}}\) at the centre]
= \(\frac{1}{2}\) [360° – 100°] [from the figure]
= \(\frac{1}{2}\) x 260° = 130°

Question 2.
In the figure, ∠BAD = 40° then find ∠BCD.

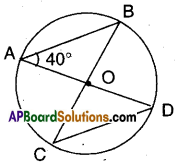
Solution:
‘O’ is the centre of the circle.
∴ In ΔOAB; OA = OB (radii)
∴ ∠OAB = ∠OBA = 40°
(∵ angles opp. to equal sides)
Now ∠AOB = 180° – (40° + 40°)
(∵ angle sum property of ΔOAB)
= 180°-80° = 100°
But ∠AOB = ∠COD = 100°
Also ∠OCD = ∠ODC [OC = OD]
= 40° as in ΔOAB
∴ ∠BCD = 40°
(OR)
In ΔOAB and ΔOCD
OA = OD (radii)
OB = OC (radii)
∠AOB = ∠COD (vertically opp. angles)
∴ ΔOAB ≅ ΔOCD
∴ ∠BCD = ∠OBA = 40°
[ ∵ OB = OA ⇒ ∠DAB = ∠DBA]

Question 3.
In the figure, ‘O’ is the centre of the circle and ∠POR = 120°. Find ∠PQR and ∠PSR.

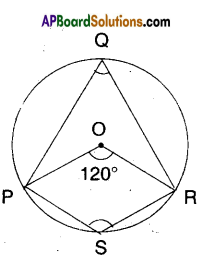
Solution:
‘O’ is the centre; ∠POR = 120°
∠PQR = \(\frac{1}{2}\)∠POR [∵ angle made by an arc at the centre is, twice the angle made by it on the remaining part]
∠PSR = \(\frac{1}{2}\) [Angle made by \(\widehat{\mathrm{PQR}}\) at the centre]
∠PSR = \(\frac{1}{2}\) [360° – 120°] from the fig.
= \(\frac{1}{2}\) x 240 = 120°

Question 4.
If a parallelogram is cyclic, then it is a rectangle. Justify.
Solution:

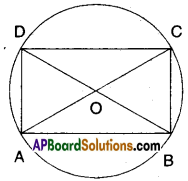
Let □ABCD be a parallelogram such
that A, B, C and D lie on the circle.
∴∠A + ∠C = 180° and ∠B + ∠D = 180°
[Opp. angles of a cyclic quadri lateral are supplementary]
But ∠A = ∠C and ∠B = ∠D
[∵ Opp. angles of a ||gm are equal]
∴∠A = ∠C =∠B =∠D = \(\frac{180}{2}\) = 90°
Hence □ABCD is a rectangle

Question 5.
In the figure, ‘O’ is the centr of the circle. 0M = 3 cm and AB = 8 cm. Find the radius of the circle.

Solution:

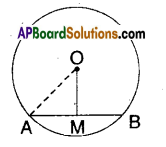
‘O’ is the centre of the circle.
OM bisects AB.
∴ AM = \(\frac{\mathrm{AB}}{2}=\frac{8}{2}\) = 4 cm
OA² = OM² + AM² [ ∵ Pythagoras theorem]
OA \(\begin{array}{l}
=\sqrt{3^{2}+4^{2}} \\
=\sqrt{9+16}=\sqrt{25}
\end{array}\)
= 5cm

Question 6.
In the figure, ‘O’ is the centre of the circle and OM, ON are the perpen-diculars from the centre to the chords PQ and RS. If OM = ON and PQ = 6 cm. Find RS.

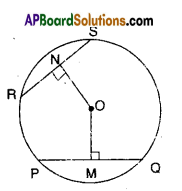
Solution:
‘O’ is the centre of the circle.
OM = ON and 0M ⊥ PQ; ON ⊥ RS
Thus the chords FQ and RS are equal.
[ ∵ chords which are equidistant from the centre are equal in length]
∴ RS = PQ = 6cm

Question 7.
A is the centre of the circle and ABCD is a square. If BD = 4 cm then find the
radius of the circle.

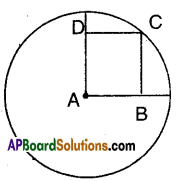
Solution:

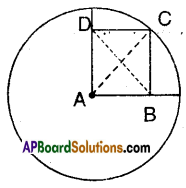
A is the centre of the circle and ABCD is a square, then AC and BD are its diagonals. Also AC = BD = 4 cm But AC is the radius of the circle.
∴ Radius = 4 cm.

Question 8.
Draw a circle with any radius and then draw two chords equidistant
from the centre.
Solution:

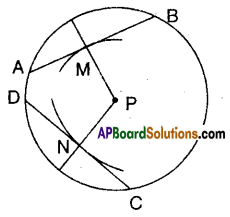
1. Draw a circle with centre P.
2. Draw any two radii.
3. Mark off two points M and N oh these radii. Such that PM = PN.
4. Draw perpendicular through M and N to these radii.

Question 9.
In the given figure, ‘O’ is the centre of the circle and AB, CD are equal chords. If ∠AOB = 70°. Find the angles of ΔOCD.

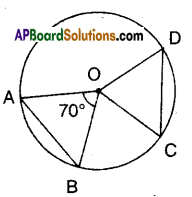
Solution:
‘O’ is the centre of the circle.
AB, CD are equal chords
⇒ They subtend equal angles at the centre.
∴ ∠AOB =∠COD = 70°
Now in ΔOCD
∠OCD = ∠ODC [∵ OC = OD; radii angles opp. to equal sides]
∴ ∠OCD + ∠ODC + 70° = 180°
= ∠OCD +∠ODC = 180° – 70° = 110°
∴ ∠OCD + ∠ODC = 110° = 55°