AP SCERT 9th Class Maths Textbook Solutions Chapter 12 వృత్తాలు Ex 12.3 Textbook Exercise Questions and Answers.
AP State Syllabus 9th Class Maths Solutions 12th Lesson వృత్తాలు Exercise 12.3
1. కింది త్రిభుజాలను గీచి వాటికి పరిషృత్తాలను నిర్మించండి.
ప్రశ్న (i)
∆ABC లో AB = 6 సెం.మీ., BC = 7 సెం.మీ., మరియు \(\angle \mathbf{A}\) = 60°.
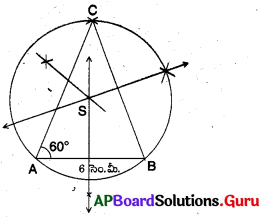
సాధన.
నిర్మాణ సోపానాలు :
→ ఇచ్చిన కొలతలతో త్రిభుజంను నిర్మించుము.
→ భుజాలకు లంబసమద్విఖండన రేఖలను గీయుము.
→ లంబ సమద్విఖండన రేఖల మిళిత బిందువు ‘S’.
→ S కేంద్రముగా; SA వ్యాసార్ధంగా తీసుకొని ఒక వృత్తంను గీయుము. అది B మరియు C ల గుండా పోవును.
→ ఇదియే మనకు కావలసిన పరివృత్తము.
![]()
ప్రశ్న (ii)
∆PQR లో PQ = 5 సెం.మీ., QR = 6 సెం.మీ. మరియు RP = 8.2 సెం.మీ.
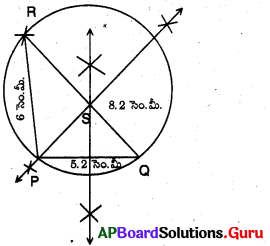
సాధన.
నిర్మాణ సోపానాలు :
→ ఇచ్చిన కొలతలతో ∆PQR ను నిర్మించుము.
→ PQ, QR మరియు RSలకు లంబసమద్విఖండన రేఖలను గీసిన అవి ‘S’ వద్ద ఖండించుకొనును.
→ S కేంద్రముగా SP వ్యాసార్ధంతో వృత్తంను గీయుము.
→ ఈ వృత్తం మిగిలిన శీర్షాల గుండా పోవును.
→ ఇదియే మనకు కావలసిన పరివృత్త త్రిభుజం.
ప్రశ్న (iii)
∆XYZ లో XY = 4.8 సెం.మీ., \(\angle \mathbf{X}\) = 60° మరియు \(\angle \mathbf{Y}\) = 70°.
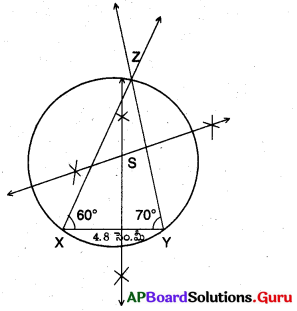
సాధన.
నిర్మాణ సోపానాలు :
→ ఇచ్చిన కొలతలతో, ∆XYZ ను గీయుము.
→ ∆XYZ యొక్క భుజాలు XY, YZ, ZX లకు లంబసమద్విఖండన రేఖలను గీయుము. ఇవి ఖండించుకొను బిందువును ‘S’ అనుకొనుము.
→ ‘S’ కేంద్రంగా \(\overline{\mathrm{SX}}\) వ్యాసార్ధంతో ఒక వృత్తంను గీయుము. అది Y మరియు Z లను తాకుతూ పోవును.
→ ఇదియే మనకు కావలసిన పరివృత్తము.
![]()
ప్రశ్న 2.
AB = 5.4 సెం.మీ. గీచి A, B ల గుండా పోయే రెండు వృత్తాలను గీయండి.
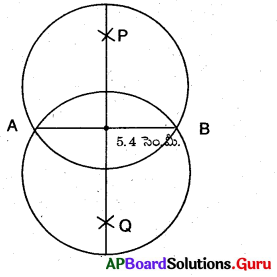
సాధన.
నిర్మాణ సోపానాలు :
→ AB = 5.4 సెం.మీ.లతో ఒక రేఖా ఖండంను గీయుము.
→ ABకు లంబంగా \(\stackrel{\leftrightarrow}{XY}\) అను లంబ సమద్విఖండన రేఖను గీయుము.
→ XY పై ఏదైనా ఒక బిందువు P ను తీసుకొనుము.
→ P కేంద్రంగా PA వ్యాసార్థంతో ఒక వృత్తంను గీయుము.
→ XY పై మరొక బిందువు Q అనుకొనుము.
→ ‘Q’ కేంద్రంగా \(\overline{\mathrm{QA}}\) వ్యాసార్ధంతో మరొక వృత్తమును గీయుము.
ప్రశ్న 3.
రెండు వృత్తాలు రెండు వేర్వేరు బిందువుల వద్ద ఖండించుకుంటే వాటి కేంద్రాలు ఉమ్మడి జ్యా యొక్క లంబసమద్విఖండన రేఖపై ఉంటాయని నిరూపించండి.
సాధన.
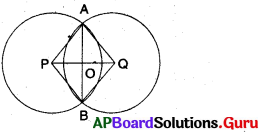
P మరియు Qలు కేంద్రాలుగా గల రెండు వృత్తాలు A మరియు B అను రెండు వేర్వేరు బిందువుల వద్ద ఖండించుకొనుచున్నవి.
A, B లను కలుపగా \(\overline{\mathrm{AB}}\) అను ఉమ్మడి జ్యా ఏర్పడినది.
‘O’, P, Qల మధ్య బిందువు.
OP, OQ లను కలుపుము.
ΔAPO మరియు ΔBPO లలో
AP = BP (వ్యాసార్ధాలు)
PO = PO (ఉమ్మడి భుజము)
AO = BO (∵ O మధ్య బిందువు)
∴ ΔAPO ≅ ΔBPO (భు.భు.భు. నియమం ప్రకారం)
⇒ \(\angle \mathrm{AOP}=\angle \mathrm{BOP}\) [C.P.C.T]
కాని ఇవి రేఖీయ ద్వయాలు కావున
∴ \(\angle \mathrm{AOP}=\angle \mathrm{BOP}\) = 90°
అదే విధముగా ΔAOQ మరియు ΔBOQ లలో
AQ = BQ (వ్యాసార్ధాలు)
AO = BO (∵ AB మధ్య బిందువు O)
OQ = OQ (ఉమ్మడి భుజం)
∴ ΔAOQ ≅ ΔBOQ
\(\angle \mathrm{AOQ}=\angle \mathrm{BOQ}\) (C.P.C.T)
మరియు \(\angle \mathrm{AOQ}=\angle \mathrm{BOQ}\) = 180° (రేఖీయద్వయం)
∴ \(\angle \mathrm{AOQ}=\angle \mathrm{BOQ}\) = \(\frac {180°}{2}\) = 90° ఇప్పుడు \(\angle \mathrm{AOP}=\angle \mathrm{AOQ}\) = 180°
∴ PQ ఒక రేఖ
![]()
ప్రశ్న 4.
ఒక వృత్తంలో ఖండించుకొనుచున్న రెండు జ్యాలు వాటి అందన బిందువు ద్వారా పోయే వ్యాసంతో సమాన కోణాలు చేస్తే ఆ జ్యాల పొడవులు సమానమని నిరూపించండి.
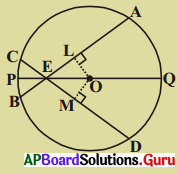
సాధన.
‘O’ వృత్త కేంద్రమనుకొనుము
PQ వృత్తవ్యాసము
\(\overline{\mathrm{AB}}\) మరియు \(\overline{\mathrm{CD}}\) అను రెండు జ్యాలు ‘E’ అను బిందువు వద్ద ఖండించుకొనుచున్నవి.
‘E’ వ్యాసముపై గల బిందువు.
\(\angle \mathrm{AEO}=\angle \mathrm{DEO}\)
AB మరియు CD ల పైకి ‘O’ నుండి OL మరియు
OM అను లంబాలను గీయుము.
∆LEO మరియు ∆MEOలలో
\(\angle \mathrm{LEO}=\angle \mathrm{MEO}\) (దత్తాంశం నుండి)
EO = EO (ఉమ్మడి భుజము)
\(\angle \mathrm{ELO}=\angle \mathrm{EMO}\) = 90° (నిర్మాణం నుండి)
∴ ∆LEO ≅ ∆MEO (∵ కో.భు. కో. నియమం ప్రకారం)
∴ OL = OM [C.P.C.T]
అదే విధముగా కేంద్రము ‘O’ నుండి \(\overline{\mathrm{AB}}\) మరియు \(\overline{\mathrm{CD}}\) లు సమాన దూరంలో గల రెండు జ్యాలు.
∴ AB = CD (∵ కేంద్రం నుండి సమాన దూరంలో గల జ్యాలు) నిరూపించబడినది.
ప్రశ్న 5.
కింది పటంలో ‘O’ కేంద్రంగా గల వృత్తంలో AB ఒక జ్యా CD వ్యాసం AB కు లంబంగా ఉంది. అయిన AD = BD అని చూపండి.
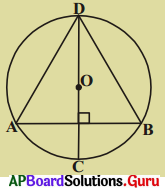
సాధన.
CD వృత్త వ్యాసము మరియు O వృత్త కేంద్రము.
CD ⊥ AB; M ఖండన బిందువనుకొనుము.
∆AMD మరియు ∆BMD లలో
AM = BM (∵ వృత్తంలోని జ్యాను, వృత్త వ్యాసార్ధం సమద్విఖండన చేయును)
\(\angle \mathrm{AMD}=\angle \mathrm{BMD}\) (∵ దత్తాంశము)
DM = DM (ఉమ్మడి భుజం)
∴ ∆AMD ≅ ∆BMD
⇒ AD = BD [C.P.C.T]