AP Board 9th Class Maths Solutions Chapter 12 Circles Ex 12.3

AP State Syllabus AP Board 9th Class Maths Solutions Chapter 12 Circles Ex 12.3 Textbook Questions and Answers.

AP State Syllabus 9th Class Maths Solutions 12th Lesson Circles Exercise 12.3

Question 1.
Draw the following triangles and construct circumcircles for them.
(OR)
In ΔABC, AB = 6 cm, BC = 7 cm and ∠A = 60°.
Construct a circumcircle to the triangle XYZ given XY = 6cm, YZ = 7cm and ∠Y = 60°. Also, write steps of construction.
Solution:

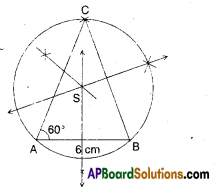
Steps of construction :

1. Draw the triangle with given mea-sures.
2. Draw perpendicular bisectors to the sides.
3. The point of concurrence of per-pendicular bisectors be S’.
4. With centre S; SA as radius, draw a circle which also passes through B and C.
5. This is the required circumcircle.

ii) In ΔPQR; PQ = 5 cm, QR = 6 cm and RP = 8.2 cm.

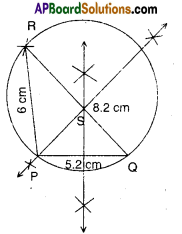
Steps of construction:

1. Draw ΔPQR with given measures.
2. Draw perpendicular to PQ, QR and RS; let they meet at ‘S’.
3. With S as centre and SP as radius draw a circle.
4. This is the required circumcircle.

iii) In ΔXYZ, XY = 4.8 cm, ∠X = 60°and ∠Y = 70°.

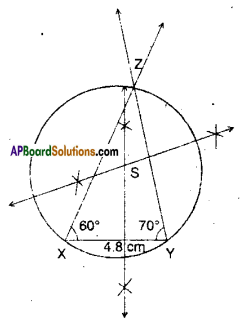
Steps of construction:

1. Draw ΔXYZ with given measures.
2. Draw perpendicular bisectors to the sides of ΔXYZ, let the point of con-currence be S’.
3. Draw the circle (S, \(\overline{\mathrm{SX}}\)).
4. This is the required circumcircle.

Question 2.
Draw two circles passing A, B where AB = 5.4 cm.
(OR)
Draw a line segment AB with 5.4 cm. length and draw two different circles that passes through both A and B.
Solution:

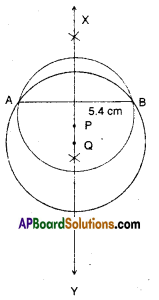
Steps of construction:

1. Draw a line segment AB = 5.4 cm.
2. Draw the perpendicular bisector \(\stackrel{\leftrightarrow}{X Y}\) of AB.
3. Take any point P on \(\stackrel{\leftrightarrow}{X Y}\).
4. With P as centre and PA as radius draw a circle.
5. Let Q be another point on XY.
6. Draw the circle (Q, \(\overline{\mathrm{QA}}\)).

Question 3.
If two circles intersect at two points, then prove that their centres lie on the perpendicular bisector of the common chord.
Solution:

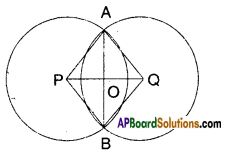
Let two circles with centre P and Q intersect at two distinct points say A and B.
Join A, B to form the common chord
\(\overline{\mathrm{AB}}\). Let ‘O’ be the midpoint of AB.
Join ‘O’ with P and Q.
Now in ΔAPO and ΔBPO
AP = BP (radii)
PO = PO (common)
AO = BO (∵ O is the midpoint)
∴ ΔAPO ≅ ΔBPO (S.S.S. congruence)
Also ∠AOP = ∠BOP (CPCT)
But these are linear pair of angles.
∴ ∠AOP = ∠BOP = 90°
Similarly in ΔAOQ and ΔBOQ
AQ = BQ (radii)
AO = BO (∵ O is the midpoint of AB)
OQ = OQ (common)
∴ AAOQ ≅ ABOQ
Also ∠AOQ = ∠BOQ (CPCT)
Also ∠AOQ + ∠BOQ = 180° (linear pair of angles)
∴ ∠AOQ = ∠BOQ = \(\frac{180^{\circ}}{2}\) = 90°
Now ∠AOP + ∠AOQ = 180°
∴ PQ is a line.
Hence the proof.

Question 4.
If two intersecting chords of a circle make equal angles with diameter pass¬ing through their point of intersection, prove that the chords are equal.

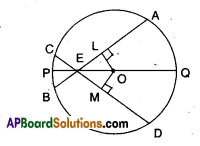
Solution:
Let ‘O’ be the centre of the circle.
PQ is a drametre.
\(\overline{\mathrm{AB}}\) and \(\overline{\mathrm{CD}}\) are two chords meeting at E, a point on the diameter.
∠AEO = ∠DEO
Drop two perpendiculars OL and OM from ‘O’ to AB and CD;
Now in ΔLEO and ΔMEO
∠LEO = ∠MEO [given]
EO = EO [Common]
∠ELO = ∠EMO [construction 90°]
∴ ΔLEO ≅ ΔMEO
[ ∵ A.A.S. congruence]
∴ OL = OM [CPCT]
i.e., The two chords \(\overline{\mathrm{AB}}\) and \(\overline{\mathrm{CD}}\) are at equidistant from the centre ‘O’.
∴ AB = CD
[∵ Chords which are equi-distant from the centre are equal]
Hence proved.

Question 5.
In the given figure, AB is a chord of circle with centre ‘O’. CD is the diam-eter perpendicular to AB. Show that AD = BD.

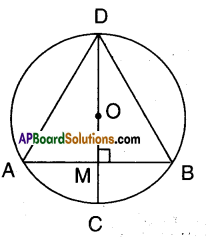
Solution:
CD is diameter, O is the centre.
CD ⊥ AB; Let M be the point of inter-section.
Now in ΔAMD and ΔBMD
AM = BM [ ∵ radius perpendicular to a chord bisects it]
∠AMD =∠BMD [given]
DM = DM (common)
∴ ΔAMD ≅ ΔBMD
⇒ AD = BD [C.P.C.T]