AP Board 9th Class Maths Solutions Chapter 1 వాస్తవ సంఖ్యలు InText Questions

SCERT AP 9th Class Maths Solutions Chapter 1 వాస్తవ సంఖ్యలు InText Questions and Answers.

AP State Syllabus 9th Class Maths Solutions 1st Lesson వాస్తవ సంఖ్యలు InText Questions

ఇవి చేయండి

1. [latex]\frac {-3}{4}[/latex] ను సంఖ్యారేఖపై సూచించండి. (పేజీ నెం. 3)
సాధన.

సోపానం – 1: -2, -1, 0, 1, 2 లను సూచిస్తూ ఒక సంఖ్యారేఖ, గీయండి.
సోపానం – 2: ‘0’ కు ఎడమవైపు ప్రతి యూనిట్ ను నాలుగు సమాన భాగాలుగా చేయండి. ఇందు నుంచి 3 భాగాలను తీసుకోండి.
సోపానం – 3: సున్నా నుండి ఎడమవైపు గల 3వ బిందువు [latex]\frac {-3}{4}[/latex] ను సూచిస్తుంది.

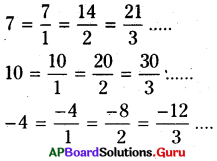
2. 0, 7, 10, – 4 లను [latex]\frac{p}{q}[/latex] రూపంలో వ్రాయండి. (పేజీ నెం. 3)
సాధన.
0 = [latex]\frac{0}{2}[/latex]

3. నేననుకున్న సంఖ్యను చెప్పండి : మీ స్నేహితుడు 10 నుండి 100 మధ్యలో ఒక సంఖ్యను మనసులో అనుకున్నాడు. అతడనుకున్న సంఖ్యను నీవు అతి తక్కువ ప్రశ్నలడుగుతూ ఎలా రాబట్టగలవు? నీవడిగిన ప్రశ్నలకు మీ స్నేహితుడు కేవలం ‘అవును’ లేదా ‘కాదు’ అని మాత్రమే సమాధానమిస్తాడు. (పేజీ నెం. 3)
సాధన.
నా స్నేహితుడు 73 ను తీసుకున్నాడు అనుకొనుము. అతనిని అడిగిన ప్రశ్నల సరళావళి ఈ విధముగా కలదు.

ప్రశ్న : ఆ సంఖ్య మొదటి 50 సంఖ్యలలో కలదా ?
జ. కాదు.

ప్రశ్న : ఒకవేళ ఆ సంఖ్య 50, 60 ల మధ్యన కలదా ?
జ. కాదు.

ప్రశ్న : ఒకవేళ ఆ సంఖ్య 60, 70 ల మధ్యన కలదా ?
జ. కాదు.

ప్రశ్న : ఒకవేళ ఆ సంఖ్య 70, 80ల మధ్యన కలదా ?
జ. అవును.

ప్రశ్న : ఆ సంఖ్య ఏదైనా ప్రధాన సంఖ్యా ?
జ. అవును. (నా ఆలోచన :70, 80 ల మధ్యన 71, 73 లేక 79లు మాత్రమే ప్రధాన సంఖ్యలు కదా !)

ప్రశ్న : ఒకవేళ ఆ సంఖ్య 75 కన్నా చిన్న సంఖ్యేనా ?
జ. అవును. (నా ఆలోచన : అంటే ఆ సంఖ్య 71 లేక 73 అయి వుండాలి.)

ప్రశ్న : ఆ సంఖ్య 72 కన్నా చిన్నదేనా ?
జ. కాదు
∴ ఆ సంఖ్య 73. ఈ విధముగా మనము సంఖ్యా ధర్మా లైన/ రకాలైన సరి, బేసి, ప్రధాన, సంయుక్త మొ॥ వాటిని అనుసరించి ఈ రకపు సమస్యలను సాధించవచ్చును.

4. i) 2, 3 ల మధ్య సగటు పద్ధతి ద్వారా ఐదు అకరణీయ సంఖ్యలుంచండి. (పేజీ నెం. 4)
సాధన.
a మరియు b ల మధ్య [latex]\frac{a+b}{2}[/latex] అను అకరణీయ సంఖ్య గలదు.
a = 2 మరియు b = 3 అనుకొనుము.
[latex]\frac{a+b}{2}=\frac{2+3}{2}=\frac{5}{2}[/latex]
∴ 2 < [latex]\frac{5}{2}[/latex] < 3
ఈ పద్ధతిని కొనసాగిస్తే మనం 2 మరియు 3 ల మధ్య మరికొన్ని అకరణీయ సంఖ్యలను ఉంచవచ్చును.

ii) [latex]\frac {-3}{11}[/latex] మరియు [latex]\frac {8}{11}[/latex] ల మధ్య పది ఆకరణీయ సంఖ్యలుంచండి. (పేజీ నెం. 4)
సాధన.

5. i) [latex]\frac{1}{17}[/latex] ను దశాంశ రూపంలో రాయండి. (పేజీ నెం. 5)
సాధన.

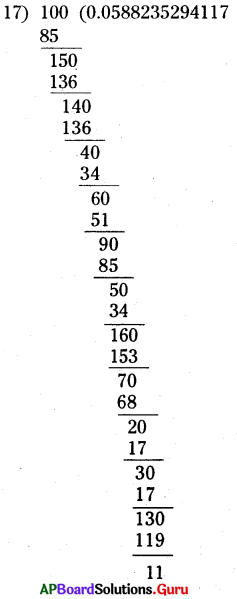
[latex]\frac{1}{17}[/latex] = 0.0588235294117 ……..

ii) [latex]\frac{1}{19}[/latex]ను దశాంశ రూపంలో రాయండి. (పేజీ నెం. 5)
సాధన.

[latex]\frac{1}{19}[/latex] = 0.052631578………

6. కింది సంఖ్యల హారాలకు అకరణీయ కారణాంకాలు కనుగొనుము. (పేజీ నెం. 20)
i) [latex]\frac{1}{2 \sqrt{3}}[/latex]
సాధన.
[latex]\frac{1}{2 \sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}}=\frac{\sqrt{3}}{2 \times 3}=\frac{\sqrt{3}}{6}[/latex]
∴ [latex]\sqrt{3}[/latex] యొక్క అకరణీయ కారణాంకము [latex]\sqrt{3}[/latex].

ii) [latex]\frac{3}{\sqrt{5}}[/latex]
సాధన.
[latex]\frac{3}{\sqrt{5}} \times \frac{\sqrt{5}}{\sqrt{5}}=\frac{3 \sqrt{5}}{5}[/latex]
∴ [latex]\sqrt{5}[/latex] యొక్క అకరణీయ కారణాంకము [latex]\sqrt{5}[/latex]

iii) [latex]\frac{1}{\sqrt{8}}[/latex]
సాధన.

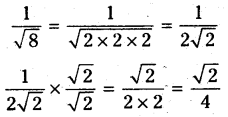
∴ [latex]\sqrt{2}[/latex] యొక్క అకరణీయ కారణాంకము [latex]\sqrt{2}[/latex]

7. సూక్ష్మీకరించండి. (పేజీ నెం. 23)
i) (16)^1/2
సాధన.
(4 × 4)^1/2 = (4²)^1/2 = 4^2/2 = 4

ii) (128)^1/7
సాధన.
(128)^1/7 = (2 × 2 × 2 × 2 × 2 × 2 × 2)^1/7
=(2⁷)^1/7 = 2

iii) (343)^1/5
సాధన.
(343)^1/5 = (3 × 3 × 3 × 3 × 3)^1/5 = (3⁵)^1/5 = 3

8. కింది కరణులను ఘాతరూపంలో రాయండి. (పేజీ నెం. 24)
i) [latex]\sqrt{2}[/latex]
సాధన.
[latex]\sqrt{2}[/latex] = [latex]2^{\frac{1}{2}}[/latex]

ii) [latex]\sqrt[3]{9}[/latex]
సాధన.
[latex]\sqrt[3]{9}=\sqrt[3]{3 \times 3}[/latex]
= [latex]\sqrt[3]{3^{2}}=3^{\frac{2}{3}}[/latex]

iii) [latex]\sqrt[5]{20}[/latex]
సాధన.
[latex]\sqrt[5]{20}[/latex] = [latex]\sqrt[5]{2 \times 2 \times 5}=\sqrt[5]{2^{2} \times 5}[/latex]
= [latex]2^{\frac{2}{5}} \times 5^{\frac{1}{5}}[/latex]

iv) [latex]\sqrt[17]{19}[/latex]
సాధన.
[latex]\sqrt[17]{19}[/latex] = [latex]19^{\frac{1}{17}}[/latex]

9. కింది కరణులను రాడికల్ రూపంలో రాయండి. (పేజీ నెం. 24)
i) [latex]5^{1 / 7}[/latex]
ii) [latex]17^{1 / 6}[/latex]
iii) [latex]5^{2 / 5}[/latex]
iv) [latex]142^{1 / 2}[/latex]
సాధన.
i) [latex]5^{1 / 7}[/latex] = [latex]\sqrt[7]{5}[/latex]
ii) [latex]17^{1 / 6}[/latex] = [latex]\sqrt[6]{17}[/latex]
iii) [latex]5^{2 / 5}[/latex] = [latex]\sqrt[5]{5^{2}}=\sqrt[5]{5 \times 5}=\sqrt[5]{25}[/latex]
iv) [latex]142^{1 / 2}[/latex] = [latex]\sqrt{142}[/latex]

ప్రయత్నించండి

1. కింది సంఖ్యల దశాంశ విలువలను కనుగొనండి. (పేజీ నెం. 6)
i) [latex]\frac{1}{2}[/latex]
ii) [latex]\frac{1}{2^{2}}[/latex]
iii) [latex]\frac{1}{5}[/latex]
iv) [latex]\frac{1}{5 \times 2}[/latex]
v) [latex]\frac{3}{10}[/latex]
vi) [latex]\frac{27}{25}[/latex]
vii) [latex]\frac{1}{3}[/latex]
viii) [latex]\frac{7}{6}[/latex]
ix) [latex]\frac{5}{12}[/latex]
x) [latex]\frac{1}{7}[/latex]
సాధన.
i) [latex]\frac{1}{2}[/latex] = 0.5
ii) [latex]\frac{1}{2^{2}}[/latex] = [latex]\frac{1}{4}[/latex] = 0.25
iii) [latex]\frac{1}{5}[/latex] = 0.2
iv) [latex]\frac{1}{5 \times 2}[/latex] = [latex]\frac{1}{10}[/latex] = 0.1
v) [latex]\frac{3}{10}[/latex] = 0.3

vi) [latex]\frac{27}{25}[/latex]

vii) [latex]\frac{1}{3}[/latex]

viii) [latex]\frac{7}{6}[/latex]

ix) [latex]\frac{5}{12}[/latex]

x) [latex]\frac{1}{7}[/latex]

2. [latex]\sqrt{3}[/latex] యొక్క విలువను ఆరు దశాంశ స్థానాల వరకు భాగహార పద్ధతిలో కనుక్కోండి. (పేజీ నెం. 10)
సాధన.

సోపానం-1 : 3 తర్వాత దశాంశ బిందువుని ఉంచుము.
3.00 00 00 00 00 00 00
సోపానం-2 : దశాంశ బిందువు తరువాత ‘0’ లు రాయుము.
సోపానం-3 : ‘0’ లను జతలుగా చేసి పైన బార్‌ను గీయుము.
సోపానం-4 : పిదప సంపూర్ణ వర్గము కనుగొను పద్ధతిని అనుకరించుము.
∴ [latex]\sqrt{3}[/latex] = 1.732050

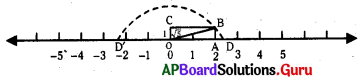
3. [latex]\sqrt{5}[/latex] మరియు -[latex]\sqrt{5}[/latex] లను సంఖ్యారేఖపై సూచించండి. (పేజీ నెం. 12)
(సూచన : 5 = 2² + 1²)
సాధన.
సోపానం-1 : 2 యూనిట్ల పొడవు, ఒక యూనిట్ వెడల్పుగా గల ఒక దీర్ఘచతురస్రం OABC ను సున్నా వద్ద గీయుము.
సోపానం-2 : ఆ దీర్ఘచతురస్ర కర్ణము
OB = [latex]\sqrt{\mathrm{OA}^{2}+\mathrm{AB}^{2}}[/latex]
= [latex]\sqrt{2^{2}+1^{2}}[/latex] = [latex]\sqrt{4+1}[/latex] = [latex]\sqrt{5}[/latex]
సోపానం-3 : ఒక వృత్తలేఖినిని ఉపయోగించి ‘O’ కేంద్రముగా OB వ్యాసార్ధంతో సంఖ్యారేఖ పై ‘O’ కు ఇరువైపులా చాపములను గీయగా అవి సంఖ్యారేఖ పై D మరియు D’ల వద్ద ఖండించుచున్నవి.
సోపానం-4 : సంఖ్యారేఖపై D విలువ [latex]\sqrt{5}[/latex] ను మరియు D’ విలువ -[latex]\sqrt{5}[/latex] ను సూచిస్తుంది.

ఆలోచించి, చర్చించి రాయండి

1. [latex]\sqrt{2}[/latex] ను [latex]\frac{\sqrt{2}}{1}[/latex] గా అంటే [latex]\frac{p}{q}[/latex] రూపంలో రాయవచ్చు కనుక ఇది ఒక అకరణీయ సంఖ్య అని కృతి చెప్పింది. నీవు ఆమె వాదనతో ఏకీభవిస్తావా ? (పేజీ నెం. 10)
సాధన.
నేను ఏకీభవించను, ఎందుకనగా
[latex]\sqrt{2}[/latex] ను [latex]\frac{\sqrt{2}}{1}[/latex] గా వ్రాయడమన్నది [latex]\frac{p}{q}[/latex] రూపము కాదు. [latex]\frac{p}{q}[/latex]లో p మరియు q లు పూర్ణసంఖ్యలు కాని [latex]\sqrt{2}[/latex] పూర్ణసంఖ్య కాదు.

తరగతి కృత్యం

“వర్గమూల సర్పిలం” నిర్మించుట. (పేజీ నెం. 15)
వర్గమూల సర్పిలాన్ని నిర్మించుటకు పెద్ద సైజు కాగితాన్ని తీసుకొని కింద సూచించిన సోపానాలనుసరించండి.
సాధన.

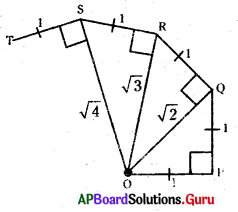
సోపానం 1 : ‘O’ బిందువు నుంచి ప్రారంభించి 1 సెం.మీ. పొడవు గల రేఖాఖండం [latex]\overline{\mathrm{OP}}[/latex] ని గీయండి.
సోపానం 2 : [latex]\overline{\mathrm{OP}}[/latex] కి లంబంగా [latex]\overline{\mathrm{PQ}}[/latex] ను 1 సెం.మీ.
పొడవుగా PO ను గీయండి.
(ఇక్కడ OP = PQ = 14 సెం.మీ.)
సోపానం 3 : O, Q లను కలపండి. (OQ = [latex]\sqrt{2}[/latex])
సోపానం 4 : QR = 1 సెం.మీ. పొడవుతోOQ కు లంబంగా రేఖాఖండాన్ని గీయండి.
సోపానం 5 : O, R లను కలపండి. (OR = [latex]\sqrt{3}[/latex])
సోపానం 6 : RS = 1 సెం.మీ. పొడవుతో [latex]\overline{\mathrm{OR}}[/latex] కు లంబంగా RS రేఖాఖండాన్ని గీయండి.
సోపానం 7 : ఇదే పద్ధతిని మరికొన్ని సోపానాలకు కొనసాగించండి. అప్పుడు [latex]\overline{\mathrm{PQ}}, \overline{\mathrm{QR}}, \overline{\mathrm{RS}}, \overline{\mathrm{ST}}, \overline{\mathrm{TU}}[/latex] ……. రేఖాఖండాలచే ఒక అందమయిన సర్పిలాకారం ఏర్పడుటను చూడవచ్చు. ఇక్కడ [latex]\overline{\mathrm{OQ}}, \overline{\mathrm{OR}}, \overline{\mathrm{OS}}, \overline{\mathrm{OT}}, \overline{\mathrm{OU}}[/latex] లు వరుసగా [latex]\sqrt{2}, \sqrt{3}, \sqrt{4}, \sqrt{5}, \sqrt{6}[/latex] లను సూచిస్తాయి.

ఉదాహరణలు

1. [latex]\frac {5}{3}[/latex] మరియు -[latex]\frac {5}{3}[/latex] లను సంఖ్యారేఖపై సూచించండి. (పేజీ నెం. 3)
సాధన.
– 2, -1, 0, 1, 2 లను సూచిస్తూ ఒక పూర్ణ సంఖ్యారేఖ గీయండి.

సున్నాకు కుడి మరియు ఎడమల వైపు ప్రతి యూనిట్ ను మూడు సమాన భాగాలుగా చేయండి. ఇందు నుంచి 5 భాగాలను తీసుకోండి. సున్నా నుంచి కుడివైపుగల ఐదవ బిందువు [latex]\frac {5}{3}[/latex] ను మరియు ఎడమవైపుగల ఐదవ బిందువు -[latex]\frac {5}{3}[/latex] ను సూచిస్తుంది.

2. కింది వాక్యాలలో సరియైనవి ఏవి ? మీ జవాబును ఒక ఉదాహరణతో సమర్థించండి.
i) ప్రతి అకరణీయ సంఖ్య ఒక పూర్ణ సంఖ్య అవుతుంది.
ii) ప్రతి పూర్ణ సంఖ్య ఒక అకరణీయ సంఖ్య అవుతుంది.
iii) సున్నా ఒక అకరణీయ సంఖ్య. (పేజీ నెం. 3)
సాధన.
i) సరికాదు. ఉదాహరణకు [latex]\frac {7}{8}[/latex] ఒక అకరణీయ సంఖ్య కాని పూర్ణ సంఖ్య కాదు.

ii) సరియైనది. ఎందుకంటే ఏ పూర్ణ సంఖ్యనయినా [latex]\frac{\mathrm{p}}{\mathrm{q}}[/latex] (q ≠ 0) రూపంలో రాయవచ్చు. ఉదాహరణకు -2 ఒక పూర్ణ సంఖ్య – 2 = [latex]\frac{-2}{1}=\frac{-4}{2}[/latex] ఒక అకరణీయ సంఖ్య (ఏదేని పూర్ణసంఖ్య ‘b’ ని [latex]\frac{b}{1}[/latex]గా గాయవచ్చు.)

iii) సరియైనది. ఎందుకంటే 0 ను [latex]\frac{0}{2}, \frac{0}{7}, \frac{0}{13}[/latex]గా రాయవచ్చు. (‘0’ ను [latex]\frac{0}{x}[/latex]గా రాయవచ్చు. ఇక్కడ ‘x’ పూర్ణసంఖ్య మరియు x ≠ 0)

3. 3 మరియు 4 ల మధ్య రెండు అకరణీయ సంఖ్యలను సగటు పద్ధతిలో కనుగొనండి. (పేజీ నెం. 4)
సాధన.
1వ పద్ధతి : a మరియు b ల మధ్య [latex]\frac{a+b}{2}[/latex] అను అకరణీయ సంఖ్య ఉంటుంది. ఇక్కడ a = 3 మరియు b = 4, ([latex]\frac{a+b}{2}[/latex]), ‘a’, ‘b’ల సగటు అని, అది ‘a’, ‘b’ల మధ్య ఉండునని మనకు తెలుసు.
కాబట్టి, ([latex]\frac{(3+4)}{2}=\frac{7}{2}[/latex]) = 1 అను అకరణీయ సంఖ్య 3 మరియు 4 ల మధ్య ఉంటుంది. 3 < [latex]\frac {7}{2}[/latex] < 4
ఈ పద్దతిని కొనసాగిస్తే 3 మరియు 4 ల మధ్య మరికొన్ని అకరణీయ సంఖ్యలనుంచవచ్చు.

2వ పద్ధతి : మరొక సులభమయిన పద్ధతిని గమనిద్దాం. మనం రెండు అకరణీయ సంఖ్యలుంచాలి కాబట్టి 3, 4లను 2 + 1 = 3 హారాలుగా గల అకరణీయ సంఖ్యలుగా రాస్తాము.
అనగా 3 = [latex]\frac{3}{1}=\frac{6}{2}=\frac{9}{3}[/latex] మరియు
4 = [latex]\frac{4}{1}=\frac{8}{2}=\frac{12}{3}=\frac{16}{4}[/latex]
కాబట్టి 3 మరియు 4ల మధ్య [latex]\frac{10}{3}, \frac{11}{3}[/latex] లు రెండు అకరణీయ సంఖ్యలు అవుతాయి.
3 = [latex]\frac{9}{3}<\left(\frac{10}{3}<\frac{11}{3}\right)<\frac{12}{3}[/latex] = 4
ఇప్పుడు మనం 3, 4 ల మధ్య ఐదు అకరణీయ సంఖ్యలుంచాలి అంటే 3, 4 లను 5 + 1 = 6 హారాలుగా గల అకరణీయ సంఖ్యలుగా రాస్తాము.
అనగా 3 = [latex]\frac{18}{6}[/latex] మరియు 4 = [latex]\frac {24}{6}[/latex]

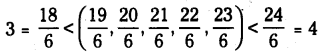
ఈ విధంగా 3, 4ల మధ్య అనంతమయిన అకరణీయ సంఖ్యలుంటాయని మనకు తెలుస్తుంది. మరి ఏవైనా రెండు వేరే అకరణీయ సంఖ్యల మధ్య కూడా ఇదే విధంగా లెక్కలేనన్ని అకరణీయ సంఖ్యలుంటాయని చూపవచ్చా ? ప్రయత్నించండి. దీని నుంచి మనం ఏ రెండు అకరణీయ సంఖ్యల మధ్యనైనా అనంతమైన సంఖ్యలో అకరణీయ సంఖ్యలు వ్యవస్థితమవుతాయని చెప్పవచ్చు.

4. [latex]\frac {7}{16}[/latex], [latex]\frac {2}{3}[/latex] మరియు [latex]\frac {10}{7}[/latex] లను దశాంశ భిన్నాలుగా రాయండి. (పేజీ నెం. 5)
సాధన.

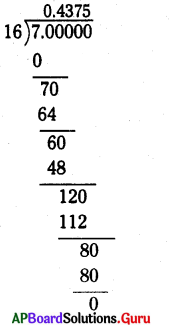
[latex]\frac {7}{16}[/latex] = 0.4375 అంతమయ్యే దశాంశం.

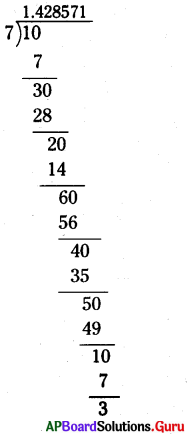
[latex]\frac {10}{7}[/latex] = [latex]1 . \overline{428571}[/latex] అంతంకాని ఆవర్తిత దశాంశం.

[latex]\frac {2}{3}[/latex] = 0.666 = [latex]0 . \overline{6}[/latex] అంతంకాని ఆవర్తిత దశాంశం.

5. 3.28 ని [latex]\frac{\mathrm{p}}{\mathrm{q}}[/latex] రూపంలో రాయండి. (ఇక్కడ q ≠ 0 మరియు p, q లు పూర్ణ సంఖ్యలు) (పేజీ నెం. 5)
సాధన.

6. [latex]1 . \overline{62}[/latex]ను [latex]\frac{\mathrm{p}}{\mathrm{q}}[/latex] రూపంలో రాయండి. p, q లు పూర్ణసంఖ్యలు మరియు q ≠ 0. (పేజీ నెం. 6)
సాధన.
x = 1.626262 ……. (1) అనుకొనుము.
సమీకరణం (1)ని ఇరువైపులా 100 చే గుణించగా
100x = 162.6262 ….. (2)
సమీకరణం (2) నుంచి (1) ని తీసివేయగా

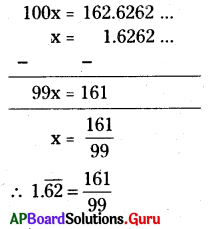
7. [latex]\sqrt{2}[/latex]ను సంఖ్యారేఖపై సూచించండి. (పేజీ నెం. 11)
సాధన.
ఒక యూనిట్ భుజముగాగల చతురస్రం OABC ని సంఖ్యారేఖపై 0 వద్ద గీయండి.
పైథాగరస్ సిద్ధాంతం ప్రకారం
OB = [latex]\sqrt{1^{2}+1^{2}}=\sqrt{2}[/latex]

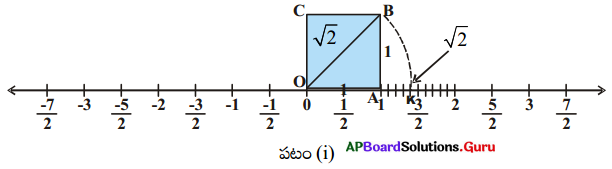
OB = [latex]\sqrt{2}[/latex] అని మనకు తెలుసు. ఒక వృత్తలేఖినిని ఉపయోగించి O కేంద్రంగా OB వ్యాసార్థంతో సంఖ్యారేఖపై O కు కుడివైపున K వద్ద ఖండించునట్లుగా ఒక చాపాన్ని గీయండి.
K అనునది సంఖ్యారేఖ పై [latex]\sqrt{2}[/latex] ను సూచిస్తుంది.

8. [latex]\sqrt{3}[/latex] ను సంఖ్యారేఖపై సూచించండి. (పేజీ నెం. 11)
సాధన.
పటం (i) ను ఒకసారి గుర్తుకు తెచ్చుకోండి.

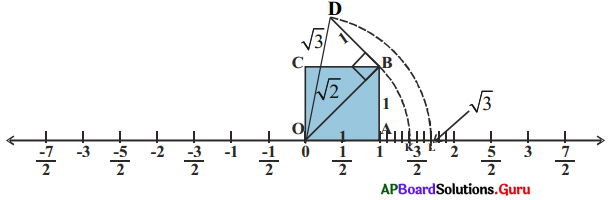
పటం (ii)
పటం (ii) లో 1 యూనిట్ ప్రమాణంలో BD ని OB కి లంబంగా ఉండే విధంగా గీయండి. O, D లను కలపండి.
పైథాగరస్ సిద్ధాంతము ప్రకారం
OD = [latex]\sqrt{(\sqrt{2})^{2}+1^{2}}=\sqrt{2+1}[/latex] = [latex]\sqrt{3}[/latex]
ఒక వృత్తలేఖినిని ఉపయోగించి O కేంద్రంగా OD వ్యాసార్ధంతో సంఖ్యారేఖపై 0 కు కుడివైపున ‘L’ వద్ద ఖండించునట్లు ఒక చాపాన్ని గీయండి. ‘L’ అనునది సంఖ్యారేఖపై [latex]\sqrt{3}[/latex] ను సూచిస్తుంది. ఈ విధంగా ఏదైనా ధనపూర్ణసంఖ్య n కు [latex]\sqrt{n-1}[/latex] ను సంఖ్యారేఖ పై సూచించిన తరువాత [latex]\sqrt{n}[/latex] ను సూచించవచ్చు.

9. [latex]\frac {1}{5}[/latex] మరియు [latex]\frac {2}{7}[/latex] ల మధ్యగల పై రెండు కరణీయ సంఖ్యలు కనుగొనండి. (పేజీ నెం. 13)
సాధన.
[latex]\frac {1}{5}[/latex] = 0.20 అని మనకు తెలుసు.
[latex]\frac {2}{7}[/latex] = [latex]0 . \overline{285714}[/latex]
[latex]\frac {1}{5}[/latex] మరియు [latex]\frac {2}{7}[/latex] ల దశాంశ రూపాలను పరిశీలించండి.
ఈ రెండింటి మధ్య అనంతమయిన కరణీయ సంఖ్యలు ఉంచవచ్చు. ఉదాహరణకు …..
0.201201120111 …………
0.24114111411114 ……..,
0.25231617181912 ……..,
0.267812147512 ……….,
ఇలాగే [latex]\frac {1}{5}[/latex] మరియు [latex]\frac {2}{7}[/latex] ల మధ్య మరో నాలుగు కరణీయ సంఖ్యలు రాయగలవా ?

10. 3 మరియు 4 ల మధ్యగల ఒక కరణీయ సంఖ్యను రాయండి. (పేజీ నెం. 13)
సాధన.
ab ఒక సంపూర్ణ వర్గం కాకుండునట్లు a, b లు ఏవయినా రెండు ధన అకరణీయ సంఖ్యలయితే [latex]\sqrt{a b}[/latex] అనునది a, b ల మధ్య ఉండే కరణీయ సంఖ్య అవుతుంది.
∴ 3 మరియు 4 ల మధ్య కరణీయ సంఖ్య
= [latex]\sqrt{3 \times 4}[/latex] = [latex]\sqrt{3} \times \sqrt{4}[/latex]
= [latex]\sqrt{3} \times 2[/latex] = [latex]2 \sqrt{3}[/latex]

11. కింది లబ్దాలు కరణీయ సంఖ్యలు అవుతాయో లేక అకరణీయ సంఖ్యలవుతాయో తెలపండి. (పేజీ నెం. 13)
i) (3 + [latex]\sqrt{3}[/latex]) + (3 – [latex]\sqrt{3}[/latex])
ii) (3 + [latex]\sqrt{3}[/latex]) (3 – [latex]\sqrt{3}[/latex])
iii) [latex]\frac{10}{2 \sqrt{5}}[/latex]
iv) ([latex]\sqrt{2}[/latex] + 2)²
సాధన.
i) (3+ [latex]\sqrt{3}[/latex]) + (3 – [latex]\sqrt{3}[/latex])
= 3 + [latex]\sqrt{3}[/latex] + 3 – [latex]\sqrt{3}[/latex]
= 6, ఒక అకరణీయ సంఖ్య.

ii) (3 + [latex]\sqrt{3}[/latex]) (3 – [latex]\sqrt{3}[/latex])
(a + b) (a – b) = a² – b²అని మనకు తెలుసు.
(3 + [latex]\sqrt{3}[/latex]) (3 – [latex]\sqrt{3}[/latex]) = 3² – ([latex]\sqrt{3}[/latex])²
= 9 – 3 = 6,
ఒక అకరణీయ సంఖ్య.

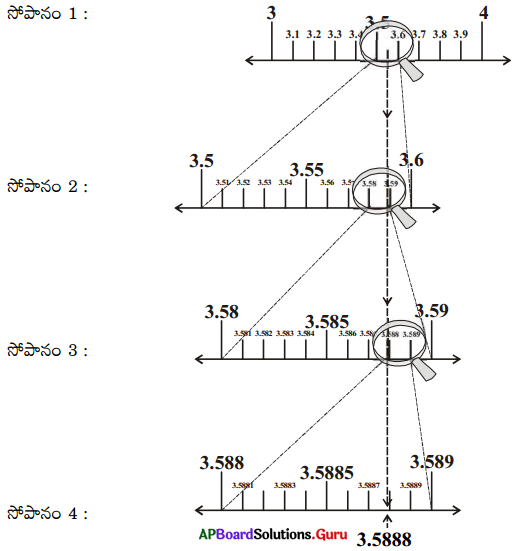
12. [latex]3.5 \overline{8}[/latex] ను 4 దశాంశ స్థానాల వరకు క్రమానుగత వర్ధన పద్ధతిలో సంఖ్యారేఖపై చూపించండి. (పేజీ నెం. 17)
సాధన.
క్రమానుగత వర్ధన పద్ధతిని 3.5888 ని గుర్తించండి.

13. (i) 5[latex]\sqrt{2}[/latex] (ii) [latex]\frac{5}{\sqrt{2}}[/latex] (ii) 21 + [latex]\sqrt{3}[/latex] (iv) π + 3లు కరణీయ సంఖ్యలవుతాయేమో చూడండి. (పేజీ నెం. 18)
సాధన.
[latex]\sqrt{2}[/latex] = 1.414 .., [latex]\sqrt{3}[/latex] = 1.732 …, π = 3.1415 … అని మనకు తెలుసు.
(i) 5[latex]\sqrt{2}[/latex] = 5(1.414 …) = 7.070 ….
(ii) [latex]\frac{5}{\sqrt{2}}[/latex] = [latex]\frac{5}{\sqrt{2}} \times \frac{\sqrt{2}}{\sqrt{2}}=\frac{5 \sqrt{2}}{2}=\frac{7.070}{2}[/latex] = 3.535 … (i నుంచి)
(iii) 21 + [latex]\sqrt{3}[/latex] = 21 + 1.732 = 22.732 ….
(iv) π + 3 = 3.1415 … + 3 = 6.1415 ……..

ఇవన్నీ అంతము మరియు ఆవర్తితం కాని దశాంశాలు. కాబట్టి ఇవి కరణీయ సంఖ్యలు.

14. 5[latex]\sqrt{3}[/latex] + 7[latex]\sqrt{5}[/latex] ను 3[latex]\sqrt{5}[/latex] – 7[latex]\sqrt{3}[/latex] నుండి తీసివేయండి. (పేజీ నెం. 18)
సాధన.
(3[latex]\sqrt{5}[/latex] – 7[latex]\sqrt{3}[/latex]) – (5[latex]\sqrt{3}[/latex] + 7[latex]\sqrt{5}[/latex])
= 3[latex]\sqrt{5}[/latex] – 7[latex]\sqrt{3}[/latex] – 5[latex]\sqrt{3}[/latex] – 7[latex]\sqrt{5}[/latex]
= -4[latex]\sqrt{5}[/latex] – 12[latex]\sqrt{3}[/latex]
= – (4[latex]\sqrt{5}[/latex] + 12[latex]\sqrt{3}[/latex])

15. 6[latex]\sqrt{3}[/latex]ను 13[latex]\sqrt{3}[/latex] తో గుణించండి. (పేజీ నెం. 19)
సాధన:
6[latex]\sqrt{3}[/latex] × 13[latex]\sqrt{3}[/latex] = 6 × 13 × [latex]\sqrt{3}[/latex] × [latex]\sqrt{3}[/latex] = 78 × 3 = 234
వర్గమూలాలకు సంబంధించిన కొన్ని ధర్మాలు కింద ఇవ్వబడినవి.
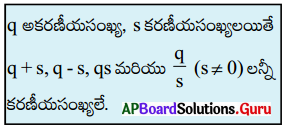
a, b లు ఏవైనా రెండు వాస్తవసంఖ్యలు అయితే

ఈ ధర్మాలనుపయోగించే వివిధ సందర్భాలను ఇప్పుడు మనం చూద్దాం.

16. కింది సమాసాలను సూక్ష్మీకరించండి. (పేజీ నెం. 19)
i) (3 + [latex]\sqrt{3}[/latex]) (2 + [latex]\sqrt{2}[/latex])
ii) (2 + [latex]\sqrt{3}[/latex]) (2 – [latex]\sqrt{3}[/latex])
iii) ([latex]\sqrt{5}[/latex] + [latex]\sqrt{2}[/latex])²
iv) ([latex]\sqrt{5}[/latex] – [latex]\sqrt{2}[/latex]) ([latex]\sqrt{5}[/latex] + [latex]\sqrt{2}[/latex])
సాధన.
i) (3 + [latex]\sqrt{3}[/latex]) (2 + [latex]\sqrt{2}[/latex])
= 6 + 3[latex]\sqrt{2}[/latex] + 2[latex]\sqrt{3}[/latex] + [latex]\sqrt{6}[/latex]
ii) (2 + [latex]\sqrt{3}[/latex]) (2 – [latex]\sqrt{3}[/latex]) = 2² – ([latex]\sqrt{3}[/latex])²
4 – 3 = 1
iii) ([latex]\sqrt{5}[/latex] + [latex]\sqrt{2}[/latex])²
= ([latex]\sqrt{5}[/latex])2 + 2[latex]\sqrt{5}[/latex][latex]\sqrt{2}[/latex] + ([latex]\sqrt{2}[/latex])²
= 5 + 2[latex]\sqrt{10}[/latex] + 2 = 7 + 2[latex]\sqrt{10}[/latex]
iv) ([latex]\sqrt{5}[/latex] – [latex]\sqrt{2}[/latex]) ([latex]\sqrt{5}[/latex] + [latex]\sqrt{2}[/latex])
= ([latex]\sqrt{5}[/latex])² – ([latex]\sqrt{2}[/latex])² = 5 – 2 = 3

17. [latex]\sqrt{5}[/latex] యొక్క హారాన్ని అకరణీయం చేయండి. (పేజీ నెం. 21)
సాధన.
[latex](a+\sqrt{b})(a-\sqrt{b})[/latex] = a² – b అని మనకు తెలుసు.
[latex]\frac{1}{4+\sqrt{5}}[/latex] యొక్క లవహారాలను 4 – [latex]\sqrt{5}[/latex] తో గుణించగా

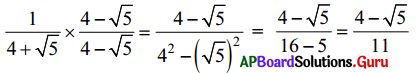
18. [latex]\frac{1}{7+4 \sqrt{3}}[/latex] యొక్క హారాన్ని అకరణీయం చేయండి. (పేజీ నెం. 21)
సాధన.

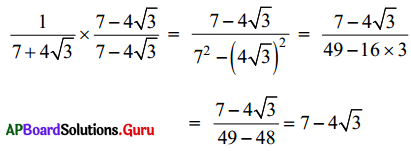
19. [latex]\frac{1}{7+4 \sqrt{3}}+\frac{1}{2+\sqrt{5}}[/latex] ను సూక్ష్మీకరించండి. (పేజీ నెం. 21)
సాధన.
7 + 4[latex]\sqrt{3}[/latex] యొక్క అకరణీయ కారణాంకం 7 – 4[latex]\sqrt{3}[/latex] మరియు 2 + [latex]\sqrt{5}[/latex] యొక్క అకరణీయ కారణాంకం 2 – [latex]\sqrt{5}[/latex]

20. సూక్ష్మీకరించండి. (పేజీ నెం. 23)

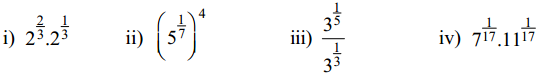
సాధన.