AP State Syllabus AP Board 9th Class Maths Solutions Chapter 1 Real Numbers Ex 1.1 Textbook Questions and Answers.
AP State Syllabus 9th Class Maths Solutions 1st Lesson Real Numbers Exercise 1.1
Question 1.
a) Write any three rational numbers.
Solution:
[latex]\frac{3}{4}, \frac{5}{9}, \frac{2}{7}[/latex]
b) Explain rational number is in your own words.
Solution:
A number which can be expressed in algebraic form i.e., in [latex]\frac { p }{ q }[/latex] form is called a rational number.
E.g.: [latex]\frac { 3 }{ 5 }[/latex], [latex]\frac { -4 }{ 9 }[/latex] etc.
![]()
Question 2.
Give one example each to the following statements.
i) A number which is rational but not an integer.
Solution:
7/11
ii) A whole number which is not a natural number.
Solution:
‘0’ (Zero)
iii) An integer which is not a whole number.
Solution:
-8
iv) A number which is natural number, whole number, integer and rational number.
Solution:
5
v) A number which is an integer but not a natural number.
Solution:
-4
Question 3.
Find five rational numbers between 1 and 2.
Solution:
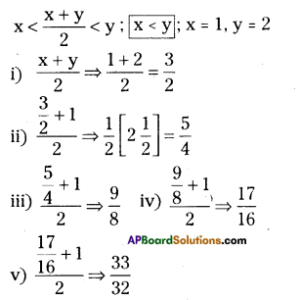
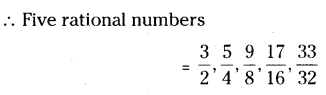
![]()
Question 4.
Five rational numbers between [latex]\frac { 2 }{ 3 }[/latex] and [latex]\frac { 3 }{ 5 }[/latex]
Solution:

Question 5.
Represent [latex]\frac { 8 }{ 5 }[/latex] and [latex]\frac { -8 }{ 5 }[/latex] on a number line.
Solution:

Step – 1 : Draw a number line.
Step – 2 : Divide each unit into 5 equal parts.
Step – 3 : Take 8 – equal parts from ‘0’ on its right side and mark it as [latex]\frac { 8 }{ 5 }[/latex] (similarly) on left side [latex]\frac { -8 }{ 5 }[/latex] .
Question 6.
Express the following rational numbers as decimal numbers.
Solution:
I. i) [latex]\frac { 242 }{ 1000 }[/latex] .
ii) [latex]\frac { 354 }{ 500 }[/latex] .
iii) [latex]\frac { 2 }{ 5 }[/latex] .
iv) [latex]\frac{115}{4}[/latex]
Solution:
i) [latex]\frac { 242 }{ 1000 }[/latex] = 0.242
ii) [latex]\frac{354}{500}[/latex]
[latex]=\frac{354 \times 2}{500 \times 2}[/latex]
[latex]=\frac{708}{1000}[/latex]
[latex]=0.708[/latex]
iii) [latex]\frac{2}{5}[/latex]
[latex]=\frac{2 \times 2}{5 \times 2}[/latex]
[latex]=\frac{4}{10}[/latex]
[latex]=0.4[/latex]
iv)

![]()
II. i) [latex]\frac{2}{3}[/latex]
Solution:

ii) [latex]\frac{-25}{36}[/latex]
Solution:

iii) [latex]\frac{22}{7}[/latex]
Solution:

iv) [latex]\frac{11}{9}[/latex]
Solution:
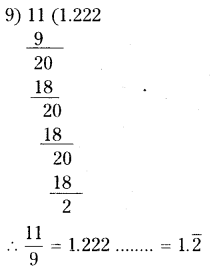
![]()
Question 7.
Express each of the following decimals in [latex]\frac{p}{q}[/latex] form where q ≠ 0 and p, q are integers.
i) 0.36
Solution:
0.36 = [latex]\frac{36}{100}=\frac{9}{25}[/latex]
ii) 15.4
Solution:
15.4 = [latex]\frac{154}{10}=\frac{77}{5}[/latex]
iii) 10.25
Solution:
10.25 = [latex]\frac{1025}{100}=\frac{41}{4}[/latex]
iv) 3.25
Solution:
3.25 = [latex]\frac{325}{100}=\frac{13}{4}[/latex]
Question 8.
Express each of the following decimal number in the [latex]\frac { p }{ q }[/latex] form.
i) [latex]0 . \overline{5}[/latex]
Solution:
Let x = [latex]0 . \overline{5}[/latex] = 0.5555
Multiplying both sides by 10

ii) [latex]3 . \overline{8}[/latex]
Solution:
Let x = [latex]3 . \overline{8}[/latex]
(i.e) x = 3.888 ………..
Multiplying both sides by 10
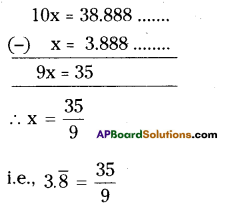
![]()
iii) [latex]0 . \overline{36}[/latex]
Solution:
Let x [latex]0 . \overline{36}[/latex]
(i.e) x = 0.363636 ………..
Multiplying by 100 on both sides
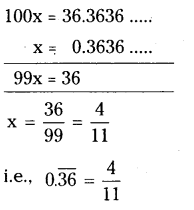
iv) [latex]3.12 \overline{7}[/latex]
Solution:
Let x = [latex]3.12 \overline{7}[/latex]
x = 0.12777
Multiplying by 10 on both sides

Question 9.
Without actually dividing find which of the following are terminating
decimals.
i) [latex]\frac { 3 }{ 25 }[/latex]
Solution:
Check the denominator, if it consists of 2’s or 5’s or combination of both then only it reduces to a terminating decimal.
25 = 5 x 5
Hence [latex]\frac { 3 }{ 25 }[/latex] is a terminating decimal.
ii) [latex]\frac { 11 }{ 18 }[/latex]
Solution:
Denominator 18 = 2 × 3 × 3,
hence [latex]\frac { 11 }{ 18 }[/latex] is a non-terminating decimal 13
iii) [latex]\frac { 13 }{ 20 }[/latex]
Denominator 20 = 2 × 2 × 5,
hence [latex]\frac { 13 }{ 20 }[/latex] is a terminating decimal.
iv) [latex]\frac { 41 }{ 42 }[/latex]
Solution:
Denominator 42 = 2 × 3 × 7,
hence [latex]\frac { 41 }{ 42 }[/latex] is a non-terminating decimal.
![]()