AP Board 8th Class Maths Solutions Chapter 9 సమతల పటముల వైశాల్యములు InText Questions

AP SCERT 8th Class Maths Textbook Solutions Chapter 9 సమతల పటముల వైశాల్యములు InText Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 9th Lesson సమతల పటముల వైశాల్యములు InText Questions

ఇవి చేయండి

1. ఈ క్రింది పటముల యొక్క వైశాల్యములను కనుక్కోండి. (పేజీ నెం. 200)

ప్రశ్న (i)

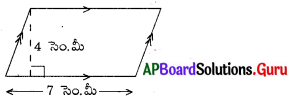
సాధన.
సమాంతర చతుర్భుజం భూమి, b = 7 సెం.మీ
సమాంతర భుజాల మధ్య దూరం, h = 4 సెం.మీ
సమాంతర చతుర్భుజ వైశాల్యం, A = b × h
=7 × 4
= 28 చ.సెం.మీ

ప్రశ్న (ii)

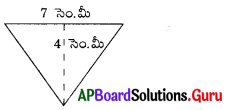
సాధన.
త్రిభుజ భూమి, b = 7 సెం.మీ
త్రిభుజ ఎత్తు, h = 4 సెం.మీ
త్రిభుజ వైశాల్యం, A = \(\frac {1}{2}\) × b × h
= \(\frac {1}{2}\) × 7 × 4
= 14 చ.సెం.మీ

ప్రశ్న (iii)

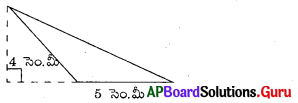
సాధన.
త్రిభుజ భూమి, b = 5 సెం.మీ
త్రిభుజ ఎత్తు, h = 4 సెం.మీ
త్రిభుజ వైశాల్యం, A = \(\frac {1}{2}\) × b × h
= \(\frac {1}{2}\) × 5 × 4
= 10 చ.సెం.మీ

ప్రశ్న (iv)

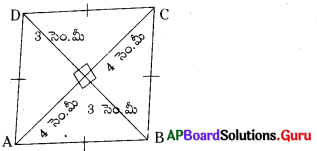
సాధన.
రాంబస్ యొక్క మొదటి కర్ణం,
AC = d₁ = 4 + 4 – 8 సెం.మీ
రాంబస్ యొక్క రెండవ కర్ణం,
BD = d₂ = 3 + 3 = 6 సెం.మీ
రాంబస్ వైశాల్యం, A = \(\frac {1}{2}\)d₁ d₂
= \(\frac {1}{2}\) × 8 × 6
= 24 చ.సెం.మీ

ప్రశ్న (v)

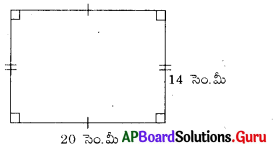
సాధన.
దీర్ఘ చతురస్ర పొడవు, l = 20 సెం.మీ
దీర్ఘ చతురస్ర వెడల్పు, b = 14 సెం.మీ
దీర్ఘ చతురస్ర వైశాల్యం, A = l × b
= 20 × 14
= 280 చ.సెం.మీ

ప్రశ్న (vi)

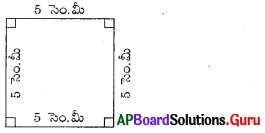
సాధన.
చతురస్ర భుజం, s = 5 సెం.మీ
చతురస్ర వైశాల్యం , A = s × s
= 5 × 5
= 25 చ.సెం.మీ

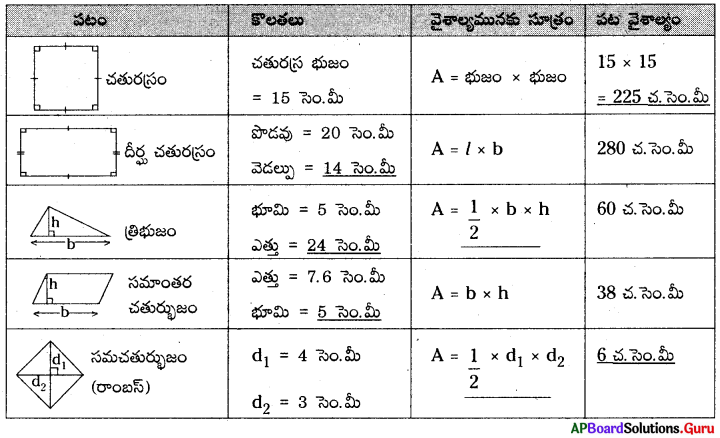
2. కొన్ని సమతల పటముల యొక్క కొలతలు ఈ క్రింది పట్టికలో ఇవ్వబడినవి. ఇచ్చిన సమాచారం అసంపూర్తిగా యున్నది. లోపించిన సమాచారమును కనుగొనుము. (పేజీ నెం. 200)
సాధన.

3. ఈ క్రింది సమలంబ చతుర్భుజము యొక్క వైశాల్యములను కనుక్కోండి. (పేజీ నెం. 204)
పటము (i)

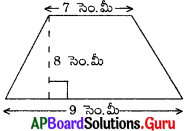
సాధన.
సమాంతర భుజాల పొడవులు, a = 9 సెం.మీ
b = 7 సెం.మీ
సమాంతర భుజాల మధ్య దూరం, h = 8 సెం.మీ
సమలంబ చతుర్భుజ వైశాల్యం,
A = \(\frac {1}{2}\) h(a + b) = \(\frac {1}{2}\) × 8 (9 + 7)
= 4(16) = 64 చ.సెం.మీ

పటము (ii)

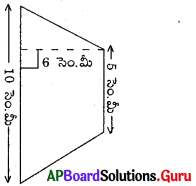
సాధన.
సమాంతర భుజాల పొడవులు, a = 10 సెం.మీ
b = 5 సెం.మీ
సమాంతర భుజాల మధ్య దూరం, h = 6 సెం.మీ
సమలంబ చతుర్భుజ వైశాల్యం,
A = \(\frac {1}{2}\)h(a + b)
= \(\frac {1}{2}\) × 6(10 + 5)
= 3(15) = 45 చ.సెం.మీ

4. సమలంబ చతుర్భుజ వైశాల్యం 16 చ.సెం.మీ. సమాంతర భుజాలలో ఒక భుజం పొడవు 5 సెం.మీ. మరియు వాటి మధ్యదూరం 4 సెం.మీ. రెండవ సమాంతర భుజం యొక్క పొడవును కనుగొనుము. ఈ సమలంబ చతుర్భుజమును గ్రాఫు కాగితముపై గీసి దాని వైశాల్యంతో సరిచూడండి. (పేజీ నెం. 204)
సాధన.

సమలంబ చతుర్భుజ వైశాల్యం , A = 16 చ.సెం.మీ సమాంతర భుజాలలో ఒక భుజం పొడవు a = 5 సెం.మీ సమాంతర భుజాల మధ్య దూరం, 5 = 4 సెం.మీ రెండవ సమాంతర భుజం పొడవు, b = x సెం.మీ అనుకొనుము
సమలంబ చతుర్భుజ వైశాల్యం,

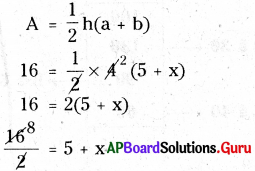
8 = 5 + x
8 – 5 = x
3 = x
x = 3 సెం.మీ
∴ రెండవ సమాంతర భుజం పొడవు,
b = x = 3 సెం.మీ

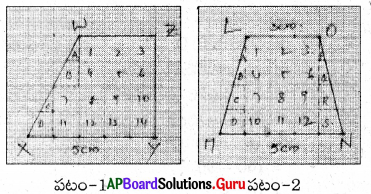
పటం-1 నుండి

14 చతురస్రాల వైశాల్యం = 1 × 14 = 14 చ. సెం.మీ.
D + A = 1 చ. సెం.మీ. ; B + C = 1 చ.సెం.మీ.
∴ WXYZ సమలంబ చతుర్భుజ వైశాల్యం
= 14 + (D+ A) + (B + C)
= 14 + 1 + 1 = 16 చ.సెం.మీ.
(లేదా)
పటం-2 నుండి
12 చతురస్రాల వైశాల్యం = 1 × 12 = 12 చ.సెం.మీ.
D + A = 1 చ.సెం.మీ.; B + C = 1 చ.సెం.మీ.
S + P = 1 చ.సెం.మీ. ; Q + R = 1 చ.సెం.మీ.
∴ LMNO సమలంబ చతుర్భుజ వైశాల్యం
= 12 + 1 + 1 + 1 + 1 = 16 చ.సెం.మీ.

5. ABCD ఒక సమాంతర చతుర్భుజం. దాని వైశాల్యం 100 చ.సెం.మీ. P అనేది పటంలో చూపినట్లు దాని అంతరంలో బిందువు అయిన ∆ APB + ∆ CPDల వైశాల్యం కనుగొనండి. (పేజీ నెం. 204)

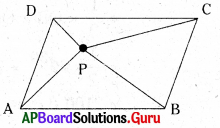
సాధన.
▢^gm ABCD వైశాల్యం = 100 చ.సెం.మీ.
ABCD ఒక సమాంతర చతుర్భుజం, P అనేది దాని అంతరంలో ఏదైనా ఒక బిందువు అయిన
ar (∆APB) + ar (∆CPD) = ar (∆APD) + ar (∆BPC)
∴ ar (∆APB) + ar (∆CPD) = \(\frac {1}{2}\)ar (▢^gm ABCD)
= \(\frac {1}{2}\) × 100
= 50 చ.సెం.మీ

6. ఒక సర్వేయరు ఫీల్డుబుక్ లో నమోదు చేయబడిన ఈ దిగువ వివరాల సహాయంతో పొలం వైశాల్యం కనుగొనండి. (పేజీ నెం. 213)

ప్రశ్న (i)

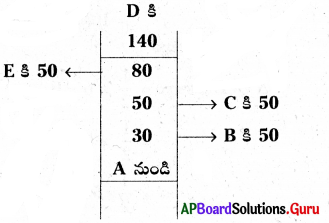
సాధన.

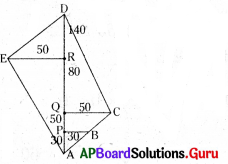
పై పటం నుంచి
(i) పొలం A, B, C, D, E శీర్షాలుగా గల పంచభుజి.
(ii) AD కర్ణంగా తీసుకోబడినది.
(iii) పొలం నాలుగు త్రిభుజాలుగా, ఒక సమలంబ చతుర్భుజంగా విభజింపబడినది.
PQ = AQ – AP
= 50 – 30 = 20
QD = AD – AQ
= 140 – 50 = 90
RD = AD – AR
= 140 – 80 = 60
∆ APB వైశాల్యం :
∆ APB వైశాల్యం = \(\frac {1}{2}\) × b × h
= \(\frac {1}{2}\) × PB × AP

∆ QCD వైశాల్యం :
∆ QCD వైశాల్యం = \(\frac {1}{2}\) × b × h
= \(\frac {1}{2}\) × QC × QD

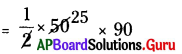
= 2250 చ.యూ

∆ DER వైశాల్యం :
∆ DER వైశాల్యం = \(\frac {1}{2}\) × b × h

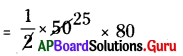
= 25 × 60 = 1500 చ.యూ

∆ ERA వైశాల్యం :
∆ ERA వైశాల్యం = \(\frac {1}{2}\) × b × h
= \(\frac {1}{2}\) × ER × AR
= 25 × 80 = 2000 చ.యూ

∴ పొలం వైశాల్యం

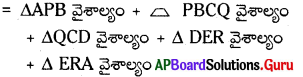
= 450 + 800 + 2250 + 15000 + 2000
= 7000 చ.యూ

ప్రశ్న (ii)

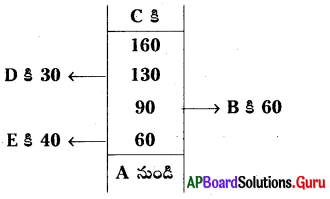
సాధన.

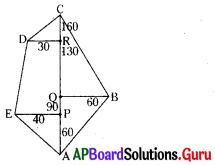
పై పటం నుంచి
(i) పొలం A, B, C, D, E శీర్షాలుగా గల పంచభుజి.
(ii) AC కర్ణంగా తీసుకోబడినది.
(iii) పొలం నాలుగు త్రిభుజాలుగా, ఒక సమలంబ చతుర్భుజంగా విభజింపబడినది.
QC = AC – AQ
= 160 – 90
= 70
RC = AC – AR
= 160 – 130
= 30
PR = AR – AP
= 130 – 60
= 70

∆ AQB వైశాల్యం :
∆ AQB వైశాల్యం = \(\frac {1}{2}\) × b × h
= \(\frac {1}{2}\) × QB × AQ

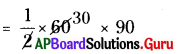
= 2700 చ.యూ

∆ QBC వైశాల్యం :
∆ QBC వైజాల్యం = \(\frac {1}{2}\) × b × h
= \(\frac {1}{2}\) × QB × QC

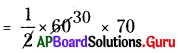
= 2100 చ.యూ

∆ DRC వైశాల్యం :
∆ DRC వైశాల్యం = \(\frac {1}{2}\) × b × h
= \(\frac {1}{2}\) × DR × RC

∆ EPA వైశాల్యం :
∆ EPA వైశాల్యం = \(\frac {1}{2}\) × b × h

= 1200 చ.యూ
∴ పొలం వైశాల్యం

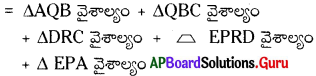
= 2700 + 2100 + 450 + 2450 + 1200
= 8900 చ.యూ

ప్రయత్నించండి

1. ఈ క్రింది చతుర్భుజముల యొక్క వైశాల్యములను కనుగొనండి. (పేజీ నెం. 213)

ప్రశ్న (i)

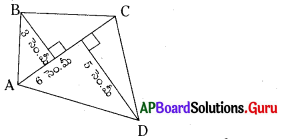
సాధన.
చతుర్భుజ కర్ణం పొడవు, 4 = 6 సెం.మీ
కర్ణం పైకి గీయబడిన లంబాల పొడవులు,
h₁ = 3 సెం.మీ, h₂ = 5 సెం.మీ
చతుర్భుజ వైశాల్యం,

= 3(8) = 24 చ.సెం.మీ

ప్రశ్న (ii)

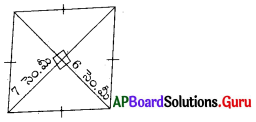
సాధన.
సమచతుర్భుజం యొక్క కర్ణాల పొడవులు,
d₁ = 7 సెం.మీ, d₂ = 6 సెం.మీ
∴ సమచతుర్భుజ (రాంబస్) వైశాల్యం

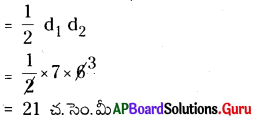
ప్రశ్న (iii)

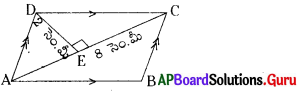
సాధన.
∆ ACD వైశాల్యం :
త్రిభుజ భూమి, b = 8 సెం.మీ
త్రిభుజ ఎత్తు, h = 2 సెం.మీ
∴ ∆ ACD వైశాల్యం = \(\frac {1}{2}\) × b × h
= \(\frac {1}{2}\) × AC × DE
= \(\frac {1}{2}\) × 8 × 2
= 8 చ.సెం.మీ
సమాంతర చతుర్భుజంను దాని కర్ణం రెండు సమాన వైశాల్యాలు గల త్రిభుజాలుగా విభజిస్తుంది.
∴ ∆ ABC వైశాల్యం = ∆ ACD వైశాల్యం
∴ ∆ ABC వైశాల్యం = 8 చ. సెం.మీ
∴ ☐^gm ABCD వైశాల్యం
= ∆ ABC వైశాల్యం + ∆ ACD వైశాల్యం
= 8 + 8
= 16 చ.సెం.మీ

2.

ప్రశ్న (i)
ఈ క్రింద గీయబడిన బహుభుజిని భాగములుగా (త్రిభుజములు మరియు సమలంబ చతుర్భుజం)గా విభజించి వాటి యొక్క వైశాల్యములను కనుగొనండి. (పేజీ నెం. 214)

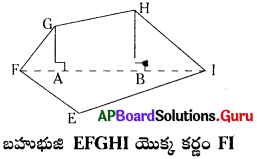
సాధన.
కర్ణం FI పై రెండు లంబములు GA, HBలను గీయుట ద్వారా పంచభుజి EFGHI ను నాలుగు భాగాలుగా విభజించవచ్చును.
పంచభుజి EFGHI వైశాల్యం

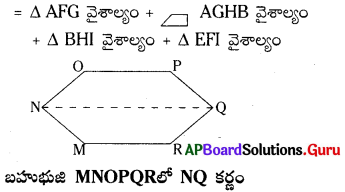
కర్ణం NQ గీయుట ద్వారా షడ్భుజి MNOPQR ను రెండు భాగాలుగా విభజించవచ్చును. షడ్భుజి MNOPOR వైశాల్యం

ప్రశ్న (ii)
ఈ క్రింద గీయబడిన బహుభుజి ABCDE భాగములుగా విభజింపబడింది. (పేజీ నెం. 215)

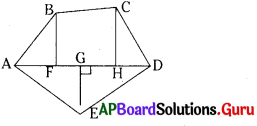
AD = 8 సెం.మీ, AH = 6 సెం.మీ, AF=3 సెం.మీ మరియు లంబము BF= 2 సెం.మీ, CH = 3 సెం.మీ, EG = 2.5 సెం.మీ అయిన వైశాల్యం కనుక్కోండి.
సాధన.
ABCDE బహుభుజి వైశాల్యం = ∆ AFB వైశాల్యం + సమలంబ చతుర్భుజం FBCH వైశాల్యం + ∆ HCD వైశాల్యం + ∆ AED వైశాల్యం
∆ AFB వైశాల్యం = \(\frac {1}{2}\) × AF × BF

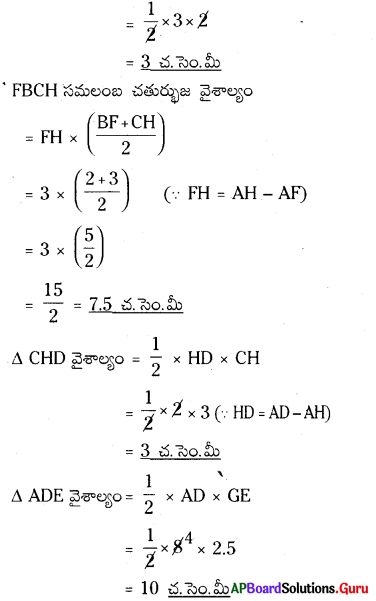
కావున బహుభుజి ABCDE వైశాల్యం = ∆ AFB వైశాల్యం + సమలంబ చతుర్భుజం FBCH వైశాల్యం + ∆ CHD వైశాల్యం + ∆ ADE వైశాల్యం
= 3 + 7.5 + 3 + 10
= 23.5 చ.సెం.మీ

ప్రశ్న (iii)
MNOPQR బహుభుజిలో MP = 9 సెం.మీ, MD = 7 సెం.మీ, MC = 6 సెం.మీ, MB = 4 సెం.మీ, MA = 2 సెం.మీ, అయితే వైశాల్యంను కనుక్కోండి. (పేజీ నెం. 215)

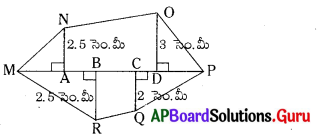
కర్ణం MP పై గీయబడిన లంబాలు NA, OD, QC మరియు RB.
సాధన.

సమలంబ చతుర్భుజం RBCQ వైశాల్యం
= \(\frac {1}{2}\) × BC × (RB + CQ)

∴ బహుభుజి MNOPQR వైశాల్యం = ∆ MAN వైశాల్యం + సమలంబ చతుర్భుజం ANOD వైశాల్యం + ∆DPO వైశాల్యం + ∆CPQ వైశాల్యం + సమలంబ చతుర్భుజం RBCQ వైశాల్యం + ∆RBM వైశాల్యం
= 2.5 + 13.75 + 3 + 3 + 4.5 + 5
= 31.75 చ.సెం.మీ.

ఆలోచించి, చర్చింది వ్రాయండి

1. సమాంతర చతుర్భుజంలో, ఒక కర్ణం గీయడం ద్వారా ఆ సమాంతర చతుర్భుజంను రెండు సర్వసమాన త్రిభుజాలుగా విభజించవచ్చు. ఈ విధముగానే సమలంబ చతుర్భుజమును రెండు సర్వసమాన త్రిభుజాలుగా విభజించగలమా ? (పేజీ నెం. 213)
సాధన.

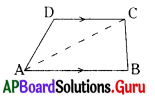
విభజించలేము.
∵ ప్రక్క పటం నుండి ∆ABC ≠ ∆ADC