AP Board 8th Class Maths Solutions Chapter 9 సమతల పటముల వైశాల్యములు Ex 9.2

SCERT AP 8th Class Maths Solutions Chapter 9 సమతల పటముల వైశాల్యములు Ex 9.2 Textbook Exercise Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 9th Lesson సమతల పటముల వైశాల్యములు Exercise 9.2

ప్రశ్న1.
ఒక దీర్ఘచతురస్రాకార షీట్ యొక్క కొలతలు 36 సెం.మీ × 25 సెం.మీ. షీట్ నుండి 3.5 సెం.మీ వ్యాసము కలిగిన 56 వృత్తాకార గుండీలను కత్తిరించగా మిగిలిన షీట్ వైశాల్యము ఎంత ?
సాధన.
దీర్ఘచతురస్రాకార షీట్ కొలతలు = 36 సెం.మీ × 25 సెం.మీ
దీర్ఘచతురస్రాకార షీట్ పొడవు, l = 36 సెం.మీ
దీర్ఘచతురస్రాకార షీట్ వెడల్పు, b = 25 సెం.మీ
∴ దీర్ఘచతురస్రాకార షీట్ వైశాల్యం A = l × b
= 36 × 25 = 900 చ.సెం.మీ
వృత్తాకార గుండీ వ్యాసం, d = 3.5 సెం.మీ
వృత్తాకార గుండీ వ్యాసార్ధం,
r = \(\frac{\mathrm{d}}{2}=\frac{3.5}{2}\) = 1.75 సెం.మీ
ఒక్కొక్క వృత్తాకార గుండీ వైశాల్యం = πr²
= 4 × (1.75)²

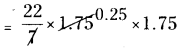
= 22 × 0.25 × 1.75 = 9.6250 చ.సెం.మీ
దీర్ఘచతురస్రాకార షీట్ నుంచి 56 వృత్తాకార గుండీలను కత్తిరించారు.
∴ 56 వృత్తాకార గుండీల వైశాల్యం
= 56 × ఒక్కొక్క వృత్తాకార గుండీ వైశాల్యం
= 56 × 9.6250 = 539 చ.సెం.మీ
మిగిలిన షీట్ వైశాల్యం = దీర్ఘచతురస్రాకార షీట్ వైశాల్యం – 56 వృత్తాకార గుండీల వైశాల్యం
= 900 – 539 = 361 చ.సెం.మీ

ప్రశ్న2.
28 సెం.మీ భుజంగా గల చతురస్రంలో అంతర్లిఖించ బడిన వృత్త వైశాల్యమును కనుగొనుము.

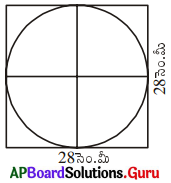
(సూచన : వృత్తము యొక్క వ్యాసము చతురస్ర భుజమునకు సమానము)
సాధన.
వృత్త వ్యాసం, d = చతురస్ర భుజం = 28 సెం.మీ.
వృత్త వ్యా సం, d = 28 సెం.మీ
వృత్త వ్యాసార్ధం, r = \(\frac{\mathrm{d}}{2}\)

ప్రశ్న3.
క్రింది యివ్వబడిన పటములలో షేర్ చేయబడిన ప్రాంత వైశాల్యములను కనుగొనుము.
(i)

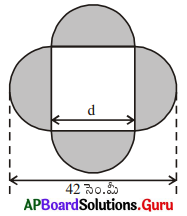
(గమనిక : d + \(\frac{\mathrm{d}}{2}+\frac{\mathrm{d}}{2}\) = 42)
d = 21
∴ చతురస్ర భుజం = 21 సెం.మీ. 42 సెం.మీ
సాధన.
పై పటంలో షేర్ చేయబడిన నాలుగు అర్ధవృత్తాలు
ఒకే చతురస్ర భుజంను వ్యాసాలుగా కలిగియున్నాయి.
∴ నాలుగు అర్ధవృత్తాలు ఒకే వ్యాసాలను కలిగి యుంటాయి.
పై పటం ప్రకారం,

∴ చతురస్ర భుజం, d = 21 సెం.మీ.
అర్ధవృత్త వ్యాసం = చతురస్ర భుజం = 21 సెం.మీ.
అర్ధవృత్త వ్యాసం = 21 సెం.మీ.

షేడ్ చేయబడిన నాలుగు అర్ధవృత్తాల వైశాల్యం
= 4 × ఒక్కొక్క అర్ధవృత్త వైశాల్యం
= 4 × 173.25
= 693 చ.సెం.మీ.

(ii)

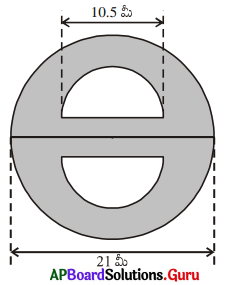
సాధన.
పెద్ద వృత్త వ్యా సం = 21 మీ.

అర్ధవృత్త వ్యాసం = 10.5 మీ.
అర్ధవృత్త వ్యాసార్ధం = \(\frac {10.5}{2}\)
= 5.25 మీ.

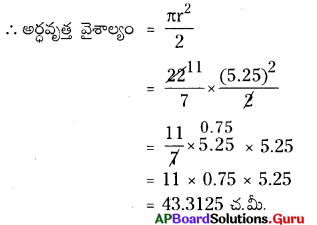
∴ రెండు అర్ధవృత్తాల వైశాల్యం = 2 × 43.3125
= 86.6250 చ.మీ.
∴ షేడ్ చేయబడిన ప్రాంత వైశాల్యం = పెద్ద వృత్త వైశాల్యం – రెండు అర్ధవృత్తాల వైశాల్యం
= 346.5 – 86.6250
= 259.8750 చ.మీ.

ప్రశ్న4.
సమాన వ్యాసార్ధములు కలిగిన 4 అర్ధవృత్తములు మరియు సమాన వ్యాసార్ధాలు కలిగిన రెండు పెద్ద అర్ధవృత్తములు (ప్రతిది 42 సెం.మీ). పటములో చూపిన విధముగా జతచేయబడినవి. అయిన షేడ్ చేయబడిన ప్రాంతము వైశాల్యం కనుగొనండి.

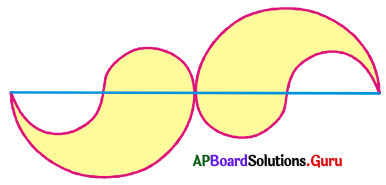
సాధన.
పెద్ద అర్ధవృత్త వ్యాసం, d = 42 సెం.మీ.
పెద్ద అర్ధవృత్త వ్యాసార్థం, r = \(\frac {42}{2}\)
= 21 సెం.మీ.

షేడ్ చేయబడిన ప్రాంత వైశాల్యం = రెండు పెద్ద అర్ధవృత్తాల వైశాల్యం – 2 చిన్న అర్ధవృత్తాల వైశాల్యం + 2 చిన్న అర్ధవృత్తాల వైశాల్యం
= రెండు పెద్ద అర్ధవృత్తాల వైశాల్యం = 2 × పెద్ద అర్ధవృత్త వైశాల్యం
= 2 × 693 = 1386 చ.సెం.మీ.

ప్రశ్న5.
నాలుగు అర్ధవృత్తములు, రెండు పావు వృత్తములు పటంలో చూపిన విధంగా జత చేయబడినవి. OA = OB = OC = OD = 14 సెం.మీ. అయిన షేడ్ చేయబడిన ప్రాంత వైశాల్యమును కనుగొనుము.

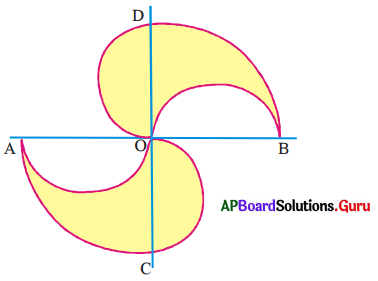
సాధన.

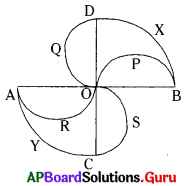
OA = OB = OC = OD = 14 సెం.మీ.
పావు వృత్తం BXD వ్యాసార్ధం, r = 14 సెం.మీ.

∴ పావు వృత్తం AYC వైశాల్యం = 154 చ.సెం.మీ.
∴ షేడ్ చేయబడిన ప్రాంత వైశాల్యం = పావువృత్తం BXD వైశాల్యం – అర్ధవృత్తం OPB వైశాల్యం + అర్ధవృత్తం OQD వైశాల్యం + పావువృత్తం AYC వైశాల్యం – అర్ధవృత్తం ARO వైశాల్యం + అర్ధవృత్తం OSC వైశాల్యం
= పావు వృత్తం BXD వైశాల్యం + పావువృత్తం AYC వైశాల్యం
= 154 + 154 = 308 చ.సెం.మీ.

ప్రశ్న6.
పటంలో చూపిన విధంగా A, B, C మరియు D కేంద్రంగా గల సమాన వ్యాసార్ధములు కలిగిన నాలుగు వృత్తాలు బాహ్యంగా స్పృశించుకొంటున్నాయి. ABCD చతురస్రం యొక్క భుజం 7 సెం.మీ. అయిన షేడ్ చేయబడిన ప్రాంత వైశాల్యం కనుగొనుము.

సాధన.

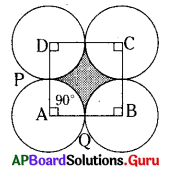
చతురస్ర భుజం, AB = BC = CD = DA = 7 సెం.మీ.
చతురస్ర వైశాల్యం = భుజం × భుజం
= 7 × 7
= 49 సెం.మీ.
పై పటం నుంచి,

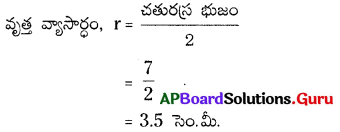
చతురస్రంలో నాలుగు సెక్టార్లు గలవు. నాల్గింటి వైశాల్యాలు సమానం.
APQ సెక్టారు కోణం, x = 90°
వ్యాసార్ధం, r = 3.5 సెం.మీ.
సెక్టారు APQ వైశాల్యం

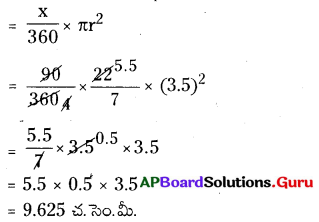
∴ నాలుగు సెక్టార్ల వైశాల్యం = 4 × ఒక్కొక్క సెక్టారు వైశాల్యం
= 4 × 9.625
= 38.5 చ.సెం.మీ.
∴ షేడ్ చేయబడిన ప్రాంత వైశాల్యం = చతురస్రం ABCD వైశాల్యం – 4 సెక్టార్ల వైశాల్యం
= 49 – 38.5 = 10.5 చ.సెం.మీ.

ప్రశ్న7.
ఒక సమబాహు త్రిభుజ వైశాల్యము \(49 \sqrt{3}\) చ.సెం.మీ. వృత్త కేంద్రమును శీర్షములుగా మూడు వృత్తములు బాహ్యముగా పటములో చూపిన విధముగా స్పృశించు కొంటున్నాయి. అయినచో వృత్తమును కలిగియుండని త్రిభుజ ప్రాంత వైశాల్యమును కనుగొనుము.

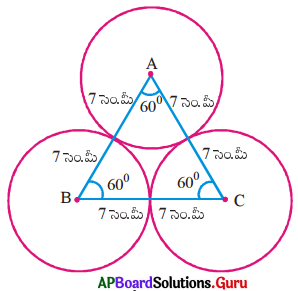
సాధన.
ΔABC ఒక సమబాహు త్రిభుజం,
సమబాహు త్రిభుజం ABC వైశాల్యం = \(49 \sqrt{3}\) చ.సెం.మీ
సమాన వ్యాసార్ధాలు గల మూడు వృత్తాలు బాహ్యంగా స్పృశించుకుంటున్నాయి. ప్రతి వృత్తంలో ఒక సెక్టారు కలదు. మొత్తం మూడు సెక్టారులు గలవు. ప్రతి సెక్టారు కోణం 90° మరియు వ్యాసార్ధం 7 సెం.మీ. కావున మూడు సెక్టారుల వైశాల్యాలు సమానం.
సెక్టారు APQ కోణం, x = 60°
సెక్టారు APQ వ్యాసార్ధం, r = 7 సెం.మీ
∴ సెక్టార్ APQ వైశాల్యం

మూడు సెక్టార్ల వైశాల్యం = 3 × ఒక్కొక్క సెక్టార్ వైశాల్యం

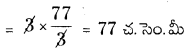
వృత్తమును కలిగియుండని త్రిభుజ ప్రాంత వైశాల్యం = త్రిభుజం ABC వైశాల్యం – మూడు సెక్టార్ల వైశాల్యం
= \(49 \sqrt{3}\) – 77
= 49 × 1.7321 – 77 (∵ \(\sqrt{3}\) = 1.7321)
= 84.8729 – 77
= 7.8729 చ.సెం.మీ

ప్రశ్న8.
(i) ‘a’ వ్యాసార్ధము కలిగిన నాలుగు సమాన వృత్తములు స్పృశించుకొంటున్నాయి. అయినచో ఆ వృత్తముల మధ్య ప్రాంత వైశాల్యం కనుగొనండి.
సాధన.

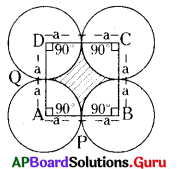
చతురస్రం ABCD భుజం, AB = BC = CD = DA
= a + a = 2a యూ
చతురస్ర వైశాల్యం = భుజం × భుజం
= 2a × 2a = 4a² చ.యూ.
నాలుగు వృత్తాలలో సమాన వైశాల్యాలు గల నాలుగు సెక్టార్లు గలవు.
సెక్టార్ APQ కోణం, x = 90°
సెక్టార్ APQ వ్యాసార్ధం, r = a

నాలుగు సెక్టార్ల వైశాల్యం = 4 × ఒక్కొక్క సెక్టార్ వైశాల్యం

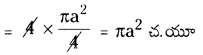
∴ వృత్తముల మధ్య ప్రాంత వైశాల్యం = చతురస్రం ABCD వైశాల్యం – 4 సెక్టార్ల వైశాల్యం
= 4a² – πa² = (4 – π)a² చ.యూ

(ii) నాలుగు వృత్త వ్యాసార్ధములు సమానము మరియు ప్రతి వృత్తము మరో రెండు వృత్తములను బాహ్యంగా స్పృశించుకొంటూ ఉంటే వృత్త కేంద్రములు శీర్షములుగా ఒక చతురస్రమును ఏర్పాటు చేస్తే, ఆ చతురస్ర భుజము 24 మీ॥ అయిన ఆ వృత్తముల మధ్య ప్రాంతమును షేడ్ చేస్తే, షేడ్ చేయవలసిన ప్రాంత వైశాల్యము ఎంత ?
సాధన.

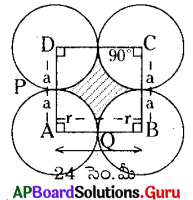
సమాన వ్యాసార్ధం గల నాలుగు వృత్తాలు బాహ్యంగా స్పృశించుకుంటున్నాయి.
చతురస్ర భుజం = 24 సెం.మీ.
పై పటం నుంచి,
r + r = 24
2r = 24

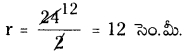
షేడ్ చేయని ప్రాంతము = సమాన వైశాల్యం గల నాలుగు సెక్టార్లు
సెక్టార్ APQ కోణం, x = 90°
సెక్టార్ APQ వ్యాసార్ధం, r = 12 సెం.మీ.
సెక్టార్ APQ వైశాల్యం

షేడ్ చేయవలసిన ప్రాంతం 4 × ఒక్కొక్క సెక్టార్ వైశాల్యం
= 4 × 113.14 = 452.56 చ. సెం.మీ.

ప్రశ్న9.
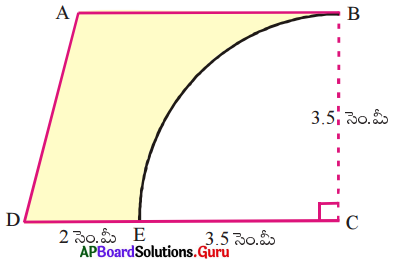
క్రింది పటములో ABCD ఒక సమలంబ చతుర్భుజం AB || CD మరియు ∠BCD = 90° మరియు పావు భాగము వృత్తము తొలగించబడినది. AB = BC = 3.5 సెం.మీ॥ మరియు DE = 2 సెం.మీ. అయిన మిగిలిన ప్రాంతము యొక్క వైశాల్యమును కనుగొనుము.
(π = \(\frac {22}{7}\)గా తీసుకోండి)

సాధన.
ABCD ఒక సమలంబ చతుర్భుజం
AB || CD
∠BCD = 90°
AB = BC = 3.5 సెం.మీ.; DE = 2 సెం.మీ.

సమలంబ చతుర్భుజం ABCD వైశాల్యం:
సమాంతర భుజాల పొడవులు, AB = 3.5 సెం.మీ.
CD = DE + EC
= 2 + 3.5 = 5.5 సెం.మీ.
సమాంతర భుజాల మధ్య దూరం, BC = 3.5 సెం.మీ.
∴ సమలంబ చతుర్భుజం వైశాల్యం

పావు వృత్తం EBC వైశాల్యం:
పావు వృత్త వ్యాసార్ధం, r = 3.5 సెం.మీ.

సమలంబ చతుర్భుజం నుంచి పావు వృత్తంను తొలగించగా మిగిలిన ప్రాంత వైశాల్యం = సమలంబ చతుర్భుజ వైశాల్యం – పావువృత్త వైశాల్యం
= 15.75 – 9.625 = 6.125 చ.సెం.మీ.

ప్రశ్న10.
ఒక దీర్ఘచతురస్రాకార పొలములో ఒక గుర్రము కట్టబడి ఉన్నది. దీర్ఘచతురస్ర కొలతలు 70 మీ మరియు 52 మీ కలిగియున్నది. దీర్ఘచతురస్రాకార పొలములో ఒక మూలలో 21 మీ. పొడవు కలిగిన ఒక తాడుకి గుర్రము కట్టబడియున్నది. అయిన గుర్రము కదలగలిగే ప్రాంత వైశాల్యము కనుగొనుము.

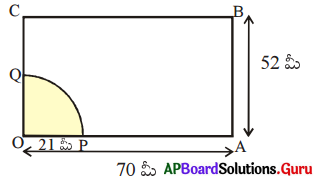
సాధన.
గుర్రం కదలగలిగే ప్రాంతం ఒక సెక్టారును సూచిస్తున్నది.
సెక్టార్ OPQ కోణం, x = 90°
సెక్టార్ OPQ వ్యాసార్ధం, r = 21 మీ.
సెక్టార్ OPQ వైశాల్యం

∴ గుర్రం కదలగలిగే ప్రాంత వైశాల్యం = 346.5 చ.మీ