AP Board 8th Class Maths Solutions Chapter 9 సమతల పటముల వైశాల్యములు Ex 9.1

SCERT AP 8th Class Maths Solutions Chapter 9 సమతల పటముల వైశాల్యములు Ex 9.1 Textbook Exercise Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 9th Lesson సమతల పటముల వైశాల్యములు Exercise 9.1

ప్రశ్న1.
సూచించిన విధముగా ఇచ్చిన ఆకృతులను విభజించండి.
(i) మూడు దీర్ఘచతురస్రాలు
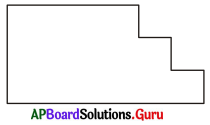
AP Board 8th Class Maths Solutions Chapter 9 సమతల పటముల వైశాల్యములు Ex 9.1 1
సాధన.

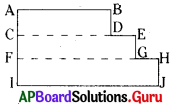
దీర్ఘ చతురస్రం ABCD
దీర్ఘ చతురస్రం CEFG
దీర్ఘ చతురస్రం FHIJ

(ii) మూడు దీర్ఘచతురస్రాలుగా
AP Board 8th Class Maths Solutions Chapter 9 సమతల పటముల వైశాల్యములు Ex 9.1 3
సాధన.

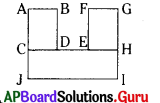
దీర్ఘ చతురస్రం ABCD
దీర్ఘ చతురస్రం EFGH
దీర్ఘ చతురస్రం CHUJ

(iii) రెండు సమలంబ చతుర్భుజాలుగా
AP Board 8th Class Maths Solutions Chapter 9 సమతల పటముల వైశాల్యములు Ex 9.1 5
సాధన.

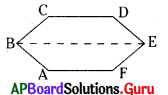
సమలంబ చతుర్భుజం ABEF
సమలంబ చతుర్భుజం BCDE

(iv) రెండు త్రిభుజాలు మరియు దీర్ఘచతురస్రము
AP Board 8th Class Maths Solutions Chapter 9 సమతల పటముల వైశాల్యములు Ex 9.1 7
సాధన.

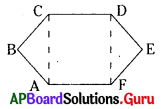
త్రిభుజం ABC
త్రిభుజం DEF
దీర్ఘచతురస్రం ACDF

(v) మూడు త్రిభుజాలుగా
AP Board 8th Class Maths Solutions Chapter 9 సమతల పటముల వైశాల్యములు Ex 9.1 9
సాధన.

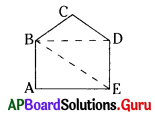
త్రిభుజం BCD
త్రిభుజం BDE
త్రిభుజం AEB

ప్రశ్న2.
ఈ క్రింది పటములు యొక్క వైశాల్యములను కనుగొనుము.
i)
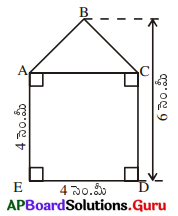
AP Board 8th Class Maths Solutions Chapter 9 సమతల పటముల వైశాల్యములు Ex 9.1 11
సాధన.
పంచభుజి ABCDE వైశాల్యం = చతురస్రం ACDE వైశాల్యం + త్రిభుజం ABC వైశాల్యం
చతురస్రం ACDE వైశాల్యం:
చతురస్రం ACDE వైశాల్యం = భుజం × భుజం
= ED × DC
= 4 × 4 = 16 చ.సెం.మీ

త్రిభుజం ABC వైశాల్యం:
పై పటం నుంచి BF = 6 – 4 = 2 సెం.మీ
Δ ABC వైశాల్యం = \(\frac {1}{2}\) × భూమి × ఎత్తు
= \(\frac {1}{2}\) × AC × BF
AP Board 8th Class Maths Solutions Chapter 9 సమతల పటముల వైశాల్యములు Ex 9.1 12
∴ పంచభుజి ABCDE వైశాల్యం, = చతురస్రం ACDE వైశాల్యం + ΔACB వైశాల్యం
= 16 + 4 = 20 చ.సెం.మీ

(ii)
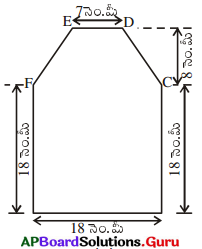
AP Board 8th Class Maths Solutions Chapter 9 సమతల పటముల వైశాల్యములు Ex 9.1 13
సాధన.
షడ్భుజి ABCDEF వైశాల్యం = చతురస్రం ABCF వైశాల్యం + సమలంబ చతుర్భుజం FCDE వైశాల్యం
చతురస్రం ABCF వైశాల్యం:
చతురస్రం ABCF వైశాల్యం = భుజం × భుజం
= AB × BC
= 18 × 18
= 324 చ.సెం.మీ
సమలంబ చతుర్భుజం FCDE వైశాల్యం
= \(\frac {1}{2}\) × h(a + b)
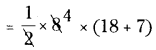
AP Board 8th Class Maths Solutions Chapter 9 సమతల పటముల వైశాల్యములు Ex 9.1 14
= 4(25) = 100 చ. సెం.మీ
∴ షడ్భుజి ABCDEF వైశాల్యం = చతురస్రం ABCF వైశాల్యం + సమలంబ చతుర్భుజం FCDE వైశాల్యం
= 324 + 100
= 424 చ.సెం.మీ

(iii)
AP Board 8th Class Maths Solutions Chapter 9 సమతల పటముల వైశాల్యములు Ex 9.1 15
సాధన.
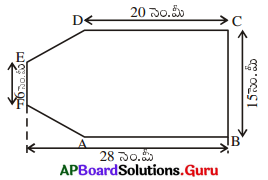
షడ్భుజి ABCDEF వైశాల్యం = దీర్ఘచతురస్రం ABCD వైశాల్యం + సమలంబ చతుర్భుజం ADEF వైశాల్యం
దీర్ఘచతురస్రం ABCD వైశాల్యం:
దీర్ఘచతురస్రం ABCD వైశాల్యం
= పొడవు × వెడల్పు
= AB × BC
= 20 × 15 = 300 చ.సెం.మీ

సమలంబ చతుర్భుజం ADEF వైశాల్యం:
పై పటం నుంచి సమాంతర భుజాలు \(\overline{\mathrm{AD}}, \overline{\mathrm{EF}}\) ల మధ్య దూరం, h = 28 – 20 = 8 సెం.మీ AD, a = 15 సెం.మీ ; EF, b = 6 సెం.మీ.
∴ సమలంబ చతుర్భుజం ADEF వైశాల్యం
= \(\frac {1}{2}\) × h(a + b)

= 4(21) = 84 చ.సెం.మీ .
షడ్భుజి ABCDEF వైశాల్యం = దీర్ఘ చతురస్రం ABCD వైశాల్యం + సమలంబ చతుర్భుజం ADEF వైశాల్యం
= 300 + 84 = 384 చ. సెం.మీ

ప్రశ్న3.
ABCD చతుర్భుజములో కర్ణము AC = 10 సెం.మీ మరియు AC పై శీర్షములు B మరియు D నుండి గీచిన లంబములు 5 సెం.మీ మరియు 6 సెం.మీ. పొడవులు కలిగియుంటే ABCD చతుర్భుజము యొక్క వైశాల్యమును కనుగొనుము.
సాధన.
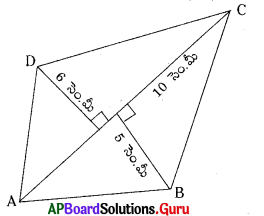
AP Board 8th Class Maths Solutions Chapter 9 సమతల పటముల వైశాల్యములు Ex 9.1 17
ABCD చతుర్భుజంలో కర్ణం AC, d = 10 సెం.మీ
B నుండి కర్ణం AC పై గీయబడిన లంబం h₁ = 5 సెం.మీ.
D నుండి కర్ణం AC పై గీయబడిన లంబం h₂ = 6 సెం.మీ
AP Board 8th Class Maths Solutions Chapter 9 సమతల పటముల వైశాల్యములు Ex 9.1 18

ప్రశ్న4.
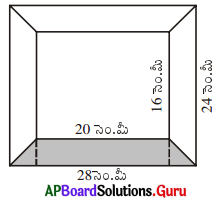
క్రింది పటములో చూపబడిన ఫోటో ఫ్రేము యొక్క బయటి అంచుకొలతలు 28 సెం.మీ × 24 సెం.మీ మరియు లోపలి అంచు కొలతలు 20 సెం.మీ × 16 సెం.మీ. ఫ్రేమ్ వెడల్పు ఏకరీతిగా యున్నచో షేడ్ చేయబడిన ప్రాంత వైశాల్యమును కనుగొనుము.
AP Board 8th Class Maths Solutions Chapter 9 సమతల పటముల వైశాల్యములు Ex 9.1 19
సాధన.

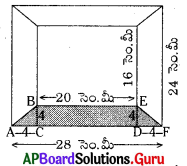
ఫోటో ఫ్రేము బయటి అంచు కొలతలు = 28 సెం.మీ × 24 సెం.మీ
బయటి అంచు పొడవు = 28 సెం.మీ
బయటి అంచు వెడల్పు = 24 సెం.మీ
లోపలి అంచు కొలతలు = 20 సెం.మీ × 16 సెం.మీ
లోపలి అంచు పొడవు = 20 సెం.మీ
లోపలి అంచు వెడల్పు = 16 సెం.మీ
త్రిభుజం ABC వైశాల్యం = \(\frac {1}{2}\) × భూమి × ఎత్తు
= \(\frac {1}{2}\) × AC × CB
AP Board 8th Class Maths Solutions Chapter 9 సమతల పటముల వైశాల్యములు Ex 9.1 21
దీర్ఘచతురస్రం CDEB వైశాల్యం = పొడవు × వెడల్పు
= CD × DE
= 20 × 4
= 80 చ.సెం.మీ
త్రిభుజం DEF వైశాల్యం = \(\frac {1}{2}\) × భూమి × ఎత్తు
= \(\frac {1}{2}\) × DF × DE
AP Board 8th Class Maths Solutions Chapter 9 సమతల పటముల వైశాల్యములు Ex 9.1 22
= 8 చ.సెం.మీ
∴ షేడ్ చేయబడిన ప్రాంత వైశాల్యం = త్రిభుజం ABC వైశాల్యం + దీర్ఘచతురస్రం CDEB వైశాల్యం + త్రిభుజం DEF వైశాల్యం
= 8 + 80 + 8
= 96 చ.సెం.మీ

ప్రశ్న5.
ఈ క్రింది ఇవ్వబడిన పొలముల యొక్క వైశాల్యములను కనుగొనుము. కొలతలన్నియూ మీటర్లలో యున్నవి.
i)
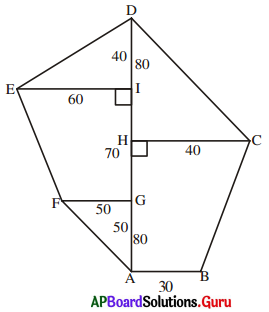
AP Board 8th Class Maths Solutions Chapter 9 సమతల పటముల వైశాల్యములు Ex 9.1 23
సాధన.
సమలంబ చతుర్భుజం ABCH వైశాల్యం
= \(\frac {1}{2}\) × h(a + b)

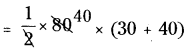
= 40 (70) = 2800 చ.మీ
త్రిభుజం HCD వైశాల్యం = \(\frac {1}{2}\) × HC x HD

= 1600 చ.మీ
త్రిభుజం EID వైశాల్యం = \(\frac {1}{2}\) × EI × ID

= 1200 చ.మీ
సమలంబ చతుర్భుజం FGIE వైశాల్యం
= \(\frac {1}{2}\) × h(a + b)
AP Board 8th Class Maths Solutions Chapter 9 సమతల పటముల వైశాల్యములు Ex 9.1 27
= 35 (110) = 3850 చ.మీ
త్రిభుజం FGA వైశాల్యం = \(\frac {1}{2}\) × FG × GA

= 1250 చ.మీ
∴ పొలం వైశాల్యం = సమలంబ చతుర్భుజం ABCH వైశాల్యం + త్రిభుజం HCD వైశాల్యం + త్రిభుజం EID వైశాల్యం + సమలంబ చతుర్భుజం FGIE వైశాల్యం + త్రిభుజం FGA వైశాల్యం
= 2800 + 1600 + 1200 + 3850 + 1250
= 10700 చ.మీ

(ii)
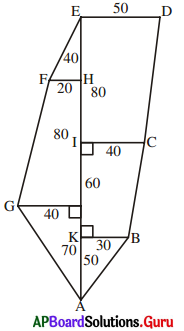
AP Board 8th Class Maths Solutions Chapter 9 సమతల పటముల వైశాల్యములు Ex 9.1 29
సాధన.
త్రిభుజం ABK వైశాల్యం = \(\frac {1}{2}\) × KB × KA

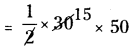
= 750 చ.మీ
సమలంబ చతుర్భుజం KBCI వైశాల్యం
= \(\frac {1}{2}\) × h(a + b)

= 30 (70) = 2100 చ.మీ
సమలంబ చతుర్భుజం ICDE వైశాల్యం
= \(\frac {1}{2}\) × h(a + b)

= 40(90)
= 3600 చ.మీ
త్రిభుజం FHE వైశాల్యం = \(\frac {1}{2}\) × FH × HE
AP Board 8th Class Maths Solutions Chapter 9 సమతల పటముల వైశాల్యములు Ex 9.1 33
= 400 చ.మీ
సమలంబ చతుర్భుజం GJHF వైశాల్యం
= \(\frac {1}{2}\) × h(a + b)

= 40 (60) = 2400 చ.మీ
త్రిభుజం GJA వైశాల్యం = \(\frac {1}{2}\) × GJ × JA

= 1400 చ.మీ
∴ పొలం వైశాల్యం = ΔKBA వైశాల్యం + సమలంబ చతుర్భుజం KBCI వైశాల్యం + సమలంబ చతుర్భుజం ICDE వైశాల్యం + ΔFHE వైశాల్యం + సమలంబ చతుర్భుజం GJHF వైశాల్యం + ΔGJA వైశాల్యం
= 750 + 2100 + 3600 + 400 + 2400 + 1400
= 10650 చ.మీ

ప్రశ్న6.
సమలంబ చతుర్భుజంలోని సమాంతర భుజాల పొడవుల నిష్పత్తి 5 : 3 వాటి మధ్య దూరం 16 సెం.మీ. సమలంబ చతుర్భుజం యొక్క వైశాల్యము 960 చ. సెం.మీ అయిన సమాంతర భుజముల పొడవులను కనుగొనుమ.
సాధన.
సమలంబ చతుర్భుజంలోని సమాంతర భుజాల పొడవుల నిష్పత్తి = 5 : 3
∴ సమాంతర భుజాల పొడవులు = 5x, 3x
∴ a = 5x, b = 3x
సమాంతర భుజాల మధ్య దూరం, h = 16 సెం.మీ.
సమలంబ చతుర్భుజ వైశాల్యం
= \(\frac {1}{2}\) × h(a + b)

= 8 (8x) = 64 x
లెక్క ప్రకారం, సమలంబ చతుర్భుజ వైశాల్యం = 960 చ.సెం.మీ
∴ 64x = 960
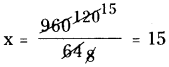
AP Board 8th Class Maths Solutions Chapter 9 సమతల పటముల వైశాల్యములు Ex 9.1 37
x = 15
∴ సమాంతర భుజాల పొడవులు,
a = 5x = 5 × 15 = 75 సెం.మీ
b = 3x = 3 × 15 = 45 సెం.మీ

ప్రశ్న7.
ఒక భవనము యొక్క నేల 3000 టైల్స్ చే కప్పబడినది. ప్రతి టైల్ సమచతుర్భుజ ఆకృతిని కలిగియుండి కర్ణముల పొడవులు 45 సెం.మీ, 30 సెం.మీలు కలిగియున్నది. ప్రతీ టైల్ యొక్క వెల చదరపు మీటరుకు 20 రూపాయలు అయిన ఫ్లోరింగ్ నకు అయ్యే మొత్తము ఖర్చు ఎంత ?
సాధన.
ఒక భవనం యొక్క నేల 3000 టైల్స్ చే కప్పబడినది.
ప్రతి టైల్ సమచతుర్భుజం ఆకృతిని కలిగియున్నది.
టైల్ యొక్క కర్ణముల పొడవులు,
d₁ = 45 సెం.మీ, d₂ = 30 సెం.మీ
ఒక్కొక్క టైల్ వైశాల్యం = \(\frac {1}{2}\)d₁d₂

= 675 చ.సెం.మీ
∴ భవనం యొక్క నేల వైశాల్యం = 3000 × 675 = 2025000 చ.సెం.మీ
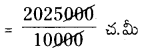
AP Board 8th Class Maths Solutions Chapter 9 సమతల పటముల వైశాల్యములు Ex 9.1 39
(∵ 1 చ.మీ. = 10000 చ.సెం.మీ)
= \(\frac {2025}{10}\) చ.మీ = 202.5 చ.మీ
టైల్ యొక్క చదరపు మీటరు ఖరీదు = ₹ 20
∴ ఫ్లోరింగ్ నకు అయ్యే మొత్తం ఖర్చు = ₹ 202.5 × 20 = ₹ 4050

ప్రశ్న8.
ఈ క్రింద పంచభుజి ఆకృతిలో యున్న పటం యివ్వబడినది. దీని వైశాల్యమును కనుగొనేందుకు జ్యోతి మరియు రషీదా దానిని రెండు వేర్వేరు విధాలుగా విభజించారు. అయిన రెండు విధాలుగా పంచభుజి వైశాల్యం కనుగొనండి. దాని నుండి ఏమి గమనించారు?
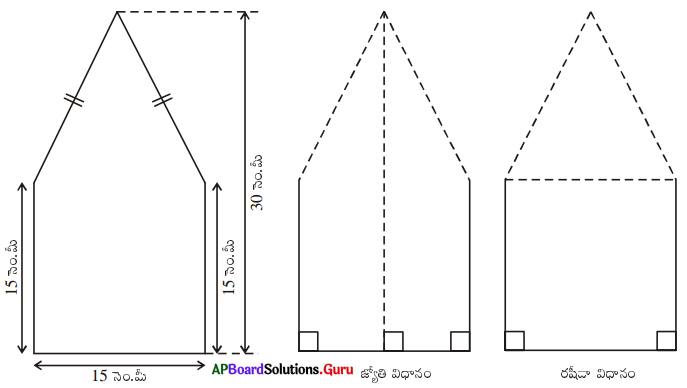
AP Board 8th Class Maths Solutions Chapter 9 సమతల పటముల వైశాల్యములు Ex 9.1 40
సాధన.
జ్యోతి విధానం :

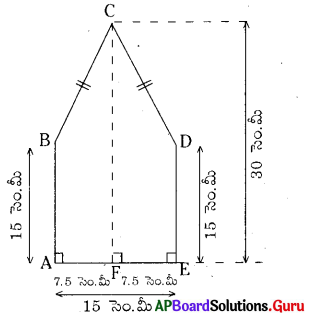
సమలంబ చతుర్భుజం ABCF వైశాల్యం:
సమాంతర భుజాల పొడవులు, FC, a = 30 సెం.మీ.
AB, b = 15 సెం.మీ.
సమాంతర భుజాలు \(\overline{\mathrm{FC}}, \overline{\mathrm{AB}}\)ల మధ్య దూరం, h = 7.5 సెం.మీ.
సమలంబ చతుర్భుజం ABCF వైశాల్యం
= \(\frac {1}{2}\)h(a + b)
= \(\frac {1}{2}\) × 7.5 (30 + 15)
AP Board 8th Class Maths Solutions Chapter 9 సమతల పటముల వైశాల్యములు Ex 9.1 42
= 168.75 చ.సెం.మీ
సమలంబ చతుర్భుజం FEDC వైశాల్యం:
సమాంతర భుజాల పొడవులు, FC, a = 30 సెం.మీ.
ED, b = 15 సెం.మీ.
సమాంతర భుజాలు \(\overline{\mathrm{FC}}, \overline{\mathrm{ED}}\)ల మధ్య దూరం, h = 7.5 సెం.మీ.
సమలంబ చతుర్భుజం FEDC వైశాల్యం
= \(\frac {1}{2}\)h(a + b)
= \(\frac {1}{2}\) × 7.5 (30 + 15)
AP Board 8th Class Maths Solutions Chapter 9 సమతల పటముల వైశాల్యములు Ex 9.1 43
= 168.75 చ.సెం.మీ
∴ పంచభుజి ABCDE వైశాల్యం = సమలంబ చతుర్భుజం ABCF వైశాల్యం + సమలంబ చతుర్భుజం FEDC వైశాల్యం
= 168.75 + 168.75
= 337.50 చ.సెం.మీ

రషీదా విధానం :
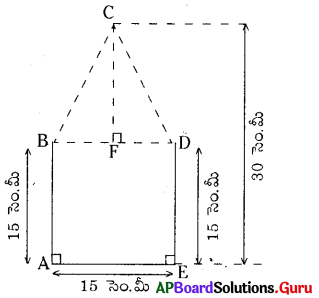
AP Board 8th Class Maths Solutions Chapter 9 సమతల పటముల వైశాల్యములు Ex 9.1 44
చతురస్రం ABDE వైశాల్యం = భుజం × భుజం
= AE × ED
= 15 × 15
= 225 చ.సెం.మీ.
త్రిభుజం BDC వైశాల్యం = \(\frac {1}{2}\) × భూమి × ఎత్తు
= \(\frac {1}{2}\) × BD × CF
= \(\frac {1}{2}\) × 15 × 15
(∵ CF = 30 – 15 సెం.మీ)
= \(\frac {225}{2}\)
= 112.50 చ.సెం.మీ
∴ పంచభుజి ABCDE వైశాల్యం = చతురస్రం ABDE వైశాల్యం + త్రిభుజం BDC వైశాల్యం
= 225 + 112.50
= 337.500 చ.సెం.మీ
పంచభుజిని ఎన్ని విధాలుగా విభజించి చేసినా దాని వైశాల్యం మారదు. కచ్చితంగా చెప్పాలంటే ఏ బహుభుజినైనా ఎన్ని విధాలుగా విభజించి చేసినా దాని వైశాల్యం మారదు.