AP State Syllabus AP Board 8th Class Maths Solutions Chapter 6 Square Roots and Cube Roots Ex 6.3 Textbook Questions and Answers.
AP State Syllabus 8th Class Maths Solutions 6th Lesson Square Roots and Cube Roots Exercise 6.3
![]()
Question 1.
Find the square roots of the following numbers by division method.
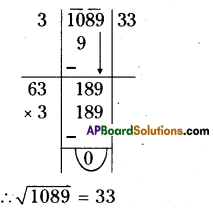
(i) 1089
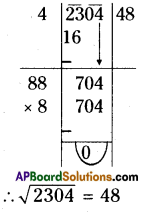
(ii) 2304
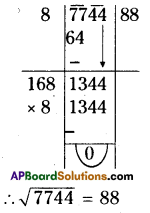
(iii) 7744
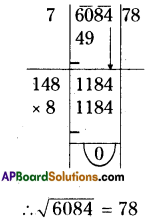
(iv) 6084
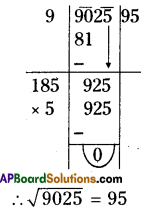
(v) 9025
Solution:
(i) 1089
(ii) 2304
![]()
(iii) 7744
(iv) 6084
(v) 9025
![]()
Question 2.
Find the square roots of the following decimal numbers.
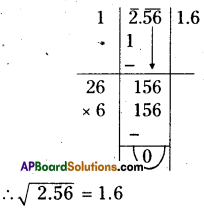
(i) 2.56
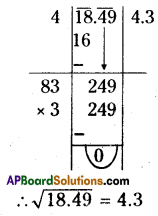
(ii) 18.49
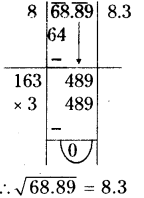
(iii) 68.89
(iv) 84.64
Solution:
(i) 2.56
(ii) 18.49
![]()
(iii) 68.89
(iv) 84.64
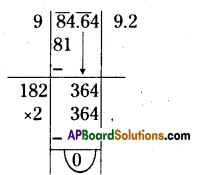
Question 3.
Find the least number that is to be subtracted from 4000 to make it perfect square
Solution:
Square root of 4000 by
Division Method:
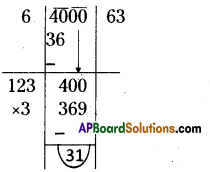
∴ The least number 31 should be subtracted from 4000 we will get a perfect square number4
∴ 4000 – 31 = 3969
= [latex]\sqrt{3969}=\sqrt{63 \times 63}[/latex] = 63
![]()
Question 4.
Find the length of the side of a square whose area is 4489 sq.cm.
Solution:
Area of a square (A) = 4489 sq.cms
A = s2
s2 = 4489
s = [latex]\sqrt{4489}=\sqrt{67 \times 67}[/latex] = 67cms.
∴ The side of a square (s) = 67cms.
Question 5.
A gardener wishes to plant 8289 plants in the form of a square and found that there were 8 plants left. How many plants were planted in each row?
Solution:
No. of plants are planted = 8289 If 8289 plants are planted in a square shape, 8 plants are left.
Then remaining plants = 8289 – 8 = 8281
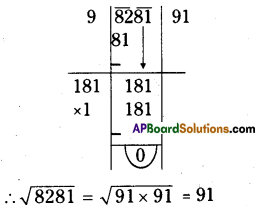
∴ No. of plants for each row = 91
∴ 8281 plants are planted in a square shape then no. of plants are planted for each row = 91
![]()
Question 6.
Find the least perfect square with four digits.
Solution:
The smallest number of 4 digits = 1000
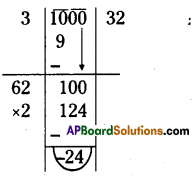
∴ 24 should be added tö 1000 then 1000 + 24 = 1024
∴ The smallest 4 digited perfect square number is 1024.
[∵ [latex]\sqrt{1024}[/latex] = 32]
![]()
Question 7.
Find the least number which must be added to 6412 to make it a perfect square?
Solution:
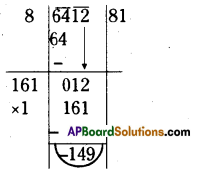
∴ The least number 149 should be added to 6412 then we will get a perfect square number.
∴ 6412 + 149 = 6561
∴ [latex]\sqrt{6561}=\sqrt{81 \times 81}[/latex] = 81
Question 8.
Estimate the value of the following numbers to the nearest whole number
(i) [latex]\sqrt{97}[/latex]
(ii) [latex]\sqrt{250}[/latex]
(iii) [latex]\sqrt{780}[/latex]
Solution:
ï) [latex]\sqrt{97}[/latex] , 97 lie between the perfect
square numbers 81 and 100.
∴ 81 <97< 100
92 < 97 < 102
=9 < [latex]\sqrt{97}[/latex] < 10
∴ [latex]\sqrt{97}[/latex] Is nearest to 10.
[∵ 97 is nearest to 100]
(ii) [latex]\sqrt{250}[/latex], 250 lie between the perfect square numbers 225 and 256.
∴ 225 < 250 < 256
152 < 250 < 162
= 15 < [latex]\sqrt{250}[/latex] <16
∴ [latex]\sqrt{250}[/latex] is nearest to 16.
[ ∵ 250 is nearest to 256]
![]()
ii) [latex]\sqrt{780}[/latex], 780 lie between the perfect
square numbers 729 and 784.
∴ 729 < 780 < 784
272 < 780 < 282
= 27< [latex]\sqrt{780}[/latex] <28
∴ [latex]\sqrt{780}[/latex] is nearest to 28.
[ ∵ 780 is nearest to 784]