AP State Syllabus AP Board 8th Class Maths Solutions Chapter 6 Square Roots and Cube Roots Ex 6.2 Textbook Questions and Answers.
AP State Syllabus 8th Class Maths Solutions 6th Lesson Square Roots and Cube Roots Exercise 6.2
Question 1.
Find the square roots of the following numbers by Prime factorization method.
(1) 441
(ii) 784
(iii) 4096
(iv) 7056
Solution:
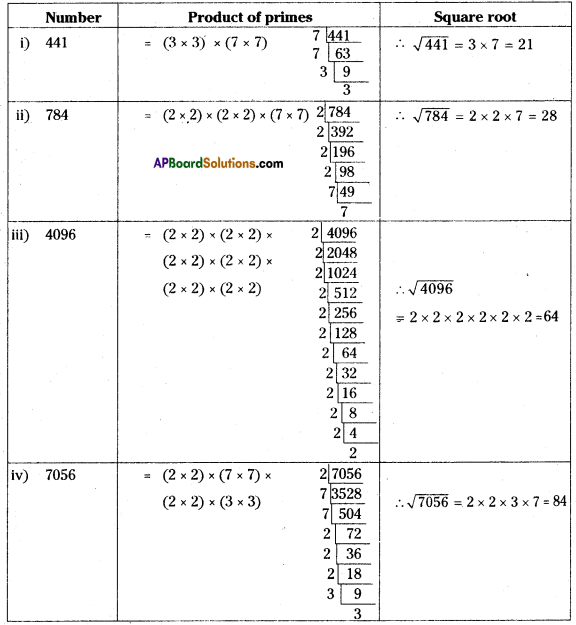
Question 2.
Find the smallest number by which 3645 must be multiplied to get a perfect square.
Solution:
The prime factorization of 3645
= (3 × 3) × (3 × 3) (3 × 3) × 5
∴ Deficiency of one ‘5’ is appeared in the above product.
∴ 3645 is multiplied with 5 then we will get a perfect square.
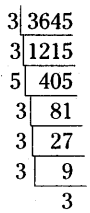
Question 3.
Find the smallest number by which 2400 is to be multiplied to get a perfect square and also find the square root of the resulting number.
Solution:
The prime factorization of 2400
=(2 × 2) × (2 × 2) × 2 × (5 × 5) × 3
∴ 2,3 are needed to form a pair
∴ 2 × 3 = 6
∴ 6 should be multiplied with 2400 then we will get a perfect square number.
∴ 2400 × 6 = 14400
∴ \(\sqrt{14400}\) = 120
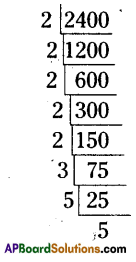
Question 4.
Find the smallest number by which 7776 is to be divided to get a perfect square.
Solution:
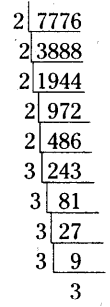
The prime factorization of 7776
=(2 × 2) × (2 × 2) × 2 × (3 × 3) × (3 × 3) × 3
∴ 2, 3 are needed to form a pair
∴ 2 × 3 = 6
∴ 7776 should be divided by 6 then we will get a perfect square number.
Question 5.
1521 trees are planted in a garden in such a way that there are as many trees in each row as there are rows in the garden. Find the number of rows and number of trees in each row.
Solution:
Let the no. of trees planted in a garden for each row = x say.
No. of rows in the garden = x
∴ Total no. of trees in the garden = x × x = x2
According to the sum x2 = 1521
x = \(\sqrt{1521}=\sqrt{39 \times 39}\) = 39
∴ No. of trees for each row = 39
No. of rows in the garden = 39
Question 6.
A school collected ₹ 2601 as fees from its students. If fee paid by each student and number students in the school were equal, how many students were there in the school?
Solution:
Let the no. of students in a school = x say
The (amount) fee paid by each student = ₹ x
Amount collected by all the students
= x × x = x2
According to the sum
∴ x2 = 2601
x = \(\sqrt{2601}=\sqrt{51 \times 51}\) = 51
∴ x = 51
∴ No. of students in the school = 51
Question 7.
The product of two numbers is 1296. If one number is 16 times the other, find the two numbers?
Solution:
Given that the product of two numbers = 1296.
Let the second number = x say
Then first number = 16 × x = 16x
∴ The product of two numbers
= x × 16x= 16x2
According to the sum
16x2 = 1296
⇒ x2 = \(\frac { 1296 }{ 16 }\) = 81
⇒ x2 = 81
⇒ x = \(\sqrt{8} \overline{1}=\sqrt{9 \times 9}\) = 9
⇒ x = 9
∴ The first number = 16x
= 16 × 9
=144
The second number = x = 9
Question 8.
7921 soldiers sat in an auditorium in such a way that there are as many soldiers in a row as there are rows in the auditorium. How many rows are there in the auditorium’?
Solution:
Let the number of soldiers sat in an auditorium for each row = x say
∴ No. of rows in an auditorium = x
∴ Total no. of soldiers = x × x = x2
According to the sum,
x2 = 7921
x = \(\sqrt{7921}=\sqrt{89 \times 89}\) = 89
∴ No. of rowS in an auditorium = 89
Question 9.
The area of a square field is 5184 m2. Find the area of a rectangular field, whose perimeter is equal to the perimeter of the square field and whose length is twice of its breadth.
Solution:
Area of a square field = 5184 m2
A = s2 = 5184
:. s = \(\sqrt{5184}=\sqrt{72 \times 72}\) = 72
∴ s = 72
∴ Perimeter of the square field = 4 × s
= 4 × 72
= 288 m
According to the sum,
Perimeter of a rectangular field
= Perimeter of a square field = 288 m
Let the breadth of a rectangular field
= x m say
∴ Length = 2 × x = 2 × m
∴ Perimeter of the rectangular field
= 2 (1 + b)
= 2 (2x + x)
= 2 × 3x
= 6x
∴ 6x = 288 .
x = \(\frac { 288 }{ 6 }\)
x = 48
∴ Breadth of the rectangular field
= x = 48 m
Length of the rectangular field = 2x
= 2 × 48
=96m
∴ Area of the rectangular field
= l × b
= 96 × 48
= 4608 m2