AP Board 8th Class Maths Solutions Chapter 1 Rational Numbers Ex 1.1

AP State Syllabus AP Board 8th Class Maths Solutions Chapter 1 Rational Numbers Ex 1.1 Textbook Questions and Answers.

AP State Syllabus 8th Class Maths Solutions 1st Lesson Rational Numbers Exercise 1.1

Question 1.
Name the properly Involved in the following examples.

vii) 7a + (-7) = 0
viii) x + [latex]\frac{1}{x}[/latex] = 1(x ≠ 0)
ix) (2 x x) + (2 x 6) = 2 x (x + 6)
Solution:
i) Additive identity
ii) Distributive law
iii) Multiplicative identity
iv) Multiplicative identity
v) Commutative law of addition
vi) Closure law in multiplication
vii) Additive inverse
viii) Multiplicative inverse
ix) Distributive

Question 2.
Write the additive and the multiplicative inverses of the following.
i) [latex]\frac{-3}{5}[/latex]
ii) 1
iii) 0
iv) [latex]\frac{7}{9}[/latex]
v) -1
Solution:

Question 3.
Fill in the blanks



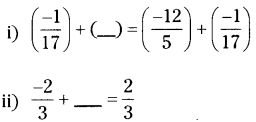
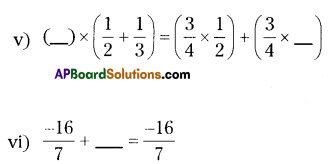
Solution:
i) [latex]\left(\frac{-12}{5}\right)[/latex]
ii) [latex]\left(\frac{4}{3}\right)[/latex]
iii) [latex]\left(\frac{9}{11}\right)[/latex]
iv) [latex]\left(\frac{6}{7}\right)[/latex]
v) [latex]\left(\frac{3}{4}, \frac{1}{3}\right)[/latex]
vi) 0

Question 4.
Multiply [latex]\frac{2}{11}[/latex] by the reciprocal of [latex]\frac{-5}{14}[/latex]
Solution:
The reciprocal of [latex]\frac{-5}{14}[/latex] is [latex]\frac{-14}{5}[/latex]
( ∵ [latex]\left(\frac{-5}{14}\right) \times\left(\frac{-14}{5}\right)=1[/latex] )
∴ The product of [latex]\frac{2}{11}[/latex] and [latex]\frac{-14}{5}[/latex] is
[latex]\frac{2}{11} \times\left(\frac{-14}{5}\right)=\frac{-28}{55}[/latex]

Question 5.
Which properties can be used computing [latex]\frac{2}{5} \times\left(5 \times \frac{7}{6}\right)+\frac{1}{3} \times\left(3 \times \frac{4}{11}\right)[/latex]
Solution:
The following properties are involved in the product of
[latex]\frac{2}{5} \times\left(5 \times \frac{7}{6}\right)+\frac{1}{3} \times\left(3 \times \frac{4}{11}\right)[/latex]
i) Multiplicative associative property.
ii) Multiplicative inverse.
iii) Multiplicative identity.
iv) Closure with addition

Question 6.
Verify the following
[latex]\left(\frac{5}{4}+\frac{-1}{2}\right)+\frac{-3}{2}=\frac{5}{4}+\left(\frac{-1}{2}+\frac{-3}{2}\right)[/latex]
Solution:

Question 7.
Evaluate [latex]\frac{3}{5}+\frac{7}{3}+\left(\frac{-2}{5}\right)+\left(\frac{-2}{3}\right)[/latex] after rearrangement.
Solution:

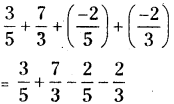
Let x = [latex]1.2 \overline{4}[/latex]
⇒ x = 1.244……. …………………(1)
Here periodicity of equation (1) is 1. So
it should be multiplied by 10 on both
sides.
⇒ 10 x x = 10 x 1.244
10x = 12.44 …………..(2)

Question 8.
Subtract
(i) [latex]\frac{3}{4}[/latex] from [latex]\frac{1}{3}[/latex]
(ii) [latex]\frac{-32}{13}[/latex] from 2
(iii) -7 from [latex]\frac{-4}{7}[/latex]
Solution:

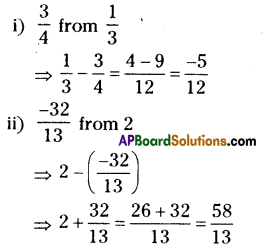
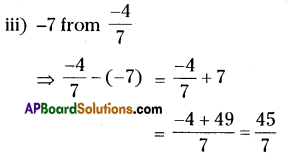
Question 9.
What numbers should be added to [latex]\frac{-5}{8}[/latex] so as to get [latex]\frac{-3}{2}[/latex] ?
Solution:
Let the number to be add ‘x’ say

∴ [latex]\frac{-7}{8}[/latex] should be added to [latex]\frac{-5}{8}[/latex] then we will get [latex]\frac{-3}{2}[/latex]

Question 10.
The sum of two rational numbers is 8 If one of the numbers is [latex]\frac{-5}{6}[/latex] find the other.
Let the second number be ‘x’ say
⇒ [latex]x+\left(\frac{-5}{6}\right)=8[/latex]
⇒[latex]8+\frac{5}{6}=\frac{48+5}{6}=\frac{53}{6}[/latex]
∴ The other number (x) = [latex]\frac{53}{6}[/latex]

Question 11.
Is subtraction associative in rational numbers? Explain with an example.
Solution:
Let [latex]\frac{1}{2}, \frac{3}{4}, \frac{-5}{4}[/latex] are any 3 rational numbers.
Associative property under subtraction
a – (b – c) = (a – b) – c

∴ L.H.S. ≠ R.H.S.
∴ a – (b – c) ≠ (a – b) – c
∴ Subtraction is not an associative in rational numbers.

Question 12.
Verify that – (-x) = x for
(i) x = [latex]\frac{2}{15}[/latex]
(ii) x = [latex]\frac{-13}{15}[/latex]
Solution:

Question 13.
Write-
(i) The set of numbers which do not have any additive identity
(ii) The rational number that does not have any reciprocal
(iii) The reciprocal of a negative rational number.
Solution:
i) Set of natural numbers ’N’ doesn’t possesses the number ‘0’.
ii) The rational number ‘0’ has no multiplicative inverse.
[ ∵ 1/0 is not defined]
iii) The reciprocal of a negative rational number is a negative rational number.
Ex : Reciprocal of [latex]\frac{-2}{5}=\frac{-5}{2}[/latex]