AP State Syllabus AP Board 6th Class Maths Solutions Chapter 6 Basic Arithmetic InText Questions and Answers.
AP State Syllabus 6th Class Maths Solutions 6th Lesson Basic Arithmetic InText Questions
![]()
Check Your Progress (Page No. 84)
Question 1.
Express the terms 45 and 70 by using ratio symbol.
Solution:
Given terms are 45 and 70
Ratio = 45 : 70
It can be read as 45 is to 70.
Question 2.
Write antecedent in the ratio 7:15.
Solution:
Given ratio 7 : 15
In the ratio first term is called antecedent.
In 7 : 15 antecedent is 7.
Question 3.
Write the consequent in the ratio 8 : 13.
Solution:
Given ratio 8 : 13
In the ratio second term is called consequent.
In 8 : 13 consequent is 13.
![]()
Question 4.
Express the ratio 35 : 55 in the simplest form.
Solution:
Given ratio 35 : 55 (or)
To write the ratio in the simplest form we have to divide by the common factor of two terms 35 and 55.
Common factor is 5.
Now divide by 5,
[latex]\frac{35}{55}=\frac{35 \div 5}{55 \div 5}=\frac{7}{11}[/latex]
Simplest form of [latex][/latex] is [latex]\frac{7}{11}[/latex]
Question 5.
In the given figure, find the ratio of
i) Shaded part to unshaded parts.
ii) Shaded part to total parts,
iii) Unshaded parts to total parts.

Solution:
i) In the given figur.e,
Number of shaded parts = 1
Number of unshaded parts = 3
Ratio = shaded parts : unshaded parts = 1:3
ii) Number of shaded parts = 1
Total parts = 4
Ratio = shaded parts : total parts = 1:4
iii) Number of unshaded parts = 3
Total parts = 4
Ratio = unshaded parts : total parts = 3:4
Question 6.
Express the following in the form of ratio.
a) The length of a rectangle is triple its breadth. ‘
b) In a school, the workload of teaching 19 sections has been assigned to 38 teachers.
Solution:
a) Let breadth of rectangle = x or one part = 1 part
length of rectangle = triple the breadth
= 3 x x = 3x = 3 parts
Ratio = l : b = x : 3x =[latex]\frac{1 x}{3 x}=\frac{1}{3}[/latex] = 1:3
b) Given number of sections = 19
Number of teachers = 38
Ratio = 19 : 38 = [latex]\frac{19}{38}=\frac{1}{2}[/latex] = 1 : 2
![]()
(Page No. 88)
Question 1.
Which ratio is larger in the following pairs ?
(a) 5 : 4 or 9 : 8
(b) 12 : 14 or 16 : 18
(c) 8: 20 or 12: 15
(d)4:7 or 7:11
Solution:
a) 5 : 4 or 9 : 8
Write the given ratios as fractions, we have 5 : 4 = [latex]\frac{5}{4}[/latex] and 9 : 8 = [latex]\frac{9}{8}[/latex]
Now find the LCM of the denominators of 4 and 8 is 8.
Make the denominator of the each fraction equal to 8.
We have [latex]\frac{5}{4} \times \frac{2}{2}=\frac{10}{8}[/latex] and [latex]\frac{9}{8} \times \frac{1}{1}=\frac{9}{8}[/latex]
Clearly we know that 10 > 9
∴ [latex]\frac{10}{8}>\frac{9}{8}[/latex] (or) 10 : 8 > 9 : 8
10 : 8 is equal to 5 : 4
Therefore the larger ratio is 5 : 4.
b) 12 : 14 or 16:18
12 : 14 = [latex]\frac{12}{14}=\frac{6}{7}[/latex] and 16 : 18 = [latex]\frac{16}{18}=\frac{8}{9}[/latex]
Now find the LCM of the denominators of 7 and 9 is 63.
Make the denominator of the each fraction equal to 63.
we have [latex]\frac{6}{7} \times \frac{9}{9}=\frac{54}{63}[/latex] and [latex]\frac{8}{9} \times \frac{7}{7}=\frac{56}{63}[/latex]
Clearly, we know that 54 < 56
∴ [latex]\frac{54}{63}<\frac{56}{63}[/latex] (or) 54:63 < 56:63
56 : 63 is equal to 16 : 18 (or) 8 : 9
∴ The larger ratio is 16 : 18.
c) 8 : 20 or 12 : 15
Write the given ratios as fractions we have
8:20 = [latex]\frac{8}{20}=\frac{2}{5}[/latex] and 12:15 = [latex]\frac{12}{15}=\frac{4}{5}[/latex]
[latex]\frac{2}{5}[/latex] and [latex]\frac{4}{5}[/latex]
Clearly [latex]\frac{2}{5}[/latex] < [latex]\frac{4}{5}[/latex]
i.e., 2:5 < 4 : 5 (or) 8: 20 < 12: 15
Therefore the larger ratio is 12 : 15.
![]()
d) 4: 7 or 7: 11
Write the given ratios as fractions, we have 4 7
4 : 7 = [latex]\frac{4}{7}[/latex] and 7:11 = [latex]\frac{7}{11}[/latex] .
Now find the LCM of the denominators of 7 and 11 is 77.
Make the denominators of the each fraction equal to 77.
We have [latex]\frac{4}{7} \times \frac{11}{11}=\frac{44}{77}[/latex] and [latex]\frac{7}{11} \times \frac{7}{7}=\frac{49}{77}[/latex]
[latex]\frac{44}{7}[/latex] and [latex]\frac{49}{77}[/latex]
Clearly we know that 44 < 49
∴ [latex]\frac{44}{77}<\frac{49}{77}[/latex] (or) 44 : 77 < 49 : 77
i.e.,4: 7 < 7 : 11
Therefore the larger ratio is 7 : 11
Question 2.
Find three equivalent ratios of 12 : 16.
Solution:
Given ratio is 12 : 16
Write the given ratio as fraction we have 12:16= [latex]\frac{12}{16}=\frac{3}{4}[/latex]
Now, write equivalent fractions of [latex]\frac{3}{4}[/latex]
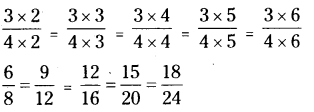
i. e., 6 : 8 = 9 : 12 = 12 : 16 = 15 : 20 = 18 : 24
∴ Equivalent ratios of 12 : 16 are 6 : 8, 9 : 12, 12 : 16, 15 : 20 and 18 : 24.
![]()
(Page No. 90)
Question 1.
Check whether the following terms are in proportion ?
1) 5,6,7,8
2) 3,5,6,10
3) 4,8,7,14
4) 2,12,3,18
Solution:
1) Given, 5, 6, 7, 8
If a, b, c, d are in proportion i.e., a : b :: c : d
If 5, 6, 7, 8 are in proportion i.e., 5 : 6 : : 7 : 8
We know that, product of extremes = Product of means [a x d : b x c]
5 x 8 = 6 x 7
40 ≠ 42
So, 5, 6, 7, 8 are not in proportion.
2) Given, 3, 5, 6, 10
If a, b, c, d are in proportion i.e., a : b :: c : d
If 3, 5, 6, 10 are in proportion i.e., 3 : 5 :: 6 : 10
We know that, product of extremes = Product of means a x d = b x c
3 x 10 = 5 x 6
30 = 30
So, 3, 5, 6, 10 are in proportion.
3) Given, 4, 8, 7, 14.
If a, b, c, d are in proportion i.e., a : b : : c : d
If 4, 8, 7, 14 are in proportion i.e., 4 : 8 : : 7 : 14
We know that, product of extremes = Product of means a x d = b x c
4 x 14 = 8 x 7
56 = 56
So, 4, 8, 7, 14 are in proportion.
4) Given, 2, 12, 3, 18
If a, b, c, d are in proportion i.e., a : b :: c : d
If 2, 12, 3, 18 are in proportion i.e., 2 : 12 : : 3 : 18
We know that, product of extremes = Product of means [ a x d = b x c ]
2 x 18 = 12 x 3
36 = 36
So, 2, 12, 3, 18 are in proportion.
![]()
Let’s Explore (Page No. 92)
Question 1.
Read the table and fill in the boxes.

Prepare two similar problems and ask your friend to solve them
Solution:
| Weight | Cost of Tomato | Cost of Potato |
| 5 kg | ₹ 75 | ₹ 60 |
| 1 kg | ₹15 | ₹ 12 |
| 3 kg | ₹ 45 | ₹ 36 |
(Page. No. 94)
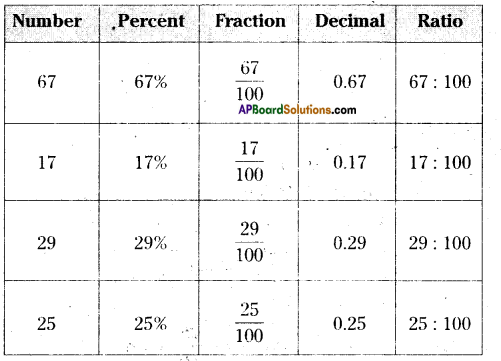
Question 1.
Represent the following in other forms.
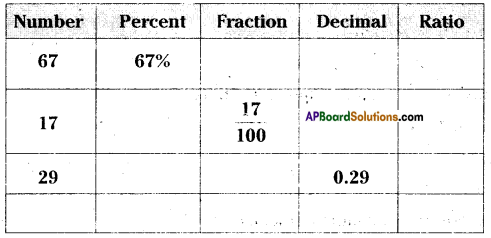
Solution: