SCERT AP 6th Class Maths Solutions Chapter 5 భిన్నాలు – దశాంశ భిన్నాలు InText Questions and Answers.
AP State Syllabus 6th Class Maths Solutions 5th Lesson భిన్నాలు – దశాంశ భిన్నాలు InText Questions
[పేజి నెం. 68]
3 × [latex]\frac {1}{5}[/latex] = [latex]\frac {1}{5}[/latex] × 3 అని చెప్పగలమా ?
సాధన.
అవును. 3 × [latex]\frac {1}{5}[/latex] = [latex]\frac {1}{5}[/latex] × 3 అనునది నిజం.
గుణకారంలో స్థిత్యంతర ధర్మాన్ని ఉపయోగించగా, a × b = b × a
3 × [latex]\frac {1}{5}[/latex] = [latex]\frac {1}{5}[/latex] × 3 = [latex]\frac {3}{5}[/latex]
నీ ప్రగతిని సరిచూసుకో [పేజి నెం. 68]
కింది వాటిని కనుగొనండి.
i) 5 × 3[latex]\frac {2}{7}[/latex]
సాధన.
5 × 3[latex]\frac {2}{7}[/latex] = [latex]\frac{5}{1} \times \frac{23}{7}[/latex]
= [latex]\frac{5 \times 23}{1 \times 7}[/latex]
= [latex]\frac {115}{7}[/latex]
= 16[latex]\frac {3}{7}[/latex]
(లేదా)
5 × 3[latex]\frac {2}{7}[/latex] = 5 × [latex]\left(3+\frac{2}{7}\right)[/latex]
= 5 × 3 + [latex]\frac{5 \times 2}{7}[/latex]
= 15 + [latex]\frac {10}{7}[/latex]
= 15 + 1 + [latex]\frac {3}{7}[/latex]
= 16[latex]\frac {3}{7}[/latex]
ii) 2[latex]\frac {5}{9}[/latex] × 3
సాధన.
2[latex]\frac {5}{9}[/latex] × 3
= [latex]\frac{23}{9} \times \frac{3}{1}[/latex]
= [latex]\frac{23 \times 3}{3 \times 3}[/latex]
= [latex]\frac {23}{3}[/latex]
= 7
(లేదా)
2[latex]\frac {5}{9}[/latex] × 3 = [latex]\left(2+\frac{5}{9}\right)[/latex] × 3
= 2 × 3 + [latex]\frac{5 \times 3}{9}[/latex]
= 6 + [latex]\frac {5}{3}[/latex] = 6 + 1 + [latex]\frac {2}{3}[/latex] = 7 [latex]\frac {2}{3}[/latex]
iii) 2[latex]\frac {4}{7}[/latex] × 3
సాధన.
2[latex]\frac {4}{7}[/latex] × 3
= [latex]\frac{18}{7} \times \frac{3}{1}[/latex]
= [latex]\frac{18 \times 3}{7}[/latex]
= [latex]\frac {54}{7}[/latex]
= 7[latex]\frac {5}{7}[/latex]
(లేదా)
2[latex]\frac {4}{7}[/latex] × 3 = [latex]\left(2+\frac{4}{7}\right)[/latex] × 3
= 2 × 3 + [latex]\frac{4 \times 3}{7}[/latex]
= 6 + [latex]\frac {12}{7}[/latex]
= 6 + 1 + [latex]\frac {5}{7}[/latex]
= 7 + [latex]\frac {5}{7}[/latex]
= 7[latex]\frac {5}{7}[/latex]
iv) 3 × 1[latex]\frac {3}{4}[/latex]
సాధన.
3 × 1[latex]\frac {3}{4}[/latex]
= [latex]\frac{3}{1} \times \frac{7}{4}[/latex]
= [latex]\frac{3 \times 7}{1 \times 4}[/latex]
= [latex]\frac {21}{4}[/latex]
= 5[latex]\frac {1}{4}[/latex]
(లేదా)
3 × [latex]\left(1+\frac{3}{4}\right)[/latex] = 3 × 1 + 3 × [latex]\frac {3}{4}[/latex]
= 3 + [latex]\frac {9}{4}[/latex]
= 3 + 2 + [latex]\frac {1}{4}[/latex]
= 5 + [latex]\frac {1}{4}[/latex]
= 5[latex]\frac {1}{4}[/latex]
![]()
ప్రయత్నించండి [పేజి నెం. 69]
కింది భిన్నాల లబ్దాలను పరిశీలించండి.
i) [latex]\frac{1}{5} \times \frac{2}{3}=\frac{2}{15}[/latex] (రెండు క్రమ భిన్నాల లబ్ధం)
ii) [latex]\frac{3}{2} \times \frac{5}{4}=\frac{15}{8}[/latex] (రెండు అపక్రమ భిన్నాల లబ్ధం)
iii) [latex]\frac{2}{3} \times \frac{5}{3}=\frac{10}{9}[/latex] (క్రమ అపక్రమ భిన్నాల లబ్దం)
పై లబ్దాలను పరిశీలించండి.
రెండు భిన్నాలను ఒకదానికొకటి గుణించినపుడు ఏర్పడే లబ్దం, ఆయా ప్రతీ భిన్నం కంటే తక్కువా ? ఎక్కువా? మీ సమాధానాన్ని సమర్థించండి.
సాధన.
i) [latex]\frac{1}{5} \times \frac{2}{3}=\frac{2}{15}[/latex] (రెండు క్రమ భిన్నాల లబ్ధం)
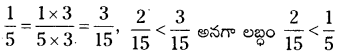
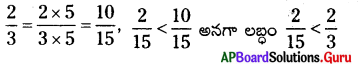
రెండు క్రమభిన్నాలను గుణించగా వచ్చు లబ్ధము, ఆ రెండు భిన్నాలలో ప్రతి భిన్నం కన్నా తక్కువ.
ii) [latex]\frac{3}{2} \times \frac{5}{4}=\frac{15}{8}[/latex] (రెండు అపక్రమ భిన్నాల లబ్ధం)
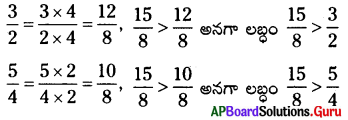
రెండు అపక్రమ భిన్నాలను గుణించగా, వచ్చు లబ్ధము ఆ రెండు భిన్నాలలో ప్రతిభిన్నం కన్నా ఎక్కువ.
iii) [latex]\frac{2}{3} \times \frac{5}{3}=\frac{10}{9}[/latex] (క్రమ అపక్రమ భిన్నాల లబ్దం)
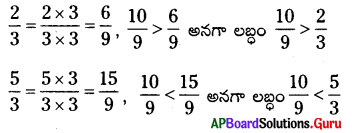
క్రమ, అపక్రమ భిన్నాలను గుణించగా వచ్చు లబ్దము క్రమ భిన్నం కన్నా పెద్దది లేదా సమానంగాను, అపక్రమ భిన్నం కన్నా చిన్నదిగాను ఉంటుంది.
[పేజి నెం. 71]
కింది వాటిని కనుగొనండి.
అ) 4 ÷ [latex]\frac {1}{8}[/latex]
ఆ) 9 ÷ [latex]\frac {3}{4}[/latex]
ఇ) 7 ÷ [latex]\frac {2}{3}[/latex]
ఈ) 35 ÷ [latex]\frac {7}{3}[/latex]
ఉ) 4 ÷ [latex]\frac {15}{8}[/latex]
సాధన.
అ) 4 ÷ [latex]\frac {1}{8}[/latex]
= 4 × [latex]\frac {8}{1}[/latex]
= [latex]\frac{4 \times 8}{1}[/latex]
= [latex]\frac {32}{1}[/latex]
= 32
ఆ) 9 ÷ [latex]\frac {3}{4}[/latex]
= 9 × [latex]\frac {4}{3}[/latex]
= [latex]\frac{9 \times 4}{3}[/latex]
= [latex]\frac {36}{3}[/latex]
= 12
ఇ) 7 ÷ [latex]\frac {2}{3}[/latex]
= 7 × [latex]\frac {3}{2}[/latex]
= [latex]\frac{7 \times 3}{2}[/latex]
= [latex]\frac {21}{2}[/latex]
= 10[latex]\frac {1}{2}[/latex]
ఈ) 35 ÷ [latex]\frac {7}{3}[/latex]
= 35 × [latex]\frac {3}{7}[/latex]
= [latex]\frac{35 \times 3}{7}[/latex]
= [latex]\frac {105}{7}[/latex]
= 15
ఉ) 4 ÷ [latex]\frac {15}{8}[/latex]
= 4 × [latex]\frac {8}{15}[/latex]
= [latex]\frac{4 \times 8}{15}[/latex]
= [latex]\frac {32}{15}[/latex]
= 2[latex]\frac {2}{15}[/latex]
![]()
[పేజి నెం. 72]
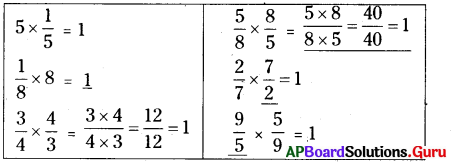
కింది లబ్దాలను పరిశీలించి, ఖాళీలు పూరించండి.

సాధన.
నీ ప్రగతిని సరిచూసుకో [పేజి నెం. 73]
కింది పట్టికలో గల భిన్నాలకు వ్యుత్ప్రమాలను రాయండి.
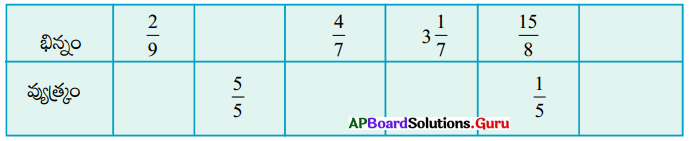
సాధన.
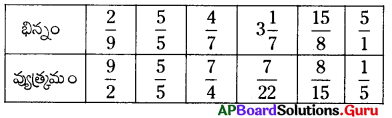
(భిన్నం [latex]\frac{a}{b}[/latex] యొక్క వృత్రమం [latex]\frac{b}{a}[/latex]).
[పేజి నెం. 74]
i) [latex]\frac {7}{9}[/latex] ÷ 4 ii) [latex]\frac {3}{4}[/latex] ÷ 9 iii) 4[latex]\frac {1}{2}[/latex] ÷ 6 iv) 2[latex]\frac {1}{5}[/latex] ÷ 3ల విలువలు కనుగొనండి
సాధన.
i) [latex]\frac {7}{9}[/latex] ÷ 4
= [latex]\frac{7}{9} \div \frac{4}{1}[/latex]
= [latex]\frac{7}{9} \times \frac{1}{4}[/latex]
= [latex]\frac{7 \times 1}{9 \times 4}[/latex]
= [latex]\frac {7}{36}[/latex]
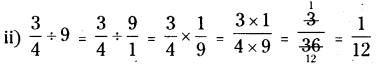
iii) 4[latex]\frac {1}{2}[/latex] ÷ 6
= [latex]\frac{9}{2} \div \frac{6}{1}[/latex]
= [latex]\frac{9}{2} \times \frac{1}{6}[/latex]
= [latex]\frac{9 \times 1}{2 \times 6}[/latex]
= [latex]\frac {9}{12}[/latex]
= [latex]\frac {3}{4}[/latex]
iv) 2[latex]\frac {1}{5}[/latex] ÷ 3
= [latex]\frac{11}{5} \div \frac{3}{1}[/latex]
= [latex]\frac{11}{5} \times \frac{1}{3}[/latex]
= [latex]\frac{11 \times 1}{5 \times 3}[/latex]
= [latex]\frac {11}{15}[/latex]
![]()
నీ ప్రగతిని సరిచూసుకో [పేజి నెం. 78]
ఖాళీలను పూరించండి.
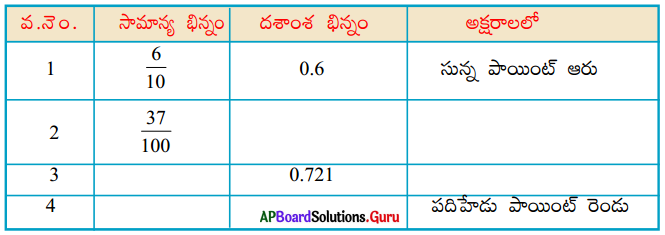
సాధన.
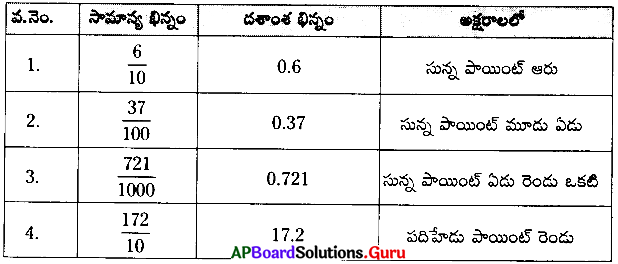
నీ ప్రగతిని సరిచూసుకో [పేజి నెం. 79]
1. కింది దశాంశ బిందువులలో వృత్తం చుట్టబడిన అంకె యొక్క స్థానవిలువలు రాయండి.
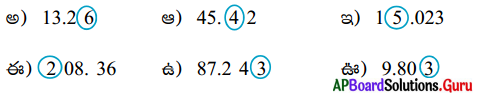
సాధన.
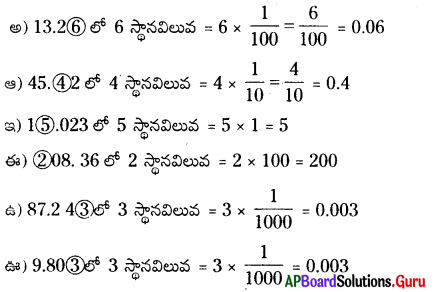
2. కింది వాటిని దశాంశ రూపంలో రాయండి.

సాధన.
అ) 700 + 40 + 2 + 0.1 + 0.03 + 0.006 = 742.136
ఆ) 9000 + 800 + 3 + 0.2 + 0.05 + 0.007 = 983.257
ఇ) 6000 + 400 + 20 + 1 + 0.2 + 0.05 + 0.009 = 6421. 259
ఈ) 400 + 5 + 0.1 + 0.08 = 405.18
3. కింది వాటిని దశాంశ మరియు భిన్న రూపంలో విస్తరించండి.
అ) 164.238
ఆ) 968.054
సాధన.

![]()
నీ ప్రగతిని సరిచూసుకో [పేజి నెం. 80]
1. భిన్నాలను దశాంశాలుగా మార్చండి.

సాధన.
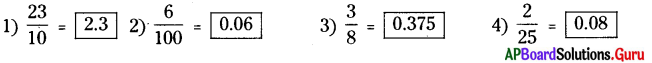
2. కింది దశాంశాలను సామాన్య భిన్నాలుగా మార్చండి.
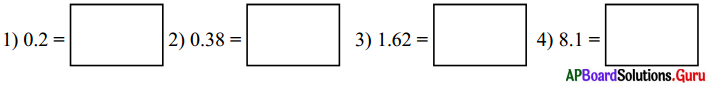
సాధన.
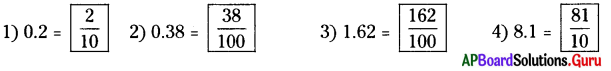
ఉదాహరణలు
1. [latex]\frac {11}{5}[/latex]ను మిశ్రమ భిన్నంగా వ్యక్తపరచండి.
సాధన.

[latex]\frac {11}{5}[/latex] యొక్క మిశ్రమ భిన్నం 2[latex]\frac {11}{5}[/latex].
దీనిని సంఖ్యారేఖ పై కింది విధంగా చూపవచ్చు.
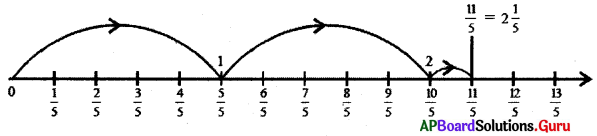
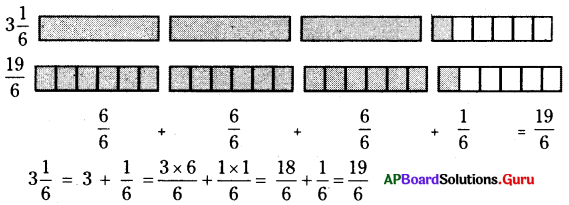
2. 3[latex]\frac {1}{6}[/latex] ను అపక్రమ భిన్నంగా మార్చండి.
సాధన.
పట రూపంలో కింది విధంగా చూడగా
3. [latex]\frac {2}{7}[/latex] సమాన భిన్నాలను రాయండి.
సాదన.
[latex]\frac {2}{7}[/latex] యొక్క సమాన భిన్నాలు
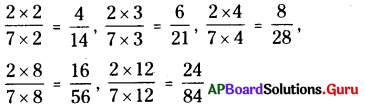
4. సూక్ష్మీకరించండి.
అ) [latex]1 \frac{4}{5}+2 \frac{5}{6}[/latex]
ఆ) [latex]5 \frac{1}{4}-2 \frac{5}{6}[/latex]
సాధన.


![]()
5. సతీష్ 1[latex]\frac {2}{5}[/latex] మీ. రిబ్బన్ మరియు పద్మ 2[latex]\frac {3}{4}[/latex] మీ. రిబ్బన్ కొంటే ఇద్దరూ కొన్న రిబ్బన్ మొత్తం పొడవెంత ?
సాధన.
సతీష్ మరియు పద్మ కొన్న మొత్తం రిబ్బన్ పొడవు = 1[latex]\frac {2}{5}[/latex] + 2[latex]\frac {3}{4}[/latex] మీ.

6. 2[latex]\frac {4}{5}[/latex] భిన్నానికి ఎంత కలిపిన 5[latex]\frac {2}{3}[/latex] వస్తుంది ?
సాధన.
2[latex]\frac {4}{5}[/latex] కు ఎంత కలిపిన 5[latex]\frac {2}{3}[/latex], వచ్చుననగా 5[latex]\frac {2}{3}[/latex] నుండి 2[latex]\frac {4}{5}[/latex] తీసివేయాలి.

7. i) [latex]\frac{3}{4} \times \frac{1}{7}[/latex] ii) [latex]\frac{5}{3} \times \frac{7}{2}[/latex] iii) [latex]\frac{8}{3} \times \frac{4}{7}[/latex] iv) [latex]2 \frac{1}{5} \times \frac{1}{3}[/latex] గుణించండి.
సాధన.

8. (i) [latex]\frac {2}{9}[/latex] ను [latex]\frac {4}{5}[/latex] చే (ii) [latex]\frac {3}{5}[/latex] ను 14 చే (iii) 3[latex]\frac {1}{2}[/latex] ను [latex]\frac {1}{7}[/latex] చే (iv) 4[latex]\frac {3}{7}[/latex] ను 1[latex]\frac {2}{7}[/latex] చే గుణించండి.
సాధన.
(i) [latex]\frac {2}{9}[/latex] × [latex]\frac {4}{5}[/latex]
= [latex]\frac{2 \times 4}{9 \times 5}[/latex]
= [latex]\frac {8}{45}[/latex]
(ii) [latex]\frac {3}{5}[/latex] × 14
= [latex]\frac{3 \times 14}{5}[/latex]
= [latex]\frac {42}{5}[/latex]
(iii) 3[latex]\frac {1}{2}[/latex] × [latex]\frac {1}{7}[/latex]
= [latex]\frac{7}{2} \times \frac{1}{7}[/latex]
= [latex]\frac {1}{2}[/latex]
(iv) 4[latex]\frac {3}{7}[/latex] × 1[latex]\frac {2}{7}[/latex]
= [latex]\frac{31}{7} \times \frac{9}{7}[/latex]
= [latex]\frac{279}{49}[/latex]
![]()
9. ఒక తరగతిలో గల 40 మంది విద్యార్థులలో [latex]\frac {2}{5}[/latex] వ భాగం బాలురు. అయిన ఆ తరగతిలో బాలురెందరు? సాధన.
తరగతిలో మొత్తం విద్యార్థులు = 40
∴ బాలుర సంఖ్య = మొత్తం విద్యార్థులలో [latex]\frac {2}{5}[/latex] వ భాగం.
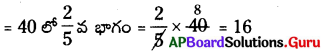
10. దీర్ఘచతురస్రాకార పార్కు పొడవు 7[latex]\frac {2}{3}[/latex] మీ., వెడల్పు 3[latex]\frac {1}{5}[/latex] అయిన పార్కువైశాల్యమెంత?
సాధన.
పార్కు పొడవు = 7[latex]\frac {2}{3}[/latex] మీ. = [latex]\frac {23}{3}[/latex] మీ.
వెడల్పు = 3[latex]\frac {1}{5}[/latex]మీ. = [latex]\frac {16}{5}[/latex] మీ.
∴ పార్కు వైశాల్యం = పొడవు × వెడల్పు
= [latex]\frac {23}{3}[/latex] × [latex]\frac {16}{5}[/latex] మీ.2
= [latex]\frac {368}{15}[/latex] మీ.2
= 24[latex]\frac {8}{15}[/latex] మీ.2
11. 3.6, 2.35, 0.472 లను సజాతి భిన్నాలుగా మార్చండి.
సాధన.
3.6, 2.35, 0.472 లలో గరిష్ఠ దశాంశ స్థానాల సంఖ్య 3 అందులో ప్రతీ వాటిని 3 సమానంగా దశాంశ స్థానాలుగా మార్చాలి.
3.6 = 3.600
2.35 = 2.350
0.472
3.6, 2.35, 0.472 లు 3.600, 2.350, 0.472 సజాతి దశాంశాలుగా మారుతాయి.
12. 5.623 మరియు 5.64 ను పోల్చండి.
సాధన.

దశాంశ భిన్నాలలో పూర్ణాంక భాగం, దశాంశ భాగం ఒకే విధంగా ఉంది. శతక భాగంలో భేదం కలదు.
2 శతక భాగాలు కన్నా < 4 శతకాలు ఎక్కువ 5.623 < 5.64.
![]()
13. 24.117, 24.118, 29.421 లను అవరోహణ క్రమంలో రాయండి.
సాధన.
పూర్ణాంక భాగాలను పోల్చగా 29.421 పెద్దదని తెలుస్తాయి.
మిగిలినవి, 24.117 మరియు 24. 118 లను పోల్చగా వీటిలో పూర్ణాంక భాగం, దశాంశ, శతక భాగాలు ఒకేలా ఉన్నవి. మనం సహస్రాంశ భాగం పోల్చాలి.
7 శతకాలు < 8 శతకాలు, కావున, 24.118> 24.117
అవరోహణ క్రమం , 29.421, 24.118, 24.117.
14. 53.08, 5.936, 188.5 లను కలపండి.
సాధన.
ఇచ్చిన దశాంశాలను 3 దశాంశ స్థానాలు మార్చే విధంగా సజాతి దశాంశ భిన్నాలుగా మార్చి తర్వాత కలపండి.
53.08 = 53.080, 5.936, 188.5 = 188.500

15. శేఖర్ 6 కి.మీ. 40 మీ.లను బస్సులో, 3 కి.మీ. 320 మీ. లను కారులో మిగిలిన దూరం 1 కి.మీ. 30 మీ. నడిచి వెళ్లాడు. అయిన అతడు ప్రయాణించిన మొత్తం దూరం ఎంత?
సాధన.
శేఖర్ బస్సులో ప్రయాణించిన దూరం = 6 కి.మీ. 40 మీ. = 6.040 కి.మీ.
శేఖర్ కారులో ప్రయాణించిన దూరం = 3 కి.మీ. 320 మీ. = 3.320 కి.మీ.
శేఖర్ నడిచి ప్రయాణించిన దూరం = 1 కి.మీ. 30 మీ. = 1.030 కి.మీ.
శేఖర్ మొత్తం ప్రయాణించిన దూరం = 6.040 + 3.320 + 1.030 = 10.390
శేఖర్ ప్రయాణించిన మొత్తం దూరం = 10.390 కి.మీ.
![]()
16. కావ్య 10 కి.గ్రా. బరువైన కూరగాయలను కొన్నది. వీటిలో 3 కిలోల 500 గ్రా. ఉల్లిపాయలు, 2 కిలోల 75 గ్రా. టమోటాలు మరియు మిగిలినవి బంగాళదుంపలు. అయిన బంగాళదుంపల బరువెంత?
సాధన.
ఉల్లిపాయల బరువు = 3 కిలోల 500 గ్రా. = 3.500 కి.గ్రా.
టమోటాల బరువు = 2 కిలోల 75 గ్రా. = 2.075 కి.గ్రా.
ఉల్లి మరియు టమోటా బరువు = 3.500 + 2.075 = 5.575
మొత్తం కూరగాయల బరువు = 10 కి.గ్రా.
బంగాళదుంపల బరువు = 10.000 కి.గ్రా. – 5.575 కి.గ్రా.
= 4.425 కి.గ్రా.