AP Board 6th Class Maths Solutions Chapter 10 ప్రాయోజిక జ్యామితి Unit Exercise

AP SCERT 6th Class Maths Textbook Solutions Chapter 10 ప్రాయోజిక జ్యామితి Unit Exercise Questions and Answers.

AP State Syllabus 6th Class Maths Solutions 10th Lesson ప్రాయోజిక జ్యామితి Unit Exercise

ప్రశ్న 1.
X కేంద్రంగా 10 సెం.మీ. వ్యాసం గల ఒక వృత్తం నిర్మించుము.
సాధన.
వ్యాసం = 10 సెం.మీ. కావున వ్యాసార్ధం = 5 సెం.మీ. లతో వృత్తాన్ని గీయాలి.

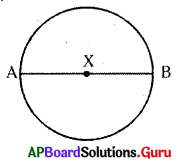
వ్యా సం AB = 10 సెం.మీ.
వ్యాసార్ధం XB = 5 సెం.మీ.

ప్రశ్న 2.
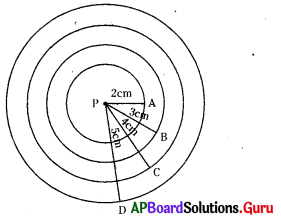
P కేంద్రంగా 2సెం.మీ., 3 సెం.మీ., 4 సెం.మీ. మరియు 5 సెం.మీ., వ్యాసార్ధాలు గల నాలుగు వృత్తాలు గీయుము.
సాధన.
P – వృత్త కేంద్రము. (పై వృత్తాలను ఏకకేంద్ర వృత్తాలు అంటారు.)

3. కోణమానిని ఉపయోగించి కింది కోణాలు నిర్మించండి.

ప్రశ్న (అ)
75°
సాధన.

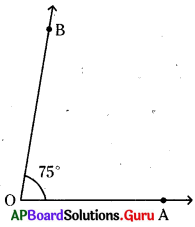
నిర్మాణక్రమము :

1. కొంత పొడవు గల [latex]\overrightarrow{\mathrm{OA}}[/latex] కిరణం గీయవలెను.
2. కోణమానిని మధ్యబిందువును ‘O’ వద్ద ఉంచి [latex]\overrightarrow{\mathrm{OA}}[/latex] ఆధారరేఖతో ఏకీభవించేటట్లు చేయాలి.
3. 75° వద్ద B బిందువును గుర్తించాలి.
4. OBలు కలపాలి. [latex]\angle \mathrm{AOB}[/latex] = 75°

ప్రశ్న (ఆ)
15°
సాధన.
[latex]\angle \mathrm{PQR}[/latex] = 15°

నిర్మాణ క్రమము :

1. కొంత పొడవు గల [latex]\overrightarrow{\mathrm{QP}}[/latex] కిరణం గీయవలెను.
2. కోణమానిని మధ్య బిందువును ‘Q’ వద్ద ఉంచి [latex]\overrightarrow{\mathrm{QP}}[/latex] ఆధారరేఖతో ఏకీభవించేటట్లు చేయాలి.
3. 15° వద్ద R బిందువును గుర్తించాలి.
4. QR లు కలపాలి. [latex]\angle \mathrm{PQR}[/latex] = 15.

ప్రశ్న (ఇ)
105°
సాధన.

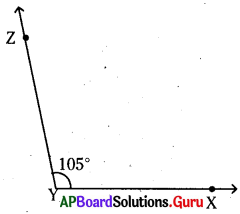
నిర్మాణక్రమము :

1. కొంత పొడవు గల [latex]\overrightarrow{\mathrm{YX}}[/latex] కిరణం గీయవలెను.
2. కోణమానిని మధ్యబిందువును ‘Y’ వద్ద ఉంచి [latex]\overrightarrow{\mathrm{YX}}[/latex] ఆధారలేఖతో ఏకీభవించేటట్లు చేయాలి.
3. 105° వద్ద Z బిందువును గుర్తించాలి.
4. YZ లు కలపాలి. [latex]\angle \mathrm{XYZ}[/latex] = 105° కోణం.

ప్రశ్న 4.
[latex]\angle \mathrm{ABC}[/latex] = 50° నిర్మించి, దానికి సమానమగు [latex]\angle \mathrm{XYZ}[/latex] ను కోణమానిని సాయం లేకుండా నిర్మించండి.
సాధన.

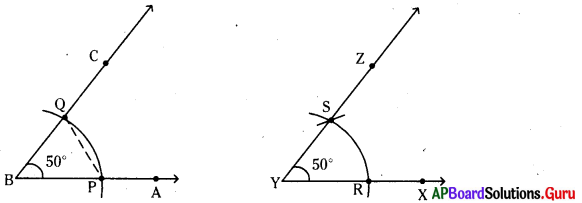
[latex]\angle \mathrm{ABC}[/latex] = 50° మరియు [latex]\angle \mathrm{XYZ}[/latex] = 50°.

నిర్మాణక్రమం :
1. కోణమానిని ఉపయోగించి [latex]\angle \mathrm{ABC}[/latex] = 50° కోణాన్ని గీయాలి.
2. B కేంద్రంగా కొంత వ్యాసార్ధంతో [latex]\overrightarrow{\mathrm{BA}}[/latex] మరియు [latex]\overrightarrow{\mathrm{BC}}[/latex] కిరణాలపై ఒక చాప రేఖను గీచి, ఖండన బిందువులను P, Q లుగా గుర్తించాలి.
3. [latex]\overrightarrow{\mathrm{YX}}[/latex] కిరణంపై Y కేంద్రంగా పై తీసుకొన్న వ్యాసార్ధంతో ఒక చాపరేఖను గీయాలి. ఇది [latex]\overrightarrow{\mathrm{YX}}[/latex] ని R వద్ద ఖండించినది. ఇపుడు R కేంద్రంగా [latex]\overrightarrow{\mathrm{PQ}}[/latex] వ్యాసార్ధంతో ఇంతకు ముందు గీచిన చాపరేఖను ఖండించాలి. ఖండన బిందువును S గా గుర్తించాలి. Y, S గుండా [latex]\overrightarrow{\mathrm{YZ}}[/latex] కిరణాన్ని గీయాలి. మనకు కావలసిన [latex]\angle \mathrm{XYZ}[/latex] = 50° కోణం ఏర్పడినది.

ప్రశ్న 5.
[latex]\angle \mathrm{DEF}[/latex] = 60° నిర్మించి, దానిని సమద్విఖండన చేయుము. ప్రతి సగాన్ని కోణమానితో కొలవండి.
సాధన.
[latex]\angle \mathrm{DEF}[/latex] = 60°

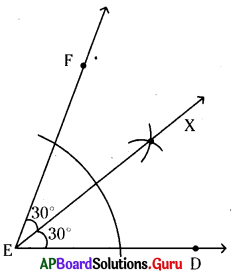
[latex]\angle \mathrm{DEF}[/latex] యొక్క కోణ సమద్విఖండన కిరణం [latex]\overrightarrow{\mathrm{OX}}[/latex].
[latex]\angle \mathrm{DEF}[/latex] = [latex]\angle \mathrm{XEF}[/latex] = [latex]\frac {[latex]\angle \mathrm{DEF}[/latex]}{2}[/latex] = [latex]\frac {60°}{2}[/latex] = 30°