AP Board 10th Class Maths Solutions Chapter 7 నిరూపక రేఖాగణితం Optional Exercise

SCERT AP 10th Class Maths Textbook Solutions Chapter 7 నిరూపక రేఖాగణితం Optional Exercise Textbook Exercise Questions and Answers.

AP State Syllabus 10th Class Maths Solutions 7th Lesson నిరూపక రేఖాగణితం Optional Exercise

ప్రశ్న 1.
వృత్తం ‘Q’ యొక్క కేంద్రం -అక్షంపై ఉన్నది. మరియు 2. (0, 7) మరియు (0, -1) లు ఆ వృత్తం పై బిందువులు. వృత్తం ‘Q’ ధన X-అక్షాన్ని బిందువు (P, 0) వద్ద ఖండించిన ‘P’ విలువ ఎంత ?
సాధన.

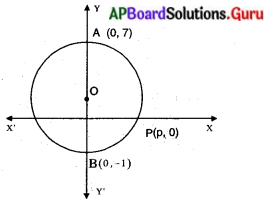
పై పటం నుండి వృత్తంపై బిందువులు A (0, 7), B (0, – 1) అనుకుంటే A, B లు వ్యాసాగ్రాలు.
వృత్తకేంద్రం ‘O’ = A, B ల మధ్య బిందువు = [latex]\left(\frac{x_{1}+x_{2}}{2}, \frac{y_{1}+y_{2}}{2}\right)[/latex]
= [latex]\left(\frac{0+0}{2}, \frac{7-1}{2}\right)[/latex] = (0, 3)
∴ వృత్తకేంద్రం = (0, 3)
వృత్త వ్యాసార్ధం r = OA = |7 – 3| = 4 యూనిట్లు
వృత్తం Q ధన X – అక్షాన్ని (P, 0) వద్ద ఖండించును.
O(0, 3), P(P, 0)
∴ OP = r = 4
[latex]\sqrt{\mathrm{P}^{2}+3^{2}}[/latex] = 4
[latex]\sqrt{\mathrm{P}^{2}+9}[/latex] = 4
⇒ P² + 9 = 16
⇒ P² = 16 – 9 = 7
⇒ P = √7,

2వ పద్ధతి :
పై పటం నుండి వృత్త కేంద్రం O = A, B ల మధ్య బిందువు = [latex]\left(\frac{0+0}{2}, \frac{7-1}{2}\right)[/latex] = (0, 3)
A (0, 7), (P, 0) బిందువులు వృత్తం పై కలవు.
∴ OA = OP
[latex]\sqrt{(0-0)^{2}+(7-3)^{2}}=\sqrt{(P-0)^{2}+(0-3)^{2}}[/latex]
[latex]\sqrt{4^{2}}=\sqrt{\mathrm{P}^{2}+9}[/latex]
⇒ 4² = P² + 9
16 – 9 = P²
7 = P²
√7 = P.

ప్రశ్న 2.
బిందువులు A(2, 3), B(- 2, – 3) మరియు C(4, 3) శీర్చాలతో త్రిభుజం ∆ABC ఏర్పడినది. భుజం BC మరియు. శీర్షం A యొక్క కోణ సమద్విఖండన రేఖల ఖండన బిందువును కనుగొనండి.
సాధన.

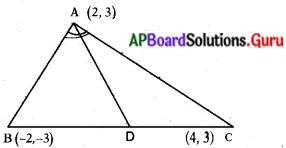
A (2, 3), B (- 2, – 3), C (4, 3) లు శీర్షాలుగా గల త్రిభుజం ∆ ABC
BC ని A యొక్క కోణ సమద్విఖండన రేఖ D వద్ద ఖండిస్తున్నది అనుకొనుము.
అప్పుడు [latex][/latex] ……….. (1) (∵ కోణ సమద్విఖండన సిద్ధాంతము)
AB = [latex]\sqrt{(-2-2)^{2}+(-3-3)^{2}}[/latex]
= [latex]\sqrt{16+36}=\sqrt{52}[/latex]
= 2√13

AC = [latex]\sqrt{(4-2)^{2}+(3-3)^{2}}[/latex]
= [latex]\sqrt{2^{2}+0^{2}}[/latex] = 2

∴ [latex]\frac{\mathrm{BD}}{\mathrm{DC}}=\frac{2 \sqrt{13}}{2}[/latex] = √13 : 1
(∵ AB, AC లను (1) లో రాయగా)
అనగా BCని D అంతరంగా√13 : 1 నిష్పత్తిలో ఖండిస్తుంది.
∴ D = [latex]\left(\frac{m_{1} x_{2}+m_{2} x_{1}}{m_{1}+m_{2}}, \frac{m_{1} y_{2}+m_{2} y_{1}}{m_{1}+m_{2}}\right)[/latex]

D = [latex]\left(\frac{\sqrt{13} \times 4+1(-2)}{\sqrt{13}+1}, \frac{\sqrt{13} \times 3+1(-3)}{\sqrt{13}+1}\right)[/latex]

D = [latex]\left[\frac{4 \sqrt{13}-2}{\sqrt{13}+1}, \frac{3 \sqrt{13}-3}{\sqrt{13}+1}\right][/latex]
BC ని A యొక్క కోణ సమద్విఖండన రేఖ ఖండించే బిందువు D = [latex]\left[\frac{4 \sqrt{13}-2}{\sqrt{13}+1}, \frac{3 \sqrt{13}-3}{\sqrt{13}+1}\right][/latex].

సరిచూచుట :
B, D, C లు సరేఖీయాలు అవుతాయని చూపి సరిచూసుకోవచ్చును.

ప్రశ్న 3.
సమబాహు త్రిభుజం ∆ABC యొక్క భుజం BC X – అక్షానికి సమాంతరంగా ఉంది. దాని భుజాలు BC, CA, AB ల గుండా పోయే సరళరేఖల వాలులు కనుగొనుము.
సాధన.

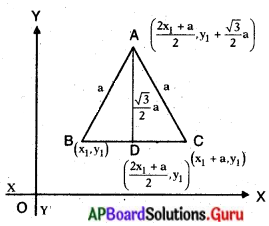
∆ABC సమబాహు త్రిభుజం AB = BC = AC = a యూనిట్లు మరియు B(x₁, y₁) అనుకొందాం.
BC మధ్య బిందువు D మరియు AD; ∆ABC యొక్క ఎత్తు = [latex]\frac{\sqrt{3}}{2}[/latex]a యూనిట్లు అవుతుంది.
D = AC ల మధ్యబిందువు = [latex]\left(\frac{x_{1}+x_{1}+a}{2}, \frac{y_{1}+y_{1}}{2}\right)=\left(\frac{2 x_{1}+a}{2}, y_{1}\right)[/latex] మరియు C = (x₁ + a,y₁),
A [latex]\left(\frac{2 x_{1}+a}{2}, y_{1}+\frac{\sqrt{3}}{2} a\right)[/latex]
ఇప్పుడు, AB పాలు = [latex]\frac{y_{2}-y_{1}}{x_{2}-x_{1}}[/latex]

∴ AB వాలు = √3
BC వాలు = [latex]\frac{y_{1}-y_{1}}{x_{1}+a-x_{1}}=\frac{0}{a}[/latex] = 0
లేదా BC, X – అక్షానికి సమాంతరం. కావున BC వాలు = 0
AC వాలు = [latex]\frac{y_{1}-\left(y_{1}+\frac{\sqrt{3}}{2} a\right)}{x_{1}+a-\left(\frac{2 x_{1}+a}{2}\right)}[/latex]

= [latex]\frac{y_{1}-y_{1}-\frac{\sqrt{3}}{2} a}{x_{1}+a-x_{1}-\frac{a}{2}}[/latex]

= [latex]\frac{-\frac{\sqrt{3}}{2} a}{\frac{a}{2}}=-\frac{\sqrt{3}}{2} a \times \frac{2}{a}[/latex] = – √3

AC వాలు = – √3.

2వ పద్ధతి :

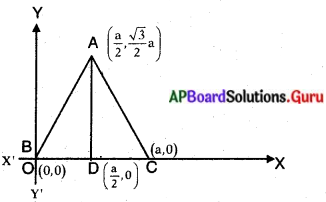
∆ABC సమబాహు త్రిభుజం AB = BC = AC = a యూనిట్లు
X – అక్షంపై BC భుజం కలదు అనుకుందాం. (ప్రతిరేఖ దానికదే సమాంతరము కాబట్టి BC X – అక్షం)
B (0, 0) అయిన C(a, 0) అవుతుంది. BC ల మధ్యబిందువు
D = [latex]\left(\frac{0+a}{2}, \frac{0+0}{2}\right)[/latex] = ([latex]\frac{a}{2}[/latex], 0)
AD = [latex]\frac{\sqrt{3}}{2}[/latex] a
[సమబాహు త్రిభుజ ఉన్నతి = [latex]\frac{\sqrt{3}}{2}[/latex] × భుజం]
∴ A = ([latex]\frac{a}{2}[/latex], [latex]\frac{\sqrt{3}}{2}[/latex] a)
∴ త్రిభుజ శీర్షాలు A([latex]\frac{a}{2}[/latex], [latex]\frac{\sqrt{3}}{2}[/latex] a), B(0, 0), C(a, 0)

∴ AB రేఖ వాలు = [latex]\frac{y_{2}-y_{1}}{x_{2}-x_{1}}=\frac{0-\frac{\sqrt{3}}{2} a}{0-\frac{a}{2}}[/latex]
= [latex]-\frac{\sqrt{3}}{2} a \times-\frac{2}{a}=\sqrt{3}[/latex]

BC-రేఖ వాలు = [latex]\frac{0-0}{a-0}=\frac{0}{a}=0[/latex]

AC రేఖ వాలు = [latex]\frac{0-\frac{\sqrt{3}}{2} a}{0-\frac{a}{2}}=\frac{-\frac{\sqrt{3}}{2} a}{\frac{a}{2}}[/latex]
= [latex]\frac{-\sqrt{3}}{2} a \times \frac{2}{a}=-\sqrt{3}[/latex].

3వ పద్ధతి :

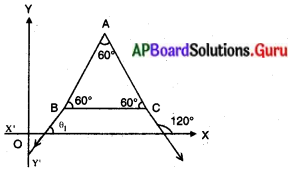
∆ABC సమబాహు త్రిభుజము మరియు BC, X – అక్షానికి సమాంతరము. [latex]\overleftrightarrow{A B}[/latex] రేఖ X – అక్షం ధనదిశలో చేసే కోణము θ₁, అనుకొనుము.
θ₁, = ∠ABC = 60° (∵ BC // X – అక్షం, θ₁, మరియు ∠ABC లు సదృశ్యకోణాలు)
[latex]\overleftrightarrow{A C}[/latex] X – అక్షం ధనదిశలో చేసే కోణం θ₂, అనుకొనుము. ర
θ₂ = ∠ACD = 120° [∵ BC // X – అక్షం, మరియు θ₂, ∠ACD లు సదృశ్యకోణాలు] కాని వాలు నిర్వచనం ఒక రేఖ X – అక్షం యొక్క ధనదిశలో చేసే కోణం θ అయితే ఆ రేఖవాలు ,
m = tan θ.
∴ A, B రేఖవాలు = tan θ₁ = tan 60° = √3
A, C రేఖవాలు = tan θ₂ = tan 120° .
= tan (90 + 30)
= – cot 30° = – √3 B
BC రేఖవాలు = tan 0° = 0 [∵ BC // X -అక్షం కాబట్టి X -అక్షంతో BC చేసే కోణం 0°].

ప్రశ్న 4.
a > b అయ్యేటట్లు భుజాలు ‘a’, ‘b’లు కలిగిన ఒక లంబకోణ త్రిభుజం ∆ABC ఉంది. దానిలో లంబకోణం యొక్క సమద్విఖండన రేఖ ద్వారా ఏర్పడిన రెండు చిన్న త్రిభుజాల లంబకేంద్రాల మధ్య దూరాన్ని కనుగొనుము.
సాధన.
పటంలో చూపినట్లు ∆ABC ఒక లంబకోణ త్రిభుజం
AC – కర్ణం ; ∠B = 90° అనుకుందాం
[latex]\overline{\mathrm{BG}}[/latex] కోణ సమద్విఖండన రేఖ వలన ఏర్పడే చిన్న త్రిభుజాలు వరుసగా ∆ABG, ∆BCG అనుకుందాం.
A, B, C శీర్షాల నిరూపకాలు వరుసగా A(0, a), B(0,0), C(b, 0) అనుకుందాం .

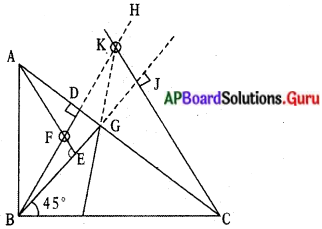
∴ [latex]\overline{\mathrm{BG}}[/latex] వాలు = m = tan 45° = 1 (∵ BG, ∠B యొక్క కోణ సమద్విఖండన రేఖ)
మరియు [latex]\overline{\mathrm{AC}}[/latex] వాలు = 0 = [latex]\frac{0-a}{b-0}=\frac{-a}{b}[/latex],
అదే విధంగా [latex]\overline{\mathrm{BC}}[/latex] అనునది X – అక్షంపై గలదు కావున [latex]\overline{\mathrm{BC}}[/latex] వాలు = 0

(I) [latex]\overline{\mathrm{BD}}[/latex] అనునది [latex]\overline{\mathrm{AC}}[/latex] పైకి గీయబడిన ‘ఉన్నతి’ అనుకుందాం.
∴ [latex]\overline{\mathrm{BD}}[/latex] వాలు = [latex]\frac{b}{a}[/latex]
(∵ m₁, m₂ = – 1, m, = 6)
∴ [latex]\overline{\mathrm{BD}}[/latex] సమీకరణం = (y – 0) = [latex]\frac{b}{a}[/latex] (x – 0)
⇒ bx = ay లేదా bx – ay = 0 – (1) అదే విధంగా.

(II) [latex]\overline{\mathrm{AE}}[/latex] అనునది ∆ABG నందలి. [latex]\overline{\mathrm{BD}}[/latex] పైకి గీయబడిన ‘ఉన్నతి’ అనుకుందాం = [latex]\overline{\mathrm{AE}}[/latex] వాలు = – 1
(∵ m₁, m₂ = – 1) అయిన
ఉన్నతి [latex]\overline{\mathrm{AE}}[/latex] సమీకరణం = (y – a) = 1(x – 0)
⇒ x – y = – a లేదా x – y + a = 0 – (2)
ఇపుడు (1), (2) సమీకరణాల ఖండన బిందువు అనునది రెండు ఉన్నతుల ([latex]\overline{\mathrm{AE}}[/latex], [latex]\overline{\mathrm{BD}}[/latex]) ఖండన బిందువు అనగా AABG యొక్క లంబకేంద్రం అగును.
∴ by – ay = 0 ______ (1) ⇒ bx – ay = 0
x – y = – a _________ (2) ⇒ ax – dy = – a²

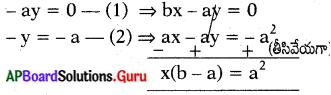
x = [latex]\frac{a^{2}}{b-a}[/latex] మరియు y = x + a .
⇒ y = [latex]\frac{a^{2}}{b-a}[/latex] + a
= [latex]\frac{a^{2}+a b-a^{2}}{b-a}=\frac{a b}{b-a}[/latex]
∴ ∆ABG యొక్క లంబ కేంద్రం ‘F’ యొక్క నిరూపకాలు = F|[latex]\left(\frac{a^{2}}{b-a}, \frac{a b}{b-a}\right)[/latex]
అదే విధంగా ∆BCG నందు,
[latex]\overline{\mathrm{GC}}[/latex] వాలు = [latex]\overline{\mathrm{AC}}[/latex] వాలు = – [latex]\frac{a}{b}[/latex]

‘B’ నుండి [latex]\overline{\mathrm{GC}}[/latex] మీదకు గీయబడు లంబం [latex]\overline{\mathrm{BD}}[/latex] గుండా పోవును.
(∵ ఒక రేఖకు ఒక బిందువు గుండా ఒకే ఒక లంబం గీయగలం)
∴ [latex]\overline{\mathrm{BH}}[/latex] అనునది [latex]\overline{\mathrm{CG}}[/latex] పైకి గల ఉన్నతి అనుకుందాం
[Note : a > b కావున ∆ABC నందు. ∠A ≠ ∠C ≠ 45 కావున ∆ABG, ∆BGC లలో ఒకటి తప్పనిసరిగా అధిక కోణ త్రిభుజం అగును)
[latex]\overline{\mathrm{BH}}[/latex] వాలు = [latex]\overline{\mathrm{BD}}[/latex] వాలు = [latex]\frac{b}{a}[/latex]

∴ [latex]\overline{\mathrm{BH}}[/latex] సమీకరణం = [latex]\overline{\mathrm{BH}}[/latex] సమీకరణం = bx – ay = 0 ((1) నుండి)
మరియు [latex]\overline{\mathrm{CJ}}[/latex] అనునది [latex]\overline{\mathrm{BG}}[/latex] పైకి లంబం
∴ [latex]\overline{\mathrm{CJ}}[/latex] వాలు = – 1 (∵ [latex]\overline{\mathrm{BG}}[/latex] వాలు = 1)
∴ [latex]\overline{\mathrm{CJ}}[/latex] సమీకరణం = (y – 0) = – 1(x – b)
⇒ x + y = b – (3)
∴ ABCG యొక్క ఉన్నతులు ([latex]\overline{\mathrm{CJ}}[/latex], [latex]\overline{\mathrm{BH}}[/latex]) ఖండన బిందువు,
దాని యొక్క లంబ కేంద్రం అగును.

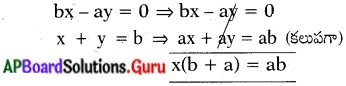
⇒ x = [latex]\frac{a b}{b+a}[/latex] అయిన y = – x + b = – [latex]\frac{a b}{b+a}[/latex] + b
= [latex]\frac{-\not ab+\not ab+b^{2}}{b+a}=\frac{b^{2}}{b+a}[/latex]
∴ K ([latex]\frac{a b}{b+a}[/latex], [latex]\frac{b^{2}}{b+a}[/latex] అనునది ∆BGC యొక్క లంబకేంద్రం నిరూపకాలు.
∴ రెండు లంబకేంద్రాల మధ్య దూరం [latex]\overline{\mathrm{KF}}[/latex] =

ప్రశ్న 5.
2x + 3y – 6 = 0 అను సరళరేఖ నిరూపకాక్షాలతో చేసే త్రిభుజం యొక్క గురుత్వ కేంద్రంను కనుగొనుము.
సాధన.

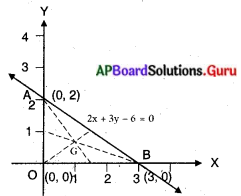
ఇచ్చిన సరళరేఖ 2x + 3y – 6 = 0
X – అక్షాన్ని ఖండించే బిందువు B వద్ద y నిరూపకం సున్న అనగా y = 0
y = 0 ⇒ 2x + 3(0) – 6 =.0
⇒ 2x – 6 = 0 ⇒ 2x = 6,
x = [latex]\frac{6}{2}[/latex] = 3
∴ B(3, 0) ఇదే విధంగా
x = 0 ⇒ 2(0) + 3y – 6 = 0
⇒ y = 2
∴ A(0, 2)
∴ 2x + 3y – 6 = 0 మరియు నిరూపకాక్షాలతో ఏర్పరిచే త్రిభుజ శీర్షాలు A(0, 2), 000, 0), B(3, 0)
∆ABC గురుత్వ కేంద్రం = [latex]\left(\frac{x_{1}+x_{2}+x_{3}}{3}, \frac{y_{1}+y_{2}+y_{3}}{3}\right)[/latex]
= [latex]\left(\frac{0+0+3}{3}, \frac{2+0+0}{3}\right)[/latex]
= [latex]\left(\frac{3}{3}, \frac{2}{3}\right)[/latex]
∆ABC గురుత్వకేంద్రం = (1, [latex]\frac{2}{3}[/latex])