AP Board 10th Class Maths Solutions Chapter 6 శ్రేఢులు Exercise 6.4

SCERT AP 10th Class Maths Textbook Solutions Chapter 6 శ్రేఢులు Exercise 6.4 Textbook Exercise Questions and Answers.

AP State Syllabus 10th Class Maths Solutions 6th Lesson శ్రేఢులు Exercise 6.4

ప్రశ్న 1.
ఈ క్రింది సంఘటనలలో ఏర్పడే సంఖ్యల జాబితాలలో ఏవి గుణశ్రేఢులను ఏర్పరుస్తాయి ?
(i) షర్మిల యొక్క మొదటి సం||ము జీతము 5,00,000/- ఆ తరువాత ప్రతి సం||ము ముందున్న సం||ము యొక్క జీతములో 10% పెరుగుతుంది.
సాధన.
షర్మిల మొదటి సం||ము జీతము = ₹ 5,00,000
2వ సం||ము జీతము = 5,00,000 [latex]\left(\frac{100+10}{100}\right)[/latex] = ₹ 5,50,000
3వ సం||ము జీతము = 5,50,000 [latex]\left(\frac{100+10}{100}\right)[/latex] = ₹ 6,05,000
ప్రతి సంవత్సరం షర్మిల జీతం జాబితా 5,00,000, 5,50,000, 6,05,000 ……………….
[latex]\frac{a_{2}}{a_{1}}=\frac{5,50,000}{5,00,000}=\frac{11}{10}[/latex]

[latex]\frac{a_{3}}{a_{2}}=\frac{6,05,000}{5,50,000}=\frac{11}{10}[/latex]

[latex]\frac{a_{2}}{a_{1}}=\frac{a_{3}}{a_{2}}=\frac{11}{10}[/latex]
కావున షర్మిల యొక్క జీతంతో ఏర్పడే సంఖ్యల జాబితా ఒక గుణశ్రేణి అవుతుంది.

(ii) 30 మెట్లు వున్న ఒక మెట్ల వంతెనలో అన్నింటి కంటే క్రింద ఉన్న మెట్టు నిర్మాణానికి 100 ఇటుకలు అవసరం. ఆ పై ప్రతి పై మెట్టు నిర్మాణానికి దాని క్రింద మెట్టు నిర్మాణానికి కావలసిన వాని ఇటుకల కంటే 2 చొప్పున తక్కువ ఇటుకలు అవసరమైన ప్రతి మెట్టు. నిర్మాణానికి అవసరమయ్యే ఇటుకల సంఖ్యల జాబితా. .
సాధన.
కింది మెట్టు నుండి మెట్ల నిర్మాణానికి అవసరమైన సంఖ్యల జాబితా . 100, 98, 96, 94, ………….. 30 పదాలు
ఇక్కడ [latex]\frac{a_{2}}{a_{1}}=\frac{98}{100}=\frac{49}{50}[/latex];

[latex]\frac{a_{3}}{a_{2}}=\frac{96}{98}=\frac{48}{49}[/latex]

[latex]\frac{a_{2}}{a_{1}} \neq \frac{a_{3}}{a_{2}}[/latex]
కావున పై సంఖ్యల జాబితా గుణశ్రేఢి కాదు.

(iii) 24 సెం.మీ భుజం పొడవు గల ఒక సమబాహు త్రిభుజము యొక్క భుజాల మధ్య బిందువులను కలపటం వల్ల రెండవ త్రిభుజము, దాని భుజాల మధ్య బిందువులను కలపటం వల్ల మూడవ త్రిభుజమేర్పడును. ఈ విధానాన్ని అనంతంగా కొనసాగిస్తే మొదటి, రెండవ, మూడవ … త్రిభుజాల చుట్టుకొలతలు.

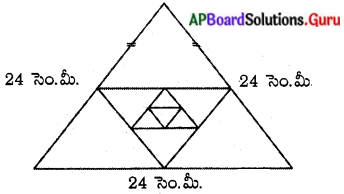
సాధన.
త్రిభుజం యొక్క రెండు భుజాల మధ్య బిందువులు కలిపే రేఖాఖండం మూడవ భుజంలో సగం ఉంటుంది.

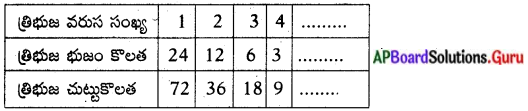
త్రిభుజ చుట్టుకొలతల జాబితా 72, 36, 18, 9,
ఇందులో, [latex]\frac{a_{2}}{a_{1}}=\frac{36}{72}=\frac{1}{2}[/latex]

[latex]\frac{a_{3}}{a_{2}}=\frac{18}{36}=\frac{1}{2}[/latex]

[latex]\frac{\mathrm{a}_{4}}{\mathrm{a}_{3}}=\frac{9}{1.8}=\frac{1}{2}[/latex]

………………
………………
………………
[latex]\frac{\mathrm{a}_{2}}{\mathrm{a}_{1}}=\frac{\mathrm{a}_{3}}{\mathrm{a}_{2}}=\frac{\mathrm{a}_{4}}{\mathrm{a}_{3}}=\ldots .=\frac{1}{2}[/latex]
కావున త్రిభుజాల చుట్టుకొలత జాబితా గుణ శ్రేణిలో ఉంటుంది.

ప్రశ్న 2.
గుణశ్రేణి యొక్క మొదటి పదము a, సామాన్యనిష్పత్తి r లు క్రింద ఇవ్వబడ్డాయి. అయిన మొదటి మూడు పదాలను రాయుము.
(i) a = 4; r= 3.
సాధన. a = 4; r = 3
మొదటి పదం a₁ = a = 4
రెండవ పదం a₂ = ar = 4 × 3 = 12
మూడవ పదం a₂₃ = ar² = 4 (3)²
= 4 × 9 = 36

(ii) a = √5; r = [latex]\frac{1}{5}[/latex]
సాధన.
a = √5 ; r = [latex]\frac{1}{5}[/latex]
మొదటి పదం a₁ = a = √5
రెండవ పదం a₂ = ar = √5 × [latex]\frac{1}{5}[/latex] = [latex]\frac{1}{\sqrt{5}}[/latex]
మూడవ పదం a₃ = ar² = √5 × ([latex]\frac{1}{5}[/latex])²
= √5 × [latex]\frac{1}{25}[/latex] = [latex]\frac{1}{5 \sqrt{5}}[/latex].

(iii) a = 81; r = – [latex]\frac{1}{3}[/latex]
సాధన.
a = 81; r = – [latex]\frac{1}{3}[/latex]
మొదటి పదం a₁ = a = 81
రెండవ పదం a₂ = ar = 81 (- [latex]\frac{1}{3}[/latex]) = – 27
మూడవ పదం a₃ = ar² = 81 × (- [latex]\frac{1}{3}[/latex])²
= 81 ([latex]\frac{1}{9}[/latex]) = 9

(iv) a = [latex]\frac{1}{67}[/latex]; r = 2.
సాధన.
a = [latex]\frac{1}{64}[/latex]; r = 2
a₁ = a = [latex]\frac{1}{64}[/latex]
a₂ = ar = [latex]\frac{1}{64}[/latex] x 2 = 1
a₃ = ar² = [latex]\frac{1}{64}[/latex] × 2² _ 1 _1
= [latex]\frac{1}{64}[/latex] × 4 = 16.

ప్రశ్న 3.
క్రింది వానిలో ఏవి గుణశ్రేఢులు ? గుణశ్రేఢి అయితే తరువాత వచ్చే మూడు పదాలను రాయుము.
(i) 4, 8, 16, ……….
సాధన.
[latex]\frac{a_{2}}{a_{1}}=\frac{8}{4}[/latex] = 2 మరియు [latex]\frac{a_{3}}{a_{2}}=\frac{16}{8}[/latex] = 2
∴ r = [latex]\frac{a_{2}}{a_{1}}=\frac{a_{3}}{a_{2}}[/latex] = 2
కావున గుణశ్రేణి అవుతుంది.
తరువాత 3 పదాలు
[∵ 16 × 2 = 32
32 × 2 = 64
64 × 2 = 128]

(ii) [latex]\frac{1}{3}[/latex], [latex]-\frac{1}{6}[/latex], [latex]\frac{1}{12}[/latex], ……………
సాధన.
[latex]\frac{a_{2}}{a_{1}}=\frac{\frac{-1}{6}}{\frac{1}{3}}=\frac{-1}{6} \times \frac{3}{1}-\frac{-1}{2}[/latex]

[latex]\frac{a_{3}}{a_{2}}=\frac{\frac{1}{12}}{\frac{-1}{6}}=\frac{1}{12} \times \frac{-6}{1} \cdot \frac{-1}{2}[/latex]

[latex]\frac{a_{2}}{a_{1}}=\frac{a_{3}}{a_{2}}[/latex] కావున గుణశ్రేణి అవుతుంది.
తరువాత 3 పదాలు, [latex]-\frac{1}{24}[/latex], [latex]\frac{1}{48}[/latex], [latex]-\frac{1}{96}[/latex]
[∵ [latex]\frac{1}{12} \times\left(\frac{-1}{2}\right)=\frac{-1}{24}[/latex]

[latex]\left(\frac{-1}{24}\right) \times\left(\frac{-1}{2}\right)=\frac{1}{48}[/latex]

[latex]\frac{1}{48} \times\left(\frac{-1}{2}\right)=-\frac{1}{96}[/latex]].

(iii) 5, 55, 555, ……………….
సాధన.
[latex]\frac{a_{2}}{a_{1}}=\frac{55}{5}[/latex] = 11 మరియు [latex]\frac{a_{3}}{a_{2}}=\frac{555}{55}=\frac{111}{11}[/latex]
[latex]\frac{a_{2}}{a_{1}} \neq \frac{a_{3}}{a_{2}}[/latex]కావున గుణశ్రేణి కాదు.

(iv) – 2, – 6, – 18, ……
సాధన.
[latex]\frac{a_{2}}{a_{1}}=\frac{-6}{-2}[/latex] = 3 మరియు [latex]\frac{a_{3}}{a_{2}}=\frac{-18}{-6}[/latex] = 3

[latex]\frac{a_{2}}{a_{1}}=\frac{a_{3}}{a_{2}}[/latex] = 3
కావున ఇది గుణశ్రేణి అవుతుంది
a₄ = a .r³ = (- 2) × 3³ = – 2 × 27 = – 54
a₅ = a .r⁴ = (- 2) × 3⁴ = – 2 × 81 = – 162
a₆ = a .r⁵ = (- 2) × 3⁵ = – 2 × 243 = – 486
తరువాత మూడు పదాలు : – 54, – 162, – 486.

(v) [latex]\frac{1}{42}[/latex], [latex]\frac{1}{4}[/latex], [latex]\frac{1}{6}[/latex], …………
సాధన.
[latex]\frac{a_{2}}{a_{1}}=\frac{\frac{1}{4}}{\frac{1}{2}}=\frac{1}{4} \times \frac{2}{1}=\frac{1}{2}[/latex]

[latex]\frac{a_{3}}{a_{2}}=\frac{\frac{1}{6}}{\frac{1}{4}}=\frac{1}{6} \times \frac{4}{1}=\frac{2}{3}[/latex]

[latex]\frac{a_{2}}{a_{1}} \neq \frac{a_{3}}{a_{2}}[/latex] కావున ఇది గుణశ్రేణి కాదు.

(vi) 3, – 3², 3³, ……….
సాధన.
[latex]\frac{a_{2}}{a_{1}}=\frac{-3^{2}}{3}[/latex] = – 3; [latex]\frac{a_{3}}{a_{2}}=\frac{3^{3}}{-3^{2}}[/latex] = – 3
[latex]\frac{a_{2}}{a_{1}}=\frac{a_{3}}{a_{2}}[/latex] = – 3కావున ఇది గుణ శ్రేణి.
తరువాత వచ్చు మూడు పదాలు . – 3⁴, 3⁵, – 3⁶
[∵ 3³ × – 3 = -3⁴
(- 3)⁴ × (- 3) = 3⁵
3⁵ × (- 3) = – 3⁶].

(vii) x, 1, [latex]\frac{1}{x}[/latex],…………….. (x ≠ 0)
సాధన.
[latex]\frac{a_{2}}{a_{\Gamma}}=\frac{1}{x}[/latex]; [latex]\frac{a_{3}}{a_{2}}=\frac{\frac{1}{x}}{1}=\frac{1}{x}[/latex]
[latex]\frac{a_{2}}{a_{1}}=\frac{\dot{a}_{3}}{a_{2}}=\frac{1}{x}[/latex]కావున ఇది గుణశ్రేణి అవుతుంది
తరువాత మూడు పదాలు [latex]\frac{1}{x^{2}}[/latex], [latex]\frac{1}{x^{3}}[/latex], [latex]\frac{1}{x^{4}}[/latex]
[∵ [latex]\frac{1}{x} \times \frac{1}{x}=\frac{1}{x^{2}}[/latex]
[latex]\frac{1}{x^{2}} \times \frac{1}{x}=\frac{1}{x^{3}}[/latex]
[latex]\frac{1}{x^{3}} \times \frac{1}{x}=\frac{1}{x^{4}}[/latex]]

(viii) [latex]\frac{1}{\sqrt{2}}[/latex], 2, [latex]\frac{8}{\sqrt{2}}[/latex], …………….
సాధన.
[latex]\frac{a_{2}}{a_{1}}=\frac{-2}{\frac{1}{\sqrt{2}}}[/latex] = – 2√2

[latex]\frac{a_{3}}{a_{2}}=\frac{\frac{8}{\sqrt{2}}}{-2}=\frac{8}{\sqrt{2}} \times \frac{-1}{2}=\frac{-4}{\sqrt{2}}[/latex] = 2√2

[latex]\frac{a_{1}}{a_{2}}=\frac{a_{3}}{a_{2}}[/latex] = 2√2 కావున ఇది గుణశ్రేణి.
తరువాత మూడు పదాలు : – 16, 32√2 , – 128
[4√2 × (- 2√2) = -16
(- 16) × (- 2√2) = 32√2
32√2 × (- 2√2) = – 128].

(ix) 0.4, 0.04, 0.004, ……….
సాధన.
0.4, 0.04, 0.004) …. (లేదా) [latex]\frac{4}{10}[/latex], [latex]\frac{4}{100}[/latex], [latex]\frac{4}{1000}[/latex]………
[latex]\frac{a_{2}}{a_{1}}=\frac{0.04}{0.4}[/latex] = [latex]\frac{4}{40}=\frac{1}{10}[/latex]

[latex]\frac{a_{3}}{a_{2}}=\frac{0.004}{0.04}[/latex] = [latex]\frac{4}{40}=\frac{1}{10}[/latex]

∴ [latex]\frac{a_{2}}{a_{1}}=\frac{a_{3}}{a_{2}}=\frac{1}{10}[/latex]

[latex]\frac{a_{2}}{a_{1}}=\frac{\frac{4}{100}}{\frac{4}{10}}[/latex] = [latex]\frac{4}{100} \times \frac{10^{*}}{4}=\frac{1}{10}[/latex]

[latex]\frac{a_{3}}{a_{2}}=\frac{\frac{4}{1000}}{\frac{4}{100}}[/latex] = [latex]\frac{4}{1000} \times \frac{100}{4}=\frac{1}{10}[/latex]

∴ [latex]\frac{a_{2}}{a_{1}}=\frac{a_{3}}{a_{2}}=\frac{1}{10}[/latex]
∴ తరువాత మూడు పదాలు . – 0.0004, 0.00004, 0.000004.

ప్రశ్న 4.
x, x + 2, x + 6 లు ఒక గుణ శ్రేణిలో మూడు వరుస పదాలైన x విలువను కనుగొనుము.
సాధన.
x, x + 2, x + 6 లు ఒక గుణ శ్రేణిలో వరుస పదాలు
[latex]\frac{x+2}{x}=\frac{x+6}{x+2}[/latex]
(x + 2)² = x(x + 6)
x² + 4x + 4 = x² + 6x
x² + 4x – x² – 6x = 4
– 2x = – 4
2x = 4
x = [latex]\frac{4}{2}[/latex] = 2.

సరిచూచుట :
x, x + 2, x + 6
2, 4, 8లు G.P. లో కలవు.