AP Board 10th Class Maths Solutions Chapter 3 బహుపదులు Exercise 3.3

SCERT AP 10th Class Maths Textbook Solutions Chapter 3 బహుపదులు Exercise 3.3 Textbook Exercise Questions and Answers.

AP State Syllabus 10th Class Maths Solutions 3rd Lesson బహుపదులు Exercise 3.3

ప్రశ్న 1.
కింది వర్గ బహుపదులకు శూన్యాలను కనుగొని బహుపది గుణకాలకు; శూన్యాలకు గల సంబంధాన్ని సరిచూడండి.
సాధన.
(i) x² – 2x – 8
(ii) 4s² – 4s + 1
(iii) 6x² -3-7x
(iv) 4u² + 8u
(v) t² – 15
(vi) 3x² – x – 4
సాధన.
(i) x² – 2x – 8
p(x) = x² – 2x – 8 = 0 అయిన

⇒ x² – 4x + 2x – 8 = 0
⇒ x(x – 4) + 2 (x – 4) = 0
⇒ (x – 4) (x + 2) = 0
⇒ x – 4 = 0 లేదా x + 2 = 0
⇒ x = 4 లేదా x = – 2
p(x) శున్య విలువలు α = 4, β = – 2
శూన్య విలువల మొత్తం
(α + β) = 4 + (-2) = 2 = -([latex]\frac{-2}{1}[/latex])
=
శూన్య విలువల లబ్ధం
α . β = (4) (- 2) = – 8 = ([latex]-\frac{8}{1}[/latex])
=

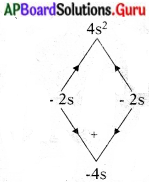
(ii) 4s² – 4s + 10
p(s) = 4s² – 4s + 1 = 0 అయిన
⇒ 4s² – 2s – 2s + 1 = 0
⇒ 2s(2s – 1) – 1 (2s – 1) = 0
⇒ (2s – 1) (2s – 1) = 0
⇒ 2s – 1 = 0 లేదా 2s – 1 = 0
⇒ 2s = 1 లేదా 2s = 1
⇒ s = [latex]\frac{1}{2}[/latex] లేదా s = [latex]\frac{1}{2}[/latex]

శూన్య విలువలు α = [latex]\frac{1}{2}[/latex], β = [latex]\frac{1}{2}[/latex]
శూన్య విలువల మొత్తం (α + β) = [latex]\frac{1}{2}[/latex] + [latex]\frac{1}{2}[/latex] = 1 = [latex]\frac{-(-4)}{4}[/latex]

=

శూన్య విలువల లబ్దం
α . β = [latex]\frac{1}{2}[/latex] . [latex]\frac{1}{2}[/latex] = [latex]\frac{1}{4}[/latex] =

(iii) 6x² – 3 – 7x
p(x) = 6x² – 7x – 3 = 0 అయిన

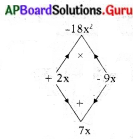
⇒ 6x² + 2x – 9x – 3 = 0
⇒ 2x(3x + 1) – 3 (3x + 1) = 0
⇒ (3x + 1) (2x – 3) = 0
⇒ 3x + 1 = 0 లేదా 2x – 3 = 0
⇒ x = [latex]-\frac{1}{3}[/latex], లేదా x = [latex]\frac{3}{2}[/latex],
శూన్య విలువలు α = [latex]-\frac{1}{3}[/latex], β = [latex]\frac{3}{2}[/latex],
శూన్య విలువల మొత్తం (α + β) = [latex]\frac{-1}{3}+\frac{3}{2}[/latex]
[latex]\frac{-2+9}{6}=\frac{7}{6}=\frac{-(-7)}{6}[/latex] =
శూన్య విలువల లబ్దం α . β = [latex]-\frac{1}{3} \times \frac{3}{2}=\frac{-3}{6}[/latex]
=

(iv) 4u² + 8u
p(u) = 4u² + 8u = 0 అయిన
4u (u + 2) = 0
4u = 0 లేదా u + 2 = 0
u = 0 లేదా u = – 2
శూన్య విలువలు α = 0 మరియు β = -2
శూన్య విలువల మొత్తం
α + β = 0 + (- 2) = – 2 = – [latex]\frac{8}{4}[/latex]
=

శూన్య విలువల లబ్దం
α . β = 0 (- 2) = 0 = [latex]\frac{0}{4}[/latex]
=

(v) t² – 15
p(t) = t² – 15 = 0 అయిన
⇒ t² = 15 = t = ± [latex]\sqrt{15}[/latex]
శూన్య విలువలు α = [latex]\sqrt{15}[/latex] మరియు β = – [latex]\sqrt{15}[/latex]
శూన్య విలువల మొత్తం
α + β = [latex]\sqrt{15}[/latex] + (-[latex]\sqrt{15}[/latex]) = 0
= [latex]\frac{0}{1}[/latex] =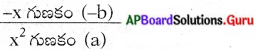

శూన్య విలువల లబ్ధం
α . β = [latex]\sqrt{15}[/latex] × (-[latex]\sqrt{15}[/latex]) = – 15
= [latex]\frac{-15}{1}[/latex] =

(vi) 3x² – x – 4
p(x) = 3x² – x – 4 = 0 అయిన

⇒ 3x² – 4x + 3x – 4 = 0
⇒ x(3x – 4) + 1 (3x – 4) = 0
⇒ (3x – 4) (x + 1) = 0
⇒ 3x – 4 = 0 లేదా x + 1 = 0
⇒ 3x = 4 లేదా x = – 1
⇒ x = [latex]\frac{4}{3}[/latex] లేదా x = – 1
శూన్య విలువలు α = [latex]\frac{4}{3}[/latex] మరియు β = – 1
శూన్య విలువల మొత్తం (α + β) = [latex]\frac{4}{3}[/latex] + (- 1) = [latex]\frac{4-3}{3}=\frac{1}{3}[/latex]
= [latex]\frac{-(-1)}{3}[/latex]
=

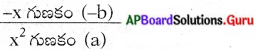
శూన్య విలువల లబ్ధం
α . β = [latex]\frac{4}{3}[/latex] (- 1) = – [latex]\frac{4}{3}[/latex]
=

ప్రశ్న 2.
ఒక వర్గ బహుపది యొక్క శూన్యాల మొత్తము మరియు లబ్దాలు వరుసగా ఇవ్వబడినవి. ప్రతి సందర్భంలోనూ ఆయా వర్గ బహుపదులను కనుగొనండి.
(i) [latex]\frac{1}{4}[/latex], – 1
(ii) √2, [latex]\frac{1}{3}[/latex]
(iii) 0, √5
(iv) 1, 1
(v) -[latex]\frac{1}{4}[/latex], [latex]\frac{1}{4}[/latex]
(vi) 4, 1
సాధన.
(i) శూన్య విలువలు α, β అనుకొనుము.
శూన్య విలువల మొత్తం α + β = [latex]\frac{1}{4}[/latex]
శూన్య విలువల లబ్దం α . β = – 1
α, β లు శూన్య విలువలుగా గల వర్గ బహుపది p(x) = k [x² – (α + β) x + αβ]
కావలసిన వర్గ బహుపది p(x) = k [x² – ([latex]\frac{1}{4}[/latex]) x + (- 1)]
= k [x² – [latex]\frac{x}{4}[/latex] – 1]
= k [latex]\left[\frac{4 x^{2}-x-4}{4}\right][/latex]
k = 4 అయిన p(x) = 4 [latex]\left[\frac{4 x^{2}-x-4}{4}\right][/latex]
p(x) = 4x² – x – 4

(ii) √2, [latex]\frac{1}{3}[/latex]
α + β = √2; αβ = [latex]\frac{1}{3}[/latex]
p(x) = k [x² – (α + β) x + αβ]
= k [x² – √2x + [latex]\frac{1}{3}[/latex]]
= k [latex]\left[\frac{3 x^{2}-3 \sqrt{2} x+1}{3} \underline{1}\right][/latex]
∴ k = 3 అయిన p(x) = 3x^{2</sup – 3√2x + 1}

(iii) 0, √5
α + β = 0, αβ = √5
p(x) = k [x² – (α + β) x + αβ]
= k [x² – 0x + √5]
= k [x² + √5]
∴ k = 1 అయిన p(x) = x² + √5.

(iv) 1, 1
α + β = 1, αβ = 1
p(x) = k [x² – (α + β) x + αβ]
= k [x² – x + 1]
∴ k = 1 అయిన p(x) = x² – x + 1.

(v) – [latex]\frac{1}{4}[/latex], [latex]\frac{1}{4}[/latex]
α + β = – [latex]\frac{1}{4}[/latex]; αβ = [latex]\frac{1}{4}[/latex]
p(x) = k [x² – (α + β) x + αβ]
= k [x² – (- [latex]\frac{1}{4}[/latex]) x + [latex]\frac{1}{4}[/latex]]
= k [x² + [latex]\frac{x}{4}[/latex] + [latex]\frac{1}{4}[/latex]]
= k [latex]\left[\frac{4 x^{2}+x+1}{4}\right][/latex]
∴ k = 4 అయిన p(x) = 4x² + x + 1.

(vi) 4, 1
α + β = 4; αβ = 1
p(x) = k [x² – (α + β) x + αβ]
= k [x² – 4x + 1].
∴ k = 1 అయిన p(x) = x² – 4x + 1

Note:
పై సమస్యలలో k యొక్క వివిధ విలువలకి వివిధ బహుపదులు వస్తాయి.

ప్రశ్న 3.
ఒక వర్గ బహుపది యొక్క శూన్యాలు α, β లు దిగువ ఇవ్వబడినవి. ప్రతి సందర్భంలోనూ ఆయా బహుపదులను కనుగొనండి.

(i) 2, -1
(ii) √3, – √3
(iii) [latex]\frac{1}{4}[/latex], – 1
(iv) [latex]\frac{1}{2}[/latex], [latex]\frac{3}{2}[/latex]
సాధన.
(i) 2, – 1
α = 2 మరియు β = – 1
α + β = 2 + (- 1) = 1
α . β = 2(- 1) = – 2
వర్గ బహుపది
p(x) = k [x² – (α + β) x + αβ]
= k [x² – x + (- 2)]
∴ k = 1 అయిన p(x) = x² – x – 2.

(ii) √3, – √3
α = √3 మరియు β = – √3
α + β = √3 + (- √3) = 0
αβ = (√3) (- √3) = – 3
వర్గ బహుపది
p(x) = k [x² – (α + β) x + αβ)
= k [x² – 0x – 3]
∴ k = 1 అయిన p(x) = x² – 3.

(iii) [latex]\frac{1}{4}[/latex], – 1
α = [latex]\frac{1}{4}[/latex] మరియు β = – 1
α + β = [latex]\frac{1}{4}[/latex] + (- 1)
= [latex]\frac{1-4}{4}=\frac{-3}{4}[/latex]
α. β = ([latex]\frac{1}{4}[/latex]) (- 1) = – [latex]\frac{1}{4}[/latex]
వర్గ బహుపది
p(x) = k [x² – (α + β) x + αβ]
= k[x² – [latex]-\frac{3}{4}[/latex] x + (- [latex]\frac{1}{4}[/latex])]
= [latex]\left[\frac{4 x^{2}+3 x-1}{4}\right][/latex]
∴ k = 4 అయిన p(x) = 4x² + 3x – 1.

(iv) [latex]\frac{1}{2}[/latex], [latex]\frac{3}{2}[/latex]
α = [latex]\frac{1}{2}[/latex], β = [latex]\frac{3}{2}[/latex]
α + β = [latex]\frac{1}{2}+\frac{3}{2}=\frac{4}{2}[/latex] = 2
αβ = ([latex]\frac{1}{2}[/latex]) ([latex]\frac{3}{2}[/latex]) = [latex]\frac{3}{4}[/latex]
వర్గ బహుపది
p(x) = k [x² – (α + β) x + αβ]
= k [x² – 2x + [latex]\frac{3}{4}[/latex]]
= k [latex]\left[\frac{4 x^{2}-8 x+3}{4}\right][/latex]
k = 4 అయిన p(x) = 4x² – 8x + 3.

ప్రశ్న 4.
ఒక ఘన బహుపది x³ + 3x² – x – 3 యొక్క శూన్యాలు 1, – 1 మరియు – 3 అగునని సరిచూడండి. ఇదే విధంగా బహుపది గుణకాలకు, శూన్యాలకు మధ్యగల సంబంధాన్ని సరిచూడండి.
సాధన.
p(x) = x³ + 3x² – x – 3
p(1) = (1)³ + 3(1)² – (1) – 3
= 1 + 3 – 1 – 3
= 4 – 4
p(1) = 0 …………………(1)
p(- 1) = (- 1)³ + 3(- 1)² – (- 1) – 3
= – 1 + 3 + 1 – 3
= – 4 + 4
p(- 1) = 0 ……………..(2)
p(- 3) = (- 3)³ + 3 (- 3)² – (- 3) – 3
= – 27 + 27 + 3 – 3
= -30 + 30
p(-3) = 0 …………… (3)
(1), (2) మరియు (3) ల నుండి
p(1) = 0
p(- 1) = 0
p(- 3) = 0
కావున p(x) కు 1, – 1, – 3 లు శూన్య విలువలు అవుతాయి.
శూన్య విలువల మొత్తం
α + β + γ = 1 + (- 1) + (- 3)
= – 3
= [latex]\frac{-3}{1}[/latex]
=

రెండేసి శూన్య విలువల లబ్దాల మొత్తం :
αβ + βγ + αγ = (1) (- 1) + (- 1) (- 3) + (1) (- 3)
= – 1 + 3 – 3
= – 1
= [latex]\frac{-1}{1}[/latex]
=
శూన్య విలువల లబ్ధం αβγ = (1) (-1) (-3)
= 3
= -([latex]\frac{-3}{1}[/latex])
=