AP Board 10th Class Maths Solutions Chapter 11 త్రికోణమితి Optional Exercise

SCERT AP 10th Class Maths Textbook Solutions Chapter 11 త్రికోణమితి Optional Exercise Textbook Exercise Questions and Answers.

AP State Syllabus 10th Class Maths Solutions 11th Lesson త్రికోణమితి Optional Exercise

ప్రశ్న 1.
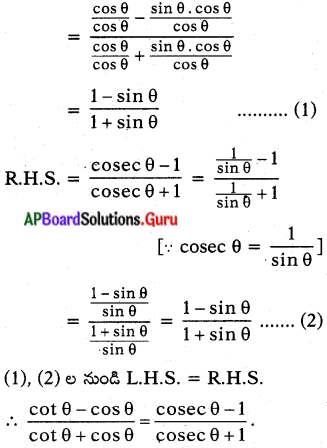
[latex]\frac{\cot \theta-\cos \theta}{\cot \theta+\cos \theta}=\frac{cosec \theta-1}{cosec \theta+1}[/latex] అని నిరూపించండి.
సాధన.

ప్రశ్న 2.
[latex]\frac{\sin \theta-\cos \theta+1}{\sin \theta+\cos \theta-1}=\frac{1}{\sec \theta-\tan \theta}[/latex] నిరూపించండి.
(sec² θ = 1 + tan² θ)
సాధన.
L.H.S.= [latex]\frac{\sin \theta-\cos \theta+1}{\sin \theta+\cos \theta-1}=\frac{1}{\sec \theta-\tan \theta}[/latex]
లవ, హారాలను cos θ చే భాగించగా
= [latex]\frac{\frac{\sin \theta}{\cos \theta}-\frac{\cos \theta}{\cos \theta}+\frac{1}{\cos \theta}}{\frac{\sin \theta}{\cos \theta}+\frac{\cos \theta}{\cos \theta}-\frac{1}{\cos \theta}}[/latex]

= [latex]\frac{\tan \theta+\sec \theta-1}{\tan \theta-\sec \theta+1}[/latex]

= [latex]\frac{(\tan \theta+\sec \theta)-\left(\sec ^{2} \theta-\tan ^{2} \theta\right)}{\tan \theta+1-\sec \theta}[/latex]
[∵ 1 = sec² θ – tan² θ]

ప్రశ్న 3.
(cosec A – sin A) (sec A – cos A) = [latex]\frac{1}{\tan A+\cot A}[/latex] అని నిరూపించండి.
సాధన.
L.H.S.= (cosec A – sin A) (sec A – cos A)
= ([latex]\frac{1}{\sin A}[/latex] – sin A) ([latex]\frac{1}{\cos A}[/latex] – cos A)
[∵ cosec A = [latex]\frac{1}{\sin A}[/latex]; sec A = [latex]\frac{1}{\cos A}[/latex])
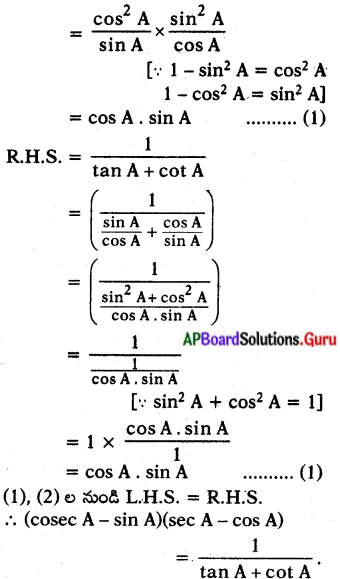
= [latex]\left(\frac{1-\sin ^{2} A}{\sin A}\right)\left(\frac{1-\cos ^{2} A}{\cos A}\right)[/latex]

=

ప్రశ్న 4.
[latex]\frac{1+\sec A}{\sec A}=\frac{\sin ^{2} A}{1-\cos A}[/latex] అని నిరూపించండి.
సాధన.
L.H.S = [latex]\frac{1+\sec A}{\sec A}[/latex]
= [latex]\frac{1}{\sec A}+\frac{\sec A}{\sec A}[/latex]
= cos A + 1
= [latex]\frac{(\cos A+1)(\cos A-1)}{(\cos A-1)}[/latex] (అకరణీయం చేయగా)
= [latex]\frac{\cos ^{2} A-1}{\cos A-1}[/latex]
= [latex]\frac{-1\left(1-\cos ^{2} A\right)}{-1(1-\cos A)}[/latex]
= [latex]\frac{1-\cos ^{2} A}{1-\cos A}=\frac{\sin ^{2} A}{1-\cos A}[/latex] = R.H.S
[∵ 1 – cos² A = sin² A]
∴ LHS = RHS అని నిరూపించబడినది.

ప్రశ్న 5.
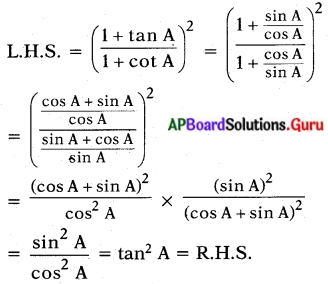
[latex]\left(\frac{1+\tan ^{2} A}{1+\cot ^{2} A}\right)=\left(\frac{1+\tan A}{1+\cot A}\right)^{2}[/latex] = tan² A అని చూపండి.
సాధన.
L.H.S. = [latex]\left(\frac{1+\tan ^{2} \mathrm{~A}}{1+\cot ^{2} \mathrm{~A}}\right)=\frac{\sec ^{2} \mathrm{~A}}{cosec^{2} \mathrm{~A}}[/latex]
[∵ 1 + tan² A = sec² A;
1 + cot² A = cosec² A]
= [latex]\frac{\frac{1}{\cos ^{2} A}}{\frac{1}{\sin ^{2} A}}[/latex]
[∵ sec A = 1/cos A
cosec A = 1/sin A]
= [latex]\frac{1}{\cos ^{2} A} \times \frac{\sin ^{2} A}{1}[/latex]
= [latex]\frac{\sin ^{2} A}{\cos ^{2} A}[/latex]
= tan² A
= R.H.S.

ప్రశ్న 6.
[latex]\left(\frac{\sec A-1}{\sec A+1}\right)=\left(\frac{1-\cos A}{1+\cos A}\right)[/latex] అని నిరూపించండి.
సాధన.
L.H.S. = [latex]\frac{\sec A-1}{\sec A+1}=\frac{\frac{1}{\cos A}-1}{\frac{1}{\cos A}+1}[/latex]

= [latex]\frac{\frac{1-\cos A}{\cos A}}{\frac{1+\cos A}{\cos A}}=\frac{1-\cos A}{1+\cos A}[/latex]

= R.H.S
∴ L.H.S. = R.H.S