AP 10th Class Maths Bits Chapter 11 Trigonometry with Answers

Practice the AP 10th Class Maths Bits with Answers Chapter 11 Trigonometry on a regular basis so that you can attempt exams with utmost confidence.

AP State Syllabus 10th Class Maths Bits 11th Lesson Trigonometry with Answers

Question 1.
If cosec θ + cot θ = 2, then cos θ =
A) [latex]\frac{3}{5}[/latex]
B) [latex]\frac{4}{5}[/latex]
C) [latex]\frac{5}{3}[/latex]
D) [latex]\frac{6}{5}[/latex]
Answer:
A) [latex]\frac{3}{5}[/latex]

Question 2.
If 4 cos² θ – 3 = 0, then sin θ =…………………….
A) [latex]\frac{1}{2}[/latex]
B) -[latex]\frac{1}{2}[/latex]
C) [latex]\frac{1}{\sqrt{2}}[/latex]
D) [latex]\frac{\sqrt{3}}{2}[/latex]
Answer:
A) [latex]\frac{1}{2}[/latex]

Question 3.
If cos (A + B) = 0, cos B = [latex]\frac{\sqrt{3}}{2}[/latex] then A =
A) 15°
B) 60°
C) 30°
D) 45°
Answer:
B) 60°

Question 4.
If sec θ + tan θ = [latex]\frac{1}{3}[/latex], then sec θ – tan θ = …………………
A) 3
B) [latex]\frac{1}{3}[/latex]
C) 1
D) 0
Answer:
A) 3

Question 5.
If sin x = [latex]\frac{5}{7}[/latex] , then cosec x = …………………….
A) [latex]\frac{5}{7}[/latex]
B) [latex]\frac{7}{5}[/latex]
C) [latex]\frac{2}{5}[/latex]
D) [latex]\frac{2}{7}[/latex]
Answer:
B) [latex]\frac{7}{5}[/latex]

Question 6.
Given ∠A = 75°, ∠B = 30°, then tan (A-B) = …………………
A) √3
B) [latex]\frac{1}{\sqrt{3}}[/latex]
C) 1
D) [latex]\frac{1}{\sqrt{2}}[/latex]
Answer:
C) 1

Question 7.
Which one of the following is NOT defined?
A) sin 90°
B) cos 0°
C) sec 90°
D) cos 90°
Answer:
C) sec 90°

Question 8.
………………….
A) sin A
B) [latex]\sqrt{\sin A}[/latex]
C) sin²A
D) sin⁴A
Answer:
C) sin²A

Question 9.
tan 36°. tan 54° + sin 30° = ………………..
A) [latex]\frac{3}{2}[/latex]
B) [latex]\frac{1}{2}[/latex]
C) 2
D) [latex]\frac{2}{3}[/latex]
Answer:
A) [latex]\frac{3}{2}[/latex]

Question 10.
If sin A = [latex]\frac{24}{25}[/latex], then sec A = ………………………
A) [latex]\frac{7}{25}[/latex]
B) [latex]\frac{25}{7}[/latex]
C) [latex]\frac{24}{7}[/latex]
D) [latex]\frac{7}{24}[/latex]
Answer:
B) [latex]\frac{25}{7}[/latex]

Question 11.
Values of sin 30°. sin 90°. sec 60° are in …………………
A) A.P.
B) G.P.
C) a
D) (A)or(C)
Answer:
B) G.P.

Question 12.
From the figure : Sin A =

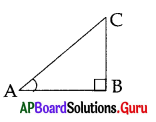
A) [latex]\frac{\mathrm{AC}}{\mathrm{BC}}[/latex]
B) [latex]\frac{\mathrm{BC}}{\mathrm{AC}}[/latex]
C) [latex]\frac{\mathrm{BC}}{\mathrm{AB}}[/latex]
D) [latex]\frac{\mathrm{AC}}{\mathrm{AB}}[/latex]
Answer:
B) [latex]\frac{\mathrm{BC}}{\mathrm{AC}}[/latex]

Question 13.
The value of tan θ in terms of sinθ is
A) [latex]\frac{\sin \theta}{1-\sin ^{2} \theta}[/latex]
B) [latex]\frac{\sqrt{\sin ^{2} \theta-1}}{\sin \theta}[/latex]
C) [latex]\frac{\sin \theta}{\sqrt{1-\sin ^{2} \theta}}[/latex]
D) [latex]\frac{\sqrt{1-\sin ^{2} \theta}}{\sin \theta}[/latex]
Answer:
C) [latex]\frac{\sin \theta}{\sqrt{1-\sin ^{2} \theta}}[/latex]

Question 14.
If cosec θ = 2 and cot θ = [latex]\sqrt{3 \mathbf{p}}[/latex] where ‘θ’ is an acute angle, then p =
A) 2
B) 1
C) [latex]\frac{1}{2}[/latex]
D) √3
Answer:
B) 1

Question 15.
If sec θ = 3K and tan θ = [latex]\frac{3}{K}[/latex], then K² – [latex]\frac{\mathbf{1}}{\mathbf{K}^{2}}[/latex] =
A) 9
B) [latex]\frac{1}{9}[/latex]
C) 3
D) [latex]\frac{1}{3}[/latex]
Answer:
B) [latex]\frac{1}{9}[/latex]

Question 16.
tan θ is not defined when ‘θ’ is
A) 0°
B) 30°
C) 60°
D) 90°
Answer:
D) 90°

Question 17.
It tan θ = [latex]\frac{1}{\sqrt{3}}[/latex], then 7 sin²θ + 3 cos²θ =
A) [latex]\frac{16}{4}[/latex]
B) [latex]\frac{7}{4}[/latex]
C) [latex]\frac{9}{4}[/latex]
D) 1
Answer:
A) [latex]\frac{16}{4}[/latex]

Question 18.
If cos 2θ = sin 4θ, here 2θ, 4θ are acute angles, then the value of ‘θ’ =
A) 60°
B) 30°
C) 45°
D) 15°
Answer:
D) 15°

Question 19.
Values of cos²0° + cos² 60° is
A) [latex]\frac{5}{4}[/latex]
B) [latex]\frac{2}{\sqrt{3}}[/latex]
C) [latex]\frac{1}{\sqrt{2}}[/latex]
D) [latex]\frac{\sqrt{3}}{2}[/latex]
Answer:
A) [latex]\frac{5}{4}[/latex]

Question 20.
If Sin A = Cos B then A + B = ……………………..
A) 60°
B) 90°
C) 45°
D) 120°
Answer:
B) 90°

Question 21.
If 5 tan α = 4, then [latex]\frac{5 \sin \alpha-3 \cos \alpha}{5 \sin \alpha+2 \cos \alpha}[/latex] = ………………….
A) [latex]\frac{1}{7}[/latex]
B) [latex]\frac{1}{6}[/latex]
C) [latex]\frac{2}{5}[/latex]
D) [latex]\frac{3}{7}[/latex])
Answer:
B) [latex]\frac{1}{6}[/latex]

Question 22.
[latex]\sqrt{1+\sin ^{2} \theta+\cos ^{2} \theta}[/latex] = …………………
A) 1
B) 2
C) [latex]\sqrt{21}[/latex]
D) √2
Answer:

Question 23.
tan 2A = 1 then A = …………………..
A) 45.5
B) 60.5
C) 22.5
D) 30.5
Answer:
C) 22.5

Question 24.
If x = a secθ cosΦ, y = b secθ sinΦ. z = c tan θ, then [latex]\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}[/latex] = ………………….
A) [latex]\frac{z^{2}}{c^{2}}[/latex]
B) 1 – [latex]\frac{z^{2}}{c^{2}}[/latex]
C) [latex]\frac{z^{2}}{c^{2}}[/latex] – 1
D) 1 + [latex]\frac{z^{2}}{c^{2}}[/latex]
Answer:
D) 1 + [latex]\frac{z^{2}}{c^{2}}[/latex]

Question 25.
If 7sin²θ + 3 cos²θ = 5, then tan θ = ……………………
A) √3
B) [latex]\frac{1}{\sqrt{3}}[/latex]
C) 1
D) 0
Answer:
C) 1

Question 26.
If sinθ + sin²θ = 1, then cos²θ + cos⁴θ = ……………..
A) -1
B) 1
C) 0
D) None of these
Answer:
B) 1

Question 27.
If cotθ + cosecθ = 5, then cosθ = ………………..
A) [latex]\frac{12}{13}[/latex]
B) [latex]\frac{26}{24}[/latex]
C) [latex]\frac{5}{13}[/latex]
D) [latex]\frac{13}{12}[/latex]
Answer:
A) [latex]\frac{12}{13}[/latex]

Question 28.
[latex]\frac{\cos \theta}{1-\tan \theta}+\frac{\sin \theta}{1-\cot \theta}[/latex] = ………………
A) cos θ – sin θ
B) tan θ – cot θ
C) cos θ – sin θ
D) tan θ + cot θ
Answer:
A) cos θ – sin θ

Question 29.
If tanθ = [latex]\frac{7}{8}[/latex], then the value of [latex]\frac{(1+\sin \theta)(1-\sin \theta)}{(1+\cos \theta)(1-\cos \theta)}[/latex] ……………….
A) [latex]\frac{64}{49}[/latex]
B) [latex]\frac{49}{64}[/latex]
C) [latex]\frac{8}{7}[/latex]
D) [latex]\frac{7}{8}[/latex]
Answer:
A) [latex]\frac{64}{49}[/latex]

Question 30.
If cosecθ + cotθ = P, then value of cosθ = ……………………
A) [latex]\frac{1-P^{2}}{1+P^{2}}[/latex]
B) [latex]\frac{1-\mathrm{P}^{2}}{2 \mathrm{P}}[/latex]
C) [latex]\frac{2 P}{1+P^{2}}[/latex]
D) [latex]\frac{2 \mathrm{P}}{1-\mathrm{P}^{2}}[/latex]
Answer:
A) [latex]\frac{1-P^{2}}{1+P^{2}}[/latex]

Question 31.
If x > y and [latex]\frac{2 x y}{x^{2}+y^{2}}[/latex] = cosθ, then sinθ = ………………….
A) [latex]\frac{x^{2}-y^{2}}{x^{2}+y^{2}}[/latex]
B) [latex]\frac{x^{2}+y^{2}}{x^{2}-y^{2}}[/latex]
C) [latex]\frac{x^{2}-y^{2}}{2 x y}[/latex]
D) [latex]\frac{2 x y}{x^{2}-y^{2}}[/latex]
Answer:
A) [latex]\frac{x^{2}-y^{2}}{x^{2}+y^{2}}[/latex]

Question 32.
If secθ + tanθ = 3, then cosθ = ………………..
A) [latex]\frac{3}{4}[/latex]
B) [latex]\frac{3}{5}[/latex]
C) [latex]\frac{2}{3}[/latex]
D) [latex]\frac{2}{5}[/latex]
Answer:
B) [latex]\frac{3}{5}[/latex]

Question 33.
In ΔABC, if BC = 3, CA = 4, AB = 5, then cos ∠BAC =
A) [latex]\frac{3}{5}[/latex]
B) [latex]\frac{3}{4}[/latex]
C) [latex]\frac{4}{5}[/latex]
D) [latex]\frac{5}{3}[/latex]
Answer:
B) [latex]\frac{3}{4}[/latex]

Question 34.
sin⁶ A + cos⁶ A + 3sin²A cos²A =
A) 1
B) -1
C) 0
D) None
Answer:
A) 1

Question 35.
sin²2 30°, sin² 45° and sin² 60° are in
A) AP
B) GP
C) HP
D) AGP
Answer:
A) AP

Question 36.
If sinθ . cosθ = [latex]\frac {1}{2}[/latex], then θ = …………………
A) 0°
B) 30°
C) 45°
D) 60°
Answer:
C) 45°

Question 37.
If tanθ [latex]\frac {3}{4}[/latex] , then the value of [latex]\frac{1-\cos \theta}{1+\cos \theta}[/latex] =
A) 9
B) [latex]\frac {1}{9}[/latex]
C) 4
D) [latex]\frac {1}{4}[/latex]
Answer:
B) [latex]\frac {1}{9}[/latex]

Question 38.
If A, B and C are interior angles of atriangle ABC, then tan ([latex]\frac{\mathbf{A}+\mathbf{B}}{2}[/latex]) =
A) sin([latex]\frac{\mathrm{C}}{2}[/latex])
B) cos([latex]\frac{\mathrm{C}}{2}[/latex])
C) tan([latex]\frac{\mathrm{C}}{2}[/latex])
D) cot([latex]\frac{\mathrm{C}}{2}[/latex])
Answer:
D) cot([latex]\frac{\mathrm{C}}{2}[/latex])

Question 39.
If cos A = [latex]\frac{12}{13}[/latex], then sin A =
A) [latex]\frac{5}{13}[/latex]
B) [latex]\frac{5}{12}[/latex]
C) [latex]\frac{12}{13}[/latex]
D) [latex]\frac{13}{5}[/latex]
Answer:
A) [latex]\frac{5}{13}[/latex]

Question 40.
=
A) 0
B) 1
C) -1
D) [latex]\frac{1}{2}[/latex]
Answer:
B) 1

Question 41.
If tan2A = cot (A – 18°), where 2A is an acute angle, then A =
A) 6°
B) 18°
C) 36°
D) 54°
Answer:
C) 36°

Question 42.
If x = a cosecθ and y = bcotθ, then b²x² – a²y² =
A) a² + b²
B) a²b²
C) [latex]\frac{a^{2}+b^{2}}{a^{2}-b^{2}}[/latex]
D) None
Answer:
B) a²b²

Question 43.
tan 30°, tan 45°, tan 60° are in
A) AP
B) GP
C) HP
D) None
Answer:
B) GP

Question 44.
cos⁴θ – sin⁴θ =
A) 1 – 2sin²θ
B) 2sin²θ
C) secθ
D) cosecθ
Answer:
A) 1 – 2sin²θ

Question 45.
Sin 0°. Tan 60°. Cos 30°. cosec 45° =
A) 1
B) 0
C) [latex]\frac{\sqrt{3}}{2}[/latex]
D) ∝
Answer:
B) 0

Question 46.
Ifsin(A + B) = [latex]\frac{1}{\sqrt{2}}[/latex] and cos (A – B) = [latex]\frac{1}{\sqrt{2}}[/latex] then ∠B =
A) 60°
B) 45°
C) 30°
D) 0°
Answer:
D) 0°

Question 47.
If sinθ + cosθ = √2 then θ =
A) 0°
C) 45°
B) 30°
D) 60°
Answer:
C) 45°

Question 48.
[latex]\frac{1-\tan ^{2} 30^{\circ}}{1+\tan ^{2} 30^{\circ}}[/latex] = ………………..
A) [latex]\frac{1}{2}[/latex]
B) [latex]\frac{1}{\sqrt{2}}[/latex]
C) [latex]\frac{\sqrt{3}}{2}[/latex]
D) 1
Answer:
A) [latex]\frac{1}{2}[/latex]

Question 49.
cos⁴ θ – sin⁴ θ =
A) cos² θ – sin² θ
B) 2cos² θ – 1
C) 1 – 2sin² θ
D) None
Answer:
A) cos² θ – sin² θ

Question 50.
If x = cos θ + sin θ and y = cos θ – sin θ, then x² + y² =
A) 0
B) 1
C) -1
D) 2
Answer:
D) 2

Question 51.
sin (A + B) cos (A – B) + sin (A – B) cos (A + B) =
A) sin 2A
B) sin 2B
C) cos 2A
D) cos 2B
Answer:
A) sin 2A

Question 52.
If sin A = cos B, then A + B =
A) 45°
B) 60°
C) 90°
B) 75°
Answer:
C) 90°

Question 53.
The value of cos 36° cos 54° – sin 36° sin 54° =
A) 1
B) 0
C) 2
D) -1
Answer:
B) 0

Question 54.
The value of [latex]\frac{1}{1+\cos \theta}+\frac{1}{1-\cos \theta}[/latex] =
A) 2 sec²θ
B) 2secθ
C) 2cosec²θ
D) 2cosecθ
Answer:
C) 2cosec²θ

Question 55.
The value of tan²θ + tan⁴θ
A) sec⁴θ – sec²θ
B) sec²θ – sec⁴θ
C) sin²θ – cos²θ
D) sec²θ – tan²θ
Answer:
A) sec⁴θ – sec²θ

Question 56.
The value of cos 45° . cos 30° . cos 90° . cos 60° =
A) [latex]\frac{\sqrt{3}}{4 \sqrt{2}}[/latex]
B) [latex]\frac{\sqrt{3}}{4}[/latex]
C) 0
D) [latex]\frac{\sqrt{3}}{2 \sqrt{2}}[/latex]
Answer:
C) 0

Question 57.
If x = a cosecθ and y = a cotθ, then which of the following is true ?
A) x² + y² = a²
B) x² – y² = a²
C) x + y = a
D) xy = a
Answer:
D) xy = a

Question 58.
If sin A = [latex]\frac{7}{25}[/latex],then cot A =
A) [latex]\frac{25}{7}[/latex]
B) 1
C) [latex]\frac{24}{25}[/latex]
D) [latex]\frac{24}{7}[/latex]
Answer:
C) [latex]\frac{24}{25}[/latex]

Question 59.
cos 12° – sin 78° = ………………
A) 1
B) 1/2
C) 0
D) -1
Answer:
C) 0

Question 60.
If x = cosce θ + cot θ,.y = cosec θ – cot θ, then which of the following is true ?
A) x + y = 0
B) x – y = 0
C) [latex]\frac{x}{y}[/latex] = 1
D) xy = 1
Answer:
D) xy = 1

Question 61.
Tan²θ – Sec²θ = ………………..
A) 1
B) -1
C) 0
D) ∞
Answer:
B) -1

Question 62.
In Δ ABC, Sin C = [latex]\frac{3}{5}[/latex]. Then Cos A = ……………………..
A) [latex]\frac{3}{5}[/latex]
B) [latex]\frac{4}{5}[/latex]
C) [latex]\frac{5}{4}[/latex]
D) [latex]\frac{5}{3}[/latex]
Answer:
A) [latex]\frac{3}{5}[/latex]

Question 63.
If cot A = [latex]\frac{5}{12}[/latex], then sin A + cos A is ……………….
A) [latex]\frac{17}{13}[/latex]
B) [latex]\frac{12}{13}[/latex]
C) [latex]\frac{5}{13}[/latex]
D) [latex]\frac{20}{13}[/latex]
Answer:
A) [latex]\frac{17}{13}[/latex]

Question 64.
Which of following values is not a possible value of sin x ?
A) [latex]\frac{3}{4}[/latex]
B) [latex]\frac{3}{5}[/latex]
C) [latex]\frac{4}{5}[/latex]
D) [latex]\frac{5}{4}[/latex]
Answer:
D) [latex]\frac{5}{4}[/latex]

Question 65.
Which of the following is not defined ?
A) Tan0°
B) Tan 90°
C) Cot 90°
D) Sec 0°
Answer:
B) Tan 90°

Question 66.
If Sin A = [latex]\frac{24}{25}[/latex] then Cot A = ………………………
A) [latex]\frac{25}{24}[/latex]
B) [latex]\frac{7}{24}[/latex]
C) [latex]\frac{24}{7}[/latex]
D) [latex]\frac{25}{7}[/latex]
Answer:
B) [latex]\frac{7}{24}[/latex]

Question 67.
In ΔPQR, ∠Q = 90°; PQ = 5 cm; PR = 13 cm then QR =
A) 5 cm
B) 12 cm
C) 13 cm
D) 25 cm
Answer:
B) 12 cm

Question 68.
If Sin A = [latex]\frac{3}{5}[/latex] then Cos A =
A) [latex]\frac{3}{4}[/latex]
B) [latex]\frac{4}{5}[/latex]
C) [latex]\frac{5}{4}[/latex]
D) [latex]\frac{4}{3}[/latex]
Answer:
B) [latex]\frac{4}{5}[/latex]

Question 69.
8 Tan A = 15 then Sin A – Cos A =
A) [latex]\frac{7}{3}[/latex]
B) [latex]\frac{7}{17}[/latex]
C) [latex]\frac{9}{14}[/latex]
D) [latex]\frac{3}{7}[/latex]
Answer:
B) [latex]\frac{7}{17}[/latex]

Question 70.
Sin2 60° + Cos2 30° + Tan2 60° =
A) [latex]\frac{9}{2}[/latex]
B) [latex]\frac{2}{9}[/latex]
C) [latex]\frac{1}{9}[/latex]
D) 1
Answer:
A) [latex]\frac{9}{2}[/latex]

Question 71.
Sin θ = [latex]\frac{20}{29}[/latex] then Sin² θ + cos² θ =
A) [latex]\frac{144}{841}[/latex]
B) [latex]\frac{41}{841}[/latex]
C) 1
D) 0
Answer:
C) 1

Question 72.
If θ = 45° then the value of 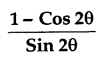is
A) 0
B) 1
C) 2
D) ∞
Answer:
B) 1

Question 73.
In ΔABC if Sin A = [latex]\frac{9}{15}[/latex] then Cosec² A – Cot² A =
A) 1
B) -1
C) 2
D) 3
Answer:
A) 1

Question 74.
(1 + Tan² 45°)² =
A) 1
B) 7
C) 4
D) 9
Answer:
C) 4

Question 75.
Sin²105° + Cos²105° =
A) – 1
B) 1
C) 3
D) 0
Answer:
B) 1

Question 76.
Tan (B + 15°) = [latex]\frac{1}{\sqrt{3}}[/latex] then B =
A) 60°
B) 80°
C) 70°
D) 15°
Answer:
D) 15°

Question 77
Maximum value of Sin θ =
A) 1
B) [latex]\frac{1}{2}[/latex]
C) [latex]\frac{\sqrt{3}}{2}[/latex]
D) [latex]\frac{1}{\sqrt{2}}[/latex]
Answer:
A) 1

Question 78.
If Sec 2A = Cosec (A – 27°), then the value of ∠A is
A) 35°
B) 37°
C) 39°
D) 21°
Answer:
C) 39°

Question 79.
Sin (A – B) = [latex]\frac {1}{2}[/latex]; Cos (A + B) = [latex]\frac {1}{2}[/latex] then ∠A is
A) 60°
C) 30°
B) 15°
D) 45°
Answer:
D) 45°

Question 80.
Tan² 60° + 2 Tan² 45° = x Tan 45° Then x =
A) 0
B) 5
C) 1
D) 2
Answer:
B) 5

Question 81.
Sin θ = Cos θ then θ =
A) 30°
B) 45°
C) 60°
D) 90°
Answer:
B) 45°

Question 82.
Sec θ + Tan θ = p then Sin θ =
A) [latex]\frac{p^{2}-1}{p^{2}+1}[/latex]
B) [latex]\frac{p}{p^{2}+1}[/latex]
C) [latex]\frac{p^{2}-1}{p}[/latex]
D) [latex]\frac{p^{2}+1}{p^{2}-1}[/latex]
Answer:
A) [latex]\frac{p^{2}-1}{p^{2}+1}[/latex]

Question 83.
2 . Sin 30° . Cos 30° =
A) 1
B) [latex]\frac{2}{\sqrt{3}}[/latex]
C) [latex]\frac{\sqrt{3}}{2}[/latex]
D) [latex]\frac{1}{\sqrt{2}}[/latex]
Answer:
C) [latex]\frac{\sqrt{3}}{2}[/latex]

Question 84.
Sin 18° = Cos x, then x =
A) 73°
B) 37°
C) 72°
D) 84°
Answer:
C) 72°

Question 85.
Tan θ + Cot θ = 2, then Sin θ =
A) 3
B) 1
C) √2
D) [latex]\frac{1}{\sqrt{2}}[/latex]
Answer:
D) [latex]\frac{1}{\sqrt{2}}[/latex]

Question 86.
The value of Cos 0° + Sin 90° + √2 Sin 45° =
A) 5
C) 1
B) 4
D) 3
Answer:
D) 3

Question 87.
Sin θ = [latex]\frac {1}{2}[/latex] then cot θ =
A) 3
B) 7
C) √3
D) 2√3
Answer:
C) √3

Question 88.
In ΔABC, a = 3 units; b = 4 units; c = 5 units. Then cos A =
A) [latex]\frac{3}{5}[/latex]
B) [latex]\frac{3}{4}[/latex]
C) [latex]\frac{5}{3}[/latex]
D) [latex]\frac{4}{5}[/latex]
Answer:
D) [latex]\frac{4}{5}[/latex]

Question 89.
Cos (A – B) = [latex]\frac{1}{2}[/latex]; Sin B = [latex]\frac{1}{\sqrt{2}}[/latex] , then the value of A.
A) 15°
B) 105°
C) 90°
D) 60°
Answer:
B) 105°

Question 90.
Sin 60° Cos 30° + Cos 60° Sin 30° Value is ……………………
A) [latex]\frac{1}{2}[/latex]
B) 1
C) [latex]\frac{\sqrt{3}}{2}[/latex]
D) [latex]\frac{2}{\sqrt{3}}[/latex]
Answer:
B) 1

Question 91.
√3 Tan θ = 1, then θ =
A) 30°
B) 45°
C) 60°
D) 90°
Answer:
A) 30°

Question 92.
In a ΔABC if ∠B = 90° and Tan C = [latex]\frac {5}{12}[/latex] , then the length of the hypotenuse is
A) 6
B) 13
C) 21
D) 17
Answer:
B) 13

Question 93.
Tan² 60° + 4 Cos² 45° + 3 Sec² 30° + 5 Cos² 90° =
A) 7
B) 8
C) 9
B) 10
Answer:
A) 7

Question 94.
Sec² 27° – Cot² 63° =
A) 3
B) 0
C) 1
D) 2
Answer:
B) 0

Question 95.
=
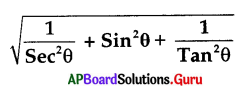A) Sin θ
B) Cos θ
C) Sec θ
D) Cosec θ
Answer:
D) Cosec θ

Question 96.
Sin² θ (1 + Cot²θ) =
A) Cos² θ
B) Sec² θ
C) Tan² θ
D) 1
Answer:
D) 1

Question 97.
If A = 45°, then (1 + Tan A) (1 + Tan²A) (1 + Tan³ A) =
A) 6
B) 8
C) 4
D) 2
Answer:
B) 8

Question 98.
Sin² θ . Cot² θ + Cos² θ . Tan² θ =
A) 0
B) 2
C) 1
D) -1
Answer:
C) 1

Question 99.
Tan 45° + 2 Tan² 60° =
A) 6
B) 7
C) 8
D) 9
Answer:
B) 7

Question 100.
Sin 2A = 2 Sin A, then ∠A =
A) 0°
B) 30°
C) 45°
D) 60°
Answer:
A) 0°

Question 101.
If x Sin (90° – θ) Cot (90° – θ) = Cos (90° – θ) then x =
A) 0
B) 1
C) – 1
D) 2
Answer:
B) 1

Question 102.
If Tan θ + Cot θ = 5, then the value of Tan² θ + Cot² θ =
A) 25
B) 23
C) 27
D) 15
Answer:
B) 23

Question 103.
If Cosec θ – Cot θ = [latex]\frac {1}{4}[/latex] then the value of Cosec θ + Cot θ is
A) 1
B) -1
C) [latex]\frac {1}{4}[/latex]
D) 4
Answer:
D) 4

Question 104.
Sin 40°=
A) Sin × 40°
B) Sin + 40°
C) Sin 20° + Sin 20°
D) A real number
Answer:
D) A real number

Question 105.
If ΔXYZ is a right angled isosceles triangle and ∠Y = 90° then XZ =
A) √2 XY
B) √3 XY
C) 2 XY
D) XY²
Answer:
A) √2 XY

Question 106.
Tan θ is not defined, then θ =
A) 50°
B) 60°
C) 180°
D) 90°
Answer:
D) 90°

Question 107.
Sin (90° – θ) =
A) Sin θ
B) Cos θ
C) Cosec θ
D) Sec θ
Answer:
B) Cos θ

Question 108.
Tan 81° =
A) Cos 9°
B) Sin 9°
C) Cot 9°
D) Tan 9°
Answer:
C) Cot 9°

Question 109.
Sin A. Cos (90° – A) + Cos A. Sin (90° – A) =
A) Sin²A
B) Cos²A
C) 0
D) 1
Answer:
D) 1

Question 110.
=
A) Tan² θ
B) Cot² θ
C) Sin² θ
D) Cos² θ
Answer:
A) Tan² θ

Question 111.
a) Sin (A + B) = Sin A Cos B + Cos A Sin B
b) Sin (A – B) = Sin A Cos B – Cos A Sin B
Which is correct in the above statements?
A) a is correct
B) b is correct
C) Both a and b are correct
D) Both a and b are wrong
Answer:
C) Both a and b are correct

Question 112.
a) Sin 30° = 1
b) Cos 30° = [latex]\frac {1}{2}[/latex]
Which is correct in the above statements?
A) a is correct
B) Both a and b are correct
C) b is correct
D) Both a and b are wrong
Answer:
D) Both a and b are wrong

Question 113.
a) Sin² θ + Cos² θ = 1
b) Tan² θ + Sec² θ = 1
Which is correct in the above statements?
A) b is correct
B) a is correct
C) Both a and b are correct
D) Both a and b are wrong
Answer:
B) a is correct

Question 114.
Sin (A – B) = [latex]\frac {1}{2}[/latex]; Cos (A + B) = [latex]\frac {1}{2}[/latex] is true for ……………….
A) 0° > A + B > 90°
B) A > B
C) 0°< A + B < 90°and A > B
D) A < B and A > B
Answer:
C) 0°< A + B < 90°and A > B

Question 115.
Sin 81° + Tan 81° can be expressed as …………………..
A) Sin 9° + Tan 9°
B) cos 9° + cot 9°
C) Sin 9° + Cot 9°
D) Cos 9° + Tan 9°
Answer:
B) cos 9° + cot 9°

Question 116.
Sin (A + B) = Sin A + Sin B is not true for
A) A = 30°; B = 60°
B) A = 30°; B = 45°
C) A = 45°; B = 60°
D) A = 60°; B = 30°
Answer:
D) A = 60°; B = 30°

Question 117.
i) Sec θ = [latex]\frac{\text { Length of the hypotenuse }}{\text { Length of the side adjacent to } \theta}[/latex]
ii) Cot θ = [latex]\frac{\text { Length of the side opposite to } \theta}{\text { Length of the side adjacent to } \theta}[/latex]
A) (i), (ii) are true
B) (i), (ii) are false
C) (i) is false (ii) is true
D) (i) is true (ii) is false
Answer:
D) (i) is true (ii) is false

Question 118.
Ramu said Cos A = 2 ; Ravi said Cos A = 1. Do you agree with whom ?
A) Ramu
B) Ravi
C) Ramu and Ravi
D) Nobody
Answer:
B) Ravi

Question 119.
In ΔABC, ∠B = 90° then Sin A =
A) [latex]\frac{\mathrm{AC}}{\mathrm{AB}}[/latex]
B) [latex]\frac{\mathrm{AB}}{\mathrm{AC}}[/latex]
C) [latex]\frac{\mathrm{BC}}{\mathrm{AC}}[/latex]
D) [latex]\frac{\mathrm{BC}}{\mathrm{AB}}[/latex]
Answer:
C) [latex]\frac{\mathrm{BC}}{\mathrm{AC}}[/latex]

Question 120.
In a right angled triangle the adjacent side of 30°
A) Opposite side of 30°
B) Hypotenuse
C) Opposite side of 60°
D) Adjacent side of 60°
Answer:
C) Opposite side of 60°

Question 121.
Cos θ. Tan θ =
A) Sinθ
B) Cosθ
C) Cot θ
D) Sin² θ . Cos θ
Answer:
A) Sinθ

Question 122.
If Cos θ = [latex]\frac{a}{b}[/latex] then Cosec θ is equal to
A) [latex]\frac{\mathrm{b}}{\mathrm{a}}[/latex]
B) [latex]\frac{b}{\sqrt{b^{2}-a^{2}}}[/latex]
C) [latex]\frac{\sqrt{b^{2}-a^{2}}}{b}[/latex]
D) [latex]\frac{a}{\sqrt{b^{2}-a^{2}}}[/latex]
Answer:
B) [latex]\frac{b}{\sqrt{b^{2}-a^{2}}}[/latex]

Question 123.
Sec θ = [latex]\frac{\mathbf{m}+\mathbf{n}}{2 \sqrt{\mathbf{m n}}}[/latex] then Cosec θ =
A) [latex]\frac{\mathrm{mn}}{2}[/latex]
B) [latex]\frac{\mathrm{m}+\mathrm{n}}{2}[/latex]
C) [latex]\frac{m-n}{m+n}[/latex]
D) [latex]\frac{\mathrm{mn}}{\mathrm{m}+\mathrm{n}}[/latex]
Answer:
C) [latex]\frac{m-n}{m+n}[/latex]

Question 124.
Cos² θ (1 + Tan²θ) =
A) – Sin² θ
B) 1
C) Sin θ
D) – 1
Answer:
B) 1

Question 125.


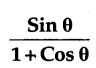
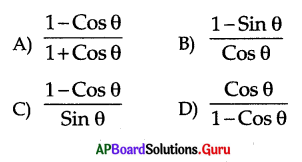
Answer:

Question 126.
Express Tan θ in terms of Sec θ.

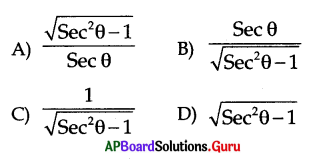
Answer:

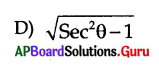
Question 127.
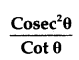– cotθ =
A) Cot θ
C) Sec θ
B) Cosec θ
D) Tan θ
Answer:
D) Tan θ

Question 128.
=
A) Cot θ
C) Sec θ
B) Tan θ
D) Cosec θ
Answer:
A) Cot θ

Question 129.
If cos θ = [latex]\frac{2 \sqrt{m n}}{m+n}[/latex] ,then sin θ =
A) [latex]\frac{m+n}{m-n}[/latex]
B) [latex]\frac{m-n}{m+n}[/latex]
C) [latex]\frac{2 \sqrt{\mathrm{mn}}}{\mathrm{m}+\mathrm{n}}[/latex]
D) [latex]\frac{\mathrm{m}+\mathrm{n}}{\mathrm{mn}}[/latex]
Answer:
B) [latex]\frac{m-n}{m+n}[/latex]

Question 130.
=
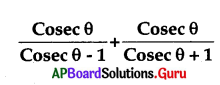A) 2 Sec θ
B) 2 Sec² θ
C) 2 Cosec θ
D) 2 Cosec² θ
Answer:
B) 2 Sec² θ

Question 131.
Sec θ (1 – Sin θ) (Sec θ + Tan θ) =
A) 0
B) 1
C) 2
D) -1
Answer:
B) 1

Question 132.
The ratio of lengths of opposite sides of 30°, 60°, 90° is
A) 1 : 2 : 3
B) 1 : 1 : √2
C) 1 : 3 : 2
D) 1 : √3 : 2
Answer:
D) 1 : √3 : 2

Question 133.
If Sin A = Cos B, then ……………………. (A, B are acute)
A) A = B
B) A + B = 180°
C) A = 90° + B
D) A + B = 90°
Answer:
D) A + B = 90°

Question 134.
=
A) – Tan² A
B) -Tan⁴ A
C) 1
D) – Sec² A
Answer:
B) -Tan⁴ A

Question 135.
If Tan θ + Sec θ = 8, then Sec θ – Tan θ value is
A) 8
B) [latex]\frac {1}{8}[/latex]
C) 6
D) 64
Answer:
B) [latex]\frac {1}{8}[/latex]

Question 136.
=
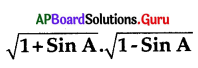A) Sin A
B) 1 – Sin²A
C) Cos A
D) 1
Answer:
C) Cos A

Question 137.
Sin θ = [latex]\frac{\mathrm{a}}{\mathrm{b}}[/latex]; Cos θ = [latex]\frac{\mathbf{c}}{\mathbf{d}}[/latex] then Cot θ =
A) [latex]\frac{a b}{c d}[/latex]
B) [latex]\frac{\mathrm{bc}}{\mathrm{ad}}[/latex]
C) [latex]\frac{c a}{b d}[/latex]
D) [latex]\frac{\mathrm{ad}}{\mathrm{bc}}[/latex]
Answer:
B) [latex]\frac{\mathrm{bc}}{\mathrm{ad}}[/latex]

Question 138.
Sin θ . Cot θ . Sec θ =
A) 2
B) -1
C) 1
D) 0
Answer:
C) 1

Question 139.
=
A) Sin θ
B) Cos θ
C) Tan θ
D) Cot θ
Answer:

Question 140.
Sin³ θ Cos θ + Cos³ θ Sin θ =
A) Sin θ + Cos θ
B) Sin θ Cos θ
C) Sin θ
D) Cot θ
Answer:
B) Sin θ Cos θ

Question 141.
Tan θ + Cot θ = 2, then Tan² θ + Cot² θ =
A) 4
B) 2
C) 6
D) 1
Answer:
B) 2

Question 142.
=
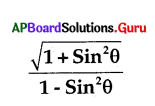A) Sec θ + Tan θ
B) Sec θ – Tan θ
C) Sec² θ + Tan² θ
D) Sec² θ – Tan² θ
Answer:
A) Sec θ + Tan θ

Question 143.
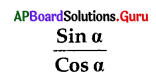. Cot α =
A) Tan α
C) 1
B) Cota
D) -1
Answer:
C) 1

Question 144.
If A, B and C are interior angles of a triangle ABC, then Sin ([latex]\frac{B+C}{2}[/latex]) =
A) Sin [latex]\frac{\mathrm{A}}{2}[/latex]
B) Cos [latex]\frac{\mathrm{A}}{2}[/latex]
C) – Sin [latex]\frac{\mathrm{A}}{2}[/latex]
D) – Cos [latex]\frac{\mathrm{A}}{2}[/latex]
Answer:
B) Cos [latex]\frac{\mathrm{A}}{2}[/latex]

Question 145.
can be expressed as …………….
A) Sin 0°
B) cos 90°
C) Sin 0° Cos 90°
D) Sin 60°
Answer:
D) Sin 60°

Question 146.
Cosec² A – Cot² A = 1 is true for all
A) 0° > A ≥ 90°
B) 0° < A ≥ 90° C) 0° > A < 90°
D) 0° < A ≤ 90°
Answer:
D) 0° < A ≤ 90°

Question 147.
From the adjacent figure ON = x; PN = y; OP = r ; ∠PON = θ and ∠PNO = 90° then
i) cos θ =

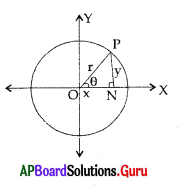
A) [latex]\frac{\mathrm{y}}{\mathrm{r}}[/latex]
B) [latex]\frac{\mathrm{y}}{\mathrm{x}}[/latex]
C) [latex]\frac{\mathrm{x}}{\mathrm{r}}[/latex]
D) [latex]\frac{\mathrm{r}}{\mathrm{x}}[/latex]
Answer:
C) [latex]\frac{\mathrm{x}}{\mathrm{r}}[/latex]

ii) Tan θ =
A) [latex]\frac{x}{y}[/latex]
B) [latex]\frac{\mathrm{y}}{\mathrm{x}}[/latex]
C) [latex]\frac{\mathrm{r}}{\mathrm{x}}[/latex]
D) [latex]\frac{\mathbf{r}}{\mathrm{y}}[/latex]
Answer:
B) [latex]\frac{\mathrm{y}}{\mathrm{x}}[/latex]

Question 148.
From the adjacent figure ΔABC, ∠B = 90°; ∠C = θ, then Sec θ =

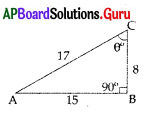
A) [latex]\frac{17}{15}[/latex]
B) [latex]\frac{17}{8}[/latex]
C) [latex]\frac{15}{17}[/latex]
D) [latex]\frac{15}{8}[/latex]
Answer:
A) [latex]\frac{17}{15}[/latex]

Question 149.
Which of the following represents Sin θ = [latex]\frac{21}{29}[/latex] ?

Answer:

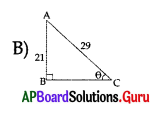
Question 150.
From the adjacent figure Sin C = [latex]\frac{3}{5}[/latex] then Cos A =

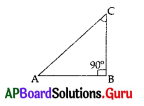
A) [latex]\frac{5}{4}[/latex]
B) [latex]\frac{5}{3}[/latex]
C) [latex]\frac{3}{5}[/latex]
D) [latex]\frac{4}{5}[/latex]
Answer:
C) [latex]\frac{3}{5}[/latex]

Question 151.
From this figure length of AB is
A) 20 √3 nits
B) [latex]\frac{20}{\sqrt{3}}[/latex] mts
C) 60 mts
D) 30 mts
Answer:
A) 20 √3 nits

Question 152.
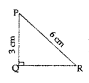From this figure ∠QPR =
A) 30°
B) 60°
C) 45°
D) 90°
Answer:
B) 60°

Question 153.
From the adjacent figure the length of the chord is

A) 3 cm
B) 4 cm
C) 6 cm
D) 12 cm
Answer:
C) 6 cm

Question 154.
From the adjacent figure length of Hypotenuse is

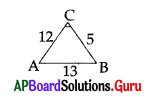
A) 5
B) 12
C) 13
D) 25
Answer:
C) 13

Question 155.
For finding ‘θ’ from the adjacent figure the trigonometric ratio used is

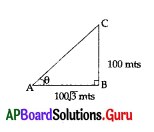
A) Sine
B) Cosine
C) Tangent
D) Cosecant
Answer:
C) Tangent