AP 10th Class Maths Bits 8th Lesson సరూప త్రిభుజాలు

Practice the AP 10th Class Maths Bits with Answers 8th Lesson సరూప త్రిభుజాలు on a regular basis so that you can attempt exams with utmost confidence.

AP Board 10th Class Maths Bits 8th Lesson సరూప త్రిభుజాలు

ప్రశ్న1.
∆ABCలో BC² + AB² = AC² అయిన……. లంబకోణమును కలిగిన శీర్షము.
A) A
B) B
C) C
D) నిర్ణయించలేము
జవాబు :
B) B

ప్రశ్న2.
∆ABCలో \(\frac{\mathbf{A D}}{\mathbf{D B}}=\frac{\mathbf{A E}}{\mathbf{E C}}\), D, Eలు AB, ACలపై బిందువులైన క్రింది వానిలో ఏది సత్యం ?
A) DE ∥ AB
B) DE ∥ AC
C) DE ∥ BC
D) DE ⊥ BC
జవాబు :
C) DE ∥ BC

ప్రశ్న3.
ఇచ్చిన పటంలో LM ∥ BC మరియు LN ∥ CD అయిన క్రింది వానిలో ఏది సత్యం ?

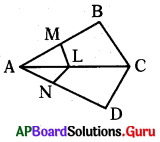
A) \(\frac{\mathrm{AM}}{\mathrm{MB}}=\frac{\mathrm{AL}}{\mathrm{LC}}\)
B) \(\frac{\mathrm{AN}}{\mathrm{ND}}=\frac{\mathrm{AL}}{\mathrm{LC}}\)
C) \(\frac{\mathrm{AM}}{\mathrm{MB}}=\frac{\mathrm{AN}}{\mathrm{ND}}\)
D) పైవి అన్నీ
జవాబు :
D) పైవి అన్నీ

ప్రశ్న4.
∆ABC ~ ∆DEF వాటి వైశాల్యాలు 64 సెం.మీ.² మరియు 121 సెం.మీ.² అయిన అనురూప భుజాల నిష్పత్తిని కనుగొనుము.
జవాబు :

∴ అనురూప భుజాల నిష్పత్తి = 8 : 11

ప్రశ్న5.
‘a’ భుజంగా గల క్రమ షడ్భుజ వైశాల్యము ఎంత ?
జవాబు :
‘a’ భుజంగా గల క్రమ షడ్భుజ వైశాల్యం
= 6 × \(\frac{\sqrt{3}}{4}\) a²

ప్రశ్న6.
ఒకడు తూర్పునకు 6 మీ., అచ్చట నుండి ఉత్తరమునకు 8 మీ. నడచిన ప్రారంభ స్థానము నుండి అతను ఎంత దూరంలో కలడు ?
జవాబు :
ప్రారంభం నుండి అతను గల దూరం AC.

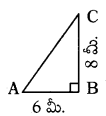
AC² = AB² + BC²
⇒ AC² = 6² + 8² = 100
⇒ AC = \(\sqrt{100}\) = 10 మీ.

ప్రశ్న7.
ఇచ్చిన పటంలో ∆BDA ~ ∆ADC అయితే ∠CAD విలువ ఎంత ?

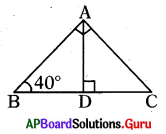
జవాబు :
∠CAD = 90°

ప్రశ్న8.
క్రింది వానిలో ఏవి లంబకోణ త్రిభుజ భుజాలకు ఉదాహరణ ?
A) 5, 6, 9
B) 5, 12, 13
C) 5, 11, 12
D) 7, 8, 9
జవాబు :
B) 5, 12, 13

ప్రశ్న9.
‘a’ భుజంగా గల సమబాహు త్రిభుజం ఎత్తును తెల్పండి.
జవాబు :
\(\frac{\sqrt{3}}{2}\) a

ప్రశ్న10.
∆ABC ~ ∆NYL, ∠C = 60°, ∠B = 70° అయిన ∠X విలువ ఎంత ?
జవాబు :
∠X = 50°

ప్రశ్న11.
ఇచ్చిన స్కేలు గుణకం ప్రకారం ఇచ్చిన త్రిభుజానికి సరూపంగా ఉండేటట్లు త్రిభుజాన్ని నిర్మించడానికి ఆధారంగా ఉపయోగపడేది
A) భు.భు.భు. సరూపత
B) కో.కో.కో. సరూపత
C) థమిక అనుపాత సిద్ధాంతం
D) A మరియు C
జవాబు :
D) A మరియు C

ప్రశ్న12.
∆ABC ~ ∆EDC అయిన, కింద సూచించ పటాలలో సరైన పటం …….

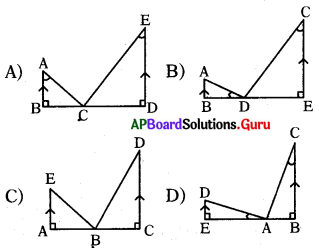
జవాబు :

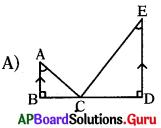
ప్రశ్న13.
∆ABC నందు ∠C = 90°, BC = a, CA = b AB = c మరియు ‘p’ అనునది ‘C’ నుండి AB పైకి గీచిన లంబం పొడవు అయిన క్రింది వానిలో ఏది సత్యం?

జవాబు :
C) \(\frac{1}{\mathrm{p}^{2}}=\frac{1}{\mathrm{a}^{2}}+\frac{1}{\mathrm{~b}^{2}}\)

ప్రశ్న14.
∆ABC లో AC = 12 సెం.మీ., AB = 5 సెం.మీ మరియు ∠BAC = 30° అయితే ∆ABC వైశాల్యమును కనుగొనుము.
జవాబు :

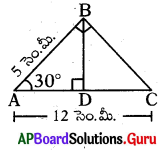
∆ADB లో ∠A = 30°
sin 30° = \(\frac{\mathrm{BD}}{\mathrm{AB}}\)
\(\frac{1}{2}=\frac{\mathrm{BD}}{5}\)
∴ BD = \(\frac{5}{2}\)
∴ ∆ABC వైశాల్యం = \(\frac{1}{2}\)bh
= \(\frac{1}{2}\) × AC × DB
5 = \(\frac{1}{2}\) × 12 × \(\frac{5}{2}\)
= 15 చ.సెం.మీ

ప్రశ్న15.
ఒక లంబకోణ త్రిభుజములోని భుజాలు పూర్ణాంకములు అయితే దానిలో కనీసము ఒక కొలత …………..
A) 3 యొక్క గుణిజము
B) 9 యొక్క గుణిజము
C) 2 యొక , గుణిజము
D) 7 యొక్క గుణిజము
జవాబు :
C) 2 యొక , గుణిజము

ప్రశ్న16.
క్రింది పటంలో ‘x’ విలువను a, bమరియు C పదాలలో తెల్పండి.

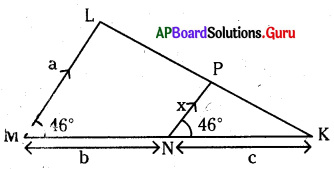
A) x = \(\frac{\mathrm{ac}}{\mathrm{b}+\mathrm{c}}\)
B) x = \(\frac{\mathrm{bc}}{\mathrm{b}+\mathrm{c}}\)
C) x = \(\frac{b+c}{a c}\)
D) x = \(\frac{\mathrm{ab}}{\mathrm{a}+\mathrm{c}}\)
జవాబు :
A) x = \(\frac{\mathrm{ac}}{\mathrm{b}+\mathrm{c}}\)

∆LMK- ∆PNK
∴\(\frac{\mathrm{LM}}{\mathrm{PN}}=\frac{\mathrm{MK}}{\mathrm{NK}} \Rightarrow \frac{\mathrm{a}}{\mathrm{x}}=\frac{\mathrm{b}+\mathrm{c}}{\mathrm{c}}\)
= x(b + c) = ac
∴ x = \(\frac{a c}{b+c}\)

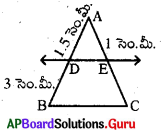
ప్రశ్న17.
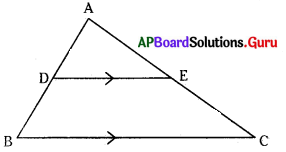
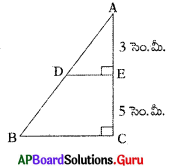
ఇచ్చిన పటంలో ∆ABC, DE ∥BC, AD = 1.5 సెం.మీ., DB = 6 సెం.మీ., AE = x సెం.మీ., EC = 8 సెం.మీ. అయిన x విలువ ఎంత ?

జవాబు :
\(\frac{\mathrm{AD}}{\mathrm{DB}}=\frac{\mathrm{AE}}{\mathrm{EC}} \Rightarrow \frac{1.5}{6}=\frac{\mathrm{AE}}{8}\)
⇒ AE = \(\frac{1.5 \times 8}{6}\) = 2 సెం.మీ

ప్రశ్న18.
∆ABC ~ ∆DEF మరియు వైశాల్యము (∆ABC) వైశాల్యము (∆DEF) = 49 : 100 అయిన DE : AB ని కనుగొనుము.
జవాబు :
DE : AB = \(\sqrt{100}\) : \(\sqrt{49}\) = 10 : 7

ప్రశ్న19.
‘x’ సెం.మీ. భుజముగా గల సమబాహు – త్రిభుజ ఉన్నతి ……. ,సెం.మీ.²
A) \(\frac{\sqrt{3}}{2}\)x
B) \(\frac{2}{\sqrt{3}}\)x
C) \(\frac{\sqrt{3}}{4}\)x²
D) \(\frac{\sqrt{3}}{2}\)x²
జవాబు :
A) \(\frac{\sqrt{3}}{2}\)

ప్రశ్న20.
క్రింది పటము నుండి ADE వైశాల్యము : ABC వైశాల్యముని కనుగొనుము.

జవాబు :
∆AED ~ ∆ACB
∴ ∆ADE వైశాల్యము : ∆ABC వైశాల్యము
AE² : AC² = 9 : 64.

ప్రశ్న21.
∆ABC లో E మరియు Fలు వరుసగా AB మరియు AC భుజాలపై గల బిందువులు. AE = 2 సెం.మీ., EB = 2.5 సెం.మీ., AF = 4 సెం.మీ., FC = 5 సెం.మీ., అయిన …….
A) EF ⊥ BC:
B) EF ⊥ AB
C) EF ∥ BC
D) EF ∥ AB
జవాబు :
C) EF ∥ BC

ప్రశ్న22.
క్రింది పటము నుండి ‘x’ విలువ ఎంత ? ,

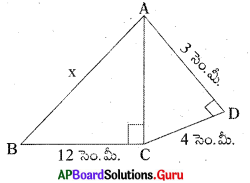
జవాబు :
AC = 5 సెం.మీ. [3, 4, 5; 5, 12, 13 పైథాగరియన్ త్రికాలు]
∴ AB = x = 13 సెం.మీ.

ప్రశ్న23.
రెండు సరూప త్రిభుజాల వైశాల్యాలు 100 చ. సెంమీ., 164 చ.సెం.మీ. వాటిలో పెద్ద త్రిభుజ మధ్యగతం పొడవు 10 సెం.మీ. అయితే చిన్న త్రిభుజ మధ్యగతం పొడవు ఎంత ?
జవాబు :
\(\frac{100}{64}=\left(\frac{M_{1}}{M_{2}}\right)^{2}=\left(\frac{10}{M_{2}}\right)^{2}\)
⇒ \(\left(\frac{10}{8}\right)^{2}=\left(\frac{10}{\mathrm{M}_{2}}\right)^{2}\) ⇒ M₂ = 8
చిన్న త్రిభుజ మధ్యగతం = 8 సెం.మీ.

ప్రశ్న24.
∆POR ~ ∆XYZ మరియు ∠X = 30°, ∠Q = 50°, అయిన ∠Z విలువ ఎంత ?
జవాబు :
∠P = ∠X = 30°, ∠Q = ∠Y = 50°,
∠R = ∠Z = ?
∴ ∠Z = 180 – (50 + 30) = 100°

ప్రశ్న25.
ఇచ్చిన పటం నుండి x విలువను కనుగొనుము.

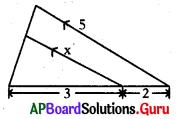
జవాబు :
\(\frac{x}{3}=\frac{5}{5}\) ⇒ x = 3

ప్రశ్న26.
∆ABC ~ ∆PQR మరియు ∠A + ∠B = 115°, అయిన ∠R విలువ ఎంత ?
జవాబు :
∠R = 65°

ప్రశ్న27.
∆ABC లో DE ∥ BC, AD = 2 సెం.మీ., DE = 3 సెం.మీ. మరియు AB = 6 సెం.మీ. అయిన BC భుజం పొడవు ఎంత ?
జవాబు :

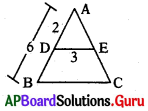
ADE ~ ABC
\(\frac{\mathrm{AD}}{\mathrm{AB}}=\frac{\mathrm{DE}}{\mathrm{BC}}\)
\(\frac{2}{6}=\frac{3}{\mathrm{BC}}\)
⇒ BC = 9 సెం.మీ.

ప్రశ్న28.
పటంలో ∠BDE విలువ కనుగొనుము.

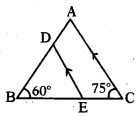
జవాబు :
∠B = 60°, ∠E = ∠C = 75°
∠BDE = ∠BAC = 180 – (60+ 75) = 45°

ప్రశ్న29.
క్రింది వానిలో త్రిభుజ వైశాల్యమును కనుగొను సూత్రము
A) A = \(\frac{1}{2}\) bh
B) A = \(\sqrt{(s-a)(s-b)(s-c)}\)
C) A = \(\sqrt{s(s-a)(s-b)(s-c)}\)
D) A మరియు C
జవాబు :
D) A మరియు C

ప్రశ్న30.
రెండు సరూప త్రిభుజాల వైశాల్యాల నిష్పత్తి 144:441 అయిన వాటి చుట్టుకొలతల నిష్పత్తి ఎంత?
జవాబు :
\(\sqrt{144}: \sqrt{441}\) = 12 : 21 = 4:7

ప్రశ్న31.
క్రింది ఇచ్చిన వాక్యా లలో సరియైనది. ”
A) అన్ని అల్పకోణ త్రిభుజాలు సరూపాలు.
B) అన్ని అధికకోణ త్రిభుజాలు సరూపాలు.
C) అన్ని లంబకోణ త్రిభుజాలు సరూపాలు.
D) అన్ని సమద్విబాహు లంబకోణ త్రిభుజాలు సరూపాలు.
జవాబు :
D) అన్ని సమద్విబాహు లంబకోణ త్రిభుజాలు సరూపాలు.

→ క్రింది పటంలో ∠BAC = 90° మరియు AD ⊥ BC. పటాన్ని పరిశీలించి 32 మరియు 33 ప్రశ్నలకు సమాధానాలు రాయండి.

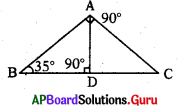
ప్రశ్న32.
∠DAC విలువ ఎంత ?
జవాబు :
∠DAC = 180 – (90 + 35) = 55°

ప్రశ్న33.
క్రింది వానిలో ఏది సత్యం ?
A) BC² = AB² + AC²
B) AD² = BD · DC
C) ∆ADB ~ ∆CDA .
D) పైవన్నీ
జవాబు :
D) పైవన్నీ

ప్రశ్న34.
క్రింది పటంలో ∠A = 90°, BD = 5, AD = 5√3 , మరియు DC = x అయిన x విలువను కనుగొనుము.

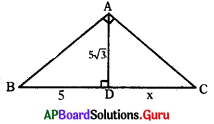
జవాబు :
AD² = BD . DC
(5√5)² = 5x ⇒ x = \(\frac{25 \times 3}{5}\) = 15

ప్రశ్న35.
∆ABC ~ ∆DEF, BC = 4 సెం.మీ, EF = 5 సెం.మీ మరియు ∆ABC వైశాల్యం 80 సెం.మీ2 అయిన ∆DEF వైశాల్యం ఎంత ?
జవాబు :

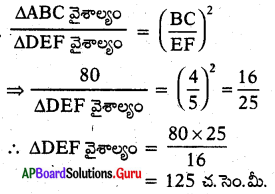
ప్రశ్న36.
ప్రవచనం-A : సరూప త్రిభుజాలు అన్ని సర్వసమాన త్రిభుజాలు అవుతాయి.
ప్రవచనం-B : అన్ని లంబకోణ సమద్విబాహు త్రిభుజాలు సరూపాలు.
A) A సత్యం, B అసత్యం
B) A అసత్యం, B సత్యం
C) A, B లు రెండూ సత్యం
D) A, B లు రెండూ అసత్యం
జవాబు :
B) A అసత్యం , B సత్యం

ప్రశ్న37.
రెండు త్రిభుజాలు సరూపాలు కావడానికి అవసరమగు నియమాలు ఏవి ?
i) వాటి అనురూప కోణాలు సమానంగా, ఉండాలి.
ii) వాటి అనురూప భుజాలు ఒకే నిష్పత్తిలో ఉండాలి.
A). పై రెండు నియమాలను పాటించాలి.
B) పై వానిలో ఏదో ఒక నియమాన్ని పాటిస్తే సరిపోతుంది.
C) పై రెండు నియమాలు సరిపోవు.
D) రెండు త్రిభుజాలు ఎప్పుడూ సరూపాలు కావు.
జవాబు :
B) పై వానిలో ఏదో ఒక నియమాన్ని పాటిస్తే సరిపోతుంది.

ప్రశ్న38.
∆ABC లో DE ∥ BC మరియు AD : DB = 1 : 2, అయిన ∆ADE : ∆ABC ని రాయండి.
జవాబు :

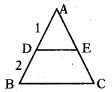
∆ADE : ∆ABC
= AD² : AB²
= 1² : 3²
= 1:9

ప్రశ్న39.
∆ABC ~ ∆PQR. BC మధ్య బిందువు M మరియు QR మధ్యబిందువు N. ∆ABC = 100 సెం.మీ2. ∆POR = 144 సెం.మీ² మరియు AM = 4 సెం.మీ అయిన PN విలువను కనుగొనుము.
జవాబు :

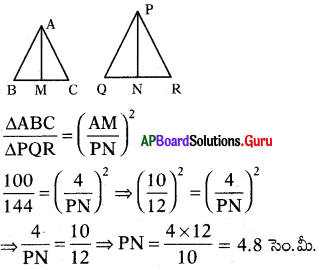
ప్రశ్న40.
భు.కో. భు. నియమాన్ని తెల్పండి.
జవాబు :
ఒక త్రిభుజములోని ఒక కోణము, వేరొక త్రిభుజము లోని ఒక కోణము సమానమై, ఈ కోణాలను కలిగివున్న భుజాలు అనుపాతంలో ఉంటే ఆ రెండు త్రిభుజాలు సరూపాలు.

ప్రశ్న41.
∆PQR లో PQ = 6√3 సెం.మీ., PR = 12 సెం.మీ. మరియు QR = 6 సెం.మీ. అయిన ∠Q కొలతను కనుగొనుము.
జవాబు :
PR² = 122 = 144 – PQ2 = (63)2 = 108,
QR2 = 62 = 36 – ‘PQ2 + QR2 = 108 – 36 = 144 = PR2
∴ ∠Q = 90° (పైథాగరస్ సిద్ధాంత విపర్యయము) .

ప్రశ్న42.
రాంబలోని కర్ణాలు 24 సెం.మీ మరియు 32 సెం.మీ అయిన రాంబస్ చుట్టుకొలతను సెం.మీ.లలో తెల్పండి.
జవాబు :

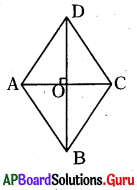
ABCD రాంబస్ కర్ణాలు AC = 24 సెం.మీ.,
BD = 32 సెం.మీ.
OA = 12 సెం.మీ., OD = 16 సెం.మీ.
∴ AD² = AO² + OD²
= 12² + 16²
= 144 + 256 = 400
AD = \(\sqrt{400}\) = 20
రాంబస్ చుట్టుకొలత = 4 x 20 = 80 సెం.మీ.
(లేదా)
AC² + BD² = 4 AB²
⇒ (24)² + (32)² = 4AB²
⇒ 4 AB² = 576 + 1024 = 1600
⇒ AB² = \(\frac{1600}{4}\) = 400 ⇒ AB = 20
రాంబస్ చుట్టుకొలత = 4 × 20 = 80 సెం.మీ.

ప్రశ్న43.
క్రింది వానిలో ఏవి లంబకోణ త్రిభుజ భుజాలు కావు ?
A) 9, 15, 12
B) 9, 5, 7
C) 400, 300, 500
D) 2, √5, 1
జవాబు :
B) 9, 5, 7

ప్రశ్న44.
సమద్విబాహు త్రిభుజం PORలో PR = QR మరియు PQ² = 2PR², అయిన 4R విలువ ఎంత ?
జవాబు :
∠R = 90°

ప్రశ్న45.
∆ABC లో AB, BC మరియు CA భుజాల మధ్య 2, బిందువులు వరుసగా D, E మరియు F లు అయిన ∆DEF : ∆ABC ని తెల్పండి.
జవాబు :
1 : 4

ప్రశ్న46.
స్కేలు గుణకము k విలువకు పటాల రూపానికి జతపరుచుము.

i) k >1	a) పెద్దవి చేయబడ్డ సరూప పటాలు
ii) k<1	b) సర్వసమాన పటాలు
iii) k = 1	c) చిన్నవి చేయబడ్డ సరూప పటాలు

A) i-a, ii-b, iii-c
B) i-b, ii-a, iii-c
C) i-a, ii-c, iii-b
D) i-b, ii-c, iii-a
జవాబు :
C) i-a, ii-c, iii-b

ప్రశ్న47.
రెండు సరూప త్రిభుజాల వైశాల్యాలు 25 మీ². మరియు 36 మీ². చిన్న త్రిభుజము మధ్యగతము 10 మీ. అయిన పెద్ద త్రిభుజ మధ్యగతం విలువ ఎంత ?
జవాబు :

ప్రశ్న48.
“రెండు సరూప త్రిభుజాల వైశాల్యాలు సమానం అయిన అవి సర్వసమానాలు”. (సత్యం/అసత్యం)
జవాబు :
సత్యం

ప్రశ్న49.
∆ABC మరియు ∆BDE లు రెండు సమబాహు త్రిభుజాలు, ‘D’, BC పై మధ్య బిందువు అయిన ∆ABC మరియు ∆BDE త్రిభుజ వైశాల్యాల నిష్పత్తి ఎంత ?
జవాబు :

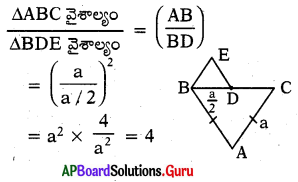
∴ ∆ABC : ∆BDE = 4 : 1

ప్రశ్న50.

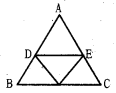
∆ABC లోని భుజాల మధ్య బిందువులను కలుపగా ఏర్పడిన నాలుగు త్రిభుజాలు ఎల్లప్పుడూ
A) సమబాహు త్రిభుజాలు
B) సమద్విబాహు త్రిభుజాలు
C) ∆ABC కి సర్వసమానాలు
D) ∆ABC కి సరూపాలు
జవాబు :
D) ∆ABC కి సరూపాలు

ప్రశ్న51.
“రెండు త్రిభుజాలలో ఒక త్రిభుజములోని భుజాలకు వేరొక త్రిభుజంలోని భుజాలు అనుపాతంలో ఉన్న ఆ త్రిభుజాలు సరూపాలు” అనునది ఏ సరూపకత నియమము ?
జవాబు :
భు.భు.భు. నియమం

ప్రశ్న52.
∆ABC ~ ∆XYZ; ∠C = 60°, ∠B = 75° అయిన ∠Z విలువ ఎంత ?
జవాబు :
∠C = ∠Z = 60°

ప్రశ్న53.
రెండు సరూప త్రిభుజాల వైశాల్యాలు 36 సెం.మీ మరియు 64 సెం.మీ2. మొదటి త్రిభుజపు ఒక భుజం 6 సెం.మీ అయిన రెండవ త్రిభుజంలోని అనురూప భుజం కొలత ఎంత ?
జవాబు :

∴ x = 8 సెం.మీ.

ప్రశ్న54.
పటంలో D, E లు AB మరియు AC ల మధ్య బిందువులు అయిన ∆ADE : ▢BCED ఎంత? ”

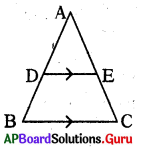
1 : 3

ప్రశ్న55.
∆PQR లంబకోణ త్రిభుజ భుజాలు PQ మరియు PRలు అయిన PQ = 5 సెం.మీ., PR = 13 సెం.మీ., ∠Q = 90° అయిన QR విలువ ఎంత ?
జవాబు :

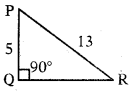
PR² = PQ² + OR²
13² – 5² = QR²
144 = QR²
∴ QR = 144 = 12 సెం.మీ.
(లేదా)
5, 12, 13 పైథాగరియన్ త్రికాలు
∴ QR = 12 సెం.మీ.

ప్రశ్న56.
క్రింది పటంలో D, Eలు AB మరియు ACల మధ్య బిందువులు. DE = 4 సెం.మీ అయిన BC కొలతను కనుగొనుము..

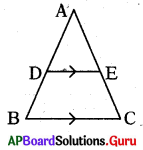
జవాబు :
BC = 2DE = 2 × 4 = 8 సెం.మీ.

ప్రశ్న57.
‘a’ యూనిట్లు భుజంగా గల సమబాహు త్రిభుజం వైశాల్యం ఎంత ?
జవాబు :
\(\frac{\sqrt{3}}{4}\)a² చ.యూనిట్లు

ప్రశ్న58.
∆ABC లో DE, AB మరియు AC లను 1:3 నిష్పత్తిలో విభజించిన BC = 4.8 సెం.మీ. అయిన DEని కనుగొనుము.

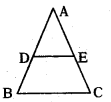
జవాబు :
AB, AC లను DE ఒకే నిష్పత్తి 1 : 3లో విభజిస్తున్నది.
DE ∥BC, BC = 4.8
∆ADE ~ ∆ABC
\(\frac{\mathrm{DE}}{\mathrm{BC}}=\frac{\mathrm{AD}}{\mathrm{AB}} \Rightarrow \frac{\mathrm{DE}}{4.8}=\frac{1}{4}\)
⇒ DE = \(\frac{1}{4}\) × 4.8 = 1.2 సెం.మీ.

ప్రశ్న59.
క్రింది పటంలో AB = 2.5 సెం.మీ, AC = 3.5 సెం.మీ, AD, BAC యొక్క కోణ సమద్విఖండనరేఖ అయిన BD: DC = ……

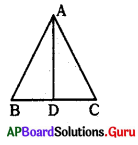
A) 5:3
B) 3:5
C) 5:7
D) 2:7
జవాబు :
C (కోణసమద్విఖండన రేఖ ఎదుటి భుజాన్ని మిగిలిన రెండు భుజాల నిష్పత్తిలో విభజిస్తుంది. 2.5 : 3.5 = 5:7]

ప్రశ్న60.
ఒక చతురస్ర కర్ణము 7√2 సెం.మీ అయిన ఆ చతురస్ర వైశాల్యం ఎంత ?
జవాబు :
చతురస్ర కర్ణం d = √2s = 7√2
∴ భుజం s = 7 సెం.మీ.
∴ చతురస్ర వైశాల్యం = 7² = 49 చ.సెం.మీ.

ప్రశ్న61.
పటంలో ∠BAD = ∠CAD; AB = 3.4 సెం.మీ, BD = 4 సెం.మీ, BC = 10 సెం.మీ అయిన AC విలువను కనుగొనుము.

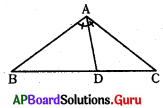
జవాబు :
\(\frac{\mathrm{AB}}{\mathrm{AC}}=\frac{\mathrm{BD}}{\mathrm{DC}} \Rightarrow \frac{3.4}{\mathrm{AC}}=\frac{4}{6}\) ⇒ AC = \(\frac{3.4 \times 6}{4}\)
= 5.1 సెం.మీ.

ప్రశ్న62.
రెండు సరూప త్రిభుజ భుజాల నిష్పత్తి 1 : 2 అయిన వాటి వైశాల్యా ల నిష్పత్తి ఎంత ?
జవాబు :
వైశాల్యా ల నిష్పత్తి = 7² : 2² = 49 : 4

ప్రశ్న63.
∆ABC ~ ∆POR; ∠A = 32°, ∠R = 650 అయిన ∠B విలువ ఎంత ?
జవాబు :
∠A = ∠P = 32°, ∠C = ∠R = 65°
∴ ∠B = ∠Q = 83°

ప్రశ్న64.
∆POR ~ ∆ABC అయిన y + 2 ఎంత?

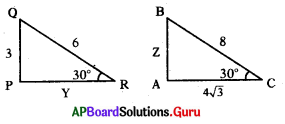
జవాబు :

Y + Z = 4 + 3√3

ప్రశ్న65.
పై 64వ ప్రశ్నలో త్రిభుజాల యొక్క స్కేలు గుణకం k విలువ ఎంత?
జవాబు :
స్కేలు గుణకం k = \(\frac{\mathrm{AB}}{\mathrm{PQ}}=\frac{\mathrm{BC}}{\mathrm{QR}}=\frac{\mathrm{AC}}{\mathrm{QR}}\)
= \(\frac{8}{6}=\frac{4}{3}\)

ప్రశ్న66.
∆ABC ~ ∆LMN అయిన వాటి చుట్టుకొలతలు 60 సెం.మీ. మరియు 48.సెం.మీ., LM = 8 సెం.మీ. అయిన AB విలువను కనుగొనుము.
A) 12
B) 15
C) 8
D) 10
జవాబు :
D, \(\frac{60}{48}=\frac{\mathrm{AB}}{\mathrm{LM}} \Rightarrow \frac{60}{48}=\frac{\mathrm{AB}}{8}\)
⇒ AB = \(\frac{60 \times 8}{48}\) = 10 సెం.మీ.

ప్రశ్న67.
∆ABC ~ ∆PQR మరియు ..
\(\frac{\mathbf{A B}}{\mathbf{P Q}}=\frac{\mathbf{B C}}{\mathbf{Q R}}=\frac{\mathbf{A C}}{\mathbf{P R}}\) = k; k 1 అయిన
A) ∆ABC కన్నా ∆PCR పెద్ద పటము.
B) ∆ABC కన్నా ∆POR చిన్న పటము.
C) ∆ABC, ∆POR లు సర్వసమాన పటాలు.
D) పైవి అన్నీ సాధ్యము
జవాబు :
B) ∆ABC కన్నా ∆POR చిన్న పటము.

ప్రశ్న68.
∆ABC = ∆XYZ, \(\frac{\mathbf{A B}}{\mathbf{X Y}}=\frac{\mathbf{B C}}{\mathbf{Y Z}}=\frac{\mathbf{A C}}{\mathbf{X Z}}\) = k అయిన
A) k = 1
B) k > 1
C) k < 1
D) నిర్ణయించలేము
జవాబు :
A) k = 1

ప్రశ్న69.
∆ABC లో DE// BC మరియు D, Eలు వరుసగా AB, AC లపై బిందువులైన క్రింది వానిలో ఏది సత్యం ?
A) \(\frac{\mathrm{AD}}{\mathrm{DB}}=\frac{\mathrm{AE}}{\mathrm{EC}}\)
B) \(\frac{\mathrm{AD}}{\mathrm{AB}}=\frac{\mathrm{AE}}{\mathrm{EC}}\)
C) \(\frac{\mathrm{BC}}{\mathrm{AB}}=\frac{\mathrm{AC}}{\mathrm{BC}}\)
D) \(\frac{\mathrm{AD}}{\mathrm{EC}}=\frac{\mathrm{AE}}{\mathrm{DB}}\)
జవాబు :
A) \(\frac{\mathrm{AD}}{\mathrm{DB}}=\frac{\mathrm{AE}}{\mathrm{EC}}\)

ప్రశ్న70.
∆PQR లో EF ∥ QR, E, Fలు PQ, PRలపై బిందువులు. మరియు PE = 4 సెం.మీ.,
QE = 4.5 సెం.మీ., PF = 8 సెం.మీ. అయిన RF విలువను కనుగొనుము.
జవాబు :

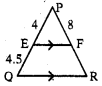
\(\frac{\mathrm{PE}}{\mathrm{EQ}}=\frac{\mathrm{PF}}{\mathrm{FR}} \Rightarrow \frac{4}{4.5}=\frac{8}{\mathrm{RF}}\)
∴ RF = \(\frac{8 \times 4.5}{4}\) = 9 సెం.మీ.

ప్రశ్న71.
క్రింది పటంలో DE ∥ BC అయిన AC విలువను లెక్కించండి.

జవాబు :

ప్రశ్న72.
క్రింది పటంలో DE ∥ BC మరియు BD = 7.2 సెం.మీ., AC = 7.2 సెం.మీ., EC = 5.4 సెం.మీ. అయిన AD విలువ ఎంత ?

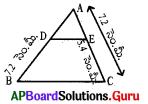
జవాబు :

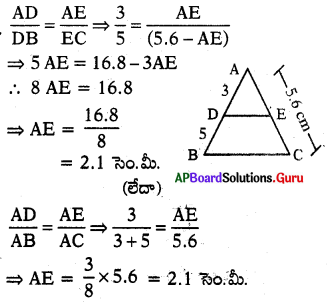
ప్రశ్న73.
∆ABC లో DE ∥ BC మరియు \(\frac{\mathrm{AD}}{\mathrm{DB}}=\frac{3}{5}\) AC = 5.6 సెం.మీ. అయిన AE విలువను కనుగొనుము.
జవాబు :

ప్రశ్న74.
ఇచ్చిన పటంలో ∆ABC ~ ∆EDC అయిన AB = 1.6 సెంమీ., CD = 15 సెం.మీ., BC = 1.5 సెం.మీ. అయిన x విలువ ఎంత ?

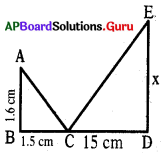
జవాబు :
\(\frac{\mathrm{AB}}{\mathrm{ED}}=\frac{\mathrm{BC}}{\mathrm{CD}} \Rightarrow \frac{1.6}{\mathrm{x}}=\frac{1.5}{15}\) ⇒ x = 16 సెం.మీ.

ప్రశ్న75.
4 మీ. పొడవు గల ఒక జెండా స్తంభము 6 మీ. పొడవు గల నీడను ఏర్పరిచిన సమయంలో 24 మీ. ఎత్తు గల భవనం ఏర్పరిచే నీడ పొడవు ఎంత ?
జవాబు :
\(\frac{4}{6}=\frac{24}{x}\) (24 మీ. ఎత్తుగల భవనం నీడ పొడవు = x మీ.)
:. భవనం నీడ పొడవు x = 24 × \(\frac{6}{4}\) = 36 మీ.

ప్రశ్న76.
క్రింది వానిలో ఏది అసత్యం ?
A) రెండు సరూప త్రిభుజాల వైశాల్యాలు సమానమైన అవి సర్వసమాన త్రిభుజాలు.
B) రెండు త్రిభుజాలలో, ఒక త్రిభుజంలోని భుజాలు వేరొక త్రిభుజంలోని భుజాలకు అనుపాతంలో ఉన్న ఆ రెండు త్రిభుజాలలోని అనురూప కోణాలు సమానము.
C) ఒక త్రిభుజములోని ఏవైనా రెండు భుజాలను ఒకే నిష్పత్తిలో విభజించు సరళరేఖ మూడవ భుజానికి లంబము.
D) ఒక త్రిభుజంలో ఒక భుజానికి సమాంతరంగా గీచిన రేఖ మిగిలిన రెండు భుజాలను ఒకే నిష్పత్తిలో విభజిస్తుంది.
జవాబు :
C) ఒక త్రిభుజములోని ఏవైనా రెండు భుజాలను ఒకే నిష్పత్తిలో విభజించు సరళరేఖ మూడవ భుజానికి లంబము.

ప్రశ్న77.
రెండు సరూప త్రిభుజాల చుట్టుకొలతలు వరుసగా 40 సెం.మీ., 28 సెం.మీ. మొదటి త్రిభుజంలోని ఒక భుజం కొలత 10 సెం.మీ. అయిన రెండవ త్రిభుజంలోని అనురూప భుజం కొలత ఎంత ?
\(\frac{40}{28}=\frac{10}{x}\) ⇒ x = 10 × \(\frac{28}{40}\) ⇒ x = 7 సెం.మీ.
∴ రెండవ త్రిభుజ అనురూప భుజం = 7 సెం.మీ.

ప్రశ్న78.
∆PORలో PQ, QRల మధ్యబిందువులు M, N లు మరియు PR = x సెం.మీ., MN = y సెం.మీ. అయిన x, y ల మధ్య సంబంధమును రాయండి.

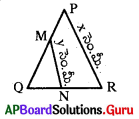
జవాబు :
x = 2y

ప్రశ్న79.
క్రింది పటంలో ∆ARB – ∆SRT మరియు RA = 6 సెం.మీ., AS = 2 సెం.మీ., AB = 9 సెం.మీ. అయిన ST విలువ ఎంత ?

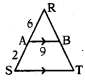
జవాబు :
∆ARB – ∆SRT ⇒ \(\frac{\mathrm{AR}}{\mathrm{SR}}=\frac{\mathrm{AB}}{\mathrm{ST}}\)
⇒ \(\frac{6}{8}=\frac{9}{\mathrm{ST}}\) ⇒ ST = 9 × \(\frac{8}{6}=\frac{72}{6}\) = 12 సెం.మీ.

ప్రశ్న80.
క్రింది పటంలో AB ∥DE మరియు AB = 24 సెం.మీ., DE = 12 సెం.మీ., BC = 22 సెం.మీ. అయిన CD ని కనుగొనుము.

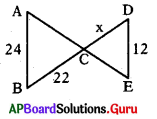
జవాబు :
∆ABC ~ ∆EDC
∴ \(\frac{\mathrm{AB}}{\mathrm{ED}}=\frac{\mathrm{BC}}{\mathrm{DC}} \Rightarrow \frac{24}{12}=\frac{22}{\mathrm{DC}}\) ⇒ 2 = \(\)
∴ DC = \(\frac{22}{2}\) = 11 సెం.మీ.

ప్రశ్న81.
క్రింది ఇవ్వబడిన లంబకోణ త్రిభుజాలలో ∠PQR = ∠LTS అయిన x విలువ ఎంత ?

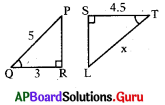
జవాబు :
∆PRQ ~ ∆LST
⇒ \(\frac{\mathrm{PQ}}{\mathrm{LT}}=\frac{\mathrm{QR}}{\mathrm{TS}} \Rightarrow \frac{5}{\mathrm{x}}=\frac{3}{4.5}\)
⇒ 3x = 5 × 4.5
⇒ x = \(\frac{5 \times 4.5}{3}\) = 7.5 సెం.మీ.

ప్రశ్న82.
∆ABC ~ ∆DEF, వాని వైశాల్యాలు వరుసగా 64 చ.సెం.మీ., 121 చ.సెం.మీ. మరియు EF = 15.4 సెం.మీ. అయిన AB విలువను కనుగొనుము.
జవాబు :
\(\frac{\Delta \mathrm{ABC}}{\Delta \mathrm{DEF}}=\left(\frac{\mathrm{AB}}{\mathrm{DE}}\right)^{2}=\left(\frac{\mathrm{BC}}{\mathrm{EF}}\right)^{2}=\left(\frac{\mathrm{AC}}{\mathrm{DF}}\right)^{2}\)
∆DEF లోని EF భుజానికి BC అనురూప భుజం అవుతుంది. కావున AB విలువను కనుగొనలేము.

ప్రశ్న83.
ప్రాథమిక అనుపాత సిద్ధాంతాన్ని నిర్వచించుము.
జవాబు :
ప్రాథమిక అనుపాత సిద్ధాంతము (వేల్స్ సిద్ధాంతము):

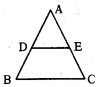
ఒక త్రిభుజంలో ఒక భుజానికి సమాంతరంగా గీసిన రేఖ మిగిలిన రెండు భుజాలను వేరు వేరు బిందువులలో ఖండించిన, ఆ మిగిలిన రెండు భుజాలు ఒకే నిష్పత్తిలో విభజింపబడతాయి.
∆ABC లో DE ∥ BC అయిన \(\frac{\mathrm{AD}}{\mathrm{DB}}=\frac{\mathrm{AE}}{\mathrm{EC}}\)
దీనినే ‘థేల్స్’ సిద్ధాంతము (లేక) ప్రాథమిక అనుపాత సిద్ధాంతము అంటారు.

ప్రశ్న84.
క్రింది వానిలో ఏవి లంబకోణ త్రిభుజ భుజాల కొలతలు ?
i) 3, 4, 5
ii) 7, 12, 15
iii) 3, 6, 8
iv) 13, 12, 5
A) i, ii
B) i, ii, iii
C) i, iv
D) i, iii, iv
జవాబు :
C) i, iv

ప్రశ్న85.
ఒక లంబకోణ త్రిభుజంలో AB = 3 సెం.మీ., BC = 4 సెం.మీ., AC = 5 సెం.మీ. అయిన లంబకోణాన్ని కలిగిన శీర్షము ఏది ?
జవాబు :
AC² = AB² + BC² కావున లంబకోణం కలిగిన శీర్షం = B.

ప్రశ్న86.
ABCD ట్రెపీజియంలో AB ∥ DC మరియు కర్ణాలు AC, BDలు ‘O’ బిందువు వద్ద ఖండించుకొంటే
A) \(\frac{\mathrm{OA}}{\mathrm{OC}}=\frac{\mathrm{OB}}{\mathrm{OD}}\)
B) \(\frac{\mathrm{AC}}{\mathrm{BD}}=\frac{\mathrm{AB}}{\mathrm{DC}}\)
C) \(\frac{\mathrm{OA}}{\mathrm{OC}}=\frac{\mathrm{OD}}{\mathrm{OB}}\)
D) \(\frac{\mathrm{AC}}{\mathrm{BD}}=\frac{\mathrm{DC}}{\mathrm{AB}}\)
జవాబు :
A) \(\frac{\mathrm{OA}}{\mathrm{OC}}=\frac{\mathrm{OB}}{\mathrm{OD}}\)

ప్రశ్న87.
PQ² = PR² + QR² అయ్యేటట్లు ∆PQR భుజాలను కలిగి ఉంటే ఆ త్రిభుజము
A) ∆POR లంబకోణ త్రిభుజము మరియు ∠P = 90.
B) ∆PQR అధికకోణ త్రిభుజము మరియు ∠R అధిక కోణము.
C) ∆PQR లంబకోణ త్రిభుజము మరియు ∠R = 90°.
D) ∆POR అధికకోణ త్రిభుజము మరియు ∠P అధిక కోణము.
జవాబు :
C) ∆PQR లంబకోణ త్రిభుజము మరియు ∠R = 90°.

ప్రశ్న88.
ప్రాథమిక అనుపాత సిద్ధాంత విపర్యయాన్ని రాయుము.
జవాబు :

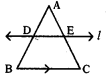
ఒక త్రిభుజములో ఏవైనా రెండు భుజాలను ఒకే నిష్పత్తిలో విభజించు సరళరేఖ, మూడవ భుజానికి సమాంతరంగా ఉండును.
∆ABCలో, \(\frac{\mathrm{AD}}{\mathrm{DB}}=\frac{\mathrm{AE}}{\mathrm{EC}}\) అయిన l ∥ BC అగును. దీనినే ‘థేల్స్ సిద్ధాంతపు విపర్యయము’ లేదా ‘ప్రాథమిక సిద్ధాంతపు విపర్యయము’ అంటారు.

ప్రశ్న89.
ట్రెపీజియం ABCD లో AB ∥ DC, E మరియు F లు వరుసగా EF ∥ AB అగునట్లు AD, BCలపై నున్న బిందువులైన క్రింది వానిలో ఏది సత్యం?
(లేదా)
క్రింది పటంలో AB ∥ DC మరియు EF ∥ AB అయ్యేటట్లు ABCD ఒక ట్రెపీజియం అయిన క్రింది వానిలో ఏది సత్యం ?

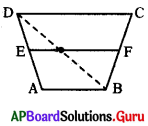
A) \(\frac{\mathrm{AB}}{\mathrm{DC}}=\frac{\mathrm{AD}}{\mathrm{BC}}\)
B) \(\frac{\mathrm{AE}}{\mathrm{ED}}=\frac{\mathrm{CF}}{\mathrm{FB}}\)
C) \(\frac{\mathrm{AE}}{\mathrm{ED}}=\frac{\mathrm{BF}}{\mathrm{FC}}\)
D) \(\frac{\mathrm{DE}}{\mathrm{EA}}=\frac{\mathrm{BF}}{\mathrm{FC}}\)
జవాబు :
C) \(\frac{\mathrm{AE}}{\mathrm{ED}}=\frac{\mathrm{BF}}{\mathrm{FC}}\)

ప్రశ్న90.
ABCD ట్రెపీజియంలో AB ∥ DC, మరియు కర్ణాలు AC, BD లు ‘O’ వద్ద ఖండించుకొంటే ∆AOB మరియు ∆COD కు సంబంధించి క్రింది దేనితో నీవు ఏకీభవిస్తావు ?
(లేదా)
ఇచ్చిన పటంలో ABCD ట్రెపీజియం , AB ∥ CD అయిన కింది వానిలో దేనితో నీవు ఏకీభవిస్తావు ?

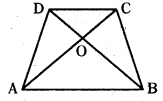
A) ∆AOB ~ ∆COD
B) ∆AOB వైశాల్యం = ∆COD వైశాల్యం
C) ∆AOB ≅ ∆COD
D) ∆AOB, ∠COD లు లంబకోణ త్రిభుజాలు
జవాబు :
A) ∆AOB ~ ∆COD

ప్రశ్న91.
ఒక వ్యక్తి 24 మీ. పడమర వైపు ప్రయాణించిన తరువాత 10 మీ. దక్షిణం వైపు ప్రయాణించాడు. అతను బయలు దేరిన స్థానం నుండి ఎంత దూరంలో కలడు ?
జవాబు :

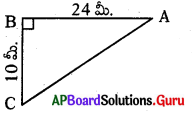
(బయలుదేరిన స్థానం A నుండి ప్రస్తుతం గల స్థానం Cకి గల దూరం)
AC² = AB² + BC²
⇒ AC² = 24² + 10² = 576 + 100
∴ AC = \(\sqrt{676}\)= 26 సెం.మీ.

ప్రశ్న92.
12 సెం.మీ., 5 సెం.మీ. లు ఆసన్న భుజాలుగా గల దీర్ఘ చతురస్ర కర్ణము పొడవును కనుగొనుము.
జవాబు :
దీర్ఘచతురస్ర కర్ణం పొడవు = \(\sqrt{l^{2}+b^{2}}\)
= \(\sqrt{12^{2}+5^{2}}=\sqrt{169}\) = 13 సెం.మీ.

ప్రశ్న93.
క్రింది పటంలో ABCD దీర్ఘ చతురస్రము మరియు AB = l మీ., BC = b మీ., AC = d మీ. అయిన d ను l, b లలో తెల్పండి.

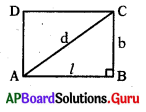
జవాబు :
d² = l² + b²
⇒ d = \(\sqrt{l^{2}+b^{2}}\)

ప్రశ్న94.
ఉదయం 9 గంటల సమయంలో 18 మీ. పొడవు గల చెట్టు 9 మీ. పొడవు గల నీడను ఏర్పరచిన, అదే సమయ 40 మీ. ఎత్తుగల సెల్ టవరు నీడ పొడవు ఎంత?
జవాబు :
\(\frac{18}{9}=\frac{40}{x}\) (x సెల్ టవరు నీడ పొడవు)
2 = \(\frac{40}{x}\) ⇒ x = \(\frac{40}{2}\) = 20

ప్రశ్న95.
క్రింది పటంలో ∠ACB = ∠AED = 90° మరియు ∠ADE= ABC అయిన క్రింది వానిలో ఏది సత్యం ?

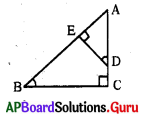
A) ∆ABC ~ ∆DEA
B) ∆ABC ~ ∆ADE
C) ∆ABC ~ ∆EDA
D) ∆ABC ~ ∆AED
జవాబు :
B) ∆ABC ~ ∆ADE

ప్రశ్న96.
క్రింది పటంలో ∆ABC లో ∠B = 90° మరియు BD I AC అయిన క్రింది వానిలో ఏది సత్యం ?

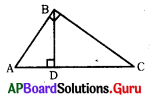
A) ∆ADB ~ ∆ABC
B) ∆BDC ~ ∆ABC
C) ∆ADB ~ ∆BDC .
D) పైవన్నీ
జవాబు :
D) పైవన్నీ

ప్రశ్న97.
12 మీ. పొడవు గల విద్యుత్ స్తంభానికి 20 మీ. పొడవు గల ఒక తీగ కట్టబడినది. తీగ యొక్క రెండవ చివరను ఒక మేకుకు కట్టి, భూమిపై స్తంభం నుండి ఎంత దూరంలో ఆ మేకును పాతిన తీగ బిగుతుగా నుండును ?
జవాబు :
తీగ బిగుతుగా ఉండుటకు స్తంభం నుండి మేకును నాటు దూరము = BC

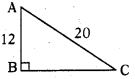
⇒ AC² = AB² + BC²
⇒ 20² = 12² + BC²
⇒ 400 – 144 = BC²
⇒ 256 = BC² = BC = 16 మీ.

ప్రశ్న98.
ఒక వ్యక్తి x మీటర్ల దూరం తూర్పు వైపునకు ప్రయాణించి తరువాత 5 మీటర్లు ఉత్తరంవైపు ప్రయాణించాడు. ప్రస్తుతం అతను ప్రారంభ స్థానం. నుండి 4 మీటర్ల దూరంలో కలడు.
పై సమాచారాన్ని పటంలో చూపండి.
జవాబు :

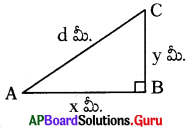
ప్రశ్న99.
పై 98వ ప్రశ్నలో ‘d’ విలువను x, y లలో తెల్పండి.
జవాబు :
d² = x² + y²
d = \(\sqrt{x^{2}+y^{2}}\)

ప్రశ్న100.
∆ABC మరియు ∆XYZ లలో \(\frac{\mathrm{AB}}{\mathrm{XY}}=\frac{\mathrm{BC}}{\mathrm{YZ}}=\frac{\mathrm{AC}}{\mathrm{XZ}}=\frac{3}{5}\) అయిన ∆ABC వైశాల్యము ∆XYZ వైశాల్యంలో ఎంత శాతము ?
జవాబు :

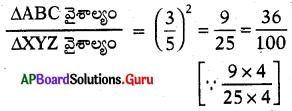
∴ ∆ABC వైశాల్యం ∆XYZ వైశాల్యంలో 36% ఉంటుంది.

ప్రశ్న101.
క్రింది పటంలో PQ ∥ RS అయిన క్రింది వానిలో దేనిని నీవు సత్యంగా అంగీకరిస్తావు ?

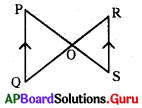
A) ∆POQ ~ ∆SOR
B) ∆POQ = ∆SOR
C) ∠POQ = 2∠SOR
D) పైవన్నీ
జవాబు :
A) ∆POQ ~ ∆SOR

ప్రశ్న102.
∆ABC లో ∠B = 90° అయిన AC² = AB² + BC² అనునది
A) ప్రాథమిక అనుపాత సిద్ధాంతము
B) పైథాగరస్ సిద్ధాంతము
C) పైథాగరస్ సిద్ధాంత విపర్యయము
D) లం.క.భు. నియమము
జవాబు :
B) పైథాగరస్ సిద్ధాంతము

ప్రశ్న103.
క్రింది వానిలో ఏది అసత్యం ?
A) ఒక లంబకోణ త్రిభుజము మూడు కొలతలు పూర్ణసంఖ్యలైనపుడు కనీసము ఒకటి తప్పనిసరిగా సరిసంఖ్య అవుతుంది.
B) ఒక లంబకోణ త్రిభుజంలో కర్ణం మీది వర్గము మిగిలిన రెండు భుజాల మీది వర్గాల మొత్తానికి సమానము.
C) ∆PQR లో PQ² = PR² + RQ² అయిన R = 90°
D) ఒక లంబకోణ త్రిభుజం ABC లో ∠B =90° అయిన ∠A, ∠C లు సంపూరక కోణాలు.
జవాబు :
D) ఒక లంబకోణ త్రిభుజం ABC లో ∠B =90° అయిన ∠A, ∠C లు సంపూరక కోణాలు.

ప్రశ్న104.
రెండు సరూప త్రిభుజ వైశాల్యాల నిష్పత్తి a:9 అయిన , వాని భుజాల నిష్పత్తి ఎంత ?
జవాబు :
భుజాల నిష్పత్తి = √a : 3.

ప్రశ్న105.
∆ABC ~ ∆POR మరియు AB² = PQ, QR = 4, BC = 1 అయిన AB విలువను కనుగొనుము.
జవాబు :
\(\frac{\mathrm{AB}}{\mathrm{PQ}}=\frac{\mathrm{BC}}{\mathrm{QR}} \Rightarrow \frac{\mathrm{AB}}{\mathrm{AB}^{2}}=\frac{1}{4} \Rightarrow \frac{1}{\mathrm{AB}}=\frac{1}{4}\)
∴ AB = 4.

ప్రశ్న106.
క్రింది పటంలో DE ∥ BC అయిన CE =

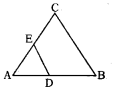
A) AD.AE
B) \(\frac{\text { AD.EA }}{\text { DB }}\)
C) \(\frac{\text { DB.EA }}{\text { AD }}\)
D) ఏదీకాదు
జవాబు :
C) \(\frac{\text { DB.EA }}{\text { AD }}\)

ప్రశ్న107.
క్రింది పటంలో చూపినట్లు X, Y, Zలు QR, PR, PQల యొక్క మధ్యబిందువులు. మరియు ∆XYR వైశాల్యము 8 సెం.మీ² అయిన పై పటం నందు షేడ్ చేయని ప్రాంత వైశాల్యము ఎంత ?

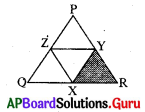
జవాబు :
\(\frac{8}{4}\) = 2 సెం.మీ²

ప్రశ్న108.

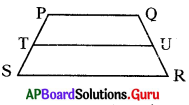
పై ట్రెపీజియం నందు PQ ∥ RS ∥ TU అయిన PT. UR = ………..
A) PT.TS
B) PT.QU
C) TS.DU
D) TS.UR
జవాబు :
C) TS.DU

ప్రశ్న109.
∆POR – ∆STU, ∠P = 30° అయిన ∠Q + ∠U విలువ ఎంత ?
జవాబు :
∠Q + ∠U = 180° – 30° = 150°

ప్రశ్న110.
PORS ట్రెపీజియం నందు PR, QS లపై గల ఉమ్మడి బిందువు ‘T’ మరియు PT = 20, QT = 4, RT = 5 అయిన ST = ……. సెం.మీ.
జవాబు :

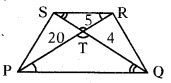
పై ట్రెపీజియం PORS లో
∆PTQ ~ ∆RTS

ప్రశ్న111.
4.2 సెం.మీ. పొడవుగల రేఖాఖండాన్ని 5 : 2 నిష్పత్తిలో విభజించు బిందువు వల్ల ఏర్పడే రెండు రేఖాఖండాల పొడవుల భేదం = ………… సెం.మీ.
జవాబు :
\(\frac{4.2}{7}\) × (5 – 2) = 1.8 సెం.మీ.

ప్రశ్న112.
ఈ క్రింది వానిలో క్రమ బహుభుజి కానిది …..
A) సమబాహు త్రిభుజం
B) చతురస్రం
C) రాంబస్
D) పైవన్నీ
జవాబు :
C) రాంబస్

ప్రశ్న113.
సమద్విబాహు త్రిభుజం ఒక క్రమ బహుభుజి కాదు. ఎందుకనగా ………
A) దానియందలి అన్ని కోణాలు సమానం కాదు
B) దాని యందలి భుజాలన్నీ సమానం కాదు.
C) దానికి ఒక స్థిరమైన ఆకారం లేదు.
D) ‘A’ మరియు ‘B’ రెండూ
జవాబు :
D) ‘A’ మరియు ‘B’ రెండూ

ప్రశ్న114.
పైథాగరస్ సిద్ధాంత విపర్యయమును రాయుము.
జవాబు :
ఒక త్రిభుజములో ఒక భుజము మీది వర్గము మిగిలిన రెండు భుజాల వర్గాల మొత్తానికి సమానమైన, మొదటి భుజానికి ఎదురుగా ఉండే కోణము లంబకోణము అనగా త్రిభుజము లంబకోణ త్రిభుజమవుతుంది.

ప్రశ్న115.
∠P = 60°, ∠R = 60° మరియు ∆ABC ~ ∆PQR అయిన ఈ క్రింది వాటిలో సత్యమేది ?
A) ∠B = 60°
B) ∆ABC సమబాహు త్రిభుజం
C) ∠A = 60°
D) పైవన్నీ
జవాబు :
D) పైవన్నీ

ప్రశ్న116.
∆ABC ~ ∆POR మరియు AB = 4 సెం.మీ., BC = 5 సెం.మీ., AC = 6 సెం.మీ., PQ = 12 సెం.మీ. అయిన ∆POR చుట్టుకొలత ఎంత?
జవాబు :

⇒ ∆PQR చుట్టుకొలత = 15 × 3 = 45 సెం.మీ.

ప్రశ్న117.

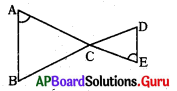
‘పై పటంలో ∠A = ∠E అయిన పటంలోని సరూప త్రిభుజాలను గుర్తునుపయోగించి సూచించండి.
జవాబు :
∆ABC ~ ∆EDC (లేదా)
∆BAC ~ ∆DEC (లేదా)
∆CAB ~ ∆CED …..

ప్రశ్న118.
రెండు సరూప త్రిభుజ వైశాల్యాల నిష్పత్తి 8 : 8 అయిన అవి ఎల్లప్పుడూ ………… త్రిభుజాలు.
A) సమబాహు
B) లంబకోణ
C) సర్వసమాన
D)సర్వసమాన సమబాహు
జవాబు :
C) సర్వసమాన

ప్రశ్న119.
∆ ABC నందు ∠B = 90°, భుజాల పొడవులన్నీ పూర్ణాంకాలే అయితే,
A) కనీసం ఒక బేసి సంఖ్య ఉండును.
B) కనీసం ఒక సరి సంఖ్య ఉండును.
C) కనీసం రెండు సరి సంఖ్యలు ఉండును.
D) కనీసం రెండు బేసి సంఖ్యలు ఉండును.
జవాబు :
B) కనీసం ఒక సరి సంఖ్య ఉండును.

→ “∆ABCలో ∠A = ∠B అయిన BC = AC”. – పై ప్రవచనం ఆధారంగా 120, 121 ప్రశ్నలకు సమాధానాలు రాయండి.

ప్రశ్న120.
పై ప్రవచనం యొక్క వ్యతిరేక ప్రవచనం రాయండి.
జవాబు :
∆ABC లో ∠A ≠ ∠B అయిన BC ≠ AC
(లేదా)
∆ABC లో ∠A = ∠B కానిచో BC = AC కాదు

ప్రశ్న121.
పై ప్రవచనం యొక్క విపర్యయమును రాయండి.
జవాబు :
∆ABC లో BC = AC అయిన ∠A = ∠B.

ప్రశ్న122.
క్రింది ABCD దీర్ఘచతురస్రం నందు (OA + OB) (OA – OB) విలువ క్రింది వానిలో దేనికి సమానము ?

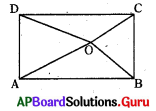
A) OD²
B) OC²
C) OD² + OC²
D) OD² – OC²
జవాబు :
D) OD² – OC²

OA² + 0C² = OD² + OB²
⇒ OA² – OB² = OD² – OC²
⇒ (OA + OB) (OA – OB) = OD² – OC²

ప్రశ్న123.
∆ABC, ∆DEF లలో AB = DE, BC = EF మరియు AC = DF అయిన క్రింది వానిలో ఏది సత్యం ?
A) ∠A = ∠D
B) ∆ABC: ∆DEF
C) ∆ABC వైశాల్యం = ∆DEF వైశాల్యం
D) పైవన్నీ
జవాబు :
D) పైవన్నీ

ప్రశ్న124.
ఇచ్చిన పటంలో DE ∥ BC, AD : DB = 3:2, DE = 10 సెం.మీ.

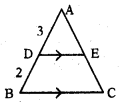
క్రింది వానిని జతపరుచుము.

i) AE : EC	a) 3 : 5
ii) AE : AC	b) 9 : 25
iii) ∆ADE వైశాల్యం : ∆ABC వైశాల్యం	c) 3 : 2
iv) EC : AC	d) 2 : 5

A) i-c, ii-a, iii-b, iv-d
B) i-a, ii-b, iii-d, iv-c
C) i-c, ii-b, iii-d, iv-a
D) i-c, ii-d, iii-b, iv-a
జవాబు :
A) i-c, ii-a, iii-b, iv-d

ప్రశ్న125.
వివిధ సందర్భాలలో మనం గణితంలో ఉపయోగించే గుర్తులను ఆయా సందర్భాలకు జతపరుచుము.

i) =	a) సరూపాలు
ii) ~	b) సర్వసమానాలు
iii) ⇒	c) అయినచో
iv) ∥	d) సమాంతరాలు

A) i-b, ii-c, iii-a, iv-d
B) i-b, ii-d, iii-c, iv-a
C) i-a, ii-c, iii-d, iv-b
D) i-b, ii-a, iii-c, iv-d
జవాబు :
D) i-b, ii-a, iii-c, iv-d

ప్రశ్న126.
రెండు సరూప త్రిభుజాల వైశాల్యాల నిష్పత్తి 3 : 5 అయిన వాటి చుట్టుకొలతల నిష్పత్తిని రాయండి.
జవాబు :
√3 : √5.

ప్రశ్న127.
రెండు సరూప త్రిభుజాల చుట్టుకొలతల నిష్పత్తి 4 : 9 అయిన వాటి వైశాల్యాల నిష్పత్తి ఎంత ?
జవాబు :
2 : 3

ప్రశ్న128.
రెండు సరూప త్రిభుజాల చుట్టుకొలతల నిష్పత్తి 25 : 16 అయిన వాటి అనురూప భుజాల నిష్పత్తి ఎంత ?
జవాబు :
25 : 16

ప్రశ్న129.
క్రింది పటం నందు ∆POR ~ ∆TSR అయిన APOR చుట్టుకొలతను కనుగొనుము.

జవాబు :

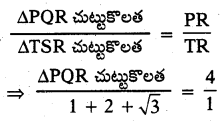
= ∆PQR చుట్టుకొలత = 4(3 + √3)
= 12 + 4√5 సెం.మీ.

ప్రశ్న130.
\(\frac{\sqrt{3}}{2}\) యూనిట్లు భుజంగా గల సమబాహు త్రిభుజంతో √3 స్కేలు గుణకంగా గల సరూప త్రిభుజ వైశాల్యంను కనుగొనుము.
జవాబు :
\(\frac{\sqrt{3}}{2}\) భుజంగా గల సమబాహు త్రిభుజ వైశాల్యం

(లేదా)
\(\frac{\sqrt{3}}{2}\) యూనిట్లు భుజంగా గల సమబాహు త్రిభుజంతో
√3 స్కేలు గుణకంగా గల సరూప త్రిభుజ భుజం
= √3\(\left(\frac{\sqrt{3}}{2}\right)=\frac{3}{2}\)

∴ \(\frac{3}{2}\) యూనిట్లు భుజంగా గల సమబాహు త్రిభుజ

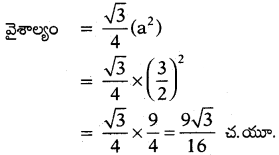
ప్రశ్న131.
చతురస్ర కర్ణం 8 సెం.మీ. అయిన దాని చుట్టుకొలత 16√2 చ.సెం.మీ. అని చూపండి.
జవాబు :
చతురస్ర కర్ణం d = 8 సెం.మీ. (చతురస్రంలో కర్ణం d = √2s)
√2 s = 8 ⇒ s = \(\frac{8}{\sqrt{2}}\)
చుట్టుకొలత = 4s = 4 × \(\frac{8}{\sqrt{2}}=\frac{32}{\sqrt{2}}=\frac{32 \times \sqrt{2}}{\sqrt{2} \times \sqrt{2}}\)
= 16√2 సెం.మీ.

ప్రశ్న132.
క్రింది పటాల సరూపకతను, వాని నియమాలకు జతపరుచుము.

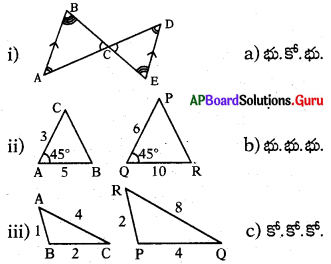
A) i-b, ii-a, iii-c
B) i-c, ii-b, iii-a
C) i-c, ii-a, iii-b
D) i-b, ii-c, iii-a’
జవాబు :
C) i-c, ii-a, iii-b

ప్రశ్న133.
∆ABC నందు (AB + BC) (AB – BC) = AC² అయిన క్రింది వానిలో ఏది సత్యం ?
A) ∠A = 90°
B) ∠B = 90°
C) ∠C = 90°
D) ఏదీకాదు
జవాబు :
C) ∠C = 90°

(AB + BC) (AB – BC) = AC²
∴ AB² – BC² = AC²
⇒ AB² = AC² + BC² (పైథాగరస్ సిద్ధాంత విపర్యయము)
∴ ∠C = 90°

ప్రశ్న134.
ఒక సమబాహు త్రిభుజం యొక్క వైశాల్యం √3 చ.యూ. అయిన దాని చుట్టుకొలత ఎంత ?
జవాబు :
సమబాహు త్రిభుజ వైశాల్యం \(\frac{\sqrt{3}}{4}\) a = √3
= a = √3 × \(\frac{4}{\sqrt{3}}\)
∴ a² = 4 ⇒ a = √4 = 2
చుట్టుకొలత = 3a = 3 × 2 = 6 యూనిట్లు,

ప్రశ్న135.
∆ABC – ∆POR, ∠A + ∠R= 135° అయిన ∠B + ∠Q విలువ ఎంత ?
జవాబు :
∆ABC ~ ∆POR, ∠A + ∠R = 135°
⇒ ∠A + ∠C = 135°
∴ ∠B = ∠Q = 180° – 135° = 45°
⇒ ∠B + ∠ = 90°

ప్రశ్న136.
క్రింద ఇవ్వబడిన సరూప త్రిభుజాలను, వాని గుర్తులను జతపరుచుము.

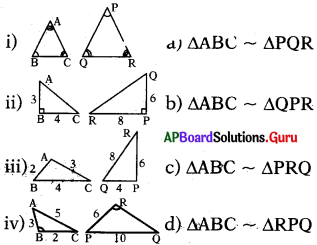
A) i-a, ii-b, iii-d, iv-c
B) i-d, ii-b, iii-a, iv-c
C) i-b, ii-a; iii-c, iv-d
D) i-c, ii-b, iii-a, iv-d
జవాబు :
B) i-d, ii-b, iii-a, iv-c

ప్రశ్న137.
90 సెం.మీ. ఎత్తు గల బాలిక దీపస్తంభము నుండి 1.2 మీ./సె. వేగంతో నడుస్తున్నది. దీపస్తంభం ఎత్తు 3.6.మీ. అయిన 4 సెకండ్ల తరువాత ఆ బాలిక పొడవు ఎంత ?
పై సమస్యా సాధనకు సరిపడు చిత్తుపటాన్ని గీయండి.
జవాబు :

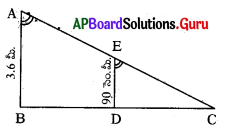
AB = దీపస్తంభము
DE = బాలిక

ప్రశ్న138.
q ⇒ p యొక్క విపర్యయమును గుర్తును ఉపయోగించి రాయండి.
జవాబు :
q ⇒ p యొక్క విపర్యయము p ⇒ q.

→ గమనిక : క్రింద ఇవ్వబడిన పటంలోని సమాచారాన్ని – ఉపయోగించుకొని 139-141 వరకు గల ప్రశ్నలకు సమాధానాలు రాయండి.

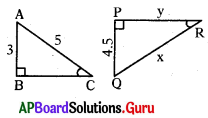
ప్రశ్న139.
పటంలోని త్రిభుజాల సరూపకతను గుర్తులను ఉపయోగించి రాయండి.
జవాబు :
∆ABC ~ ∆QPR

ప్రశ్న140.
x విలువ ఎంత ?
జవాబు :

ప్రశ్న141.
y విలువ ఎంత ?
జవాబు :
∆ABC లో (∵ 3, 4, 5 పైథాగరియన్ త్రికాలు)
∠B = 90°
∴BC = 4 యూనిట్లు
\(\frac{\mathrm{AB}}{\mathrm{QP}}=\frac{\mathrm{BC}}{\mathrm{PR}} \Rightarrow \frac{3}{4.5}=\frac{4}{\mathrm{PR}}\) ⇒ PR= \(\frac{4 \times 4.5}{3}\)
= 6 యూనిట్లు
(లేదా)
∆PQR లో PQ = 4.5, QR = 7.5, PR = ?, ∠P = 90°
QR² = PQ² + PR²
⇒ (7.5)² = (4.5)² + PR²
⇒ (7.5)² – (4.5)² = PR²
⇒ (7.5 + 4.5) (7.5 – 4.5) = PR²
⇒ 12 × 3 = PR²
⇒ PR² = 36 ⇒ PR = \(\sqrt{36}\) = 6 యూనిట్లు

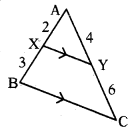
→ ఇచ్చిన పటం ఆధారంగా 142, -143 ప్రశ్నలకు సమాధానాలు రాయండి.

ప్రశ్న142.
పటంలోని రెండు త్రిభుజాలు.ఏ సరూపకతా నియమం – ప్రకారం.సరూపాలు ?
జవాబు :
కో.కో.కో నియమం (లేదా) కో.కో (లేదా) భు.కో. భు.

ప్రశ్న143.
రెండు త్రిభుజాల యొక్క సరూపకతను గుర్తును ఉపయోగించి రాయండి.
జవాబు :
∆AXY ~ ∆ABC

ప్రశ్న144.
సరూప పటాలకు ఒక ఉదాహరణనివ్వండి.
జవాబు :
రెండు వృత్తాలు (లేదా) రెండు చతురస్రాలు (లేదా) రెండు సర్వసమాన త్రిభుజాలు (లేదా) రెండు లంబకోణ సమద్విబాహు త్రిభుజాలు.

ప్రశ్న145.
సరూపంకాని పటాలకు ఒక ఉదాహరణనివ్వండి.
జవాబు :
ఒక త్రిభుజం, ఒక చతురస్రం (లేదా) వృత్తం, చతుర్భుజం.

ప్రశ్న146.
రాంబస్ ఒక క్రమబహుభుజి అని కౌశిక్ అంటున్నాడు. – కొశిక్ సమాధానాన్ని నీవు సమర్థిస్తావా! వ్యతిరేకిస్తావా ! ఎందుకు ?
జవాబు :
కౌశిక్ సమాధానాన్ని వ్యతిరేకిస్తాను. ఎందుకనగా రాంబస్లో నాలుగు భుజాలు సమానం, కాని నాలుగు కోణాలు సమానం కాదు. కావున రాంబస్ క్రమ బహుభుజి కాదు.

ప్రశ్న147.
“దీర్ఘ చతురస్రంలోని కోణాలన్నీ సమానాలు, కావున దీర్ఘచతురస్రం ఒక క్రమబహుభుజి అని ఆలం అంటున్నాడు. ఆలం వాదన సరైనదా ? కాదా ! ఎందుకు ?
జవాబు :
ఆలం వాదన సరైనది కాదు. ఎందుకనగా దీర్ఘ చతురస్రంలోని నాలుగు కోణాలు సమానం కాని నాలుగు భుజాలు సమానం కాదు. కావున దీర్ఘచతురస్రం క్రమ బహుభుజి కాదు.

ప్రశ్న148.
రెండు బహుభుజులు సరూపాలు కావడానికి అవసరమగు నియమాలు తెల్పండి.
జవాబు :
రెండు బహుభుజులు ‘సరూపం కావాలంటే

1. వాటి అనురూప కోణాలు సమానంగా ఉండాలి.
2. వాటి అనురూప భుజాలు ఒకే నిష్పత్తిలో ఉండాలి.

ప్రశ్న149.
i) అనురూప కోణాలు సమానం కావాలి.
ii) అనురూప భుజాల నిష్పత్తి సమానం కావాలి.’ రెండు త్రిభుజాలు సరూపాలు కావడానికి పై రెండు నియమాలలో ఏదోకటి సరిపోతుంది అని సురేష్ అంటు న్నారు. సురేష్ సమాధానంతో నీవు ఏకీభవిస్తావా ? లేదా ?
జవాబు :
సురేష్ సమాధానంతో ఏకీభవిస్తాను.

ప్రశ్న150.
రెండు సరూప త్రిభుజాల చుట్టుకొలతలు వరుసగా 24 సెం.మీ. మరియు 18 సెం.మీ. మొదటి త్రిభుజ ఒక భుజం 8 సెం.మీ. అయిన రెండవ త్రిభుజంలో అనురూప భుజం పొడవెంత?
జవాబు :
6

ప్రశ్న151.
∆ARC లో ∠B = 90° మరియు BD ⊥ AC. AD = 8 సెం.మీ., BD = 4 సెం.మీ. అయిన CD పొడవెంత?
జవాబు :
2√3 సెం.మీ.

ప్రశ్న152.
∆ARC మరియు ∆DEF లలో ∠B = ∠E, ∠C = 4, అయిన క్రింది ప్రవచనాలలో ఏది సత్యమైనది ?
A) \(\frac{\mathbf{A B}}{\mathbf{D E}}=\frac{\mathbf{C A}}{\mathbf{E F}}\)
B) \(\frac{\mathbf{B C}}{\mathbf{E F}}=\frac{\mathbf{A B}}{\mathbf{F D}}\)
C) \(\frac{\mathbf{A B}}{\mathbf{D E}}=\frac{\mathbf{B C}}{\mathbf{E F}}\)
D) \(\frac{\mathbf{C A}}{\mathbf{F D}}=\frac{\mathbf{A B}}{\mathbf{E F}}\)
జవాబు :
C) \(\frac{\mathbf{A B}}{\mathbf{D E}}=\frac{\mathbf{B C}}{\mathbf{E F}}\)

ప్రశ్న153.
క్రింది పటంలో DE ∥ BC, AD = 4.5 సెం.మీ., BD = 9 సెం.మీ., మరియు EC = 8 సెం.మీ., AE పొడవును కనుగొనండి.

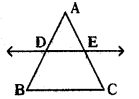
జవాబు :
AD = 4.5 సెం.మీ., BD = 9 సెం.మీ. EC = 8 సెం.మీ.
\(\frac{\mathrm{AD}}{\mathrm{DB}}=\frac{\mathrm{AE}}{\mathrm{EC}} \Rightarrow \frac{4.5}{9}=\frac{\mathrm{AE}}{8}\) ⇒ 9AE = 36
∴ AE = 4 సెం.మీ.

ప్రశ్న154.
“వృత్తాలు”, “చతురస్రాలు” మరియు “త్రిభుజాలు” వీటిలో ఏవి ఎల్లప్పుడూ సరూపాలు కానివి ఏవి ?
జవాబు :
త్రిభుజాలు.

ప్రశ్న155.
∆ABC, ∆DEF లు రెండు సమబాహు త్రిభుజ భుజాల పొడవులు వరుసగా 4 సెం.మీ. మరియు5 సెం.మీ. అయితే \(\frac{{ar}(\Delta D E F)}{{ar}(\Delta A B C)}\) ను కనుగొనుము.
జవాబు :
రెండు సరూప త్రిభుజాల వైశాల్యాల నిష్పత్తి, వాటి అనురూప భుజాల వర్గాల నిష్పత్తికి సమానము.
\(\frac{(\Delta \mathrm{DEF})}{(\Delta \mathrm{ABC})}=\frac{5^{2}}{4^{2}}=\frac{25}{16}\)

ప్రశ్న156.
∆ABC ~ ∆DEF మరియు ∠A = ∠D = 90%, అయితే ∠B + ∠F విలువ కనుగొనండి.
జవాబు :
∆ABC ~ ∆DEF
⇒ A = ∠D = 90°
∠B = ∠E; C = ∠F
∆ABC లో ∠A + ∠B + ∠C = 180°
∠A = ∠D = 90° ను తీసుకొనగా
⇒ 90° + B + C = 180°
⇒ ∠B + ∠C = 90°
∠C = ∠F గా తీసుకొనగా
⇒ ∠B + ∠F = 90°

ప్రశ్న157.
క్రింది పటంలో AB ∥ CD సరూప, త్రిభుజాల సమానత్వమును వ్రాయండి.

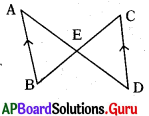
జవాబు :
∠AEB = ∠CED ( శీర్షాభిముఖ కోణాలు)
కో.కో.కో. సరూప నియమం ప్రకారం
∴ ∠BEA = ∠CDE లు సరూపాలు.
∆BEA ~ ∆CDE