AP 10th Class Maths Bits 6th Lesson శ్రేఢులు

Practice the AP 10th Class Maths Bits with Answers 6th Lesson శ్రేఢులు on a regular basis so that you can attempt exams with utmost confidence.

AP Board 10th Class Maths Bits 6th Lesson శ్రేఢులు

ప్రశ్న1.
1, -1, – 3, ……. A.P. యొక్క సామాన్య భేదంను రాయండి.
జవాబు :
సామాన్య భేదం d = a₂ – a₁ = 1 – 1 = -2

ప్రశ్న2.
0.6, 1.9, 3.2, ……… అంకశ్రేణి సామాన్యభేదంను కనుగొనండి.
జవాబు :
d = 1.9 – 0.6 = 1.3

ప్రశ్న3.
14, 11, 8, …. అంకశ్రేణిలో మొదటి ఋణ పదమును తెల్పండి.
జవాబు :
ఇచ్చిన అంకశ్రేణిని పొడిగించగా
14, 11, 8, 5, 2 – 1,…….
∴ మొదటి ఋణపదం = -1

ప్రశ్న4.
ఒక గుణ శ్రేణి నందు n వ పదం ar^n-1 అయిన r సూచించునది ………
A) సామాన్య భేదం
B) సామాన్య నిష్పత్తి
C) మొదటి పదం
D) వ్యాసార్ధం
జవాబు :
B

ప్రశ్న5.
ఒక A.P. లో n వ పదం a_n = 3 + 2n అయిన సామాన్య భేదం ఎంత ?
జవాబు :
a_n = 3 + 2n,
∴ a₁ = 3+ 2 = 5,
a₁ = 3 + 2(2) = 7
సామాన్య భేదం d = a₂ – a₁ = 7 – 5 = 2.
(Note: nవ పదంలో n గుణకమే సామాన్య భేదం అవుతుంది. ∴ d = 2)

ప్రశ్న6.
ఒక అంకశ్రేణి x – y,x, x + y, ….. యొక్క సామాన్య భేదంను కనుగొనుము.
జవాబు :
d = x – (x – y) = x – x + y =y.

ప్రశ్న7.
2a-b, 4a – 3b, 6a-5bశ్రేణి యందు సామాన్య భేదంను గణించండి.
జవాబు :
d = (4a – 3b) – (2a – b)
= 4a – 3b – 2a + b = 2a – 26

ప్రశ్న8.
ఒక గుణ శ్రేణి నందు మొదటి పదం 20 మరియు 4వ పదం 540 అయిన సామాన్య నిష్పత్తిని కనుగొనుము.
జవాబు :
గుణశ్రేణిలో a = 20,
4 వ పదం a₄ = ar³ = 540,

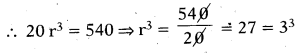
∴ r = 3

ప్రశ్న9.
అంకశ్రేఢి యొక్క ‘n’ పదాల మొత్తంనకు సూత్రాన్ని తెల్పండి.
జవాబు :
S_n = \(\frac{n}{2}\)[22 + (n – 1)d] (లేదా)
S_n = \(\frac{1}{2}\)[a + l]

ప్రశ్న10.
ఒక అంకశ్రేణి నందు 3వ పదం 5, 7వ పదం 9 అయిన ఆ శ్రేఢి సామాన్య భేదం ఎంత ?
జవాబు :

Short cut :
a₇ – a₃ ⇒ 4d = 9 – 5 = 4
∴ d = 1

ప్రశ్న11.
√2 సామాన్య నిష్పత్తి గల గుణశ్రేణినొక దానిని రాయండి.
జవాబు :
1, √2, 2, 2√2, ……….

ప్రశ్న12.
ఒక అంకశ్రేణిలో a₂₅ – a₁₂ =- 52 అయిన దాని సామాన్య భేదమును కనుగొనుము.
జవాబు :
a₂₅ – a₁₂ = (a + 24d) – (a + 11d) =-52
⇒ 240 – 11d = – 52
⇒ 13d = – 52
∴ d = \(\frac{-52}{13}\) = -4

ప్రశ్న13.
log 2 + log 4 + log 8 + log 16 + ….. శ్రేణిలోని పది పదముల మొత్తము
A) 45 log 2
B) 90 log 2
C) 10 log 2
D) 55 log 2
జవాబు :
log 2 + log 4 + log 8 + log 16 +… 10 పదాలు.
log 2¹ + log 2² + log 2³ + log 2⁴ + ….. + log 2¹⁰
= log 2 + 2 log 2 + 3 log 2 + 4 log 2 + ……. + 10 log 2
= [1 + 2 + 3 + 4 + ……. + 10] log 2
= 55 log 2
(లేదా)
log (2¹ × 2² × 2³ × …….. 2¹⁰)
= log 2^{1+ 2 + 3 + …… + 10}
= log2⁵⁵ = 55 log 2

ప్రశ్న14.
24, 21, 18, ….. అంకశ్రేణిలో ఋణపదము అయ్యే మొదటి పదము ఏది ?
జవాబు :
ఇచ్చిన అంకశ్రేడిని కొనసాగించగా
24, 21, 18, 15, 12, 9, 6, 3, 0, – 3, ……
మొదటి ఋణ పదం a₁₀ = -3

ప్రశ్న15.
మొదటి 100 సహజ సంఖ్యల మొత్తంను కనుగొనుము.
A) 4050
B)4500
C) 5500
D) 5050
జవాబు :
D మొదటి n సహజ సంఖ్యల మొత్తం = \(\frac{\mathrm{n}(\mathrm{n}+1)}{2}\)
n = 100, మొదటి 100 సహజ సంఖ్యల మొత్తం
\(\frac{100 \times 101}{2}\) = 50 × 101 = 5050

ప్రశ్న16.
a, b, cలు గుణశ్రేణిలో ఉంటే be a, Cలలో తెల్పండి.
జవాబు :
a, b, c లు A.P. లో ఉంటే b – a = c – b
⇒ 2b = a + c ⇒ b = \(\frac{a+c}{2}\)

ప్రశ్న17.
గుణశ్రేణి 3, .3√3 , 9, ……… లో ఎన్నవ పదం 243 అగును ?
జవాబు :
3, 3√3, 9, …………
a = 3, r = \(\frac{a_{2}}{a_{1}}=\frac{3 \sqrt{3}}{3}\) = √3, a_n = 243
a 3 G.P లో a_n = a.r^n-1 = 243
3(√3)^n-1 = 243
= (√3)^n-1 = \(\frac{243}{3}\) = 81
⇒ 3^n-1/2 = 3⁴ ⇒ \(\frac{\mathrm{n}-1}{2}\) = 4 ⇒ n – 1 = 8
∴ n = 9
9వ పదం 243 అవుతుంది.
(లేదా)
ఇచ్చిన G.P పొడిగించగా
3, 3√3, 9, 9√3, 27, 27√3, 81, 81√3, 243, ……
9వ పదం 243 అవుతుంది.

ప్రశ్న18.
x, x + 2, x + 6 లు గుణశ్రేణిలో మూడు వరుస పదాలైన ‘X’ విలువను కనుగొనుము.
జవాబు :
x, x + 2, x + 6 లు G.Pలో మూడు వరుస పదాలు అయిన
\(\frac{a_{2}}{a_{1}}=\frac{a_{3}}{a_{2}} \Rightarrow \frac{x+2}{x}=\frac{x+6}{x+2}\)
(x + 2)² = x(x + 6)

⇒ 4 = 6x – 4x ⇒ 4 = 2x ⇒ x = \(\frac{4}{2}\) = 2

ప్రశ్న19.
ఒక అంకశ్రేణిలో మొదటి రెండు పదాలు వరుసగా -3 మరియు 4 అయితే 21 వ పదంను కనుగొనుము.
జవాబు :
మొదటి పదం a₁ = a = -3,
రెండవ పదం a₂ = 4
∴ d = a₂ – a₁ = 4 – (- 3) = 7.
21వ పదం a_n = a + 20 d
=-3 + 20 (7) = 137

ప్రశ్న20.
ఒక అంకశ్రేణిలో a₁₈ – a₁₄ = 32 అయితే సామాన్య భేదం ఎంత ?
జవాబు :
a₁₈ – a₁₄ = 32 ⇒ 4d = 32
d = \(\frac{32}{4}\) = 8

ప్రశ్న21.
ఒక అంకశ్రేణిలో a = 1, a_n = 20 మరియు S_n = 399 అయిన n విలువను కనుగొనుము.
జవాబు :
a = 1, a_n = 1 = 20, S_n = 399
S_n = \(\frac{n}{2}\) [a + l] = 399
⇒ \(\frac{n}{2}\)[1 + 20] = 399
⇒ n(21) = 399 × 2
⇒ \(\frac{399 \times 2}{21}\) = 19 × 2 = 38

ప్రశ్న22.
\(\frac{1}{3}, \frac{1}{9}, \frac{1}{27}\) ……. అనే గుణశ్రేణిలో వన్నవ పదం \(\frac{1}{2187}\) అవుతుంది ?
జవాబు :

(లేదా)
\(\frac{1}{3}, \frac{1}{9}, \frac{1}{27}, \frac{1}{81}, \frac{1}{243}, \frac{1}{729}, \frac{1}{2187}\) (గుణశ్రేణిని పోడిగించగా)
∴ 7వ పదం 3787 అవుతుంది.

ప్రశ్న23.
4, a, 9 గుణశ్రేణిలో ఉంటే a విలువ ఎంత ?
జవాబు :
4, a, 9 లు G. P. లో ఉంటే \(\frac{a_{2}}{a_{1}}=\frac{a_{3}}{a_{2}}\)
⇒ \(\frac{a}{4}=\frac{9}{a}\) ⇒ a² = 9 × 4 = 36
∴ a = \(\sqrt{36}\) = ± 6.

ప్రశ్న24.
\(\sqrt{3}, \sqrt{12}, \sqrt{27}\) అంకశ్రేఢిలోని తరువాత పదంను రాయండి.
జవాబు :
\(\sqrt{3}, \sqrt{12}, \sqrt{27}=\sqrt{3}, \sqrt{4 \times 3}, \sqrt{9 \times 3}\)
= \(\sqrt{3}, 2 \sqrt{3}, 3 \sqrt{3}\)
∴ తరువాత పదం 4√3 = \(\sqrt{48}\)

ప్రశ్న25.
అంకశ్రేణి యొక్క పదాంతరము ‘2’ అయిన a₁₀ – a₅ విలువ ఎంత?
జవాబు :
d = 2, ∴ a₁₀ – a₅ = 5d = 5(2) = 10

ప్రశ్న26.
గుణశేరిలోని 5వ పదము 32 మరియు 7వ పదము 128. అయిన గుణశ్రేఢి సామాన్య నిష్పత్తిని కనుగొనుము.
జవాబు :
G.P లో a₅ = ar⁴ = 32; a₇ = ar⁶ = 128

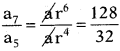
r² = 4 ⇒ r = 4 = ± 2

ప్రశ్న27.
log₂ 2, log₂ 4, log₂ 8 అంకశ్రేణి యొక్క సామాన్య భేదము 1 అని చూపండి.
జవాబు :
log₂ 2 = 1,
log₂ 4 = log₂ 2² = 2 log₂ 2 = 2
∴ a₁ = 1, a₂ = 2
∴ సామాన్య భేదం a₂ – a₁ = 2 – 1 = 1

ప్రశ్న28.
క్రింది సంఖ్యల జాబితాలో అంకశ్రేణి ఏది ?
A) 1, 3, 6, 10, 15, ………
B) 100, 80, 60, 40, …….
C) 2, 4, 8, 16, ……
D) 3, 3, 4, 4, 5, 5, …….
జవాబు :
B) 100, 80, 60, 40, …….

ప్రశ్న29.
క్రింది సంఖ్యల జాబితాలో అంకశ్రేణి కానిది ఏది ?
A) 1, 2, 3, 4, ……..
B) 3, 3, 3, 3, ……..
C) 6, 3, 0, – 3, ……
D) 6, 4, 1, – 3, ……..
జవాబు :
D) 6, 4, 1, – 3, ……..

ప్రశ్న30.
అంకశ్రేణికి ఉదాహరణను రాయండి.
జవాబు :
3, 6, 9, 12, ………….

ప్రశ్న31.
అంకశ్రేణికి చెందిన క్రింది ఏది అసత్యం ?
A) జాబితాలోని రెండు వరుస సంఖ్యల మధ్య గల భేదం స్థిరము.
B) పరిమిత అంకశ్రేణికి చివరి పదము ఉంటుంది.
C) జాబితాలోని రెండు వరుస సంఖ్యల నిష్పత్తి స్థిరము.
D) అపరిమిత అంకశ్రేణికి చివరి పదం ఉండదు.
జవాబు :
C) జాబితాలోని రెండు వరుస సంఖ్యల నిష్పత్తి స్థిరము.

ప్రశ్న32.
5, 2, -1, – 4, ……. శ్రేణిలో k + 1 వ పదము 5 – 3k అయిన kవ పదంను కనుగొనుము.
జవాబు :
5, 2, -1, – 4, ……. అంకశ్రేఢి (A.P.)లో కలవు. .
a = 5, d = 2-5 = -3
a_k+1 = 5 – 3k అయిన
a_k = a_k+1 + (- 3) = 5 – 3k – 3
kవ పదము a_k = 2 – 3k.

ప్రశ్న33.
ఒక అంకశ్రేణిలో a₂₅ – a₂₀ = 60 అయిన a₁₅ – a₁₀ విలువ ఎంత ?
జవాబు :
a₂₅ – a₂₀ = 60 ⇒ 5d = 60 …… (1)
ఇప్పుడు a₁₅ – a₁₀ = 5d = 60 [(1) నుండి]
(లేదా)
a₂₅ – a₂₀ = a₁₅ – a₁₀ = 60

ప్రశ్న34.
4, 10, 16, 22, ….. ఇంకశ్రేణిలో 10వ పదము ఎంత?
జవాబు :
ఇచ్చిన A.P. : 4, 10, 16, 22, ……
a = 4, d = 10 – 4 = 6,
a₁₀ = a + 9d = 4 + 54 = 58
(లేదా)
ఇచ్చిన A.P. ని పొడిగించగా
4, 10, 16, 22, 28, 34, 40, 46, 52, 58
∴ 10వ పదము = 58

ప్రశ్న35.
క్రింది వానిని జతపరచడంలో సరైన సమాధానాన్ని ఎన్నుకొనుము..

i) అంకశ్రేణిలో 1వ పదము	a) arn-1
ii) అంకశ్రేణిలో n పదాల మొత్తం	b) \(\frac{n}{2}\)[2a+(n – 1)d]
iii)గుణ శ్రేణిలో 1వ పదము	c) a + (n – 1)d

A) i-a, ii-b, iii-c
B) i-c, ii-b, iii-a
C) i-c, ii-a, iii- b
D ) i-b, ii-a, iii-c
జవాబు :
B) i-c, ii-b, iii-a

ప్రశ్న36.
\(\frac{1}{4}, \frac{-1}{4}, \frac{-3}{4}, \frac{-5}{4}\) ……. అంకశ్రేణి యొక్క సామాన్య భేదంను కనుగొనుము.
జవాబు :

ప్రశ్న37.
ఒక అంకశ్రేణి మొదటి పదం a = 4, పదాంతరం d =-3 అయిన ఆ శ్రేఢి 4వ పదమును రాయండి.
జవాబు :
a = 4, d = -3.
4వ పదం a_a = a + 3d ,
= 4 + 3(- 3) = 4 – 9 = -5

ప్రశ్న38.
ఇచ్చిన పటంలో x విలువ ఎంత ?

జవాబు :
\(\frac{1}{2}\)

ప్రశ్న39.
2, \(\frac{5}{2}\), 3, \(\frac{7}{2}\), 4, ………… A.P. లో తరువాత పదంను కనుగొనుము.
జవాబు :
2, 1, 3, . , ……. తరువాత పదం
∴ a = 2, d = \(\frac{5}{2}\) – 2 = \(\frac{1}{2}\)
∴ a₆ = a + 5d
= 2 + 5(½) = 2 + \(\frac{5}{2}\) = \(\frac{9}{2}\)
(లేదా)
ఆ శ్రేఢ 2, 2½, 3, 3½, 4, 4½
కావలసిన పదం = 4½ = \(\frac{9}{2}\)

ప్రశ్న40.
3, 3 + √2, 3 + 2√2, 3 + 3√2, ……….. A.P. యొక్క సామాన్య భేదంను కనుగొనుము.
జవాబు :
సామాన్య భేదం d = a₂ – a₂
= (3 + √2) – 3 = √2

ప్రశ్న41.
5, 1, -3, -1, ….. ఒక అంకశ్రేణిని ఏర్పరుస్తాయి అని చూపుము.
జవాబు :
ఇచ్చిన A.P. : 5, 1, – 3, – 7, – 11, – 15,
– 19, – 23, – 27, – 31
(లేదా)
a = 5, d = a₂ – a₁ = 1 – 5 = -4,
a₁₀ = a + 9d = ?
a₁₀ = 5 + 9(-4) = 5 – 36 = -31.

ప్రశ్న42.
√2, √8, \(\sqrt{18}, \sqrt{32}\), ….. అంకశ్రేణి లో తరువాత పదంను రాయండి.
జవాబు :

ప్రశ్న43.
21, 18, 15, …… శ్రేణిలో – 81 ఎన్నవ పదము ?
జవాబు :
a = 21, d = 18 – 21 = -3, a_n = -81,
n = ?
a_n = a + (n – 1)d = – 81
⇒ 21 + (n – 1) (- 3) = – 81
⇒ (n – 1) (- 3) = – 81 – 21 = – 102
⇒ n – 1 = \(\frac{-102}{-3}\) = 34
∴ n = 34 + 1 = 35

ప్రశ్న44.
21, 18, 15, …… A.P. లో సున్న ఎన్నవ పదం అవుతుంది ?
జవాబు :
21, 18, 15, 12, 9, 6, 3, 0, …… (ఇచ్చిన A.P. ని పొడిగించగా).
∴ 8వ పదం సున్న అవుతుంది.
(లేదా)
a_n = a + (n – 1)d = 0
⇒ 21 + (n – 1) (- 3) = 0
⇒ (n – 1) (- 3) = – 21
⇒ n – 1 = \(\frac{-21}{-3}\) = -21
∴ n = 7 + 1 = 8

ప్రశ్న45.
log_a a, log_a a⁴, log_a a⁷, log_a a¹⁰ ………. ఒక
A) గుణశ్రేఢి
B) అంకశ్రేఢి
C) హరాత్మక శ్రేఢి
D) ఏదీకాదు
జవాబు :
B) అంకశ్రేఢి

log_a a, 4 log_a a, 7 log_a a, 10 log_a a గా ఇచ్చిన A.P. ని రాయవచ్చును.
a₂ – a₁ – 4 loga – log a = 3 log a
a₃ – a₂ = 7 log a – 4 log a = 3 log a
a₄ – a₃ = 10 log a – 7 log a = 3 log a
∴ సామాన్య భేదం సమానం. కావున అంకశ్రేణి.
(లేదా)
దత్తాంశము log_a a, log_a a⁴, log_a a⁷, log_a a¹⁰… a₂ – a₁ = log_aa⁴ – log a
= log \(\frac{a^{4}}{a}\) = log a₃

a₃ – a₂ = log_a a⁷ – log_a a⁴
= log \(\frac{a^{7}}{a^{4}}\) = log a³

a₄ – a₃ = log_aa¹⁰ – log_aa⁷
= log \(\frac{a^{10}}{a^{7}}\) = log a³
∴ సామాన్య భేదం సమానం. కావున అంకశ్రే.

ప్రశ్న46.
మొదటి 10 సహజ సంఖ్యల మొత్తం ఎంత ?
జవాబు :
\(\frac{10 \times 11}{2}\) = 55

ప్రశ్న47.
1, 8, 4, 16, 2 సంఖ్యలను r = \(\frac{1}{2}\) అయ్యే విధంగా గుణ శ్రేణిలో అమర్చుము.
జవాబు :
1, 8, 4, 16, 2 లను r = \(\frac{1}{2}\) అయ్యే విధంగా గుణ శ్రేణిలో అమర్చగా
16, 8, 4, 2, 1 (∵ r< 1 కాబట్టి GP అవరోహణ’ క్రమంలో ఉంటుంది.)

ప్రశ్న48.
మొదటి పదం 3.5, పదాంతరము సున్న (0) గా గల అంకశ్రేఢి 108వ పదము ఎంత ?
జవాబు :
a = 3.5, d = 0
∴ a₁₀₈ = a + 107d = 3.5 + 0 = 3.5

ప్రశ్న49.
ఒక A.P. లో a₁ = 2 మరియు a₃ = 18 అయిన a₂ విలువ ఎంత ?
జవాబు :
a₁ = 2, a + 2d = 18 = 2 + 2d = 18
⇒ 2d = 16 ⇒ d = 8
a₂ = a + d = 2 + 8 = 10
(లేదా)
a₂ = \(\frac{a_{1}+a_{3}}{2}=\frac{2+18}{2}\) = 10

ప్రశ్న50.
3, 8, 13, 18, …., 78 శ్రేణిలోని పదాల సంఖ్యను కనుగొనుము.
జవాబు :
3, 8, 13, 18, …., 78
a = 3, 4 = 5, a = 78, n = ?
a_n = a + (n – 1)d = 78
⇒ 3 + (n – 1) 5 = 78
⇒ (n – 1) 5 = 75 ⇒ n – 1 = 15
∴ n = 16.

ప్రశ్న51.
(x + 2), 2x, (2x + 2) లు అంకశ్రేణిలో 3 వరుస పదాలైతే x విలువను కనుగొనుము.
జవాబు :
x + 2, 25, 2x + 2 లు A.P. లో కలవు.
(2x) – (x + 2) = (2x + 2) – 2x
x – 2 = 2 ⇒ x = 4

ప్రశ్న52.
క్రింధి వానిలో ఏవి అంకశ్రేణిలో గల లంబకోణ త్రిభుజ భుజాలు అవుతాయి ?
A) 6, 8, 10
B) 3, 5, 7
C) 2, 4, 6
D) పైవన్నీ
జవాబు :
A) 6, 8, 10

ప్రశ్న53.
7, 13, 19, ……. అంకశ్రేణిలో 10వ పదమును కనుగొనుము.
జవాబు :
a = 7, d = 13 – 7 = 6, a₁₀ = ?
10వ పదం = a + 9d
= 7 + 9(6) = 7 + 54 = 61
(లేదా)
ఇచ్చిన A.P. ని 10 పదాల వరకు పొడిగించగా, 7, 13, 19, 25, 31, 37, 43, 49, 55, 61
10వ పదం a₁₀ = 61

ప్రశ్న54.
– 11, -7, – 3, 1, ….. జాబితా ఒక అంకశ్రేఢి అని నిరూపించండి.
జవాబు :
– 11, -1, -3, 1, 5, …..
a₂ – a₁ = (-7) – (-11) = 4
a₃ – a₂ = (-3) – (-7) = 4
a₄ – a₃ = 1 – (- 3) = 4
సామాన్య భేదం అన్ని సందర్భాలలో సమానం.
∴ అంకశ్రేఢి అవుతుంది.

ప్రశ్న55.
25, 20, 15, ….. శ్రేణిలో ఎన్నవ పదం మొదటి ఋణ సంఖ్య అవుతుంది ?
జవాబు :
25, 20, 15, …… లో మొదటి ఋణ పదం = ?
a = 25, d = 20 – 25 =-5, a_n < 0
a + (n – 1)d < 0
⇒ 25 + (n-1) (-5) < 0
⇒ (n – 1) (-5) < – 25 ⇒ n – 1 > \(\frac{-25}{-5}\) = 5
⇒ n – 1 > 5 = n > 6.
కావున 7వ పదం మొదటి ఋణసంఖ్య అవుతుంది.
(లేదా)
ఇచ్చిన A.P. : 25, 20, 15, 10, 5, 0, – 5
మొదటి ఋణ సంఖ్య 7వ పదము.

ప్రశ్న56.
ఒక అంకశ్రేణి యొక్క n వ పదం a_n = 2n + 3 అయిన 12వ పదంను కనుగొనుము.
జవాబు :
a_n = 2n + 3 ⇒ a₁₂ = 2(12) + 3 = 27

ప్రశ్న57.
ఒక అంకశ్రేణి యొక్క nవ పదము 7 – 2n అయిన ఆ అంకశ్రేఢి సామాన్య భేదంను తెల్పండి.
జవాబు :
a = 7 – 2n
∴ a₁ = 7 – 2(1) = 5
a₂ = 7 – 2(2) = 3
d = a₂ – a₁ = 3 – 5 = – 2.
(లేదా)
a_n = 7 – 2n of n గుణకం = d = – 2

ప్రశ్న58.
x, y, z లు అంకశ్రేణిలో ఉంటే క్రింది ఏది సత్యం ?
A) y = \(\frac{x+z}{2}\)
B) 2y = x + z
C) y – x = z – y
D) పైవన్నీ
జవాబు :
D) పైవన్నీ

ప్రశ్న59.
24, 21, 18, …. అంకశ్రేణి యొక్క S₄ = S₁₃ =78 అయిన ఆ శ్రేఢి యొక్క 5వ పదం నుండి 13వ పదం వరకు గల పదాల మొత్తం ఎంత ?
జవాబు :
0,

S₁₃ = S₄ + S_{(5 నుండి 13 వరకు)},
⇒ S₁₃ – S₄ = S_{(5 నుండి 13 వరకు)} (∵S₁₃ = S₄)
0 = S_{(5 నుండి 13 వరకు)}

ప్రశ్న60.
క్రింది వానిలో అంకశ్రేఢి యొక్క ఏది సత్యం ?
A) a_n = S + S_n-1
B) a_n = a + (n – 1) d
C) S_n = n(2a + (n – 1) d]
D) పైవన్నీ
జవాబు :
B) a_n = a + (n – 1) d

ప్రశ్న61.
ఒక అంకశ్రేణి 17వ పదం, 10వ పదంకన్నా 21 ఎక్కువ అయిన సామాన్యభేదం ఎంత ?
జవాబు :
a₁₇ = a₁₇ + 21 ⇒ a₁₇ – a₁₀ = 21
⇒ 7d = 21 =d = 3

ప్రశ్న62.
1 మరియు 250ల మధ్య గల 4 యొక్క గుణిజాల సంఖ్య ఎంత ?
జవాబు :
1, 250 మధ్యగల 4 యొక్క గుణిజాలు
4, 8, 12, …….., 248
a = 4, d = 8 – 4 = 4, a = 248, n = ?
a_n = a + (n – 1)d = 248
⇒ 4 + (n – 1) 4 = 248
⇒ (n – 1) 4 = 244
n – 1 = \(\frac{244}{4}\) = 61
n = 61 + 1 = 62
1, 250 మధ్యగల 4 యొక్క గుణిజాల సంఖ్య = 62
(లేదా )
1, 250 మధ్యగల గుణిజాలు … (4, 8, 12, 16, 20, ………, 248)
= (4 × 1, 4 × 2, 4 × 3, ….., 4 × 62)
∴ 1, 250 మధ్యగల 4 యొక్క గుణిజాల సంఖ్య = 62

ప్రశ్న63.
ఒక అంకశ్రేఢ a₂ = 6 మరియు a₇ = – 4 అయిన a_n = 0 అయ్యేట్లు n విలువను కనుగొనుము.
జవాబు :
a₇ – a₂ = 5d = (- 4) – (6) = – 10
d = = =-2
a = a₁ = 6 – (-2) = 8, d = -2
a_n = 0, n = ?
a_n = a + (n – 1)d = 0
= 8 + (n – 1) (-2) = 0
= (n – 1) (-2) = -8
= n – 1 = \(\frac{-8}{-2}\) = 4
n = 4 + 1 = 5.
(లేదా)
d = -2
ఆ శ్రేఢి a₁, a₂, a₃, a₄, a₅, a₆, a₇
8, 6, 4, 2, 0, -2, -4
∴ n – 5

ప్రశ్న64.
– 11, – 8, – 5, ……. 49 అంకశ్రేణిలో చివరి 2. నుండి 4వ పదమును రాయండి.
జవాబు :
– 11, – 8, – 5, ……, 49 అంకశ్రేణిలో చివరి నుండి 4వ పదము = 40.
ఆ శ్రేఢి = -11, -8, -5,…… 40, 43, 46, 49

ప్రశ్న65.
a = -1.25, d = -0.25 అయిన a్మను లెక్కించండి.
జవాబు :
a. = – 1.25, d = 0.25
a = a + 3d
= (- 1.25) + 3(-0.25)
= 1.25 – 0.75 = -2,

ప్రశ్న66.
ప్రవచనం-1 : అంకశ్రేఢి యొక్క nవ పదం a_n = a.r^n-1
ప్రవచనం-II : గుణశ్రేఢి యొక్క nవ పదం a_n = a + (n – 1) d
A) I సత్యం, II అసత్యం
B) I అసత్యం, II సత్యం
C) I మరియు II లు రెండూ సత్యం
D) I మరియు II లు రెండూ అసత్యం
జవాబు :
D) I మరియు II లు రెండూ అసత్యం

ప్రశ్న67.
2, 7, 12, ……. అంకశ్రేణిలో 10 పదాల మొత్తం ఎంత ?
జవాబు :
a = 2, d = 7 – 2 = 5, a_n = 10, S_n = ?
S = \(\frac{n}{2}\) [2a + (n – 1)d
= \(\frac{10}{2}\) [4 + 9(5)] = 5(49) = 245

ప్రశ్న68.
ఒక అంకశ్రేణిలో a = 7, a₁₃ = 35 అయిన S₁₃ = 273 అని చూపుము.
జవాబు :
a = 7, a₁₃ = 1 = 35; S₁₃ = ?, n = 13.
S_n = \(\frac{n}{2}\)[a + l]
= \(\frac{13}{2}\) [7+ 35] = 13 × 21 = 273

ప్రశ్న69.
– 37, – 33, – 29, ….. అంకశ్రేణిలో 12 పదాల మొత్తంను కనుగొనుము.
జవాబు :
a = – 37, d = – 33 – (-37) = 4, n = 12 1.
S_n = \(\frac{n}{2}\) [2a + (n – 1)d] .
= \(\frac{12}{2}\) [2(-37) + 11(4)]
= 6 (-74 + 44) = 6 (30) = – 180

ప్రశ్న70.
S = {x/x అనేది 2n + 3, n వ పదంగా గల అంకశ్రేణిలోని పదము, మరియు n < 6} అయిన S సమితిని రోస్టర్ రూపంలో రాయండి.
జవాబు :
a_n = 2n + 3
n = 1, a₁ = 2(1) + 3 = 5,
a₂ = 2(2) + 3 = 7,
a₃ = 2(3) + 3 = 9,……..
S = {5, 7, 9, 11, 13, 15}

ప్రశ్న71.
ఒక త్రిభుజంలోని కోణాలు సామాన్య భేదం 10గా గల అంకశ్రేణిలో ఉంటే ఆ కోణాలను కనుగొనుము.
జవాబు :
మూడు కోణాలు a, a + d, a + 2d అనుకొనుము.
(∵అంకశ్రేఢిలో కలవు), d = 10 మూడు కోణాల మొత్తం .
a + a + d + a + 2d = 180°
3a + 3d = 1800
3a + 30 = 180° ( d = 10)
3a = 180 – 30 = 150°
a = 50°
∴ మూడు కోణాలు 50, 60, 70°.

ప్రశ్న72.
6 చే భాగింపబడే మొదటి 40 ధనపూర్ణ సంఖ్యల మొత్తంను లెక్కించండి.
జవాబు :
6 చే భాగింపబడే మొదటి 40 ధనపూర్ణ సంఖ్యలు
6, 12, 18, ……….., 40 పదాలు
a = 6, d = 12 – 6 = 6, a_n = 40, S_n = ?
S_n = \(\frac{n}{2}\) [2a + (n – 1)d]
= \(\frac{40}{2}\)[12 + 39 × 6]
= 20 × 246 = 4920
(లేదా)
(6 + 12 + 18 + ……. + 40 పదాలు )
= 6(1 + 2 + 3 + 4 + …. + 40]

= 3 × 40 × 41 = 4,920.

ప్రశ్న73.
అంకశ్రేణి n వ పదం an = 9 – 5n అయిన ఆ అంకశ్రేఢి మొదటి 15 పదాల మొత్తం ఎంత ?
జవాబు :
a_n = 9 – 5n
a₁ = a = 9-5(1) = 4
a₂ = 9-5(2) = -1
d = a₂ – a₁ = -1 – 4 = -5
n = 15, S_n = ?
S_n = \(\frac{n}{2}\) [2a + (n – 1)d]
= \(\frac{15}{2}\) [8 + 14 (-5)] = \(\frac{15}{2}\)(-62)
=- 465

ప్రశ్న74.
ఒక అంకశ్రేణిలో n పదాల మొత్తం 2n² + 3n అయిన ఆ అంకశ్రేణి సామాన్యభేదం 4 అని చూపండి.
జవాబు :
S_n = 2n² + 3n
S₁ = a₁ = 2(1)² + 3(1) = 5
S₂ = a₁ + a₂ = 2(2)² + 3(2)
= 8 + 6 = 14
a₂ = 14 – 5 = 9
∴ d = a₂ – a₁ = 9 – 5 = 4

ప్రశ్న75.
ఒక అంకశ్రేణి n పదాల మొత్తం 3n² + 5n అయిన ఆ శ్రేఢి యొక్క 2 వ పదంను రాయండి.
జవాబు :
S_n = 3n² + 5n
S₁ = a₁ = 3(1)² + 5(1) = 8
S₂ = a₁ + a₂ = 3(2)² + 5(2) = 22
a₂ = 22 – a₁ = 22 – 8 = 14
(లేదా)
a₂ = S₂ -S₁
= [3(2)² + 5(2)] – [3(1)² + 5(1)]
= 22 – 8 = 14

ప్రశ్న76.
a₇ = 4, d = 2 మరియు S₈ = – 8 అయిన ఆ శ్రేణిలో S₉ = 0 అని చూపుము.
జవాబు :
a₇ = 4, d = 2
a + 6d = 4 ⇒ a + 6(2) = 4
⇒ a + 12 = 4 .
⇒ a = -8
a = -8, d = 2 .

S_n = \(\frac{n}{2}\)[2a + (n – 1]d]
= \(\frac{9}{2}\)[2 (-8) + (9 – 1) (2)]
= \(\frac{9}{2}\)[- 16 + 16] = 0
∴ S₉ = 0

ప్రశ్న77.
100 నుండి 200 వరకు గల బేసి సంఖ్యల మొత్తం ఎంత ?
జవాబు :
100, 200 మధ్యగల బేసి సంఖ్యలు
101, 103, 105, ….., 199
a = 101, d = 2, a_n = 199, n = ?, S_n = ?
a_n = a + (n – 1)d = 199
⇒ 101 + (n – 1) (2) = 199
⇒ (n – 1) (2) = 199 – 101 = 98
⇒ n – 1 = \(\frac{98}{2}\) = 49
∴ n = 49 + 1 = 50
S = \(\frac{n}{2}\) [2a + (n – 1)d]
= \(\frac{50}{2}\) [202 + 49 × 2]
= 25 × 300 = 7500
(లేదా)
100 నుండి 200 వరకు గల బేసి సంఖ్యల మొత్తం ‘= (1 నుండి 200 వరకు గల బేసి సంఖ్యల మొత్తం)
– (1 నుండి 100 వరకు గల బేసి సంఖ్యల మొత్తం)
= (100)² – (50)² = 10000 – 2500 = 7500

ప్రశ్న78.
మొదటి n బేసి సంఖ్యల మొత్తాన్ని కనుగొనుము.
జవాబు :
1, 3, 5, …, n పదాలు , a = 1, d = 2

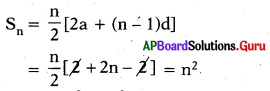
ప్రశ్న79.
క్రింది వానిలో గుణశ్రేఢి ఏది ?
A) 6, 12, 24, ….
B) 1, 4, 9, 16, ……
C) 0, 3, 9, 27, …
D) పైవన్నీ
జవాబు :
A) 6, 12, 24, ….

ప్రశ్న80.
ఒక గుణ శ్రేఢి మొదటి పదం ar² మరియు సామాన్య. నిష్పత్తి r అయిన ఆ శ్రేఢి 5వ పదంను రాయండి.
జవాబు :
మొదటి పదం a = a₁ = ar,
సామాన్య భేదం = r
a₂ = ar³r.r = ar³
a₃ = ar⁴,
a₄ = ar⁵
∴ a₅ = ar⁶
(లేదా)
a_n = ar², r = r, n = 5
∴ a_n = ar^n-1
= as = ar²(r)^5-1 = ar²r⁴
a₅ = ar⁶

ప్రశ్న81.
\(\frac{1}{16}, \frac{1}{64}, \frac{1}{256}\) ….. గుణశ్రేణి సామాన్య నిష్పత్తి ఎంత ?
జవాబు :

ప్రశ్న82.
క్రింది వానిలో సామాన్య నిష్పత్తి 3 గా గల గుణ శ్రేణి ఏది ?
A) 1, 3, 9, 27, ….
B) 5, 15, 45, 135,
C) 2, 6, 18, 54, ..
D) పైవన్నీ
జవాబు :
D) పైవన్నీ

ప్రశ్న83.
x, \(\frac{4 x}{3}, \frac{5 x}{3}, 2 x, \frac{7 x}{3}\) …….. అంకశ్రేణిలో 7వ పదమును కనుగొనుము.
జవాబు :

ప్రశ్న84.
మొదటి పదం a = 3, సామాన్యనిష్పత్తి r = 2 గా గల గుణశ్రేణిని రాయండి.
జవాబు :
a = 3, r = 2గా గల గుణశేథి 3, 6, 12, 24, …

ప్రశ్న85.
64, -32, 16, – 8, … గుణశ్రేఢి అని చూపుము.
జవాబు :
64, -32, 16, – 8, …….
\(\frac{a_{2}}{a_{1}}=\frac{-32}{64}=-\frac{1}{2}, \frac{a_{3}}{a_{2}}=\frac{16}{-32}=-\frac{1}{2}\)
\(\frac{a_{4}}{a_{3}}=\frac{-8}{16}=-\frac{1}{2}\)
∴ సామాన్య భేదం స్థిరము.
∴ ఇచ్చిన సంఖ్యలు గుణశ్రేణిలో కలవు.

ప్రశ్న86.
6 చే భాగింపబడే మొదటి 40 ధనపూర్ణ సంఖ్యల మొత్తము కనుగొనుము. ఈ సమస్యా సాధనా సోపాన క్రమంలో సరైన దానిని ఎన్నుకొనుము.
సోపానం (a) : S_n = A [2a + (n – 1)d] ,
సోపానం (b) : 6చే భాగింపబడే మొదటి 40 ధనపూర్ణ సంఖ్యలు 6, 12, 18, 24, ….., 40 పదాలు
సోపానం (c) : S₄₀ = \(\frac{40}{2}\) [2(6)+ (40 -1)(6)] = 20 [12 + 234]
సోపానం (d) : a = 6, d = a₂ – a₁ = 6, n = 40
సోపానం (e) : S₄₀ = 20 × 246 = 4920
A) b, e, c, a, d
B ) c, b, a, d, e
C) b, a, c, e, d
D) b, d, a, c, e
జవాబు :
D) b, d, a, c, e

ప్రశ్న87.
a = √5, r = \(\frac{1}{5}\) గా గల గుణశ్రేణి యొక్క 2వ పదంను రాయండి.
జవాబు :
a₂, = ar = √5 × \(\frac{1}{5}=\frac{1}{\sqrt{5}}\)

ప్రశ్న88.
-2, 6, – 18, 54, ….. గుణ శ్రేణిలో తరువాతి పదం తెల్పండి.
జవాబు :
– 2, 6, – 18, 54 లో తరువాత పదం a₅ = ?
a = – 2, r =-3
a₅ = a.r⁴ = (-2) (- 3)⁴
=- 2 (81) = – 162

ప్రశ్న89.
x, 1, \(\frac{1}{x}\), … గుణశ్రేణిలో తరువాతి పదంను రాయండి.
జవాబు :
x, 1, \(\frac{1}{x}\)లు గుణశ్రేణిలో కలవు.
a = x, r = \(\frac{a_{2}}{a_{1}}=\frac{1}{x}\)
∴ తరువాత పదం = \(\frac{1}{x} \times \frac{1}{x}=\frac{1}{x^{2}}\)

ప్రశ్న90.
x, 4, 4x లు గుణశ్రేణిలో మూడు వరుస పదాలైతే x విలువను కనుగొనుము.
జవాబు :
x, 4, 4x లు గుణశ్రేణిలో 3 వరుస పదాలు
∴ \(\frac{4}{x}=\frac{4 x}{4} \Rightarrow \frac{4}{x}\)
⇒ 4 = x² = x = √4 = +2

ప్రశ్న91.
అగ్గిపుల్లల సహాయంతో మోహన్ క్రింది ఆకారాలను తయారు చేశాడు. ప్రతి ఆకారానికి వాడిన అగ్గిపుల్లల సంఖ్య వరుసగా ఏ శ్రేణి అవుతుంది ?

జవాబు :
అంకశ్రేణి

ప్రశ్న92.
0.4, 0.04, 0.004, …… గుణశ్రేణి సామాన్య నిష్పత్తిని తెల్పండి.
జవాబు :

ప్రశ్న93.
\(\frac{1}{\sqrt{2}}\), -2, \(\frac{8}{\sqrt{2}}\) …. గుణశ్రేణి తరువాత పదంను గుణశ్రేణి తరువాత పదంను కనుగొనుము.
జవాబు :

ప్రశ్న94.
\(\frac{5}{2}, \frac{5}{4}, \frac{5}{8}\) …….. గుణ శ్రేణిలో nవ పదమును కనుగొనుము
జవాబు :

ప్రశ్న95.
2, 8, 32, …….గుణ శ్రేణిలో ఎన్నవ పదం 512 అవుతుంది ?
జవాబు :
2, 8, 32, …….
a = 2, r = \(\frac{8}{2}\) = 4, a_n = 512, n = ?
a_n = ar^n-1 = 512
⇒ 2(4)^n-1 = 512
⇒ 4^n-1 = \(\frac{512}{2}\) = 256 = 4⁴
∴n – 1 = 4 ⇒ n = 5
∴ 5వ పదం 512 అవుతుంది.
(లేదా)
ఇచ్చిన G.P. ని పొడిగించగా
2, 8, 32, 128, 512, ……
∴ 5వ పదం = 512

ప్రశ్న96.
ఒక గుణ శ్రేఢి 3వ పదం 36 మరియు 6వ పదం 972 అయిన ఆ గుణశ్రేఢి 4వ పదమును కనుగొనుము.
జవాబు :
a₃ = ar² = 36, a₆ = ar⁵ = 972

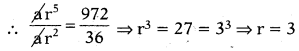
నాల్గవ పదం a₄ = a₃, r = 36 × 3 = 108

ప్రశ్న97.
గుణశ్రేఢి యొక్క n వ పదం కనుగొను సూత్రాన్ని రాయండి.
జవాబు :
గుణ శ్రేఢిలో 1వ పదము a_n = a.r^n-1

ప్రశ్న98.
2, – 6, 18, – 54, ….. గుణ శ్రేఢి n వ పదమును రాయండి.
జవాబు :
2 = 2, r = \(\frac{a_{2}}{a_{1}}=\frac{-6}{2}\) = – 3, a_n = ?
a_n = a.r^n-1 = 2(- 3)^n-1

ప్రశ్న99.
a₁ = 9, r = \(\frac{1}{3}\) గా గల గుణశ్రేణిలో ఇలను కనుగొనుము.
జవాబు :
a₁ = 9, r = \(\frac{1}{3}\)
a₅ = ar⁴ = 9\(\left(\frac{1}{3}\right)^{4}\) = 9 × \(\frac{1}{81}=\frac{1}{9}\)

ప్రశ్న100.
ఒక గుణశ్రేణి యొక్క n వ పదం 3 \(\left(\frac{1}{2}\right)^{n-1}\). ఆ గుణశ్రేణి యొక్క సామాన్య నిష్పత్తి ఎంత ?
జవాబు :
\(\frac{1}{2}\)

ప్రశ్న101.
2, 2√2 , 4, …… గుణశ్రేణిలో ఎన్నవ పదం 64 అవుతుంది ?
జవాబు :
2, 2√2 , 4, ……….
a = 2, r = \(\frac{a_{2}}{a_{1}}=\frac{2 \sqrt{2}}{2}\) = √2 , a_n = 64.
a_n = ar^n-1 = 64
⇒ 2(√2)^n-1 = 64 ⇒ (√2)^n-1 = \(\frac{64}{2}\) = 32
⇒ 2^{\(\frac{\mathrm{n}-1}{2}\)} = 2⁵ ⇒ \(\frac{\mathrm{n}-1}{2}\) = 5
⇒ n – 1 = 10 ⇒ n = 11
(లేదా)
2, 2√2, 4, 4√2, 8, 8√2, 16, 16√2, 32, 32√2, 64 గా రాయవచ్చును.
∴ 11వ పదం 64 అవుతుంది.

ప్రశ్న102.
x – 1, x – 2, x – 3, ….. అంకశ్రేణిలో 10 పదాల మొత్తం ఎంత ?
జవాబు :
x – 1, x – 2, x – 3, ….. (x – 10) అంకశ్రేణిలో 10 పదాల మొత్తం
a = x – 1, d = (x – 2) – (x – 1) = – 1,
n= 10
S_n = \(\frac{n}{2}\) [a + l]
= \(\frac{10}{2}\) [(x-1) + (x – 10)]
S₁₀ =5(2x – 11) = 10x – 55
(లేదా)
(x – 1) + (x – 2) + (x – 3) +…. + (x – 10)
= 10x – (1 + 2 + 3 + …. + 10)
= 10x – \(\frac{10 \times 11}{2}\) = 10x – 55

ప్రశ్న103.
a₁ = – 12, r = \(\frac{1}{3}\) గా గల గుణశ్రేణిలో 6వ పదాన్ని కనుగొనుము.
జవాబు :
a₆ = (- 12) \(\left(\frac{1}{3}\right)^{5}\)
= -12 × \(\frac{1}{3^{5}}=\frac{-4}{3^{4}}=\frac{-4}{81}\)

ప్రశ్న104.
2x, (x + 10), (3x + 2) లు అంకశ్రేణిలో ఉంటే x విలువ ………..
A) 6
B) 3
C) 5
D) 4
జవాబు :
A) 6

2x, (x + 10), (3x + 2) లు A.P లో కలవు.
∴ (x + 10) – (2x) = (3x + 2) – (x + 10)
x + 10 – 2x = 3x + 2 – x – 10.
⇒ 10 – x = 2x – 8
⇒ – x – 2x = – 8 – 10
⇒ – 3x = – 18 ⇒ x = \(\frac{-18}{-3}\) = 6.

ప్రశ్న105.
ప్రాచీన భారతీయ గణితశాస్త్రవేత్త ఆర్యభట్ట యొక్క ప్రసిద్ధ గ్రంథము …………
A) ఆర్యతర్కం
B) ఆర్యభట్టీయం
C) సిద్ధాంత శిరోమణి
D) కరణకుతూహలం
జవాబు :
B) ఆర్యభట్టీయం

ప్రశ్న106.
క్రింది వానిలో ఏది అసత్యం ?
A) అంకశ్రేణిలోని ప్రతి పదానికి ఒక స్థిర సంఖ్యను – కలుపగా వచ్చే ఫలిత జాబితా అంకశ్రేణి.
B) అంకశ్రేణిలోని ప్రతి పదము నుంచి ఒక స్థిరసంఖ్యను తీసివేయగా ఫలిత జాబితా అంకశ్రేణి.
C) అంకశ్రేణిలోని ప్రతి పదాన్ని ఒక స్థిర సంఖ్యతో గుణించగా వచ్చే ఫలిత జాబితా అంకశ్రేణి.
D) అంకశ్రేణిలోని ప్రతి పదాన్ని ఒక స్థిర సంఖ్యతో భాగించగా వచ్చే ఫలిత జాబితా ఒక గుణ శ్రేఢి.
జవాబు :
D) అంకశ్రేణిలోని ప్రతి పదాన్ని ఒక స్థిర సంఖ్యతో భాగించగా వచ్చే ఫలిత జాబితా ఒక గుణ శ్రేఢి.

ప్రశ్న107.
6, 2 – 2, – 6, …… అంకశ్రేణి సామాన్య భేదం ఎంత ?
జవాబు :
సామాన్య భేదం d = a₂ – a₁ = 2 – 6 = -4

ప్రశ్న108.
క్రింది వానిని జతపరుచుము :

i) మొదటి n సహజ సంఖ్యల మొత్తం	a) \(\frac{\mathrm{n}(\mathrm{n}+1)}{2}\)
ii) మొదటి n బేసి సంఖ్యల మొత్తం	b) n2
iii)మొదటి n సరి సంఖ్యల మొత్తం	c) n(n + 1)

A) i-a, ii-b, iii-c
B) i-b, ii-c, iii-a
C) i-c, ii-a, iii-b
D) i-a, ii-c, iii-b
జవాబు :
A) i-a, ii-b, iii-c

ప్రశ్న109.
2x, 3x, 4x, ….. అంకశ్రేణిలో 10వ పదంను రాయండి.
జవాబు :
a = 2x, d = 3x – 2x = x
a₁₀ = a + 9d = 2x + 9x = 11x
(లేదా)
ఇచ్చిన A.P. ని 10 పదాల వరకు రాయగా 2x, 3x, 4x, 5x, 6x, 7x, 8x, 9x, 10x, 11x
10వ పదము a₁₀ = 11x

ప్రశ్న110.
ఒక టాక్సీ మొదటి కి.మీ. ప్రయాణానికి ₹ 20 ల చొప్పున, తరువాత ప్రతి కి.మీ.కు ₹8 ల చొప్పున చెల్లించవలసిన, 15 కి.మీ. ప్రయాణానికి అయ్యే సొమ్మును కనుగొనుము.
జవాబు :
ప్రతి కి.మీ.కి వరుసగా చెల్లించాల్సిన సొమ్ము
= 20, 28, 36, ……… A. P. లో కలదు.
a = 20, d = 8, a₁₅ = ?
a₁₅ = a + 14d.
= 20 + 14(8)
= 20 + 112 = ₹ 132

ప్రశ్న111.
√2, √8, √18 అంకశ్రేణిలో తరువాత పదం ఏది?
జవాబు :
ఇచ్చిన A.P. : √2, √8, √18 , ………
= \(\sqrt{1 \times 2}, \sqrt{4 \times 2}, \sqrt{9 \times 2}\), …….
= √2, 2√2, 3√2, ………..
∴ తరువాత పదం = 4√2 = \(\sqrt{16 \times 2}=\sqrt{32}\)

ప్రశ్న112.
√3, √12, √27 , ….. అంకశ్రేణిలో 5వ పదమును కనుగొనుము.
జవాబు :
√3, √12, √27 , …… A.P లో 5వ పదం.
\(\sqrt{3}, \sqrt{4 \times 3}, \sqrt{9 \times 3}\)….
= 13, 2/3, 3/3, ……..
5వ పదం 5/3 = \(\sqrt{25 \times 3}\) = \(\sqrt{75}\)

ప్రశ్న113.
ఒక గుణశ్రేణి యొక్క 1వ పదం a_n = 3(2)^n-1 అయిన క్రింది వానిని జతపరుచుము.

i) మొదటి పదం a	a) 2
ii) సామాన్య నిష్పత్తి	b) 3
iii)రెండవ పదం a<sub>2</sub>	c) 6
iv)నాల్గవ పదం a<sub>4</sub>	d) 24

A) i-c, ii-b, iii-d, iv-a
B) i-b, ii-a, iii-c, iv-d
C) i-a, ii-c, iii-b, iv-d
D) i-c, ii-a, iii-b, iv-d
జవాబు :
B) i-b, ii-a, iii-c, iv-d

ప్రశ్న114.
log a, log b, log cలు అంకశ్రేణిలో ఉంటే క్రింది వానిలో ఏది నిజం ?
A) log b² = log ac
B) b² = ac
C) 2 log b = log ac
D) పైవన్నీ
జవాబు :
D) పైవన్నీ

ప్రశ్న115.
sin 0°, sin 30°, sin 90° విలువలు వరుసగా ఏ శ్రేడిని ఏర్పరుస్తాయి ?
జవాబు :
0, \(\frac{1}{2}\), 1 [:: sin 0° = 0, sin 30° = \(\frac{1}{2}\), sin 90° = 1]
అంకశ్రేణిని ఏర్పరుస్తాయి.

ప్రశ్న116.
a = 7, d = 3, n = 8 గా గల అంకశ్రేఢి యొక్క a_n+1 ను కనుగొనుము.
జవాబు :
a_n+1 = a₈₊₁
= a₉ = a + 8d = 7 + 8(3) = 31

ప్రశ్న117.
sin 30, sin 90°, cosec 30° విలువలు వరుసగా ఏ శ్రేణిని ఏర్పరుస్తాయి ?
జవాబు :
\(\frac{1}{2}\), 1, sin 30° = \(\frac{1}{2}\), sin 90° = 1, cosec 30° = 2]
గుణశ్రేణిని ఏర్పరుస్తాయి.

ప్రశ్న118.
a₂ = 13, a₄ = 3 గా గల అంకశ్రేణిలో ఇ, విలువ ఎంత ?
జవాబు :
a₃ = \(\frac{a_{4}+a_{2}}{2}=\frac{3+13}{2}\) = 8
a₁, a₂, a₃, a₄, లు A.P.లో కలవు
= a₁, 13, a₃, 3
a₃ – 13 = 3 – a₃
⇒ 2a₃ = 16 ⇒ a₃ = \(\frac{16}{2}\) = 8

ప్రశ్న119.
“చతురస్రం / దీర్ఘచతురస్రంలోని నాలుగు కోణాల విలువలు వరుసగా ఒక గుణ శ్రేణిలో ఉంటాయి” అని రిషి అంటున్నారు. రిషి తెల్పిన ప్రవచనాన్ని సమర్ధించండి.
జవాబు :
చతురస్రం / దీర్ఘచతురస్రంలోని నాలుగు కోణాల ‘విలువలు వరుసగా 90, 90, 90, 90.
\(\frac{a_{2}}{a_{1}}=\frac{90}{90}\) = 1, \(\frac{a_{3}}{a_{2}}=\frac{90}{90}\) = 1, \(\frac{a_{4}}{a_{3}}=\frac{90}{90}\) = 1, \(\) = 1
సామాన్య భేదం అన్ని సందర్భాలలో సమానంగా కలదు. కావున చతురస్ర / దీర్ఘచతురస్ర కోణాలు గుణ శ్రేణిలో ఉంటాయి. కావున రిషి చెప్పిన ప్రవచనంతో ఏకీభవిస్తాను.

ప్రశ్న120.
ఒక అంకశ్రేణి సామాన్య భేదం – 3 మరియు 18వ పదం – 5 అయితే ఆ శ్రేఢి మొదటి పదం ఎంత ?
జవాబు :
d = 3, a₁₈ ⇒ a + 17d = -5
⇒ a + 17(- 3) = . 5
⇒ a = – 5 + 51 = 46

ప్రశ్న121.
క్రింద ఇవ్వబడిన అసత్య ప్రవచనాన్ని సత్య ప్రవచనంగా మార్చి రాయండి.
ప్రవచనం : ఒక అంకశ్రేణిలో n పదాల మొత్తం
S_n = a + (n – 1]d
జవాబు :
ఒక అంకశ్రేణిలో n పదాల మొత్తం =
S_n = \(\frac{n}{2}\) [2a + (n – 1)d]
(లేదా)
S_n = \(\frac{n}{2}\)[a + l]

ప్రశ్న122.
1 నుంచి 100 వరకు గల అన్ని సహజ సంఖ్యల మొత్తాన్ని సూక్ష్మ పద్ధతిలో తెలిపిన గణితశాస్త్రజ్ఞుడు
A) యూలర్
B) ఆర్యభట్ట
C) గాస్
D) రామానుజం
జవాబు :
C) గాస్

ప్రశ్న123.
24, 21, 18, ……. అంకశ్రేణిలో మొదటి నాలుగు పదాల మొత్తం ఎంత ?
జవాబు :
a₁ = 24, a₂ = 21, a₃ = 18,
d = 21 – 24 = -3
a₄ = a + 3d = 24 – 9
a₄ = 15
S₄ = 24 + 21 + 18 + 15 = 78

ప్రశ్న124.
మొదటి n ధనపూర్ణ సంఖ్యల (సహజ సంఖ్యల) మొత్తమునకు సూత్రాన్ని రాయండి.
జవాబు :
\(\frac{n(n+1)}{2}\)

ప్రశ్న125.
a_n = 3 + 2n గా గల అంకశ్రేణిలో 5వ పదంను కనుగొనుము.
జవాబు :
a_n = 3 + 2n, a₅ = 3 + 2(5) = 13

ప్రశ్న126.
వాక్యం X : a, b, c లు అంకశ్రేణిలో ఉంటే b = \(\frac{a+c}{2}\)
వాక్యం Y : a, b, c లు గుణశ్రేణిలో ఉంటే b² = ac
A) X – సత్యం, Y – అసత్యం
B) X – సత్యం, Y – సత్యం
C) X – అసత్యం, Y – సత్యం
D) X – అసత్యం , Y – అసత్యం
జవాబు :
B) X – సత్యం , Y – సత్యం

ప్రశ్న127.
3n + 5 కు 1వ పదంగా గల అంకశ్రేణి సామాన్య భేదం ఎంత ?
జవాబు :
3

ప్రశ్న128.
ఒక అంకశ్రేణి n పదాల మొత్తం
S_n = \(\frac{n}{2}\) [2a + (n – 1)d]., సూత్ర పదాలను వాని వివరణకు జతపరుచుము.

i) a	p) n పదాల మొత్తము
ii) d	q) పదాల సంఖ్య
iii) Sn	r) మొదటి పదం
iv) n	s) సామాన్య భేదం

A) is, ii-p, iii-r, iv-q
B) i-r, ii-p, iii-q, iv-S
C) i-r, ii-s, iii-p, iv-q
D) is, ii-r, iii-p, iv-4
జవాబు :
C) i-r, ii-s, iii-p, iv-q

ప్రశ్న129.
1, 3, 5, 7, 9, ……. శ్రేణిలో మొదటి 20 పదాల మొత్తం …………….
A) 900
B) 100
C) 1600
D) 400
జవాబు :
D) 400

n = 20, S_n = n² = 202 = 400
(∵ 1, 3, 5, ….. బేసి సంఖ్యలు)

ప్రశ్న130.
అంకశ్రేణి n పదాల మొత్తం S_n = n² + 3n అయిన ఆ అంకశ్రేఢి n వ పదము …….
A) 2n
B) 2n – 2
C) 2n + 2
D) 2n – 1,
జవాబు :
S_n = n² + 3n
a_n = S_n – S_n-1
= (n² + 3n) – [[n – 1)² + 3(n – 1)]
= (n² + 3n) – [n² – 2n + 1 + 3n – 3]
= n² + 3n – (n² + n – 2)
= n² + 3n – n² – n + 2
= 2n + 2
(లేదా)
S_n = n² + 3n
a₁ = S₁ = (1)² + 3(1) = 4
S₂ = a₁ + a₂
= (2)² + 3(2) = 4 + 6 = 10

∴ a₂ = 10 – 4 = 6
d = a₂ – a₁ = 6 – 4 = 2
a_n = a + (n – 1)d
= 4 + (n – 1)2 = 2n + 2

ప్రశ్న131.
అంకశ్రేఢ nపదాల మొత్తం S_n = n² + 5n అయిన ఆ అంకశ్రేఢి 7వ పదమును కనుగొనుము.
A) 16
B) 18
C) 20
D) 22
జవాబు :
B) 18

S_n = n² + 5n, a₇ = ?
a₇ = S₇ – S₆
= [[7)² + 5(7)] – [[6)² + 5(6)]
= 84 – 66 = 18

ప్రశ్న132.
ఒక అంకశ్రేణిలో n పదాల మొత్తం S_n = an² + 5n అయిన క్రింది వానిని జతపరుచుము.

i) మొదటి పదము a	a) 450
ii) సామాన్య భేదం d	b) 9
iii)10 పదాల మొత్తం S10	c) 17
iv) రెండవ పదము a2	d) 8.

A) i-c, ii-b, iii-d, iv-a.
B) i-b, ii-d, iii-a, iv-c
C) i-a, ii-b, iii-c, iv-d
D) i-d, ii-b, iii-c, iv-a
జవాబు :
B) i-b, ii-d, iii-a, iv-c

ప్రశ్న133.
వాక్యం X : అంకశ్రేణిలోని ప్రతి పదాన్ని స్థిర సంఖ్య (ఒకే సంఖ్య)తో గుణించగా ఏర్పడు సంఖ్యల జాబితా తిరిగి అంకశ్రేణి అవుతుంది.
వాక్యం Y : అంకశ్రేణిలోని ప్రతి పదాన్ని ఒక స్థిర సంఖ్యతో భాగించగా వచ్చు నూతన సంఖ్యల జాబితా తిరిగి అంకశ్రేఢి అవుతుంది.
A) X, Y లు రెండూ సత్యం
B) X, Y లు రెండూ అసత్యం
C) X – సత్యం, Y – అసత్యం
D) X – అసత్యం , Y – సత్యం
జవాబు :
C) X – సత్యం, Y – అసత్యం

ప్రశ్న134.
125, – 25, 5, ……. గుణశ్రేణి నాల్గవ పదమును రాయండి.
జవాబు :
a = 125, r = \(\frac{a_{2}}{a_{1}}=\frac{-25}{125}=\frac{-1}{5}\)
a₄ = a₃r = 5 × \(\frac{-1}{5}\) = -1

ప్రశ్న135.
ఒక గుణశ్రేణి మొదటి పదం \(\frac{1}{64}\), సామాన్య నిష్పత్తి 2 అయిన ఆ గుణ శ్రేఢి 9వ పదము ఎంత ?
జవాబు :
a = \(\frac{1}{64}\), r = 2,
a₉ = ar⁸ = \(\frac{1}{64}\) × 2⁸ = \(\frac{1}{2^{6}}\) × 2⁸
= 2² = 4

ప్రశ్న136.
సామాన్య నిష్పత్తి 2గా గల ఒక గుణ శ్రేణిని రాయండి.
జవాబు :
r = 2 గా గల ఒక గుణశ్రేఢి 3, 6, 12, 24, …..

ప్రశ్న137.
3, -3², 3³, ……….. గుణ శ్రేణిలో సామాన్య నిష్పత్తి ఎంత ?
జవాబు :
-3

ప్రశ్న138.
\(\frac{1}{3},-\frac{1}{6}, \frac{1}{12}\) గుణశ్రేణిలో తరువాత పదం ఏది ?
జవాబు :
\(\frac{1}{24}\)

ప్రశ్న139.
ఒక గుణశ్రేఢిలో 3వ పదం 24 మరియు 6వ పదం 192 అయిన ఆ గుణశ్రేణి సామాన్య నిష్పత్తి ఎంత ?
జవాబు :
G.P. లో a₃ = ar² = 24, a₆ = ar⁵ = 192
\(\frac{a_{6}}{a_{3}}=\frac{a r^{5}}{a r^{2}}=\frac{192}{24}\) ⇒ r³ = 8 = 2³
∴ r = 2

ప్రశ్న140.
2, 2√2, 4, ….. గుణశ్రేణిలో 6వ పదం ఏది ?
జవాబు :
2, 2√2, 4 ను 6 పదాల వరకు పొడిగించగా
2, 2√2, 4, 4√2, 8, 8√2.

ప్రశ్న141.
గుణశ్రేణి యొక్క క్రింది వానిని జతపరుచుము.
√3, √6, 2√3, 2√6, …………

i) మొదటి పదం a	a) 4√3
ii) సామాన్య నిష్పత్తి r	b) √3
iii)3వ పదము a3	c) 2√3
iv) 5వ పదము a5	d) √2

A) i-a, ii-c, iii-b, iv-d
B) i-b, ii-a, iii-d, iv-c
C) i-b, ii-d, iii-c, iv-a
D) i-b, ii-a, iii-c, iv-d
జవాబు :
C) i-b, ii-d, iii-c, iv-a

ప్రశ్న142.
√3, √6, 2√3, ……. గుణశ్రేణి సామాన్య నిష్పత్తి √2 అని చూపుము.
జవాబు :

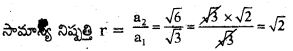
ప్రశ్న143.
1, \(-\frac{1}{3}, \frac{1}{9},-\frac{1}{27}\) ……. గుజశ్రేణిలో 6వ పదమును కనుగొనుము.
జవాబు :

ప్రశ్న144.
p) 1, \(\frac{1}{2}, \frac{1}{4}, \frac{1}{8}\) …………….
q) 1, 2, 4, 8, …….. అయితే
A) p-గుణ శ్రేణి, q-అంకశ్రేణి
B) p, q లు రెండూ అంకశ్రేఢులు
C) p, q లు రెండూ గుణ శ్రేఢులు
D) p-అంకశ్రేణి, q-గుణ శ్రేడి C
జవాబు :
C) p, q లు రెండూ గుణ శ్రేఢులు

ప్రశ్న145.
x, y, z లు గుణశ్రేణిలో ఉంటే,
i) y² = xz
ii) 2 log y = log x + log z
A) i – మాత్రమే సత్యం
B) ii – మాత్రమే సత్యం
C) i మరియు ii సత్యం
D) i మరియు ii లు రెండూ అసత్యం
జవాబు :
C) i మరియు ii సత్యం

ప్రశ్న146.
3, 5, 7, 9, ……… 201 అంకశ్రేణిలో చివరి నుండి 5వ పదంను రాయండి.
జవాబు :
3, 5, 7, 9, ……., 201 అంకశ్రేణిలో చివరి నుండి 5వ పదం
ఇచ్చిన A.P ని చివరి నుండి రాయగా
201, 199, 197, 195, 193, ……., 9, 7, 5, 3
చివరి నుండి 5వ పదం 193.

ప్రశ్న147.
a_n = 3n + 7 అంకశ్రేణిలో మొదటి పదము ఏది?
జవాబు :
a_n = 3n +7
∴ a₁₅ = 3(1) + 7 = 10.

ప్రశ్న148.
a_n = 3 + 4n అంకశ్రేణిలో 15వ పదం ఏది ?
జవాబు :
a_n = 3 + 4n
∴ a₁₅ = 3 + 4(15) = 63.

ప్రశ్న149.
p(x) = (x + 1) (x – 2) (x – 5) ఘన బహుపది యొక్క శూన్యాలు ఏ శ్రేణిలో ఉంటాయి ?
జవాబు :
p(x) శూన్యాలు, -1, 2, 5 లు అంకశ్రేణిలో ఉంటాయి.

ప్రశ్న150.
A అనేది a_n = 2n గా గల అంకశ్రేణిలో మొదటి ‘నాలుగు పదాలుగా గల సమితి, B అనేది a = 2^n-1గా గల గుణశ్రేఢిలో మొదటి నాలుగు పదాలుగా గల సమితి అయిన A ∩ B సమితిని కనుగొనుము.
A) {2, 4, 8}
B) {2, 4, 6, 8}
C) {1, 2, 4, 8}
D) {1, 2, 4, 6, 8}
జవాబు :
A) {2, 4, 8}

A = {2, 4, 6, 8}, B = {1, 2, 4, 8}
A ∩ B = {2, 4, 8}

ప్రశ్న151.
5\(\left(\frac{1}{3}\right)^{n-1}\) n వ పదంగా గల గుణశ్రేణిలో 4వ పదంను కనుగొనుము.
జవాబు :
a_n = 5\(\left(\frac{1}{3}\right)^{n-1}\)

ప్రశ్న152.
\(\frac{1}{16}, \frac{1}{8}, \frac{1}{4}\) ……. గుణశ్రేణిలో మొదటి పూర్ణసంఖ్య ఏది ?
జవాబు :
ఇచ్చిన G.P. = \(\frac{1}{16}, \frac{1}{8}, \frac{1}{4}, \frac{1}{2}\),1, 2, 3, ….. గా రాయవచ్చును.
∴ ఇచ్చిన G.P లో 1 మొదటి పూర్ణసంఖ్య అవుతుంది.

ప్రశ్న153.
A అనేది a_n = 2n గా గల అంకశ్రేణిలో మొదటి నాలుగు పదాలుగా గల సమితి, B అనేది a_n = 2^n-1 గా గల గుణశ్రేణిలో మొదటి నాలుగు పదాలుగా గల సమితి అయిన A ∪ B ని కనుగొనుము.
జవాబు :
A ∪ B = {1, 2, 4, 6, 8}

ప్రశ్న154.
ఒక AP నందలి ప్రతీ పదాన్ని 3 చే గుణించినపుడు ఏర్పడిన అంకశ్రేణి నందు పదాంతరం ……….. రెట్లు పెరుగును.
జవాబు :
3

→ గమనిక : “ఒక ఆటో మొదటి కి.మీ. ప్రయాణానికి ₹30, ఆపై ప్రతి కి.మీ. ప్రయాణానికి ₹ 10 చొప్పున చెల్లించవలసి యున్నది”. పై సమాచారం ఆధారంగా 155-158 వరకు గల ప్రశ్నలకు సమాధానాలు రాయండి.

ప్రశ్న155.
ప్రతి కి.మీ. చెల్లించాల్సిన సొమ్ము జాబితా రాయండి.
జవాబు :
30, 40, 50, 60, 70, 80, ……

ప్రశ్న156.
ఏర్పడిన జాబితా ఏ శ్రేణిలో ఉంటుంది ?
జవాబు :
అంకశ్రేణి

ప్రశ్న157.
ఏర్పడిన జాబితాలో సామాన్య భేదం ఎంత ?
జవాబు :
d = a₂ – a₁ = 40 – 30 = 10

ప్రశ్న158.
ఆటోలో 3 కి.మీ. ప్రయాణించినచో చెల్లించాల్సిన సొమ్ము ఎంత ?
జవాబు :
3 కి.మీ. ప్రయాణానికి చెల్లించాల్సిన సొమ్ము
a₃ = 50

ప్రశ్న159.
ఒక GP నందు 5వ పదం a₅, 6వ పదం a్య అయిన (a₅) (a₆) విలువ క్రింది వానిలో దేనికి సమానం ?
A) a.a₇
B) a(a₁₁)
C) a(a₁₀)
D) a(a₁₂)
జవాబు :
C) a(a₁₀)

a₅ = art, a₆ = ars
= a₅.a₆ = a².r⁹ = a.ar⁹ = a.a₁₀

ప్రశ్న160.
4, x, 9 లు GP లో ఉన్న x విలువ ఎంత ?
జవాబు :
4, x, 9 లు G.P లో ఉంటే \(\frac{x}{4}=\frac{9}{x}\) = x² = 36
∴ x = \(\sqrt{36}\) = ± 6.

ప్రశ్న161.
AP నందు 8వ పదం 10, 18వ పదం 15 అయిన సామాన్య భేదంను కనుగొనుము.
జవాబు :
a₈ = 10, a₁₈ = 15,
a₁₈ – a₈ = 10d = 15 – 10 = 5
∴ d = \(\frac{5}{10}=\frac{1}{2}\)

ప్రశ్న162.
a, b ల మధ్య ‘n’ పదాలుండేటట్లు ఒక అంకశ్రేణి ఉంటే ఆ శ్రేణి సామాన్య భేదం
A) \(\frac{b-a}{n+1}\)
B) \(\frac{a+b}{n-1}\)
C) \(\frac{b-a}{n-1}\)
D) \(\frac{b+a}{n-1}\)
జవాబు :
A) \(\frac{b-a}{n+1}\)

ప్రశ్న163.
క్రిందివానిలో √3 సామాన్య నిష్పత్తిగా గల గుణశ్రేణి
A) 3, 9, 27, …..
B) √3, 3, 3√3, ….
C) 3, \(\frac{1}{3}, \frac{1}{9}\)
D) √3, 2√3, 3√3, ….
జవాబు :
B) √3, 3, 3√3, ….

→ గమనిక : “ఒక గుణశ్రేణి యొక్క 1వ పదం a_n = a.r^n-1 పై సమాచారం ఆధారంగా 164-166 వరకు గల ప్రశ్నలకు సమాధానాలు రాయండి.

ప్రశ్న164.
పై సూత్రంలో ‘r’ దేనిని సూచిస్తుంది ?
జవాబు :
సామాన్య నిష్పత్తి

ప్రశ్న165.
a = 3, r = 3 అయిన 2, విలువ ఎంత ?
జవాబు :
a₃ = 3(√3)^3-1 = 3(√3)² = 9

ప్రశ్న166.
n + 1వ పదం a_n+1 ను కనుగొనుము.
జవాబు :
a_n+1 = a(r)^{(n + 1) – 1} = ar_n

ప్రశ్న167.
5, 10, 20, 40,……….. గుణశ్రేణిలో 120 ఒక పదంగా ఉండదని చూపండి.
జవాబు :
ఇచ్చిన G.P లో a = 5, r = \(\frac{a_{2}}{a_{1}}=\frac{10}{5}\) = 2
a 5 ఇచ్చిన G.P ని పొడిగించగా 5, 10, 20, 40, 80, 160, 320, …..
కావున 120 ఇచ్చిన G.Pలో ఒక పదంగా ఉండదు.

ప్రశ్న168.
అంకశ్రేణిలో గల 6వ, 7వ, 8వ పదాల మొత్తం 678 అయిన 7వ పదం ఎంత ?
జవాబు :
a₆ + a₇ + a₈ = (a + 5d) + (a + 6d) + (a + 7d) = 678
= 3a + 18d = 3(a + 6d) = 678
= 3 . a₇ = 678
= a₇ = \(\frac{678}{3}\) = 226.

ప్రశ్న169.
ఏదైనా శ్రేఢి (GP | AP) నందు S₁₀ – S₉ విలువ ఆ శ్రేఢి ఎన్నవ పదానికి సమానము ?
జవాబు :
10వ పదము.

ప్రశ్న170.
ఒక గుణ శ్రేణిలో a_n7 = (- 1)ⁿ. 2020 అయిన ఆ శ్రేణి సామాన్య నిష్పత్తిని కనుగొనుము.
జవాబు :
a_n = (-1)ⁿ 2020, :
a₁ = – 2020, a₂ = 2020
సామాన్య భేదం r = \(\frac{\mathrm{a}_{2}}{\mathrm{a}_{1}}=\frac{2020}{-2020}\) = -1

ప్రశ్న171.
3⁴ × 3⁸ × 3¹² ….. (16 పదాలు) లబ్దం
A) 3⁵⁴⁴
B) 3⁶⁴
C) 3⁴⁵⁶
D) 3¹⁶
జవాబు :
A) 3⁵⁴⁴

3⁴ × 3⁸ × 3¹² ….. 16 పదాలు
= 3^{4 + 8 + 12 …….. (16 పదాలు)} ……. (1)
ఇపుడు 4 + 8 + 12 + ……. + 16
a = 4, d = 4, n = 16, S_n = ?
S_n = \(\frac{n}{2}\)[2a + (n – 1 d]

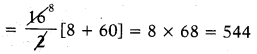
∴ లబ్దం = 3⁵⁴⁴

ప్రశ్న172.
(1 + 5) + (4 + 9) + (7 + 13) + ………….. (10 పదాలు) మొత్తం ఎంత ?
జవాబు :
(1 + 5) + (4 + 9) + (7 + 13) + …. 10 పదాల మొత్తం
= 6 + 13 + 20 + ……. 10 పదాలు A.P లో కలవు.
a = 6, d = 13 – 6 = 7, n = 10

S_n = \(\frac{n}{2}\) [2a + (in = 1)d]
= \(\frac{10}{2}\) [12 + 63] = 5(75) = 375

ప్రశ్న173.
x, y, 2 లు అంకశ్రేణిలో కలవు. y = 46 అయిన x + y + Z విలువ ఎంత ?
జవాబు :
x, y, 2 లు A.P లో ఉంటే
y – x = z – y = 2y = x + Z,
∴ x + y + 7 = 3y = 3 (46) = 138

ప్రశ్న174.
p, q, r లు AP లో కలవు. q = 40 అయిన p+ r విలువ ఎంత ?
జవాబు :
p, q, r లు A.P లో కలవు.
∴ 2q = p + r
∴ p + r = 2(40) = 80

ప్రశ్న175.
x, y, z లు GP లో గలవు. y = 14 అయిన xz విలువను కనుగొనుము.
జవాబు :
x, y, z లు G.P లో ఉంటే
\(\frac{y}{x}=\frac{z}{y}\) ⇒ y²= (14)² = 196

ప్రశ్న176.
p, q, r లు GP లో గలవు. q = 12 అయిన pqr + 1 విలువ కనుగొనుము.
జవాబు :
p, q, r లు G.P లో ఉంటే q² = pr
par = q = (12)³ = 1728
∴ pqr + 1 = 1729.

ప్రశ్న177.
3, 7, 9, 12, ….. ఒక అంకశ్రేణి. (సత్యం / అసత్యం )
జవాబు :
అసత్యం

ప్రశ్న178.
ఒక AP నందు మొదటి ‘n’ పదాల మొత్తం S_n = 4n² + 5n అయిన మొదటి పదం ఎంత ?
జవాబు :
a₁ = S₁ = 4(1)² + 5(1) = 9

ప్రశ్న179.
a మొదటి పదం, 1 చివరి పదంగా గల అంకశ్రేఢి n- పదాల మొత్తం S_n = \(\frac{n}{2}\)(a + l) (సత్యం / అసత్యం)
జవాబు :
సత్యం

ప్రశ్న180.
tan A, tan B, tan C లు G.P. లో ఉండిన cot A, cot B, cot C లు గుణశ్రేఢిలో ఉండును అని చూపుము.
జవాబు :
tan A, tan B, tan C లు G.P. లో కలవు.
⇒ \(\frac{\tan \mathrm{B}}{\tan \mathrm{A}}=\frac{\tan \mathrm{C}}{\tan \mathrm{B}}\)
⇒ tan B’ cot A = tan C . cot B.
⇒ \(\frac{\cot A}{\cot B}=\frac{\cot B}{\cot C}\) (‘: సామాన్య నిష్పత్తి సమానం)
∴ cot A, cot B, cot C లు G.P. లో కలవు.

ప్రశ్న181.
అపరిమిత అంకశ్రేణికి ఒక ఉదాహరణనిమ్ము.
జవాబు :
అపరిమిత అంకశ్రేణికి ఒక ఉదాహరణ : 1, 3, 5, 7, 9, ……….

ప్రశ్న182.
పరిమిత గుణశ్రేణికి ఒక ఉదాహరణనిమ్ము.
జవాబు :
పరిమిత గుణ శ్రేణికి ఒక ఉదాహరణ :
1, 3, 9, 27, ………..

ప్రశ్న183.
రెండు అంకశ్రేఢుల యొక్క ‘n’ వ పదాల నిష్పత్తి 2n + 3 : 4n + 5 అయిన ఆ రెండు శ్రేఢుల ’10’ వ పదాల యొక్క నిష్పత్తి ఎంత ?
జవాబు :
రెండు అంకశ్రేఢుల nవ పదాల నిష్పత్తి
\(\frac{a_{n}}{A_{n}}=\frac{2 n+3}{4 n+5}\)
∴ \(\frac{\mathrm{a}_{10}}{\mathrm{~A}_{10}}=\frac{2(10)+3}{4(10)+5}=\frac{23}{45}\)
10వ పదాల నిష్పత్తి = 23 : 45
(లేదా)
1వ శ్రేణిలో 10వ పదం
= a_n = 2n + 3 = 2(10) + 3 = 23
2వ శ్రేణిలో 10వ పదం
= a_n = 4n + 5 = 4(10) + 5 = 45
10వ పదాల నిష్పత్తి = 23:45

ప్రశ్న184.
cos2 60, cos- 45, cos2 30 లు అంకశ్రేణిలో కలవు అని చూపండి.
జవాబు :
cos² 60 = \(\left(\frac{1}{2}\right)^{2}=\frac{1}{4}\)
cos² 45 = \(\left(\frac{1}{\sqrt{2}}\right)^{2}=\frac{1}{2}\)
cos² 30 = \(\left(\frac{\sqrt{3}}{2}\right)^{2}=\frac{3}{4}\)
∴ cos² 60, cos² 45, cos² 30 విలువల జాబితా \(\)
a₂ – a₁ = \(\frac{1}{2}-\frac{1}{4}=\frac{1}{4}\)
a₃ – a₂ = \(\frac{3}{4}-\frac{1}{2}=\frac{1}{4}\)
సామాన్య భేదం సమానం కావున అంకశ్రేణిలో ఉంటాయి.

ప్రశ్న185.
3⁵, 3⁷, 3⁹ లు గుణశ్రేణిలో కలవు. పై ప్రవచనాన్ని సమర్థించండి.
జవాబు :
\(\frac{a_{2}}{a_{1}}=\frac{3^{7}}{3^{5}}\) = 3²
\(\frac{a_{3}}{a_{2}}=\frac{3^{9}}{3^{7}}\) = 3²
సామాన్య నిష్పత్తి సమానము.
∴ కావున GPలో ఉంటాయి.

ప్రశ్న186.
1, 4, – 2, 10, 7 లు అంకశ్రేణిలో ఉండునట్లు అమర్చుము.
జవాబు :
1, 4, – 2, 10, 7 లను అంకశ్రేణిలో అమర్చగా
-2, 1, 4, 7, 10 (లేదా) 10, 7, 4, 1, -2

→ గమనిక : “2020 సంవత్సరం క్యాలెండర్ నవంబర్ నెలలో మొదటి ఆదివారం 1వ తేదీన వచ్చినది”.
పై సమాచారం ఆధారంగా 187-190 వరకు గల ప్రశ్నలకు సమాధానాలు రాయండి.

ప్రశ్న187.
నవంబర్ 2020 క్యాలెండర్ నందు ఆదివారము వచ్చు తేదీలను సూచించు సంఖ్యల జాబితా రాయండి.
జవాబు :
ఆదివారం వచ్చు తేదీల సంఖ్యల జాబితా
1, 8, 15, 22, 29.

ప్రశ్న188.
పై జాబితా ఏ శ్రేణి అవుతుంది ?
జవాబు :
పై జాబితా అంకశ్రేఢి అవుతుంది.

ప్రశ్న189.
పై జాబితా యొక్క సామాన్య భేదం ఎంత ?
జవాబు :
d = a₂ – a₁ = 8 – 1 = 7,

ప్రశ్న190.
పై జాబితాలో 30 ఒక పదం అవుతుందా ? కాదా ? .
జవాబు :
పై జాబితాలో 30 ఒక పదం కాదు.

ప్రశ్న191.
క్రింది పటంలో ఇవ్వబడిన త్రిభుజ భుజాల మధ్య బిందువులను కలుపుతూ ఏర్పడిన వరుస త్రిభుజాల చుట్టుకొలతలు ఏ రకమైన శ్రేణిని ఏర్పరుస్తాయి ?

జవాబు :
గుణశ్రేణి.