Practice the AP 10th Class Maths Bits with Answers 5th Lesson వర్గ సమీకరణాలు on a regular basis so that you can attempt exams with utmost confidence.
AP Board 10th Class Maths Bits 5th Lesson వర్గ సమీకరణాలు
ప్రశ్న 1.
px + qx2 + r = 0 వర్గ సమీకరణ విచక్షణిని తెల్పండి.
జవాబు.
q2 – 4pr
ప్రశ్న 2.
2x2 – 4x – 3 = 0 యొక్క విచక్షణిని కనుగొనుము.
సాధన.
b2 – 4ac = (- 4)2 – 4(2) (- 3) = 40 .
![]()
ప్రశ్న 3.
చరరాశి X లో వర్గ సమీకరణం యొక్క సాధారణ రూపంను రాయండి.
జవాబు.
ax2 + bx + c = 0, (a ≠ 0) .
ప్రశ్న 4.
సాధారణంగా వర్గ సమీకరణానికి గల మూలాల సంఖ్య ……………………..
(A) గరిష్టంగా మూడు
(B) గరిష్టంగా రెండు
(C) అనంతం
(D) గరిష్ఠంగా ఐదు
జవాబు.
(B) గరిష్టంగా రెండు
ప్రశ్న 5.
క్రింది ఏ సందర్భంలో px2 + qx + r = 0 వర్గసమీకరణం మూలాలు కల్పితాలు అవుతాయి ?
(A) q2 > 4pr
(B) q2 < 4pr
(C) q2 = 4pr
(D) p = q + r
జవాబు.
(B) q2 < 4pr
ప్రశ్న 6.
2x2 + x – 4 = 0 యొక్క విచక్షణిని లెక్కించండి.
సాధన.
విచక్షణి b2 – 4ac = (1)2 – 4(2) (-4)
= 1 + 32 = 33
ప్రశ్న 7.
ax2 + bx + c = 0 యొక్క మూలాల లబ్ధం …..
(A) [latex]\frac{c}{a}[/latex]
(B) [latex]\frac{-b}{a}[/latex]
(C) [latex]\frac{-c}{a}[/latex]
(D) [latex]\frac{b}{c}[/latex]
జవాబు.
(A) [latex]\frac{c}{a}[/latex]
![]()
ప్రశ్న 8.
‘x’ యొక్క ఏ ధనాత్మక విలువకు 4x2 – 9 = 0 అవుతుంది ?
సాధన.
4x2 – 9 = 0 ⇒ 4x2 = 9
⇒ x2 = [latex]\frac{9}{4}[/latex]
⇒ x = [latex]\sqrt{\frac{9}{4}}[/latex] = ± [latex]\frac{3}{2}[/latex]
ప్రశ్న 9.
క్రిందివానిలో మూలాలు సమానంగా గల వర్గ
సమీకరణం ఏది ?
(A) x2 – 5 = 0
(B) x2 – 10x + 25 = 0
(C) x2 + 5x + 6 =:0
(D) x2 – 1 = 0
జవాబు.
(B) x2 – 10x + 25 = 0
ప్రశ్న 10.
క్రింది వానిలో [latex]\frac{1}{3}[/latex] మరియు [latex]\frac{1}{2}[/latex] లను మూలాలుగాకలిగిన వర్గ సమీకరణం ఏది ?
(A) x2 + [latex]\frac{5 x+1}{6}[/latex] = 0
(B) – 6x2 – 5x + 1 = 0
(C) x2 – [latex]\frac{5 x-1}{6}[/latex] = 0
(D) 6x2 – 5x -1 = 0
సాధన.
(C) x2 – [latex]\frac{5 x-1}{6}[/latex] = 0
ప్రశ్న 11.
x2 – px + q = 0 (p, q ∈ R మరియు p ≠ 0, q ≠ 0)కు విభిన్న వాస్తవ మూలాలు ఉంటే క్రింది వానిలో ఏది సత్యం ?
(A) p2 < 4q
(B) p2 > 4q
(C) p2 = 4q
(D ) p2 + 4q = 0
జవాబు.
(B) p2 > 4q
ప్రశ్న 12.
ax2 + bx + c = 0 వర్గ సమీకరణంలో b2 – 4ac> 0 అయిన దాని మూలాల స్వభావాన్ని తెల్పండి.
జవాబు.
అసమాన వాస్తవ సంఖ్యలు.
ప్రశ్న 13.
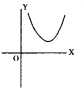
క్రింది ఏ సందర్భంలో ax2 + bx + c = 0 రేఖాచిత్రము ఇచ్చిన పటాన్ని పోలి ఉంటుంది ?
(A) b2 – 4ac > 0
(B) b2 – 4ac = 0
(C) b2 – 4ac < 0
(D) ఏదీకాదు
జవాబు.
(A) b2 – 4ac > 0
![]()
ప్రశ్న 14.
2 + √3, 2 – √3 మూలాలుగా గల వర్గ సమీకరణమును రాయండి.
సాధన.
x2 – (α + β)x + αβ = 0 .
α = 2 + √3, β = 2 – √3
x2 – 4x + 1 = 0
ప్రశ్న 15.
x2 + 6x + 5 = 0 మూలాలు α మరియు β అయిన α + β విలువ ఎంత ?
సాధన.
α + β = [latex]\frac{-b}{a}[/latex] = [latex]\frac{-6}{1}[/latex] = – 6
ప్రశ్న 16.
x2 – 10x + 9 = 0కు α, β లు మూలాలైతే |α – β| విలువ ఎంత ?
సాధన.
x2 – 10x + 9 = 0కు α, β లు మూలాలు.
α + β = [latex]\frac{-b}{a}[/latex] = [latex]\frac{-(-10)}{1}[/latex] = 10
α, β = [latex]\frac{\mathrm{c}}{\mathrm{a}}[/latex] = 9
(α – β)2 = (α + β)2 – 4ap .
= (10)2 – 4(9) = 100 – 36 = 64
α – β = √64 = ± 8
∴ |α – β| = 8
ప్రశ్న 17.
ax2 + ax + 2 = 0 మరియు x2 + x + b = 0 అనే వర్గ సమీకరణాలకు ఒకటి ఒక ఉమ్మడి మూలం అయితే a ∙ b = 2 అని చూపుము.
సాధన.
ax2 + ax + 2 = 0 కు 1 ఒక మూలం.
a(1)2 + a(1) + 2 = 0
∴ 2a + 2 = 0 ⇒ a = – 1
అలాగే x2 + x + b = 0 కి కూడా 1 ఒక మూలము.
∴ 1 + 1 + b = 0 ⇒ b = – 2.
∴ a : b = (-1) (-2) = 2.
ప్రశ్న 18.
6x2 – 5x + 1 = 0 యొక్క విచక్షణి విలువను కనుగొనుము.
సాధన.
విచక్షణి b2 – 4ac = (-5)2 – 4(6)(1) = 1
ప్రశ్న 19.
క్రింది వానిలో ఏది x – [latex]\frac{3}{x}[/latex] = 2 సమీకరణం యొక్క ఒక మూలము ?
(A) 1
(B) 2
(C) 3
(D) 4
జవాబు.
(C) 3
![]()
ప్రశ్న 20.
x2 + 5x + k = 0 సమీకరణం విభిన్న వాస్తవ మూలాలను కలిగి ఉంటే k విలువను కనుగొనుము.
సాధన.
b2 – 4ac > 0 (మూలాలు విభిన్న వాస్తవ సంఖ్యలు) , .
(5)2 – 4(1) (k) > 0
∴ 25 > 4k ⇒ 4k < 25
⇒ k < [latex]\frac{25}{4}[/latex]
ప్రశ్న 21.
x2 – 4 = 0 మరియు x2 + px – 4 = 0లు ఒకే
మూలాలను కల్గియున్న p విలువ ఎంత ?
(A) 2
(B) o
(C) 4
(D) 1
జవాబు.
(B) o
ప్రశ్న 22.
క్రింది వానిలో వర్గ సమీకరణము
(A) 5 + [latex]\frac{3}{x}[/latex] = x
(B) x2 + [latex]\frac{1}{x^{2}}[/latex] + = [latex]\frac{17}{4}[/latex]
(C) x (x + 3) = 6x + 3
(D) x(2x + 3) = 2x2 – 7
జవాబు.
(C) x (x + 3) = 6x + 3
ప్రశ్న 23.
క్రింది వానిలో వర్గ సమీకరణము
(A) x2 – 6x – 4
(B) (2x + 1) (3x + 2)=0
(C) 7x = 2x2
(D) పైవన్నీ
జవాబు.
(D) పైవన్నీ
ప్రశ్న 24.
క్రింది వానిలో వర్గ సమీకరణము కానిది
(A) x (x – 3) = x2 + 5
(B) x (x + 5) = 2x2 + 4
(C) x2 – √2x – 1 = 0
(D) పైవన్నీ
జవాబు.
(A) x (x – 3) = x2 + 5
ప్రశ్న 25.
వర్గ సమీకరణం యొక్క సాధారణ రూపాన్ని రాయండి.
జవాబు.
ax2 + bx + c = 0, (a ≠ 0)
ప్రశ్న 26.
a యొక్క ఏ విలువకు ax (x2 – 4) + dx = 2x3 + bx2 + 10, b ≠ 0 ఒక వర్గ సమీకరణాన్ని సూచిస్తుంది ?
సాధన.
ax3 – 4ax + dx = 2x3 + bx2 + 10, (b ≠0) |
(a – 2)x3 = bx2 + (d – 4a)x – 10 = 0
వర్గసమీకరణంలో x3 పదం ఉండదు.
∴ a – 2 = 0 ⇒ a = 2
![]()
ప్రశ్న 27.
(m + 1)x3 + 6x2 + 5x = 16 ఒక వర్గ సమీకరణాన్ని సూచిస్తే m విలువ ఎంత ?
సాధన.
వర్గ సమీకరణంలో x3 పదం ఉండదు.
∴ m + 1 = 0 ⇒ m = -1
ప్రశ్న 28.
px2 + qx + r = 0 వర్గ సమీకరణ మూలాలను తెల్పండి.
సాధన.
px2 + qx + r = 0 వర్గ సమీకరణ మూలాలు
[latex]\frac{-\mathrm{q} \pm \sqrt{\mathrm{q}^{2}-4 \mathrm{pr}}}{2 \mathrm{p}}[/latex]
ప్రశ్న 29.
‘రెండు వరుస ధన సంఖ్యల లబ్ధం 132” అయిన ఆ సంఖ్యలను కనుగొనుటకు అవసరమయ్యే వర్గ సమీకరణంను రాయండి.
సాధన.
రెండు వరుస ధన సంఖ్యలు x, x + 1 అనుకొనుము.
∴ x(x + 1) = 132 (లెక్క ప్రకారం లబ్ధం 132)
x2 + x – 132 = 0
ప్రశ్న 30.
“రెండు వరుస బేసి సంఖ్యల లబ్దము 399” అయిన ఆ రెండు సంఖ్యలను కనుగొనుటకు ఉపయోగపడే వర్గ సమీకరణము (x చిన్న బేసి సంఖ్య అయిన)ను కనుగొనుము.
సాధన.
రెండు వరుస బేసి సంఖ్యలలో చిన్న బేసి సంఖ్య x.
∴ రెండవ బేసి సంఖ్య = x + 2 .
వీని లబ్ధం x(x + 2) = 399
కావలసిన వర్గసమీకరణం = x2 + 2x – 399 = 0
ప్రశ్న 31.
“రెండు వరుస సరి సంఖ్యల లబ్దము 120” అయిన ఆ సంఖ్యలను కనుగొనుటకు అవసరమగు వర్గ సమీకరణంను రాబట్టుము.
సాధన.
రెండు, వరుస సరి సంఖ్యలలో చిన్న సరి సంఖ్య x అనుకొనుము.
∴ రెండవ సరి సంఖ్య = x + 2
వీని లబ్ధం x(x + 2) = 120
కావలసిన వర్గసమీకరణం = x2 + 21 – 120 = 0
ప్రశ్న 32.
“ఒక సంఖ్య మరియు ఆ సంఖ్య యొక్క వ్యుత్రమంల మొత్తం [latex]\frac{5}{2}[/latex]” ను సూచించు వర్గ సమీకరణమును కనుగొనుము.
సాధన.
x + [latex]\frac{1}{x}[/latex] = [latex]\frac{5}{2}[/latex] (ఒక సంఖ్య x అనుకొనుము. దాని వృత్రమం [latex]\frac{1}{x}[/latex])
⇒ [latex]\frac{x^{2}+1}{x}[/latex] = [latex]\frac{5}{2}[/latex]
⇒ 2x2 + 2 = 5x
⇒ 2x2 – 5x + 2 = 0
ప్రశ్న 33.
“ఒక సంఖ్య మరియు ఆ సంఖ్య యొక్క వ్యుత్తమంల మొత్తం 2” ను సూచించు వర్గ సమీకరణము
(A) x2 – 2x + 1= 0
(B) x2 + 2x + 1 = 0
(C) x2 + 25 – 1= 0
(D) x2 + 2x + 2 = 0
సాధన.
(A) x2 – 2x + 1= 0
x + [latex]\frac{1}{x}[/latex] = 2
⇒ [latex]\frac{x^{2}+1}{x}[/latex] = 2
⇒ x2 + 1
⇒ 2x = x2 – 2x + 1 = 0
![]()
ప్రశ్న 34.
A = {x/x అనేది (x – 4) (x + 2) = 0 యొక్క మూలము}, B అనే సమితి 2x – 8 యొక్క శూన్య విలువల సమితి అయిన A ∩ Bను కనుగొనుము.
సాధన.
A = {4, – 2}
2x – 8 = 0 ⇒ 2x = 8
⇒ x = 4 శూన్యవిలువ = 4
∴ B = {4}
∴ A ∩ B = {4}
ప్రశ్న 35.
A = {x/x అనేది (x – 4) (x + 2) = 0 యొక్క మూలము}, B అనే సమితి 2x – 8 యొక్క శూన్య విలువల సమితి అయిన A – Bను కనుగొనుము.
సాధన.
A = {4, – 2}
2x – 8 = 0 ⇒ 2x = 8 ⇒ x = 4
శూన్యవిలువ = 4
∴ B = {4}
A – B = {4, – 2} – {4} = {- 2}
ప్రశ్న 36.
క్రింది వానిలో ఏది “రెండు వరుస ధన బేసి సంఖ్యల వర్గాల మొత్తం 290”ను సూచించు వర్గ సమీకరణం ?
(A) x2 + (x + 2)2 = 290
(B) x2 + (x + 2)2 = 2902
(C) x2 – (x + 2)2 = 290
(D) x2 – (x – 2)22 = 2902
జవాబు.
(A) x2 + (x + 2)2 = 290
ప్రశ్న 37.
ఒక సంఖ్య మరియు దాని యొక్క వర్గాల మొత్తం
56నకు సరియగు వర్గ సమీకరణమును రాబట్టుము.
(A) x + 2x2 = 56
(B) 2x + x2 = 56
(C) x + x2 = 56
(D) x – x – 56 = 0
జవాబు.
(C) x + x2 = 56
సాధన.
x + x2 = 56
= x2 + x – 56 = 0.
ప్రశ్న 38.
2x2 – 5x + 3 = 0 యొక్క ఒక మూలము
(A) – 1
(B) 1
(C) 0
(D) 2
జవాబు.
(B) 1 (యత్న-దోష పద్దతి)
సాధన.
2x2 – 5x + 3 = 0
x = – 1 ⇒ 2(- 1)2 – 5 (- 1) + 3
⇒ 2 + 5 + 3 = 10 ≠ 0
x = 1 ⇒ 2(1)2 – 5 (1) + 3
⇒ 2 – 5 + 3 = 0
∴ 1 ఒక మూలము.
![]()
ప్రశ్న 39.
(x – 4) (x + 2) = 0 యొక్క మూలాలు ఏవి ?
సాధన.
(x – 4) (x + 2) = 0
∴ x – 4 = 0 (లేదా) x + 2 = 0
x = 4 (లేదా) x = – 2
∴ మూలాలు’ = – 2, 4.
ప్రశ్న 40.
(2x + 3) (3x – 7) = 0 వర్గ సమీకరణ మూలాలు కనుగొనుము.
సాధన.
(2x + 3) (3x – 7) = 0
= 2x + 3 = 0 (లేదా) 3x-7 = 0
∴ x = [latex]\frac{-3}{2}[/latex] (లేదా) x = [latex]\frac{7}{3}[/latex]
∴ మూలాలు = [latex]\frac{-3}{2}, \frac{7}{3}[/latex]
ప్రశ్న 41.
2x2 – 6x = 0 వర్గ సమీకరణ మూలాలు కనుగొనుము.
సాధన.
2x2 – 6x = 0 ⇒ 2x(x – 3) = 0
∴ 2x = 0 ⇒ x = 0 లేదా x – 3 = 0 ⇒ x = 3
∴ మూలాలు = 0, 3.
ప్రశ్న 42.
x2 – 5x + 6 = 0 యొక్క ఒక మూలం 3 అయిన రెండవ మూలాన్ని కనుగొనుము.
సాధన.
x2 – 5x + 6 = 0
ఒక మూలం α = 3, రెండవ మూలం β అనుకొనుము.
∴ α + β = [latex]\frac{-b}{a}[/latex] ⇒ 3 + β = [latex]\frac{-(-5)}{1}[/latex] = 5
∴ β = 5 – 3 = 2
(లేదా)
మూలాల లబ్ధం αβ = [latex]\frac{c}{a}[/latex]
⇒ 3β = [latex]\frac{6}{1}[/latex] ⇒ β = 2
(లేదా)
x2 – 3x – 2x + 6 = 0
⇒ x(x – 3) – 2 (x – 3) = 0
⇒ (x – 3) (x – 2) = 0
∴ మూలాలు α = 3, β = 2.
ప్రశ్న 43.
x2 + 6x + 5 = 0 యొక్క మూలాలు α మరియు β అయిన α + β విలువ ఎంత ?
సాధన.
α + β = [latex]\frac{-b}{a}[/latex] = [latex]\frac{-6}{1}[/latex] = – 6
ప్రశ్న 44.
x2 – 5x + 6 = 0 యొక్క మూలాలు α మరియు β, α > β అయిన α – β విలువను కనుగొనుము.
సాధన.
x2 – 5x + 6 = 0 ,
x2 – 3x – 2x + 6 = 0
⇒ x(x – 3) – 2 (x – 3) = 0
⇒ (x – 3) (x – 2) = 0
∴ మూలాలు α = 3, β = 2.
∴ α – β = 3 – 2 = 1.
(లేదా) .
α + β = 5, αβ = 6
∴ (α – β)2 = (α + β)2 – 4αβ
= 52 – 4(6) = 25 – 24 = 1
∴ (α – β)2 = 1 ⇒ α – β = √1 = 1
ప్రశ్న 45.
x2 – 3x- 10 = 0 యొక్క మూలాలు α, β అయిన – α2 + β2 విలువను గణించండి.
(A) 21
(B) 25
(C) 29
(D) 10
సాధన.
(C) 29
x2 – 3x – 10 = 0 యొక్క మూలాలు α, β. ,
∴ α + β = [latex]\frac{-b}{a}[/latex] = 3, αβ = [latex]\frac{c}{a}[/latex] = – 10
∴ (α + β)2 = α2 + β2 + 2αβ
⇒ (3)2 = α2 + β2 + 2(-10)
⇒ 9 + 20 = α2 + β2
∴ α2 + β2 = 29
(లేదా)
x2 – 3x – 10 = 0
x2 – 5x + 2x – 10 = 0
⇒ x(x – 5) + 2(x – 5) = 0
⇒ (x – 5) (x + 2) = 0
α = 5, β = -2.
∴ α2 + β2 = (5)2 + (-2)2
= 25 + 4 = 29
![]()
ప్రశ్న 46.
x2 – 3x – 4 = 0 యొక్క మూలాలు α, β అయిన α3 + β3 విలువను కనుగొనుము.
(A) 64
(B) 63
(C) – 1
(D) 17
జవాబు.
(B) 63
సాధన.
x2 – 3x – 4 = 0 యొక్క మూలాలు α, β.
∴ α + β = 3, αβ = – 4
∴ α3 + β3 = (α + β)3 – 3αβ(α + β)
⇒ (3)3 – 3(-4) (3) = 27 + 36 = 63
ప్రశ్న 47.
x2 + 4x + 4 = 0వర్గ సమీకరణ మూలాలు p, q అయిన క్రింది వానిలో ఏది సత్యం ?
(A) pq = 4
(B) p = – 2, q = -2
(c) p + q = – 4
(D) పైవన్నీ
జవాబు.
(D) పైవన్నీ
ప్రశ్న 48.
x2 – 6x + 8 = 0 వర్గ సమీకరణ మూలాలు p, q అయిన p ∙ q విలువ ఎంత ?
సాధన.
మూలాల లబ్ధం pq = [latex]\frac{c}{a}[/latex] = [latex]\frac{8}{1}[/latex] = 8
ప్రశ్న 49.
x2 + 2kx + 16 = 0 కు 4 ఒక మూలము అయితే k విలువను కనుగొనుము.
సాదన.
x2 + 2kx + 16 = 0కు 4 ఒక మూలము.
(4)2 + 8k + 16 = 0
⇒ 8k + 32 = 0 ⇒ k = [latex]\frac{- 32}{8}[/latex] = – 4
ప్రశ్న 50.
x2 + 2√2x – k = 0 కు /Z ఒక మూలము అయితే k విలువను కనుగొనుము.
సాధన.
(√2)2 + 2√2(√2) – k = 0
⇒ 2 + 4 – k = 0 ⇒ k = 6
ప్రశ్న 51.
ax2 + ax + 8 = 0 మరియు x2 + x + c = 0 వర్గ సమీకరణాలకు x = 1 ఒక ఉమ్మడి మూలం అయిన ac = 8 అని చూపుము.
సాధన.
ax2 + ax + 8 = 0 మరియు x2 + x + c = 0కు
1 ఒక ఉమ్మడి మూలము.
∴ a(1)2 + a(1) + 8 = 0 మరియు
(1)2 + 1 + c ⇒ 0 = c = -2
2a = – 8 ⇒ a = -4
∴ ac = (- 4) (- 2) = 8
![]()
ప్రశ్న 52.
a యొక్క ఏ విలువకైనా (a + 2)x2 – ax – 2 = 0 కు క్రింది వానిలో ఏది ఒక మూలం ?
(A) 1
(B) – 1
(C) 0
(D) 2
జవాబు.
(A) 1
సాధన.
గుణకాల మొత్తం (a + 2) + (- a) + (- 2) = 0
కావున 1 ఒక శూన్యం అవుతుంది.
(లేదా )
యత్న-దోష పద్దతిలో సాధించాలి.
1 ఒక శూన్యం అనుకొనుము.
(a + 2)(1)2 – a(1) – 2
= a + 2 – a – 2 ≠ 0
కావున 1 ఒక మూలము.
– 1 ఒక శూన్యం అనుకొనుము.
(a + 2) (- 1)2 – a (- 1) – 2
![]()
∴ – 1 మూలము కాదు.
ఇదే విధంగా 0, 2 కు కూడా సరిచూడగలరు.
ప్రశ్న 53.
ax2 + bx + c = 0 వర్గ సమీకరణ మూలాలు సమానం అయిన c = [latex]\frac{b^{2}}{4 a}[/latex] అని చూపుము. .
సాధన.
b2 – 4ac = 0 ⇒ 4ac = b2 ⇒ c = [latex]\frac{b^{2}}{4 a}[/latex]
ప్రశ్న 54.
ax2 + bx + c = 0 వర్గ సమీకరణ మూలాలు సమానం అయిన
(A) b2 – 4ac > 0
(B) b2 – 4ac < 0
(C) b2 – 4ac = 0
(D) పైవి ఏవీకాదు
జవాబు..
(C) b2 – 4ac = 0
ప్రశ్న 55.
ax2 + bx + c = 0 వర్గ సమీకరణ విచక్షణిని రాయండి.
జవాబు.
b2 – 4ac
![]()
ప్రశ్న 56.
ax2 + bx + c = 0 వర్గ సమీకరణ మూలాలు సమానమైనచో సమాన మూలంను తెల్పండి.
జవాబు.
[latex]\frac{-b}{2 a}[/latex]
ప్రశ్న 57.
x2 + px – q = 0 వర్గసమీకరణ విచక్షణిని రాయండి.
సాధన.
p2 – 4(1) (-q) = p2 + 4q
ప్రశ్న 58.
ఒక లంబకోణ త్రిభుజం యొక్క ఒక భుజం మరొక భుజం కన్నా 3 సెం.మీ. ఎక్కువ మరియు కర్ణము 15 సెం.మీ., చిన్న భుజం x సెం.మీ. అయిన క్రింది ఏ వర్గ సమీకరణాన్ని తృప్తి పరుస్తుంది ?
(A) 3x2 + 6x – 108 = 0
(B) x2 + 6x – 108 = 0
(C) x2 + 3x – 108 = 0
(D) 2x2 + 3x + 108 = 0
జ.
(C) x2 + 3x – 108 = 0
సాధన.
చిన్న భుజం X అనుకొనుము.
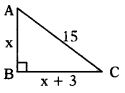
AB2 + BC2 = AC2
x2 + (x + 3)2 = 152
x2 + x2 + 6x + 9 = 225
2x2 + 6x + 9 – 225 = 0
2x2 + 6x – 216 = 0
2(x2 + 3x – 108) = 0
∴ x2 + 3x – 108 = 0
ప్రశ్న 59.
మొత్తము 27, లబ్దము 180 అయ్యే విధంగా రెండు సంఖ్యలను కనుగొనుటకు ఉపయోగపడే వర్గ సమీకరణంను కనుగొనుము.
సాధన.
రెండు సంఖ్యలు x, 27 – x అనుకొనుము.
x(27 – x) = 180 ⇒ 27x – x2 = 180
∴ x2 – 27x + 180 = 0
(లేదా)
ఆ రెండు సంఖ్యలు α, β అనుకొనుము.
– α + β = 27, αβ = 180
∴ వర్గ సమీకరణం = x2 – (α + β)x + αβ = 0
x2 – 27x + 180 = 0
ప్రశ్న 60.
ఒక త్రిభుజం యొక్క భూమి, దాని ఎత్తు కంటే 4 సెం.మీ. ఎక్కువ. ఈ త్రిభుజ వైశాల్యము 48 చ.సెం.మీ. త్రిభుజ ఎత్తును లెక్కించుటకు సరియగు వర్గ సమీకరణమును ఎత్తు X సెం.మీ. అయిన సందర్భంలో రాయండి.
సాధన.
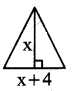
త్రిభుజ వైశాల్యం = [latex]\frac{1}{2}[/latex] bh = 48
⇒ [latex]\frac{1}{2}[/latex](x + 4)x = 48
∴ x2 + 4x = 96 ⇒ x2 + 4x – 96 = 0
![]()
ప్రశ్న 61.
2x2 – 8x + p = 0 వర్గ సమీకరణం వాస్తవ మూలాలను కలిగి ఉండటానికి అవసరమయ్యే p యొక్క గరిష్ఠ విలువ ఎంత ?
సాధన.
2x2 – 8x + p = 0 యొక్క మూలాలు వాస్తవ మూలాలను కలిగి ఉంటే b2 – 4ac ≥ 0.
∴ (-8)2 – 4(2)p ≥ 20
⇒ 64 ≥ 8p ≥ 0
⇒ 64 ≥ 8p ⇒ 8 ≥ p ⇒ p ≤ 8
∴ p గరిష్ట విలువ = 8.
ప్రశ్న 62.
3x2 + 6x + k = 0కు వాస్తవ విభిన్న మూలాలుంటే k < 3 అని చూపుము.
సాధన.
3x2 + 6x + k = 0కు వాస్తవ విభిన్న మూలాలుంటే
b2 – 4ac > 0 ⇒ (6)2 – 4(3)k > 0
∴ 36 – 12k > 0 ⇒ 12k < 36
⇒ k < [latex]\frac{36}{12}[/latex] = 3
∴ k < 3.
ప్రశ్న 63.
x2 + kx + 25 = 0 వర్గ సమీకరణ మూలాలు వాస్తవాలైతే k2 ≥ 100 అని చూపుము.
సాధన.
x2 + kx + 25 = 0 మూలాలు వాస్తవ మూలాలైతే
k2 – 4(1)(25) ≥ 0
⇒ k2 – 100 ≥ 0 ⇒ k2 ≥ 100
ప్రశ్న 64.
kx2 – 6x + 9 = 0 యొక్క మూలాలు వాస్తవాలు కాకపోతే k విలువను కనుగొనుము.
సాధన.
kx2 – 6x + 9 = 0 యొక్క మూలాలు వాస్తవాలు కాకపోతే
(- 6)2 – 4(k)(9) < 0 (∵ b2 – 4ac < 0)
36 – 36k < 0 36k > 36 ⇒ k > [latex]\frac{36}{36}[/latex] = 1
∴ k > 1
ప్రశ్న 65.
3x2 + 6x + k = 0 యొక్క మూలాలు సంకీర్ణ సంఖ్యలు అయితే k > 3 అని చూపుము.
సాధన.
3x2 + 6x + k = 0 యొక్క మూలాలు సంకీర్ణ
సంఖ్యలు అనగా వాస్తవ సంఖ్యలు కావు.
∴ (6)2 – 4(3)k < 0 (∵ b2 – 4ac < 0)
36 – 12k < 0 ⇒ 12k > 36 ⇒ k > 3 .
ప్రశ్న 66.
2x2 + kx + 3 = 0 వర్గ సమీకరణానికి రెండు సమాన వాస్తవ మూలాలుంటే k విలువ ఎంత ?
సాధన.
2x2 + kx + 3 = 0 మూలాలు సమానాలు .
∴ k2 – 4(2) (3) = 0 (∵ b2 – 4ac = 0)
k2 = 24 = k ⇒ √24
![]()
ప్రశ్న 67.
k యొక్క ఏ విలువకు kx (x – 2) + 6 = 0 వర్గ సమీకరణ మూలాలు సమాన వాస్తవ సంఖ్యలు అవుతాయి ?
సాధన.
kx2 – 2kx + 6 = 0 యొక్క మూలాలు సమానాలు.
∴ (- 2k)2 – 4(k) (6) = 0
⇒ 4k2 – 24k = 0 ⇒ 4k (k – 6) = 0
k ≠ 0, ∴ k – 6 = 0 ⇒ k = 6 .
ప్రశ్న 68.
x22 – k2 = 0 యొక్క ఒక మూలం – 3 అయిన మరొక మూలంను కనుగొనుము.
సాధన.
x2 – k2 = 0 యొక్క ఒక మూలము α = – 3, β = ?
α + β = [latex]\frac{-b}{a}[/latex] = 0 ⇒ – 3 + β = 0, β = 3
(లేదా)
– 3 ఒక మూలము.
∴ (-3)2 – k2 = 0 ⇒ k2 = 9
⇒ k = √9 = ± 3,
రెండవ మూలము 3.
ప్రశ్న 69.
క్రింది వానిలో మూలాలు సమానంగా గల వర్గ సమీకరణము ఏది ?
(A) x2 + 4x + 4 = 0
(B) x2 – 4x + 4 = 0
(C) A మరియు B
(D) ఏదీకాదు
జవాబు.
(C) A మరియు B
ప్రశ్న 70.
విభిన్న వాస్తవ మూలాలు కలిగిన వర్గ సమీకరణం ఒకదానిని రాయండి.
సాధన.
(ఏవైనా రెండు వాస్తవ సంఖ్యలు మూలాలుగా గల వర్గ సమీకరణం కనుగొనాలి)
2, 3 మూలాలుగా గల వర్గసమీకరణం కనుగొందాం.
(x – 2) (x – 3) = 0
x2 – 5x + 6 = 0
ప్రశ్న 71.
2x2 – 3x + 5 = 0 వర్గ సమీకరణ మూలాల స్వభావాన్ని రాయండి.
సాధన.
విచక్షణి b2 – 4ac = (- 3)2 – 4(2)(5)
= 9 – 40 = – 31 < 0
కావున, మూలాలు వాస్తవ సంఖ్యలు కావు.
![]()
ప్రశ్న 72.
3x2 – 4√3x + 4 = 0 వర్గ సమీకరణ మూలాలు సమాన వాస్తవ సంఖ్యలని చూపండి.
సాధన.
b2 – 4ac = (- 4√3)2 – 4(3)4
= 48 – 48 = 0
కావున, మూలాలు సమాన వాస్తవ సంఖ్యలు.
ప్రశ్న 73.
2x2 + 6x + 3 = 0 వర్గ సమీకరణ మూలాల స్వభావాన్ని రాయండి.
సాధన.
b2 – 4ac = (6)2 – 4(2)(3)
= 36 – 24 = 12 > 0 0
∴ మూలాలు అసమాన వాస్తవ సంఖ్యలు.
ప్రశ్న 74.
x2_5x + 4 = 0 యొక్క మూలాలు α, β మరియు α, k, P లు గుణశ్రేణిలో ఉంటే k విలువ ఎంత ?
సాధన.
x2 – 5x + 4 = 0 యొక్క మూలాలు α, β.
∴ α + β = 5, αβ = 4
α, k, β లు గుణశ్రేణిలో కలవు.
∴ [latex]\frac{\mathrm{k}}{\alpha}[/latex] = [latex]\frac{\beta}{\mathrm{k}}[/latex] ⇒ k2 = αβ = 4
∴ k = √4 = ± 2.
ప్రశ్న 75.
ax2 + bx + c = 0 వర్గ సమీకరణ మూలాలు : సమాన వాస్తవ సంఖ్యలు కావడానికి గల నియమాన్ని రాయండి.
జవాబు.
b2 – 4ac = 0
ప్రశ్న 76.
ax2 + bx + c = 0 వర్గసమీకరణ విచక్షణి b2 – 4ac > 0 అయితే మూలాలు గూర్చి నీవు ఏమి చెప్పగలవు ?
జవాబు.
మూలాలు విభిన్న వాస్తవ సంఖ్యలు.
ప్రశ్న 77.
వర్గ సమీకరణ విచక్షణి b2 – 4ac < 0 అయిన మూలాల స్వభావమును తెల్పండి.
(A) వాస్తవ సమాన సంఖ్యలు
(B) వాస్తవ విభిన్నాలు
(C) వాస్తవ సంఖ్యలు కావు
(D) మూలాలు శూన్యాలు
జవాబు.
(C) వాస్తవ సంఖ్యలు కావు (మూలాలు వాస్తవ సంఖ్యలు కావు).
ప్రశ్న 78.
ax2 + bx + c = 0 వర్గ సమీకరణ గ్రాను b2 – 4ac < 0 అయినప్పుడు చిత్తు పటంలో చూపండి.
జవాబు.
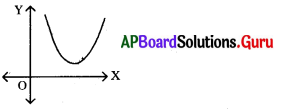
ప్రశ్న 79.

(A) b2 – 4ac = 0
(B) b2 – 4ac < 0
(C) b2 – 4ac0
(D) b2 – 4ac > 0
జవాబు.
(D) b2 – 4ac > 0
![]()
ప్రశ్న 80.
ax2 + bx + c = 0 యొక్క మూలాలు సంకీర్ణ సంఖ్యలు (వాస్తవ సంఖ్యలు కాకపోతే) అయితే ఆ వర్గ సమీకరణ గ్రాను చిత్తుపటంలో చూపండి.
జవాబు.
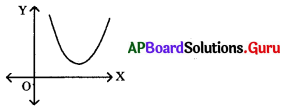
ప్రశ్న 81.
b24ac > 0 అయిన ax2 + bx + c = 0వర్గ సమీకరణ గ్రాఫ్ క్రింది వానిలో ఏది కాదు ?
(A)
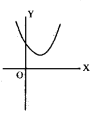
(B)
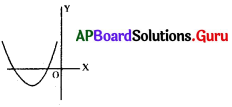
(c)
(D) పైవన్నీ
జవాబు.

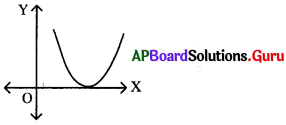
ప్రశ్న 82.
b2 – 4ac = 0 అయినప్పుడు 2 + bx + c = 0 వర్గ సమీకరణ (ను చిత్తు పటంగా గీయండి.
జవాబు.
ప్రశ్న 83.
x2 + bx + c = 0 వర్గ సమీకరణ గ్రాఫ్ కు చెందిన క్రింది వాటిలో ఏది అసత్యము ?
(A) b2 – 4ac > 0 అయిన గ్రాఫ్ X – అక్షాన్ని రెండు బిందువుల వద్ద ఖండిస్తుంది.
(B) B2 – 4ac < 0 అయిన గ్రాఫ్ X – అక్షాన్ని ఖండించదు.
(C) b2 – 4ac = 0.అయిన గ్రాఫ్ X – అక్షాన్ని రెండు బిందువుల వద్ద ఖండిస్తుంది.
(D) పైవన్నీ
జవాబు.
(C) b2 – 4ac = 0.అయిన గ్రాఫ్ X – అక్షాన్ని రెండు బిందువుల వద్ద ఖండిస్తుంది.
ప్రశ్న 84.
విభాగం-I లోని విచక్షణి విలువకు, విభాగం-IIలోని మూలాల స్వభావానికి జత చేయండి.

(A) i-b, ii-a, iii-c
(B) i-c, ii-a, iii-b
(C) i-c, ii-b, iii-a
(D) i-b, ii-c, iii-a
జవాబు.
(B) i-c, ii-a, iii-b
ప్రశ్న 85.
√3x2 – 6x + 12√3 = 0 వర్గ సమీకరణ విచక్షణిని కనుగొనుము.
సాధన.
విచక్షణి b2 – 4ac
= (- 6)2 – 4(√3)12√3
= 36 – 144
= – 108
![]()
ప్రశ్న 86.
x2 – 3x – k = 0 వర్గ సమీకరణ విచక్షణి 25 అయిన ఓ విలువ ఎంత ?
సాధన.
b2 – 4ac = 25
⇒ (-3)2 – 4(1) (- k) = 25
⇒ 9 + 4k = 25
⇒ 4k = 25 – 9
∴ 4k = 16 ⇒ k = 4
ప్రశ్న 87.
3x2 – 5x + 2 = 0 యొక్క ఒక మూలము 1 అయిన రెండవ మూలం ఎంత ?
సాధన.
మూలాల మొత్తం α + β = [latex]\frac{-b}{a}[/latex] = [latex]\frac{-(-5)}{3}[/latex]
∴ 1 + β = [latex]\frac{5}{3}[/latex] (∵ ఒక మూలం 1)
రెండవ మూలం β = [latex]\frac{5}{3}[/latex] – 1 = [latex]\frac{2}{3}[/latex]
(లేదా) ..
మూలాల లబ్ధం αβ = [latex]\frac{c}{a}[/latex] = [latex]\frac{2}{3}[/latex]
(1) β = [latex]\frac{2}{3}[/latex]
∴ β = [latex]\frac{2}{3}[/latex]
ప్రశ్న 88.
విభాగం-Iలోని విచక్షణి విలువకు, విభాగం-II లోని గ్రాఫ్ రూపానికి జత చేయండి.
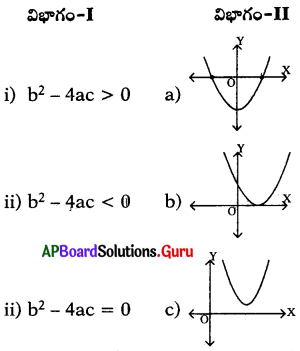
(A) i-a, ii-c, iii-b
(B) i-a, ii-b, iii-c
(C) i-b, ii-a, iii-c
(D) i-b, ii-c, iii-a
జవాబు.
(A) i-a, ii-c, iii-b
ప్రశ్న 89.
వాదన I : x2 – 6x + 9 = 0 వర్గసమీకరణ మూలాలు సమాన వాస్తవ సంఖ్యలు.
వివరణ II : ax2 + bx + c = 0 యొక్క విచక్షణి b2 – 4ac = 0 అయిన మూలాలు. సమాన వాస్తవ సంఖ్యలు. (A) I అసత్యం , II సత్యం , I & II సరైన వివరణ
(B) I సత్యం, II సత్యం, I & II సరైన వివరణ కాదు
(C) I సత్యం, II సత్యం , I & II సరైన వివరణ
(D) I అసత్యం, II అసత్యం
జవాబు.
(D) I అసత్యం, II అసత్యం
ప్రశ్న 90.
x2 – x – 20 = 0 సమీకరణానికి చెందిన క్రింది ఏది అసత్యం ?
(A) వేర్వేరు వాస్తవ మూలాలను కలిగి ఉంటుంది
(B) – 4 మరియు 5 లు మూలాలు
(C) వాస్తవ సమాన మూలాలను కలిగి ఉంటుంది
(D) A మరియు B
జవాబు.
D
![]()
ప్రశ్న 91.
a = 1 అయిన ax2 + 2x + a = 0 కు గల : మూలాలు సమానం అని చూపుము.
సాధన.
b2 – 4ac = (2)2 – 4(a)(a) = 4 – 4a2,
a = 1 అయితే 4 – 4a2 = 4 – 4(1)2 = 0
a = 1 అయినప్పుడు b2 – 4ac = 0 కావున మూలాలు సమానము.
(లేదా)
a = 1 అయిన ఇచ్చిన వర్గసమీకరణం
= x2 + 2x + 1 = 0
∴ b2 – 4ac = (2)2 – 4(1) (1) = 0. కావున మూలాలు సమానం.
ప్రశ్న 92.
b2 – 4ac > 0 అయిన సందర్భంలో వర్గ సమీకరణం యొక్క రేఖాచిత్రం చిత్తుపటం గీయండి.
సాధన.
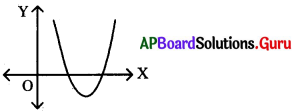
ప్రశ్న 93.
x2 + 6x + λ = 0 ఖచ్చిత వర్గం అయిన 7 విలువ ఎంత ?
సాధన.
x2 + 6x + λ = 0 ఖచ్చిత వర్గం అయితే
(a + b)2 = a2 + 2ab + b2 రూపంలో ఉంటుంది.
∴ x2 + 2 ∙ 3 ∙ x + λ = 0
ఇక్కడ, a = x, b = 3, λ = b2
λ = (3)2 = 9
(లేదా)
x2 + 6x + λ = 0 ఖచ్చిత వర్గం అయితే మూలాలు ‘సమానాలు.
∴ b2 – 4ac = 0
⇒ (6)2 – 4(1)λ = 0
⇒ 36 – 4λ = 0 ⇒ 36 = 4λ.
∴ λ = 9
ప్రశ్న 94.
3, 3 మూలాలుగా గల వర్గ సమీకరణం యొక్క రేఖాచిత్రం చిత్తుపటం గీయండి.
జవాబు.
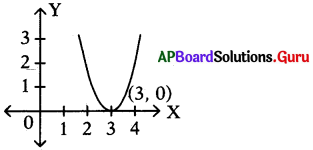
ప్రశ్న 95.
x2 + 2x + (λ2 + 1) = 0 వర్గ సమీకరణ మూలాలు సమానం అయితే λ విలువను కనుగొనుము.
సాధన.
b2 – 4ac = 0
⇒ (2)2 – 4(1)(λ2 + 1) = 0
⇒ 4 – 4λ2 – 4 = 0
⇒ 4λ2 = 0
∴ λ2 = 0 ⇒ λ = 0
ప్రశ్న 96.
b2 – 4ac< 0 అయినపుడు ax2 + bx + c = 0 మరియు a < 0 అయిన సందర్భంలో వర్గ సమీకరణం యొక్క గ్రాఫ్ (రేఖాచిత్రం)ను గీయండి..
జవాబు.
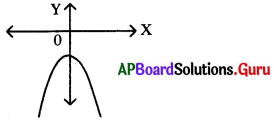
![]()
ప్రశ్న 97.
(2x + 3)2 = 0 వర్గ సమీకరణం యొక్క విచక్షణిని కనుగొనుము.
సాధన.
0 (∵ ఇచ్చిన వర్గసమీకరణం (a + b)2 = 0 రూపంలో కలదు. కావున మూలాలు సమానం. కావున విచక్షణి ‘0’).
(లేదా )
(2x + 3)2 = 4x2 + 12x + 9
b2 – 4ac = (12)2 – 4(4)(9)
= 144 – 144 = 0
ప్రశ్న 98.
3x2 + 2√5x – 5 = 0 వర్గ సమీకరణం యొక్క విచక్షణిని కనుగొనుము.
సాధన.
3x2 + 2√5x – 5 = 0
విచక్షణి b2 – 4ac = (2√5)2 – 4(3)(- 5)
= 20 + 60 = 80
ప్రశ్న 99.
(3x – 2)2 = – 2 (3x – 2)2 యొక్క మూలాలు
(A) [latex]\frac{-2}{3}, \frac{-2}{3}[/latex]
(B) [latex]\frac{2}{3}, \frac{2}{3}[/latex]
(C) [latex]\frac{3}{2}, \frac{3}{2}[/latex]
(D) [latex]\frac{-2}{3}, \frac{2}{3}[/latex]
జవాబు.
(B) [latex]\frac{2}{3}, \frac{2}{3}[/latex]
సాధన.
(3x – 2)2 = -2 (3x – 2)2
⇒ (3x – 2)2 + 2(3x – 2)2 = 0
⇒ 3(3x – 2)2 = 0
∴ (3x – 2)2 = 0 ⇒ (3x – 2) (3x – 2) = 0 2
∴ మూలాలు [latex]\frac{2}{3}, \frac{2}{3}[/latex]
ప్రశ్న 100.
3(x – 4)2 = (x – 4)2 + 8 యొక్క ఒక మూలం ‘6’ అవుతుందని చూపండి.
సాధన.
3(x – 4)2 = (x – 4)2 + 8
x = 6 అయిన 3(6 – 4 )2 = (6 – 4)2 + 8
12 = 4 + 8 ⇒ 12 = 12
కావున, 6 ఒక శూన్యం అవుతుంది.
ప్రశ్న 101.
వర్గ బహుపది ax2 + bx + c యొక్క శూన్య విలువలు 2, -3 అయిన ax2 + bx + c = 0 – యొక్క మూలాలను రాయండి.
సాధన.
(2, – 3) (∵ ax2 + bx + c యొక్క శూన్యాలు
ax2 + by + c = 0 క్క మూలాలు అవుతాయి.)
ప్రశ్న 102.
(x + 2)2 – 9 = 0 వర్గ సమీకరణ మూలాలను కనుగొనుము.
సాధన.
(x + 2)2 – 9 = 0 ⇒ (x + 2)2 = 9
x + 2 = √9 = ± 3.
∴ x + 2 = 3 ⇒ x = 1
x + 2 = – 3 ⇒ x = – 5
∴ మూలాలు = 1, – 5.
ప్రశ్న 103.
x2 – 4x + 2 = 0 వర్గ సమీకరణ మూలాలను కనుగొనుము.
సాధన.
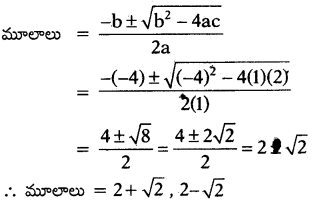
![]()
ప్రశ్న 104.
“రెండు సంఖ్యల మొత్తం 15, వాని వర్గాల మొత్తం 117” అయిన ఆ సంఖ్యలను కనుగొనుటకు అవసరమగు వర్గసమీకరణాన్ని రాబట్టుము.
సాధన.
ఆ సంఖ్యలు α, β అనుకొంటే,
α + β = 15, αβ = 117.
వర్గ సమీకరణం = x2 – (α + β)x + αβ = 0
∴ కావలసిన వర్గసమీకరణం x2 – 15x + 117 = 0.
ప్రశ్న 105.
ax2 + bx + c = 0 యొక్క సాధనకు ఉపయోగించే వర్గసూత్రాన్ని రాయండి.
(లేదా)
ax2 + bx + c = 0 వర్గ సమీకరణ సాధన (మూలాలను) రాయండి.
సాధన.
[latex]\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}[/latex]
ప్రశ్న 106.
“3x2 – 4√5x + 4 = 0 వర్గ సమీకరణ మూలాలు సమాన వాస్తవ సంఖ్యలు”. ఇచ్చిన వర్గ సమీకరణ – మూలాలను తెల్పండి.
సాధన.
సమాన వాస్తవ మూలాలు = [latex]\frac{-b}{2 a}, \frac{-b}{2 a}[/latex]
= [latex]\frac{-(-4 \sqrt{3})}{6}[/latex] = [latex]\frac{2}{\sqrt{3}}, \frac{2}{\sqrt{3}}[/latex]
ప్రశ్న 107.
ప్రవచనం-I: ax2 + bx + c = 0 యొక్క విచక్షణి b2 – 4ac > 0 అయిన మూలాలు సమాన వాస్తవ సంఖ్యలు.
ప్రవచనం-II: ax2 + bx + c = 0 యొక్క విచక్షణి b2 – 4ac < 0 అయిన మూలాలు అసమాన ‘వాస్తవ సంఖ్యలు.
(A) I, II లు రెండూ సత్యము
(B) I సత్యం, II అసత్యం
(C) I సత్యం, II అసత్యం
(D) I మరియు II లు రెండూ అసత్యం
జవాబు.
(D) I మరియు II లు రెండూ అసత్యం
ప్రశ్న 108.
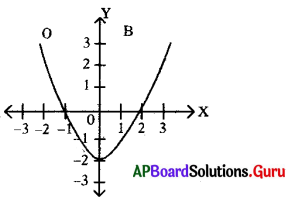
పై పటంలోని గ్రాను సూచించే వర్గ సమీకరణ మూలాలు రాయండి.
సాధన. మూలాలు – 1 మరియు 2.
ప్రశ్న 109.
2x2 – 2√2x + k= 0 వర్గ సమీకరణ మూలాలు సమానాలు అయినపుడు k విలువను కనుగొనుము.
సాధన.
b2 – 4ac = 0 (∵ మూలాలు సమానం)
(- 2√2)2 – 4(2)k = 0
⇒ 8 – 8k = 0 ⇒ 8 = 8k
∴ k = 1.
ప్రశ్న 110.
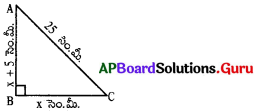
పై లంబకోణ త్రిభుజం ABC యొక్క మిగిలిన రెండు భుజాలను కనుగొనుటకు అవసరమైన వర్గ సమీకరణమును రాబట్టుము.
సాధన.
(x + 5)2 + x2 = 252 (∵ ∠B = 90°
= AC2 = AB + BC2)
x2 + 10x + 25 + x2 = 625
2x2 + 10x – 600 = 0.
ప్రశ్న 111.
2x2 – 2√2x + 1 = 0 వర్గ సమీకరణ మూలాలు సమానం అయితే ఆ మూలాలను కనుగొనుము.
సాధన.
సమాన మూలాలు [latex]\frac{-b}{2 a}, \frac{-b}{2 a}[/latex] = [latex]\frac{2 \sqrt{2}}{4}[/latex]
= [latex]\frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2}[/latex] = [latex]\frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}}[/latex]
(లేదా)
మూలాలు సమానం కావున b2 – 4ac = 0
∴ మూలాలు = [latex]\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}[/latex]
= [latex]\frac{-(-2 \sqrt{2}) \pm 0}{2(2)}[/latex]
= [latex]\frac{2 \sqrt{2}}{4}[/latex]
= [latex]\frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}}[/latex]
![]()
ప్రశ్న 112.
(2x + 1)3 = px3 + 5 ఒక వర్గ సమీకరణం అయితే p = ……………
(A) 8
(B) 4
(C) 2
(D) 0
జ.
(A) 8
సాధన.
p = 8 (L.H.S. మరియు R.H.S. లలో 3 గుణకం సమానం కావాలి)
⇒(2x + 1)3 = px3 + 5
⇒ (2x)3 + 13+ 3(2x)(1)(2x + 1) = px3 + 5
⇒ 8x3 + 13 + 12x2 + 6x = px3 + 5
∴ p = 8
[∵ (a + b)3 = a3 + B3 + 3ab (a + b)]
ప్రశ్న 113.
ఒక వర్గ సమీకరణానికి గల గరిష్ఠ మూలాల సంఖ్య ఎంత ?
జవాబు.
2
ప్రశ్న 114.
స్థిరపదం లోపించిన వర్గ సమీకరణమునకు ఎల్లప్పుడు ‘0’ ఒక మూలం అని చూపుము.
సాధన.
ax2 + bx + c = 0 లో స్థిరపదం లోపిస్తే అది
ax2 + bx = 0 ⇒ x(ax + b) = 0
x = 0 (లేదా) ax + b = 0
∴ ‘0’ ఒక మూలము.
(లేదా)
మూలాల లబ్ధం αβ = [latex]\frac{c}{\mathrm{a}}[/latex] = [latex]\frac{0}{\mathrm{a}}[/latex] = 0 (∵ c = 0)
∴ α = 0 (లేదా) β = 0
కావున ‘0’ ఒక మూలము.
ప్రశ్న 115.
x (x + 4) = 12 కు వర్గ సమీకరణ ప్రామాణిక రూపం తెల్పండి.
జవాబు.
x2 + 4x – 12 = 0
ప్రశ్న 116.
(2x – 1) (2x + 1) = 0 వర్గ సమీకరణ మూలాలు రాయండి.
జవాబు.
మూలాలు [latex]\frac{1}{2}[/latex], -[latex]\frac{1}{2}[/latex].
ప్రశ్న 117.
క్రింది ఏ సందర్భంలో వర్గ సమీకరణం యొక్క మూలాలు వాస్తవ సంఖ్యలు అవుతాయి ?
(A) b2 – 4ac > 0 ‘
(B) B2 – 4ac = 0 i
(C) b2 – 4ac < 0
(D) A మరియు B
జవాబు.
(D) A మరియు B
ప్రశ్న 118.
ఈ క్రింది గ్రాఫ్ సూచించే వర్గ సమీకరణము యొక్క మూలాలు
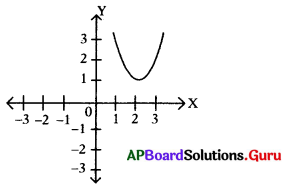
(A),సమాన వాస్తవసంఖ్యలు
(B) విభిన్న వాస్తవసంఖ్యలు
(C) వాస్తవసంఖ్యలు కాదు
(D) ఏమీ చెప్పలేము
జవాబు.
(C) వాస్తవసంఖ్యలు కాదు
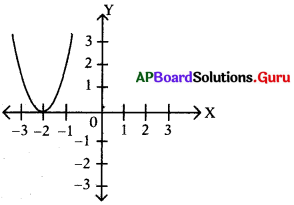
ఈ క్రింది పటాన్ని పరిశీలించి, 119, 120 ప్రశ్నలకు సమాధానాలు రాయండి.
![]()
ప్రశ్న 119.
గ్రాఫ్ సూచించే వర్గ సమీకరణమును రాయండి.
సాధన.
(x + 2)2 = 0 = x2 + 2x + 4 = 0
ప్రశ్న 120.
గ్రాఫ్ సూచించే వర్గ సమీకరణ మూలములను తెల్పండి.
జవాబు.
-2, -2 (లేదా) – 2
ప్రశ్న 121.
ఒక వర్గ సమీకరణ గ్రాఫ్ X – అక్షాన్ని (2, 0) బిందువు వద్ద స్పర్శిస్తుంటే ఆ వర్గసమీకరణ ఒక మూలంను ” తెల్పండి.
జవాబు.
2.
ప్రశ్న 122.
ఓ యొక్క ఏ విలువకు 3x2 – 2x + k= 0 యొక్క విచక్షణి శూన్యం అవుతుంది ?
సాధన.
b2 – 4ac = 0 = (- 2)2 – 4(3)(k) = 0
⇒ 4 – 12k = 0
⇒ 12k = 4
⇒ k = [latex]\frac{1}{3}[/latex]
ప్రశ్న 123.
నిత్య జీవితంలో వర్గ సమీకరణాలను ఉపయోగించే ఒక సందర్భాన్ని తెల్పండి.
జవాబు.
రాకెట్ ను ప్రయోగించే సందర్భంలో, రాకెట్ గమన మార్గాన్ని నిర్వచించడంలో వర్గ సమీకరణాన్ని ఉపయోగిస్తారు.
(లేదా)
డిష్ యాంటెనాల తయారీలో / కంటి అద్దాల తయారీలో వర్గసమీకరణంను ఉపయోగిస్తారు.
ప్రశ్న 124.
x2 – 3x + 2 = 0 వర్గ సమీకరణ మూలాల మొత్తం ఎంత ?
సాధన.
మూలాల మొత్తం = [latex]\frac{-b}{a}[/latex] = [latex]\frac{-(-3)}{1}[/latex] = 3
ప్రశ్న 125.
x2 + kx + 50 = 0 యొక్క ఒక మూలము 5 అయిన k విలువ ఎంత ?
సాధన.
x2 + kx + 50 = 0 యొక్క ఒక మూలము 5.
∴ (5)2 + k(5) + 50 = 0
= 5k = – 75
⇒ k = [latex]\frac{-75}{5}[/latex] = – 15
ప్రశ్న 126.
ప్రవచనం-I: ax2 + bx + c = 0 యొక్క మూలాల మొత్తం [latex]\frac{-b}{a}[/latex] కు సమానము.
‘ప్రవచనం-II : ax2 + bx + c = 0 వర్గ సమీకరణం ఎల్లప్పుడు రెండు వాస్తవ మూలాలను కలిగి ఉంటుంది.
(A) I సత్యం , II అసత్యం .
(B) I సత్యం, II సత్యం
(C) I అసత్యం, II సత్యం
(D) I అసత్యం, II అసత్యం
జవాబు.
(A) I సత్యం , II అసత్యం .
![]()
ప్రశ్న 127.
మూలాలు సమానంగా గల వర్గసమీకరణానికి ఒక ఉదాహరణనివ్వండి.
సాధన.
మూలాలు సమానంగా గల వర్గసమీకరణానికి ఉదాహరణ
(x – 2) (x – 2) = 0 = x2 – 4x + 4 = 0
ప్రశ్న 128.
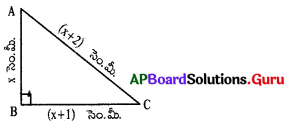
పై లంబకోణ త్రిభుజం ABCలో AB భుజం పొడవును సాధనగా గల వర్గ సమీకరణ ప్రామాణిక రూపంను రాయండి.
సాధన.
AC2 = AB + BC2
= (x + 2)2 = x2 + (x + 1)2
= x2 + 4x + 4 = x2 + x2 + 2x + 1 [∵ (a + b)2 = a2 + 2ab + b2]
∴ x2 – 2x – 3 = 0
ప్రశ్న 129.
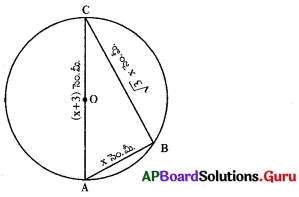
పై పటంలో ‘0’ వృత్త కేంద్రము మరియు AC = (x + 3) సెం.మీ. AB = x సెం.మీ. BC = √3 x సెం.మీ అయిన x విలువ కలిగిన వర్గ సమీకరణంను కనుగొనుము.
సాధన.
∠B = 90° (∵ B అర్ధవృత్తంలోని కోణము) 3
∴ AB2 + BC2 = AC2
⇒ x2 + (√3 x)2 = (x + 3)2
![]()
∴ 3x2 – 6x – 9 = 0
ప్రశ్న 130.
kx (x – 2) + 6 = 0 యొక్క ఒక సాధన 3 అయిన k = ……………
(A) 2
(B) – 2
(C) 1
(D) – 1
జవాబు.
(B) – 2
సాధన.
kx (x – 2) + 6 = 0 యొక్క సాధన 3.
∴ k(3) (3 – 2) + 6 = 0
3k + 6 = 0 = 3k =-6 -6
∴ k = [latex]\frac{-6}{3}[/latex] = – 2
ప్రశ్న 131.
α, β లు శూన్యాలుగా గల వర్గబహుపది k(x2 – (α + β)x + αβ) అయిన α, β లు మూలాలుగా గల వర్గ బహుపదిని తెల్పండి.
జవాబు.
x2 – (α + β)x + αβ = 0
ప్రశ్న 132.
క్రింది పటంలో గ్రాఫ్ సూచించే వర్గ సమీకరణం యొక్క మూలాలు ఏవి ?
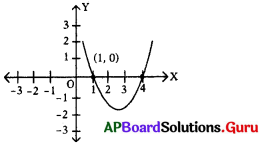
జవాబు.
మూలాలు 1, 4.
ప్రశ్న 133.
మొత్తము 27, లబ్ధము 182 అయ్యే విధంగా గల రెండు సంఖ్యలను కనుగొనుటకు అవసరమైన వర్గ సమీకరణం x2 – kx + 182 = 0 అయిన kను కనుగొనుము.
జవాబు.
k = 27 (∵ k విలువ మూలాల మొత్తానికి సమానము)
![]()
ప్రశ్న 134.
“ఒక సంఖ్య మరియు సంఖ్య యొక్క వ్యుత్రమాల మొత్తం [latex]\frac{10}{3}[/latex]” అయిన ఇచ్చిన నియమాలను తృప్తిపరిచే వర్గ సమీకరణం
(i) x + [latex]\frac{1}{x}[/latex] = [latex]\frac{10}{3}[/latex]
(ii) 3x2 = 10x + 3 = 0
(A) i మాత్రమే సత్యం
(B) ii మాత్రమే సత్యం
(C) i మరియు ii లు రెండూ సత్యం
(D) i మరియు ii’లు రెండూ అసత్యం
జవాబు.
(C) i మరియు ii లు రెండూ సత్యం
ప్రశ్న 135.
x2 – 5x + 6 = 0 మూలాలు α, β అయిన [latex]\frac{1}{\alpha}+\frac{1}{\beta}[/latex] విలువను కనుగొనుము.
సాధన.
x2 – 5x + 6 = 0 యొక్క మూలాలు α, β
∴ α + β = 5, αβ = 6
[latex]\frac{1}{\alpha}+\frac{1}{\beta}[/latex] = [latex]\frac{\beta+\alpha}{\alpha \beta}[/latex] = [latex]\frac{5}{6}[/latex]
(లేదా)
x2 – 5x + 6 = 0 యొక్క మూలాలను α, β
విలువలు కనుగొని [latex]\frac{1}{\alpha}+\frac{1}{\beta}[/latex] విలువ కనుగొనవచ్చును.
ప్రశ్న 136.
x – [latex]\frac{1}{3}[/latex] = 3 వర్గ సమీకరణంను ప్రామాణిక రూపులోకి మార్చండి.
సాధన.
x – [latex]\frac{1}{x}[/latex] = 3 ⇒ [latex]\frac{x^{2}-1}{x}[/latex] = 3 ⇒ x2 – 1 = 3x
⇒ x2 – 3x – 1 = 0
ప్రశ్న 137.
x – [latex]\frac{1}{x}[/latex] = 0 మరియు x ≠ 0 అయిన X ధన విలువ ఎంత ?
సాధన.
x = [latex]\frac{1}{x}[/latex] ⇒ x2 = 1 ⇒ x = √1 = ± 1
∴ x యొక్క ధన విలువ = 1
ప్రశ్న 138.
6x2 – x – 2 = 0 వర్గ సమీకరణ మూలాలు [latex]\frac{2}{3}[/latex] మరియు -[latex]\frac{1}{2}[/latex] అయిన p(x) = 6x2 – x – 2 వర్గబహుపది యొక్క శూన్యాలు ఏవి ?
సాధన.
p(x) = 6x2 – x – 2 యొక్క శూన్యాలు [latex]\frac{2}{3}, \frac{-1}{2}[/latex]
ప్రశ్న 139.
1, 2 శూన్యాలుగాగల వర్గబహుపది p(x) = x2 – 3x + 2 అయిన log1010, log10100 విలువలు మూలాలుగా గల -వర్గ సమీకరణాన్ని తెల్పండి.
సాధన.
log1010 = 1,
log10100 = log10102 = 2log1010 = 2
∴ 1, 2 శూన్యాలుగా గల వర్తబహుపది
= x2 – 3x + 2 = 0 (ఇవ్వబడినది).
ప్రశ్న 140.
x – [latex]\frac{3}{x}[/latex] = 2 వర్గ సమీకరణ మూలాలలో ఒకటి – 1 అయిన రెండవ మూలము ఏది ?
సాధన.
x – [latex]\frac{3}{x}[/latex] = 2 = x2 – 2x – 3 = 0 యొక్క ఒక
మూలం α = – 1.
α + β = 2 ⇒ – 1 + β = 2 ⇒ β = 3,
రెండవ మూలం = 3
![]()
ప్రశ్న 141.
క్రింది వానిలో ax2 + bx + c = 0కు సంబంధించి నది ఏది సత్యం ?
(A) b2 – 4ac > 0 అయిన మూలాలు విభిన్న వాస్తవ సంఖ్యలు.
(B) b2 – 4ac = 0 అయిన మూలాలు సమాన వాస్తవ సంఖ్యలు.
(C) b2 – 4ac < 0 అయిన వాస్తవ సంఖ్యలు కావు.
(D) పైవి అన్నీ
జవాబు.
(D) పైవి అన్నీ
ప్రశ్న 142.
x2 – 7x + 12 = 0 నకు మూలాల స్వభావం తెల్పండి.
సాధన.
x2 – 7x + 12 = 0 యొక్క విచక్షణి
b2 – 4ac = (- 7)2 – 4(1)(12)
= 49 – 48 = 1 > 0
∴ మూలాలు విభిన్న వాస్తవ సంఖ్యలు.
ప్రశ్న 143.
x2 – kx + 16 = 0 నందు మూలాలు అసమానాలు, వాస్తవాలు అయిన క్రింది వానిలో ఏది సత్యం ?
(A) k = 8.
(B) k > 8
(C) k < 8
(D) ఏదీకాదు
జవాబు.
(D) ఏదీకాదు
సాధన.
x2 – kx + 16 = 0 యొక్క మూలాలు అసమాన వాస్తవ సంఖ్యలు.
∴ b2 – 4ac > 0 ⇒ (- k)2 – 4(1)16 > 0
k2 – 64 > 0 ⇒ k2 > 64 ⇒ k > √64
∴ k > 8 (లేదా) k < – 8.
ప్రశ్న 144.
క్రింది పటంలోని వర్గ సమీకరణం యొక్క మూలాల గూర్చి నీవు ఏమి చెప్పగలవు ?
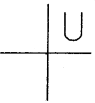
జవాబు.
మూలాలు వాస్తవ సంఖ్యలు కావు.
ప్రశ్న 145.
x2 – 36 = 0 యొక్క గ్రాఫ్ 20 అయిన a + b విలువ ఎంత ?
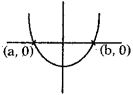
సాధన.
a, b లు ఇచ్చిన వర్గసమీకరణం మూలాలు.
∴ a + b = [latex]\frac{-b}{a}[/latex] = [latex]\frac{0}{1}[/latex] = 0
(లేదా)
x2 – 36 = 0 ⇒ x2 = 36 ⇒ x = √36 = ±6
గ్రాఫ్ ప్రకారం మూలాలు a, b
∴ a = – 6, b = 6
∴ a + b = (- 6) + 6 = 0
![]()
ప్రశ్న 146.
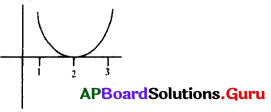
పై పటం సూచించే వర్గ సమీకరణం నందు మూలాల మొత్తంను తెల్పండి.
(A) 2
(B) 4
(C)8
(D)
సాధన.
(B) 4
మూలాలు సమానాలు మరియు 2, 2.
∴ మూలాల మొత్తం = 2 + 2 = 4
ప్రశ్న 147.

(A) 1
(B) 2
(C) 3
(D) 6
జవాబు.
C
సాధన.
మూలాలు 1,3
p మూలాల మొత్తం అవుతుంది.
∴ p = 1 + 3 = 4
q మూలాల లబ్ధం అవుతుంది.
∴ q = (1) (3) = 3
ప్రశ్న 148.
x2 – 4x + 3 = 0 యొక్క మూలాలు 1, 3 అయిన x2 – 4x + 3 = 0 యొక్క రేఖాచిత్రం (గ్రాఫ్) X- అక్షాన్ని ఖండించే బిందువులను తెల్పండి.
సాధన.
X – అక్షాన్ని ఖండించే బిందువులు (1, 0) మరియు (3, 0).
ప్రశ్న 149.
sin 90°, sec 60° విలువలు శూన్యాలుగా గల వర్గ సమీకరణాన్ని రాయండి.
సాధన.
sin 90° = 1, sec 60° = 2.
∴ 1, 2 శూన్యాలుగా గల వర్గ సమీకరణం
x2 – (1 + 2)x + (1) (2) = 0 .
x2 – 3x + 2 = 0
ప్రశ్న 150.
ax2 + bx + c = 0 యొక్క మూలాల మొత్తంను రాయండి.
సాధన.
[latex]\frac{-b}{a}[/latex]
![]()
ప్రశ్న 151.
ax2 + bx – c = 0 యొక్క మూలాల లబ్దంను – తెల్పండి.
జ.
[latex]\frac{c}{a}[/latex]
ప్రశ్న 152.
(x + 5) (x – 6) = 0 తో సూచింపబడే వర్గ సమీకరణం యొక్క మూలాల మొత్తం ఎంత ?
సాధన.
మూలాలు – 5, 6 .
∴ మూలాల మొత్తం = (- 5) + 6 = 1
ప్రశ్న 153.
2x2 – 1 = 0 వర్గ సమీకరణమునకు sin θ ఒక మూలము (0 ≤ 90°) అయిన ‘θ’ విలువను కనుగొనుము.
సాధన.
2x2 – 1 = 0కు sin θ ఒక మూలము.
∴ 2 sin2θ – 1 = 0
⇒ 2 sin2θ = 1 ⇒ sin2θ = [latex]\frac{1}{2}[/latex]
∴ sin θ = [latex]\sqrt{\frac{1}{2}}[/latex] = [latex]\frac{1}{\sqrt{2}}[/latex]
∴ θ = 45°
ప్రశ్న 154.
ఒక వర్గ సమీకరణం మూలాలు వాస్తవ సంఖ్యలు అయిన ఆ మూలాల సంఖ్య.
(A) 0
(B) కనీసం
(C) గరిష్ఠంగా 2
(D) B మరియు C
జవాబు.
(D) B మరియు C
ప్రశ్న 155.
x2 – 7x + 12 = 0 వర్గ సమీకరణం యొక్క మూలాల లబ్ధంను కనుగొనుము.
సాధన:
మూలాల లబ్ధం = [latex]\frac{c}{a}[/latex] = [latex]\frac{12}{1}[/latex] =12
ప్రశ్న 156.
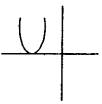
వర్గ సమీకరణ గ్రాఫ్ పటంలో చూపిన విధంగా X- అక్షాన్ని ఒకే బిందువు వద్ద తాకిన పై సందర్భంలో విచక్షణి గూర్చి నీవు ఏమి చెప్పగలవు?
జవాబు.
విచక్షణి = 0
ప్రశ్న 157.

ను సూచించు వర్గ బహుపది మూలాల స్వభావాన్ని రాయండి.
జవాబు.
మూలాలు సమాన వాస్తవ సంఖ్యలు.
గమనిక: ఇచ్చిన సమాచారం ఆధారంగా 158 – 160 వరకు గల ప్రశ్నలకు సమాధానాలు రాయండి. వర్గసమీకరణము x2 – 7x + 12 = 0.
ప్రశ్న 158.
ఇచ్చిన వర్గసమీకరణ విచక్షణిని కనుగొనుము.
సాధన.
విచక్షణి. b2 – 4ac = (-7)2 – 4(1) (12)
= 49 – 48 = 1
ప్రశ్న 159.
ఇచ్చిన వర్గసమీకరణ మూలాలను పొడవు, వెడల్పులుగా గల దీర్ఘచతురస్ర చుట్టుకొలత ఎంత ?
సాధన.
మూలాలు α, β అనుకొనుము.
l = α, b = β అనుకొనుము.
దీర్ఘచతురస్ర చుట్టుకొలత = 2(1 + b)
= 2(α + β)
= 2[latex]\left(\frac{-b}{a}\right)[/latex]
= 2[latex]\left(\frac{-(-7)}{1}\right)[/latex]
= 14 యూనిట్లు
![]()
ప్రశ్న 160.
ఇచ్చిన వర్గసమీకరణ మూలాలను పొడవు, వెడల్పులుగా గల దీర్ఘచతురస్ర వైశాల్యమును లెక్కించండి.
సాధన.
దీర్ఘచతురస్ర వైశాల్యం = lb = αβ
= [latex]\frac{c}{a}[/latex] = [latex]\frac{12}{1}[/latex] = 12 చ.యూ.
ప్రశ్న 161.
వెడల్పు కంటె పొడవు 5 ఎక్కువగా గల దీర్ఘచతురస్ర వైశాల్యం a2 చ.యూ. పై సమాచారాన్ని సూచించు వర్గ సమీకరణం ఏది ?
(A) x2 + 5x – 25 = 0
(B) x(x + 5) = a
(C) x2 + 6x – a = 0
(D) పైవేవీకావు
సాధన.
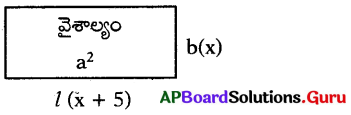
దీర్ఘచతురస్ర వైశాల్యం = lb = a2
∴ (x + 5)x = a2
∴ కావలసిన వర్గసమీకరణం x2 + 5x – a2 = 0.
ప్రశ్న 162.
2 sin2 θ – 3 sin e + 10 = 0 సమీకరణంలో sin θ = x అయిన ఏర్పడే x లో వర్గసమీకరణాన్ని రాయండి.
జవాబు.
2x2 – 3x + 10 = 0.
ప్రశ్న 163.
ax2 + bx + c = 0 వర్గసమీకరణం యొక్క మూలాలు సమానమయ్యే సందర్భంలో వర్గసమీకరణ గ్రాఫ్ X – అక్షాన్ని స్పర్శించే బిందువును తెల్పండి.
జవాబు.
[latex]\left(\frac{-b}{2 a}, 0\right)[/latex]
ప్రశ్న 164.
x2 – 3x + p= 0 యొక్క ఒక మూలం ‘0’ అయిన ‘p’ విలువ ఎంత ?
సాధన.
x2 – 3x + p = 0 యొక్క ఒక మూలం
(0)2 – 3(0) + p = 0 ⇒ p = 0
ప్రశ్న 165.
రెండు వరుస ధనపూర్ణ సంఖ్యల లబ్దం 306. ఈ ధన పూర్ణసంఖ్యలను కనుగొనుటకు అవసరమైన వర్గ సమీకరణాన్ని రాబట్టుము.
సాధన.
చిన్న ధన సంఖ్య = x అనుకొనుము.
పెద్ద ధన సంఖ్య = x + 1
x(x + 1) = 306 ⇒ x2 + x – 306 = 0
(లేదా)
పెద్ద ధన సంఖ్య = x అనుకొనుము
చిన్న ధన సంఖ్య = x – 1
x(x – 1) = 306 ⇒ x2 – x – 306 = 0
ప్రశ్న 166.
x + [latex]\frac{1}{x}[/latex] = వర్గ సమీకరణమున 1 ఒక మూలం అని చూపుము.
సాధన.
x + [latex]\frac{1}{x}[/latex] లో x = 1 ని ప్రతిక్షేపించగా
(1) + [latex]\frac{1}{(1)}[/latex] = 2
1 + 1 = 2
2 = 2
∴ L.H.S. = R.H.S.
∴ 1 ఒక మూలము.
![]()
ప్రశ్న 167.
క్రింది వానిలో సమాన మూలాలు – 1 గా గల వర్గ సమీకరణం ఏది ?
(A) x2 + 2x = – 1
(B) (x + 1)2 = 0
(C) x2 = – (2x + 1)
(D) పైవన్నీ
జవాబు.
(D) పైవన్నీ
ప్రశ్న 168.
ఈ క్రింది వానిలో వర్గ సమీకరణం కానిది ఏది ?
(A) x2 = 5
(B) (x + 1)2 = (2x – 3)2
(C) (2x + 5)2 = (2x – 1)2
(D) x3 + 3×22 + 1 = (x – 4)3
జవాబు.
(C) (2x + 5)2 = (2x – 1)2
ప్రశ్న 169.
జతపరుచుము. వర్గ సమీకరణం x2 – 10x + 9 = 0

(A) i-a, ii-c, iii-b, iv-d
(B) i-d, ii-b, iii-c, iv-a
(C) i-b, ii-a, iii-d, iv-c
(D) i-c, ii-b, iii-d, iv-a
జవాబు.
(B) i-d, ii-b, iii-c, iv-a
ప్రశ్న 170.
30 మీ. ఎత్తుగల కొబ్బరి చెట్టు నుండి ఒక కొబ్బరికాయ h = 30 + 7t – t2ను తృప్తిపరిచేటట్లు పడుతుంది. అయితే అది భూమిని చేరుటకు పట్టు కాలమును లెక్కించుటకు ఈ క్రింది వానిలో ఏది సరైన వర్గ సమీకరణము?
(A) 30 = 30 + 7t – t2
(B) – 30 = 30 + 7t + t2
(C) 0 = 30 + 7t – t2
(D) 0 = 7t – t2
జవాబు.
(C) 0 = 30 + 7t – t2
ప్రశ్న 171.
నిలకడ నీటిలో బోటు వేగం 18 mps, ప్రవాహ వేగం x mps అయిన ప్రవాహానికి ఎదురు దిశలో బోటు , వేగము ……….. mps.
జవాబు.
18 – x
ప్రశ్న 172.
క్రింది ఏ సందర్భంలో వర్గసమీకరణ భావనను ఉపయోగించుకొంటాము ?
(A) ప్రయోగించిన రాకెట్ యొక్క గమన మార్గాన్ని నిర్ణయించడంలో .
(B) పైకి విసిరిన వస్తువు యొక్క పదాన్ని నిర్ణయించడంలో
(C) వాహనం యొక్క బ్రేకును వేసినప్పుడు అది ప్రయాణించే మార్గాన్ని లెక్కించడం
(D) పై అన్ని సందర్భాలలో
జవాబు.
(D) పై అన్ని సందర్భాలలో
ప్రశ్న 173.
x2 – 8x + 16 = 0 యొక్క మూలాలను భుజాలుగా గల చతురస్రం యొక్క వైశాల్యము ఎంత ?
సాధన.
మూలాలు చతురస్ర భుజాలు α, β అనుకొనుము. (α = β).
చతురస్ర వైశాల్యం = మూలాల లబ్ధం .
= [latex]\frac{c}{a}[/latex] = 16
![]()
ప్రశ్న 174.
క్రింది వర్గసమీకరణాలను వాని మూలాలకు జత చేయడంలో సరైన సమాధానాన్ని ఎన్నుకొనుము.
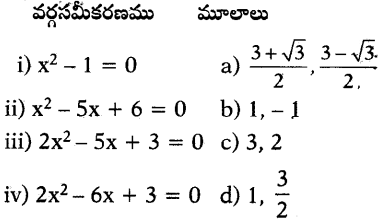
(A) i-b, ii-a, iii-c, iv-d
(B) i-c, ii-b, iii-a, iv-d
(C) i-b, ii-c, iii-d, iv-a
(D) i-b, ii-d, iii-a, iv-c
జవాబు.
(C) i-b, ii-c, iii-d, iv-a
ప్రశ్న 175.
x2 – 6x + 8 = 0 యొక్క మూలాల సగటు ఎంత ?
సాధన.
మూలాలు α, β అనుకొనుము.
α + β = [latex]\frac{-b}{a}[/latex] = [latex]\frac{-(-6)}{1}[/latex] = 6
α, β ల సగటు = [latex]\frac{\alpha+\beta}{2}=\frac{6}{2}[/latex] = 3
ప్రశ్న 176.
x2 – 2x – 8 = 0 యొక్క మూలాలు α, β మరియు α, k, β లు అంకశ్రేణిలో ఉంటే k విలువ ఎంత ?
సాధన.
x2 – 2x – 8 = 0 యొక్క మూలాలు α, β.
∴ α + β = [latex]\frac{-b}{a}[/latex] = [latex]\frac{-(-2)}{1}[/latex] = 2
α, k, β లు A.P లో ఉంటే k = [latex]\frac{\alpha+\beta}{2}=\frac{2}{2}[/latex] = 1
ప్రశ్న 177.
3 మరియు 4 మూలాలుగా కల్గిన వర్గసమీకరణాన్ని రాయండి.
జవాబు.
x2 – 7x + 12 = 0
![]()
ప్రశ్న 178.
వర్గసమీకరణం ax2 + bx + c = 0 యొక్క విచక్షణి b2 – 4ac< 0 అయ్యే సందర్భానికి చిత్తు రేఖాచిత్రం (గ్రాఫ్) గీయండి.
జవాబు.