AP 10th Class Maths Bits 3rd Lesson బహుపదులు

Practice the AP 10th Class Maths Bits with Answers 3rd Lesson బహుపదులు on a regular basis so that you can attempt exams with utmost confidence.

AP Board 10th Class Maths Bits 3rd Lesson బహుపదులు

ప్రశ్న 1.
రేఖీయ బహుపది ax + b యొక్క శూన్య విలువ ఎంత?
సాధన.
ax + b = 0 ⇒ ax = -b ⇒ x = \(\frac{-b}{a}\)
∴ ax + b యొక్క శూన్య విలువ \(\frac{-b}{a}\)

ప్రశ్న 2.
ax² + bx + c యొక్క శూన్యాల లబ్దం ‘0’ అయిన
(A) a = 0
(B) b = 0
(C) c = 0
(D) a = c.
జవాబు.
(C) c = 0

ప్రశ్న 3.
x³ – 5x² + 6x యొక్క రెండు శూన్యాలు 2, 3 అయిన మూడవ శూన్యము ఏది ?
సాధన.
x³ – 5x² + 6x యొక్క రెండు శూన్యాలు 2, 3.
α = 2, β = 3 అనుకొనుము. γ = \(\frac{-b}{-a}\)
∴ శూన్యాల మొత్తం α + β + γ = 2
2 + 3 + γ = \(\frac{-(-5)}{1}\) = 5
γ = 0
(లేదా)
x³ – 5x² + 6x లో స్థిరపదం లేదు కావున ‘O’ ఒక శూన్యం అవుతుంది.
∴ కావున మూడవ శూన్యం = ‘0’

ప్రశ్న 4.
5x⁷ – 6x⁵ + 7x – 6 బహుపది పరిమాణం ఎంత?
జవాబు.
7

ప్రశ్న 5.
2x² – 8x + 6 బహుపది శూన్యాల మొత్తంను కనుగొనుము.
సాధన.
శూన్యాల మొత్తం = \(\frac{-b}{a}\) = \(\frac{-(-8)}{2}\) = 4

ప్రశ్న 6.
3x³ – 5x² – 11x – 3 ఘన బహుపది శూన్యాల లబ్ధం ఎంత ?
సాధన.
ఘనబహుపది శూన్యాల లబ్ధం = \(\frac{-d}{a}\) = \(\frac{-(-3)}{2}\) = 1

ప్రశ్న 7.
p(x) = 4x² + 3x + 1 బహుపది x = – 1 వద్ద బహుపది విలువ ఎంత ?
సాధన.
p(- 1) = 4(- 1)² + 3(- 1) + 1
= 4 – 3 + 1 = 2

ప్రశ్న 8.
px + q రేఖీయ బహుపది యొక్క శూన్య విలువను రాయండి.
సాధన.
px + q = 0 ⇒ px = – q ⇒ x = \(\frac{-\mathrm{q}}{\mathrm{p}}\)
∴ px + q యొక్క శూన్య విలువ \(\frac{-\mathrm{q}}{\mathrm{p}}\)

ప్రశ్న 9.
4y² – 5y + 1 ఒక ……………….
(A) రేఖీయ బహుపది
(B) ఘన బహుపది
(C) స్థిర బహుపది
(D) వర్గ బహుపది
జవాబు.
(D) వర్గ బహుపది

ప్రశ్న 10.
4x + 6y = 18 యొక్క రేఖా చిత్రం ఒక ……………. అది మూల బిందువు గుండా వెళ్ళదు.
(A) వక్రరేఖ
(B) కర్ణము
(C) సరళరేఖ
(D) ఏదీకాదు
జవాబు.
(C) సరళరేఖ

ప్రశ్న 11.
x² – x – 6 బహుపది శూన్యాలు α, β అయిన α² + β² విలువ ఎంత?
సాధన.
α, β = \(\frac{c}{a}\) = \(\frac{-6}{1}\) = – 6
∴ α²β² = (αβ)² = (- 6)² = 36

ప్రశ్న 12.
p(x) = x² – 8x + kను (x – 1) తో భాగించగా శేషం ‘6’ అయిన ఓ విలువను కనుగొనుము.
సాధన.
p(x) = x² – 8x + kను (x – 1) చే భాగించగా
శేషం p(1) = 6
∴ p(1) = (1)² – 8(1) + k = 6
⇒ 7 + k = 6
⇒ k = 13
(లేదా)

లెక్క ప్రకారం, శేషం = 6
∴ k – 7 = 6 ⇒ k = 13

ప్రశ్న 13.
రేఖీయ బహుపది ax – b శూన్య విలువ ఏది ?
సాధన.
ax – b = 0 ⇒ ax = b ⇒ x = \(\frac{b}{a}\)
∴ ax – b యొక్క శూన్య విలువ = \(\frac{b}{a}\)

ప్రశ్న 14.
2x² – 3x + 6 యొక్క శూన్యాల లబ్ధంను కనుగొనుము.
సాధన.
శూన్యాల లబ్ధం = \(\frac{c}{a}\) = \(\frac{6}{2}\) = 3

ప్రశ్న 15.
bx² + ax + c యొక్క శూన్యాల మొత్తంను రాయండి.
సాధన.

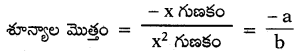
ప్రశ్న 16.
x³ + 3x² – x + 2 యొక్క శూన్యాలు α, β, γ అయిన αβγ విలువ ఎంత ?
సాధన.
αβγ = \(\frac{-\mathrm{d}}{\mathrm{a}}\) = \(\frac{-2}{1}\) = 2

ప్రశ్న 17.
2, 3 లను శూన్యాలుగా కలిగిన వర్గ బహుపదిని రాయండి.
సాధన.
2, 3 లను శూన్యాలుగా గల వర్గ బహుపది
k[x² – (α + β)x + αβ] = k[x² – (5)x + 6]
k = 1,
∴ కావలసిన వర్గబహుపది = x² – 5x + 6

ప్రశ్న 18.
ఈ క్రింది వాటిలో ఒకే ఒక శూన్య విలువ కలిగిన బహుపది ఏది ?
(A) p(x) = 2x² – 3x + 4
(B) p(x) = x² – 2x + 1
(C) p(x) = 2x + 3
(D) p(x) = 5
సాధన.
B, C [ఒకే శూన్యం ఉంటే b² – 4ac = 0 కావాలి]
Aలో p(x) = 2x² – 3x + 4,
= 9 – 4(2) (4) = 9 – 32 < 0
Bలో p(x) = x² – 2x + 1,
= 4 – 4(1) (1) = 0
∴ B సరైన సమాధానం.
(C)లో p(x) = 2x + 3.
⇒ 2x + 3 = 0 ⇒ x = \(\frac{-3}{2}\) (ఒకే శూన్య విలువ).

ప్రశ్న 19.
క్రింది పటంలో దీర్ఘ చతురస్రంను పరిశీలించిన, దాని వైశాల్యానికి బహుపది ప్రమేయంను కనుగొనుము.

సాధన.
వైశాల్య బహుపది A(x) = (10 – x) (x + 3)
= 10x + 30 – x² – 3x
= – x² + 7x + 30

ప్రశ్న 20.
7x¹⁷ – 17x¹¹ + 27x⁵ – అను బహుపదిలో x⁷ యొక్క గుణకం ఎంత ?
జవాబు.
0

ప్రశ్న 21.
x² + x + 1 యొక్క శూన్యాలు α, β అయిన \(\frac{1}{\alpha}+\frac{1}{\beta}\) విలువను లెక్కించండి.
సాధన.
x² + x + 1 యొక్క శూన్యాలు α, β.

ప్రశ్న 22.
x³ – 2x² + 3x – 4 బహుపది శూన్యాల మొత్తం ఎంత ?
సాధన.
శూన్యాల మొత్తం = \(\frac{-b}{a}\) = \(\frac{-(-2)}{1}\) = 2

ప్రశ్న 23.
p(x) = x² + kx – 8 యొక్క ఒక శూన్యము 4 అయిన k విలువ ఎంత ?
సాధన.
p(x) = x² + kx – 8 యొక్క ఒక శూన్యం α = 4
∴ p(4) = 0
⇒ (4)² + k(4) – 8 = 0
⇒ 16 + 4k – 8 = 0
⇒ 4k + 8 = 0
⇒ 4k = – 8
⇒ k = \(\frac{-8}{4}\) =-2.

ప్రశ్న 24.
√2x² – 3x + 1 అనే బహుపది పరిమాణం ఎంత ?
జవాబు.
2

ప్రశ్న 25.
f(x) = 5x² + 13x + k యొక్క ఒక శూన్యము రెండవ శూన్యానికి విలోమమైన k = 5 అని చూపుము.
సాధన.
f(x) = 5x² + 13x + k యొక్క శూన్యాలు α, \(\frac{1}{\alpha}\) అనుకొనుము. (ఒకదానికొకటి విలోమాలు).

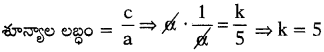
Short cut: ax² + bx + c వర్గ బహుపది శూన్యాలు ఒకదానికొకటి. గుణకార విలోమాలు (వ్యుత్ర్కమాలైన) అయిన a = c.
∴ k = 5

ప్రశ్న 26.
p(x) = x² + kx – 9 యొక్క ఒక శూన్యము ‘3’ అయిన kవిలువ ఎంత ?
సాధన.
p(x) = x² + kx – 9 యొక్క ఒక శూన్యం 3
కావున, p(3) = 0.
∴ p(3) = (3)² + k(3) – 9 = 0
⇒ 9 + 3k – 9 = 0 ⇒ 3k = 0
∴ k = 0

ప్రశ్న 27.
α, β, γలు ఘనబహుపది ax³ + bx² + cx + d, (a ≠ 0) యొక్క శూన్యాలు అయిన αβγ =
జవాబు.
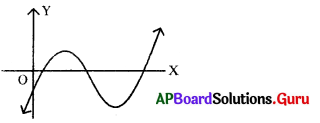
αβγ = \(\frac{-\mathrm{d}}{\mathrm{a}}\)

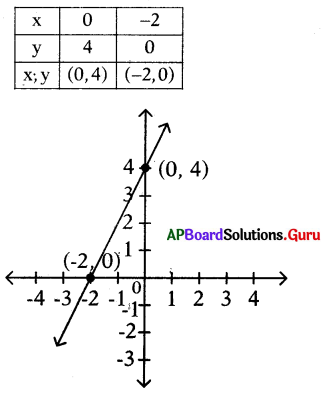
ప్రశ్న 28.
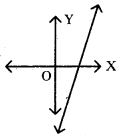
√2 మరియు – √2 శూన్యాలుగా గల వర్గ బహుపదిని కనుగొనుము.
సాధన.
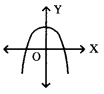
√2 మరియు – √Z శూన్యాలుగా గల వర్గ బహుపది
= x² – (α + β)x + αβ

= x² – 2

ప్రశ్న 29.
5x⁷ – 6x⁵ + 7x – 4 అనే బహుపది యొక్క పరిమాణం ఎంత ?
జవాబు.
7

ప్రశ్న 30.
ఈ క్రింది పటంలోని రేఖాచిత్రము సూచించు శూన్య విలువల సంఖ్య ఎంత ?

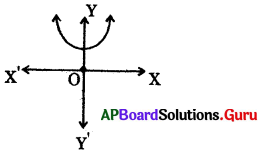
జవాబు.
0

ప్రశ్న 31.
x² + 5x + 6 బహుపది యొక్క శూన్యాల మొత్తము ఎంత ?
సాధన.
బహుపది శూన్యాల మొత్తం = \(\frac{-b}{a}\) = \(\frac{-5}{1}\) = 5

ప్రశ్న 32.
జతపరుచుము:
ax³ + bx² + cx + d, (a ≠ 0) అనే ఘన బహుపది యొక్క శూన్యాలు α, β, γ అయితే

(A) (i) – c, (ii) — b, (iii) – a
(B) (i) – a, (ii) – b, (iii) – C
(C) (i) – b, (ii) – a, (iii) – c
(D) (i) – c, (ii) – a, (iii) – b
జవాబు.
(A) (i) – c, (ii) — b, (iii) – a

ప్రశ్న 33.
5x – 3 అనునది ………… బహుపది.
(A) రేఖీయ
(B) వర్గ
(C) ఘన
(D) A మరియు B
జవాబు.
(A) రేఖీయ

ప్రశ్న 34.
రేఖాచిత్రములోని బహుపది యొక్క శూన్యాల సంఖ్య ……………………….

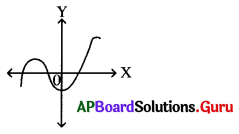
జవాబు.
3

ప్రశ్న 35.
α, βలు x² + 5x + k బహుపది యొక్క శూన్యాలు మరియు α – β = 3 అయిన kవిలువ ఎంత ?
(A) 6
(B) 9
(C) 5
(D) 4
సాధన.
x² + 5x + k యొక్క శూన్యాలు α, β మరియు α – β = 3
∴ α + β = \(\frac{-b}{a}\) = \(\frac{-5}{1}\)= – 5

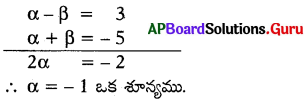
(- 1)² + 5(- 1) + k = 0
1 – 5 + k = 0 ⇒ k = 4
(లేదా)
α + β = – 5, αβ = k మరియు α – β = 3
(α + β)² = (α – β)² + 4αβ
(- 5)² = 3² + 4k
25 – 9 = 4k
⇒ k = \(\frac{16}{4}\) = 4

ప్రశ్న 36.
క్రింది వానిలో బహుపది కానిది ఏది
(A) x² + √2x + 4
(B) x² + 2√x + 4
(C) x² + 2x – √2
(D) √2 x² + 2x + 4
జవాబు.
(B) x² + 2√x + 4

ప్రశ్న 37.
క్రింది వానిలో బహుపది ఏది ?
(A) 2x³ + 4x² + 5
(B) \(\frac{2}{x^{3}}\) + 4x² + 4x + 9
(C) 2x³ + 4x² + 5√x + 9
D) 2x^{– 3} + 4x² + 5
జవాబు.
A

ప్రశ్న 38.
5x² – 4x³ + x – 1 యొక్క పరిమాణమును తెల్పండి.
జవాబు.
3

ప్రశ్న 39.
వర్గ బహుపది యొక్క పరిమాణము ఎంత?
జవాబు.
2

ప్రశ్న 40.
ఘన బహుపది యొక్క పరిమాణము ఎంత ?
జవాబు.
3

ప్రశ్న 41.
p(x) = x² – 5x – 6 అయిన p(- 2) విలువను కనుగొనుము.
సాధన.
p(- 2) = (- 2)² – 5(- 2) – 6
= 4 + 10 – 6 = 8

ప్రశ్న 42.
p(m) = m² – 3m + 1 అయిన p(1) + p(- 1) విలువను కనుగొనుము.
సాధన.
p(m) = m² – 3m + 1
∴ p(1) + p(- 1) = [(1)² – 3(1) + 1] + [(- 1)² – 3(- 1) + 1]
= (- 1) + (5) = 4

ప్రశ్న 43.
p(x) = 3x⁴ – 5x³ + 7x² – 9x + 2 అయిన p(x) కు చెందిన క్రింది వానిని జతపరుచుము.

(A) i-b, ii – c, iii-d, iv – a
(B) i – c, ii – a, iii – d, iv – b
(C) i – c, ii – b, iii – a, iv-d
(D) i – b, ii-d, iii – a, iv-c
జవాబు.
(B) i – c, ii – a, iii – d, iv – b

ప్రశ్న 44.
p(x) = x² – 9 యొక్క శూన్యాలను కనుగొనుము.
సాధన.
p(x) = x² – 9 = x² – 9 = 0.
⇒ x² = 9 ⇒ x = √9 = ± 3.
శూన్యాలు = 3, -3

ప్రశ్న 45.
p(x) = x² – 2x – 3 నకు 3 ఒక శూన్యం అవుతుందని నిరూపించుము.
సాధన.
p(x) = x² – 2x – 3
= (3)² – 2(3) – 3 = 9 – 9 = 0
p(3) = 0
కావున p(x)కు 3 ఒక శూన్యం అవుతుంది.

ప్రశ్న 46.
క్రింది పటంలో \(\overleftrightarrow{A B}\) ను సూచించే రేఖీయ బహుపది – యొక్క శూన్య విలువను తెల్పండి.

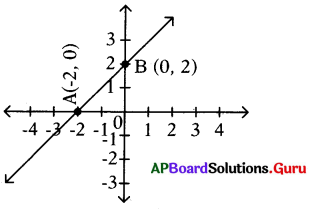
జవాబు.
– 2

ప్రశ్న 47.
p(x) = x² – 10x + 25 యొక్క శూన్య విలువను కనుగొనుము.
సాధన.
x² – 10x + 25 = x² – 2 ∙ x ∙ 5 + 5²
= (x – 5)²
⇒ (x – 5)² = 0
∴ x = 5
శూన్య విలువ = 5

ప్రశ్న 48.
బహుపది x³ – x² యొక్క ఒక శూన్యం ‘0’ అవుతుందని చూపుము.
సాధన.
p(x) = x³ – x²
p(0) = (0)³ – (0)² = 0
p(0) = 0 కావున ‘0’ ఒక శూన్యము.
(లేదా)
x³ – x² = 0 ⇒ x² (x – 1) = 0
x² = 0 (లేదా) x – 1 = 0
x = 0 (లేదా) x = 1
x³ – x² యొక్క శూన్యాలు 0, 1.
కావున ‘0’ ఒక శూన్యము.
(లేదా)
x³ – x² బహుపదిలో స్థిరపదం లేదు. కావున ‘0’ ఒక శూన్యం అవుతుంది.

ప్రశ్న 49.
బహుపది x³ – 4x యొక్క శూన్యాల సమితి ఏది ?
(A) {0, 2, -2}
(B) {0, 4, – 4}
(C) {0, 12, 12 }
(D) {1, -1, 2)
సాధన.
(A) {0, 2, -2}

వివరణ
x³ – 4x = 0 = x(x³ – 4) = 0
x = 0 (లేదా) x² – 4 = 0.
⇒ x² = 4 ⇒ x = √4 = ± 2
∴ శూన్యాలు 0, 2, – 2.

ప్రశ్న 50.
2 మరియు – 3 శూన్యాలుగా గల వర్గ బహుపదిని రాయండి.
సాధన.
α = 2, β = – 3
α + β = -1, αβ = – 6
వర్గబహుపది. = x² – (α + β)x + αβ
= x² – (- 1)x + (- 6)
= x² + x – 6

ప్రశ్న 51.
శూన్యాల మొత్తం (α + β) = 3, లబ్ధం (αβ) = – 10 గా గల వర్గ బహుపదిని రాయండి.
సాధన.
x² – (α + β)x + αβ = x² – 35 – 10.

ప్రశ్న 52.
x² + \(\frac{1}{6}\)x – 2 బహుపది యొక్క శూన్యాల మొత్తంను కనుగొనుము.
సాధన.
శూన్యాల మొత్తం = \(\frac{-b}{a}\) = \(\frac{-\frac{1}{6}}{1}\) = – \(\frac{1}{6}\)

ప్రశ్న 53.
\(\frac{1}{4}\) మరియు – 1 శూన్యాలుగా గల వర్గ బహుపదిని కనుగొనుము.
సాధన.
α = \(\frac{1}{4}\), β = – 1
∴ α + β = \(\frac{1}{4}\) + (- 1) = \(\frac{-3}{4}\)
αβ = (\(\frac{1}{4}\)) (- 1) = \(\frac{- 1}{4}\)
కావలసిన వర్గబహుపది
= k[x² – (α + β)x + αβ]
p(x) = k(x² – \(\left(\frac{-3}{4}\right)\)x – \(\frac{1}{4}\))
k = 4 అయిన p(x) = 4x² + 3x – 1.

ప్రశ్న 54.
y = ax² + bx + c రేఖాచిత్రం సూచించే పరావలయం పైవైపుకు వివృతం (తెరచుకొని)గా ఉంటే
(A) a < 0 (B) a = 0 (C) a > 0
(D) a = – 1
జవాబు.
(A) a < 0

ప్రశ్న 55.
ax² + bx + c యొక్క శూన్యాల మొత్తం ‘0’ అయిన
(A) a = 0
(B) b = 0
(C) c = 0
(D) a = c
జవాబు.
(B) b = 0

ప్రశ్న 56.
x² – 4x + 3 యొక్క శూన్యాల మొత్తం క్రింది వానిలో దేనికి సమానం?
(A) log₂16
(B) log₂8
(C) log₂4
(D) log₂2
జవాబు.
(A) log₂16

ప్రశ్న 57.
x² – 4 బహుపది యొక్క శూన్యాల మొత్తం ఎంత ?
సాధన.
శూన్యాల మొత్తం = \(\frac{-b}{a}\) = \(\frac{0}{1}\) = 0.

ప్రశ్న 58.
α, β లు x² – x – 6 యొక్క శూన్యా α + β విలువను రాయండి.
సాధన.
α + β = \(\frac{-b}{a}\) = \(\frac{-(-1)}{1}\) = 1

ప్రశ్న 59.
α, β లు x² + 2x – 8 యొక్క శూన్యా లైతే α²β + αβ² విలువను కనుగొనుము.
సాధన.
p(x) = x² + 2x – 8
∴ α + β = \(\frac{-b}{a}\) = \(\frac{-2}{1}\) = – 2
αβ = \(\frac{c}{a}\) = – 8
∴ α²β + αβ² = αβ(α + β)
= (-8) (-2) = 16

ప్రశ్న 60.
α, β లు x² – 3x + 2 యొక్క శూన్యాలైతే α³ + β³ విలువను లెక్కించండి.
సాధన.
α + β = 3, αβ = 2
α³ + β³ = (α + β)³ – 3αβ (α + β)
= (3)³ – 3(2) (3)
= 27 – 18 = 9
(లేదా)
p(x) = x² – 3x + 2 = 0
= x² – 2x – x + 2 = 0
= x(x – 2) – 1 (x – 2) = 0
= (x – 2) (x – 1) = 0
∴ x = 2 (లేదా) x = 1
α = 2, β = 1 అనుకొనుము.
α³ + β³ = (2)³ + (1)³ = 8 + 1 = 9

ప్రశ్న 61.
α, β లు 3x² + 125 – 12 కు శూన్యా లైతే క్రింది వానిలో ఏది సత్యం?
(A) α + β < αβ (B) α + β = αβ (C) α + β > αβ
(D) α + β = – αβ
సాధన.
(B) α + β = αβ

వివరణ
α + β = \(\frac{-12}{3}\) = – 4, αβ = \(\frac{-12}{3}\) = – 4
∴ α + β = αβ.

ప్రశ్న 62.
kx² – (k + 1) x – 3 బహుపది శూన్యాల మొత్తం \(\frac{7}{6}\) అయిన ఓ విలువ ఎంత ?
సాధన.
kx² – (k + 1) x – 3
శూన్యాల మొత్తం = \(\frac{7}{6}\)
\(\frac{-b}{a}\) = \(\frac{-[-(k+1)]}{k}\) = \(\frac{7}{6}\) ⇒ \(\frac{\mathrm{k}+1}{\mathrm{k}}\) = \(\frac{7}{6}\)
⇒ 7k = 6k + 6 ⇒ k = 6

ప్రశ్న 63.
x² + (a + 1) x + b యొక్క శూన్యాలు 3 మరియు 4 అయిన a, b విలువలు కనుగొనుము.
సాధన.
α = 3, β = 4 అనుకొనుము.
α + β = – (a + 1)
7 = – a – 1 ⇒ a = – 1 – 7 = – 8
αβ = \(\frac{\mathrm{b}}{1}\) ⇒ 12 = b
∴ a = – 8, b = 12.

ప్రశ్న 64.
x² – 2kx + 8 యొక్క ఒక శూన్యము 2 అయిన k విలువ ఎంత ?
సాధన.
p(x) = x² – 2kx + 8 యొక్క ఒక శూన్యము 2
అయిన p(2) = 0
∴ p(2) = (2)² – 2k(2) + 8
⇒ 4 – 4k + 8 = 0
⇒ 12 = 4k
∴ k = 3

ప్రశ్న 65.
0 మరియు √5 లు శూన్యాలుగా గల వర్గ బహుపదిని రాయండి.
సాధన.
x² – (α + β)x + αβ
= x² – (0 + √5)x + 0(√5)
∴ 0, √5 లు శూన్యాలుగా గల వర్గ బహుపది
= x² – √5 x

ప్రశ్న 66.
6x² – 5x + 1 యొక్క శూన్యాలు α, β అయితే \(\frac{1}{\alpha}+\frac{1}{\beta}\) విలువను గణించండి.
సాధన.

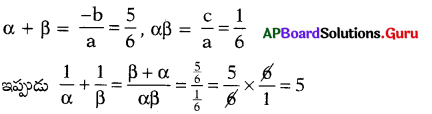
ప్రశ్న 67.
2x³ + kx² – 14x + 8 బహుపది యొక్క శూన్యాల మొత్తం \(\frac{5}{2}\) అయిన ఓ విలువ ఎంత ?
సాధన.
p(x) = 2x³ + kx² – 14x + 8 యొక్క శూన్యాల
మైతం \(\frac{5}{2}\)
\(\frac{-b}{a}=\frac{-k}{2}=\frac{5}{2}\) ⇒ k = – 5

ప్రశ్న 68.
x³ + 4x² + 5x – 2 యొక్క శూన్యాలు α, β, γ అయిన αβ + βγ + γα విలువ ఎంత ?
సాధన.
αβ + βγ + γα = \(\frac{c}{a}=\frac{5}{1}\) = 5

ప్రశ్న 69.
4x³ + 8x² – 6x – 2 యొక్క శూన్య విలువలు α, β, γ అయిన α + β + γ విలువ ఎంత?
సాధన.
α + β + γ = \(\frac{-b}{a}\) = \(\frac{-8}{4}\) = – 2

ప్రశ్న 70.
x³ + 5x² + kx + 4 యొక్క శూన్య విలువలు α, β, γ మరియు αβ + βγ + γα = 0 అయిన k విలువ ఎంత ?
సాధన.
αβ + βγ + γα = 0
\(\frac{\mathrm{C}}{\mathrm{a}}\) = \(\frac{\mathbf{k}}{1}\) = 0 ⇒ k = 0

ప్రశ్న 71.
x³ + 3x² – x – 2 యొక్క శూన్యాలు α, β, γ అయితే \(\frac{1}{\alpha^{3} \beta^{3} \gamma^{3}}\) విలువ ఎంత ?
సాధన.

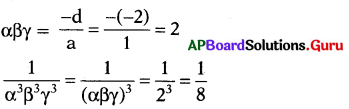
ప్రశ్న 72.
ఘన బహుభుజి ax³ + bx² + cx + d యొక్క రెండు శూన్యాలు ‘0’ అయిన మూడవ శూన్య విలువను కనుగొనుము.
సాధన.
ax³ + bx² + cx + d బహుపది యొక్క రెండు శూన్యాలు ‘0’
α = β = 0 అనుకొనుము.
శూన్యాల మొత్తం = α + β + γ = \(\frac{-b}{a}\)
0 + 0 + γ = \(\frac{-b}{a}\)
γ = \(\frac{-b}{a}\)
∴ మూడవ శూన్యము = \(\frac{-b}{a}\)

ప్రశ్న 73.
భాగహార నియమానికి సంబంధించి క్రింది వానిలో ఏది సత్యం ?
(A) అన్ని సందర్భాలలోను r(x) = 0
(B) r(x) పరిమాణం > g(x) పరిమాణం
(C) r(x) = 0 లేదా r(x) పరిమాణం < g(x) పరిమాణం
(D) r(x) = g(x)
జవాబు.
(D) r(x) = g(x)

ప్రశ్న 74.
x² – 5x + 6 నుx – 2 చే భాగించగా వచ్చు శేషము ఎంత ?
సాధన.
p(x) = x² – 5x + 6 ని (x – 2) చే భాగించగా
వచ్చు శేషము = p(2)
p(2) = 2² – 5(2) + 6 = 4 – 10 + 6 = 0
(లేదా)

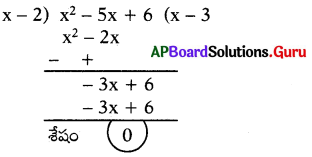
ప్రశ్న 75.
p(x) = x² – 5x + 6, q(x) = x – 2 మరియు r(x) = 0 అయిన g(x) ను కనుగొనుము.
సాధన.
p(x) = x² – 5x + 6, g(x) = x – 2 మరియు
r(x) = 0, g(x) = ?
భాగహార నియమం: p(x) = g(x) q(x) + r(x) x2 – 5x + 6 = g(x) (x – 2) + 0
∴ \(\frac{x^{2}-5 x+6}{x-2}\) = g(x) = x – 3.
(లేదా)

ప్రశ్న 76.
ప్రవచనం X: వర్గ బహుపది గరిష్ఠంగా 2 శూన్యాలను కలిగి ఉంటుంది.
ప్రవచనం Y: వర్గ బహుపది గరిష్ఠంగా 4 పదాలను కలిగి ఉంటుంది.
(A) X మాత్రమే సత్యం
(B) Y మాత్రమే సత్యం
(C) X, Y లు రెండూ సత్యం
(D)X, Y లు రెండూ అసత్యం
జవాబు.
(A) X మాత్రమే సత్యం

→ గమనిక: ఇవ్వబడిన వర్గ బహుపది p(x) యొక్క ను పరిశీలించి 77-79 వరకు గల ప్రశ్నలకు సమాధానాలు రాయండి.

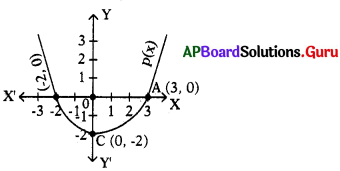
ప్రశ్న 77.
p(x) యొక్క శూన్యాలను తెల్పండి.
జవాబు.
p(x) శూన్యాలు = – 2, 3,

ప్రశ్న 78.
p(x) బహుపదిని కనుగొనుము.
సాధన.
α = -2, β = 3
p(x) = x² – (-2 + 3)x + (- 2) (3)
= x² – x – 6

ప్రశ్న 79.
p(x) గ్రాఫ్ యొక్క ఆకారం పేరును తెల్పండి.
జవాబు.
పరావలయము.

ప్రశ్న 80.
p(x) = 2x – 5 యొక్క శూన్య విలువను కనుగొనుము.
సాధన.
p(x) = 2x – 5 = 0 ⇒ 2x = 5 ⇒ x = \(\frac{5}{2}\)
p(x) యొక్క శూన్యము = \(\frac{5}{2}\)

ప్రశ్న 81.
p(x) = x² – 3x – 4 వక్రము x – అక్షాన్ని ఖండించే బిందువులలో ఒకటి (- 1, 0) అయిన మరొక బిందువును రాయండి.
సాధన.
p(x) = x² – 3x – 4 వక్రము X-అక్షాన్ని (- 1, 0) వద్ద ఖండిస్తున్నది.
కావున ఒక శూన్యం α = – 1
శూన్యాల మొత్తం α + β = \(\frac{-b}{a}\)
(-1) + β = \(\frac{-(-3)}{1}\)
⇒ β = 3 + 1 = 4
రెండవ శూన్యము = 4. కావున x – అక్షాన్ని ఖండించే ‘మరొక బిందువు (4, 0).
(లేదా)
αβ= – 4 = (- 1)β = – 4
∴ β = 4
(లేదా) .
p(x) = x² – 3x – 4 = 0
⇒ x² – 4x + x – 4 = 0
⇒ x(x – 4) + 1 (x – 4) = 0
⇒ (x – 4) (x + 1) = 0.
∴ శూన్యాలు 4, – 1
∴ X-అక్షాన్ని వక్రం ఖండించే బిందువులు (-1, 0), (4, 0).

ప్రశ్న 82.
x² – 2x – 15 యొక్క ఒక శూన్యము – 3 అయిన మరొక శూన్యమును కనుగొనుము.
సాధన.
x² – 21 – 15 యొక్క ఒక శూన్యము α = – 3.
α + β = \(\frac{-b}{a}\) = \(\frac{-(-2)}{1}\)
(- 3) + β = 2 ⇒ β = 5
αβ = \(\frac{c}{a}\) = – 15 ⇒ (- 3)β = – 15
∴ β = 5
రెండవ శూన్యము = 5.
(లేదా )
x² – 5x + 3x – 15 = 0
⇒ (x – 5) (x + 3) = 0
∴ శూన్యాలు 5, – 3.
రెండవ శూన్యము = 5.

ప్రశ్న 83.
క్రింది వానిలో, ఏది log₃27 మరియు log₃3 శూన్యాలుగా గల వర్గ బహుపది అవుతుంది?
(A) x² + 4x + 3
(B) x² – 4x + 3
(C) x² – 3x + 4
(D) x² + 3x – 4
సాధన.
(B) x² – 4x + 3

వివరణ
α = log₃ 27 = log₃3³ ⇒ 3 log₃ 3 = 3
β = log₃ 3 = 1
3, 1 శూన్యాలుగా గల వర్గబహుపది
= x² – 4x + 3.

ప్రశ్న 84.
p(x) బహుపది యొక్క పరిమాణం n అయిన p(x) లోని పదాల సంఖ్య గరిష్ఠంగా …………
(A) n – 1
(B) n
(C) n + 1
(D) 2n
జవాబు.
(C) n + 1

ప్రశ్న 85.
x² + 6x + k వక్రము X – అక్షాన్ని ఒకే ఒక బిందువు వద్ద స్పర్శిస్తుంటే ఓ విలువ ఎంత ?
సాధన.
x² + 6x + k వక్రము X – అక్షాన్ని ఒకే ఒక బిందువు
వద్ద స్పర్శిస్తుంటే శూన్యాలు సమానము.
∴ α = β
సమాన శూన్యాలు, α, α
శూన్యాల మొత్తం α + α = \(\frac{-b}{a}\)
2α = – 6 ⇒ α = – 3
శూన్యాల లబ్దం α∙α = k
⇒ (-3)∙(- 3) = k ⇒ k = 9
(లేదా)
శూన్యాలు సమానం అయిన
b² – 4ac = 0
6² – 4(1) (k) = 0
36 – 4k = 0
36 = 4k
∴ k = 9

ప్రశ్న 86.
క్రింది రేఖాచిత్రం సూచించు బహుపది యొక్క శూన్యాల సంఖ్య ఎంత?

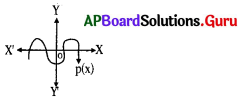
జవాబు.
4

ప్రశ్న 87.
క్రింది రేఖాచిత్రాన్ని సూచించే p(x) బహుపది యొక్క శూన్య విలువను రాయండి.

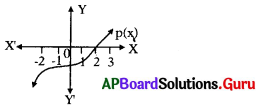
జవాబు.
1

ప్రశ్న 88.
x² + 7x + 10 బహుపది యొక్క శూన్యాల మొత్తం ఎంత ?
జవాబు.
– 7

ప్రశ్న 89.
√3 మరియు – √3 శూన్యాలుగా గల వర్గ బహుపదిని కనుగొనుము.
సాధన.
α = √5 , β = – √3
α + β = 0, αβ = – 3
వర్గబహుపది = x² – (α + β)x + αβ
= x² – 0x + (-3)
= x² – 3

ప్రశ్న 90.
4x² – 4x + k ఒకే ఒక శూన్యాన్ని కలిగి ఉంటే k విలువ log లో తెలుపగా
(A) log₁₀100
(B) log₁₀1
(C) log₁₀10
(D) log₁₀\(\frac{1}{10}\).
సాధన.
(C) log₁₀10

వివరణ
4x² – 4x + k ఒకే ఒక శూన్యాన్ని కలిగి ఉంటే
b² ⇒ 4ac = 16 = 16 k
⇒ k = 1 = log₁₀10

ప్రశ్న 91.
ఘన బహుపది యొక్క వక్రము X-అక్షాన్ని ఖండించే గరిష్ఠ బిందువుల సంఖ్య ఎంత ?
జవాబు.
3

ప్రశ్న 92.
స్థిరపదం లోపించిన ఘనబహుపది శూన్యాల లబ్దం ఎంత ?
జవాబు.
0

ప్రశ్న 93.
BC = 2x, AD = x + 4 గా గల త్రిభుజ వైశాల్యానికి వర్గ బహుపది A(x) ని కనుగొనుము.

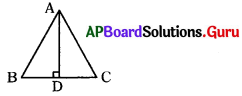
సాధన.
∆ABC వైశాల్యం A(x) = \(\frac{1}{2}\) BC × AD

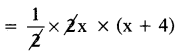
A(x) = x² + 4x

ప్రశ్న 94.
2x³ – 3kx² + 4x + 8 యొక్క శూన్యాల మొత్తం 6 అయితే k విలువ ఎంత?
సాధన.
α + β + γ = 6
\(\frac{-b}{a}\) = \(\frac{-(-3 k)}{2}\) = 6
⇒ 3k = 12
∴ k = 4

ప్రశ్న 95.
x³ + 3x² – x – 2 యొక్క శూన్యాలు α, β, γ అయిన αβγ విలువను రాయండి.
సాధన.
αβγ = \(\frac{-\mathrm{d}}{\mathrm{a}}=\frac{-(-2)}{1}\) = 2

ప్రశ్న 96.
x³ + 4x² – 5x – 2 యొక్క శూన్యాలు α, β, γ అయిన αβ + βγ + γα విలువ ఎంత?
సాధన.
αβ + βγ + γα = \(\frac{c}{a}\) = \(\frac{-5}{1}\) = – 5

ప్రశ్న 97.
p(x) = (x – 1) (x – 2) (x – 3) బహుపది యొక్క శూన్యాలు α, β, γ అయిన α³ + β³ + γ³ విలువ ఎంత?
సాధన.
p(x) = (x – 1) (x – 2) (x – 3)
శూన్యాలు, α = 1, β = 2, γ= 3
α³ + β³ + γ³ = (1)³ + (1)³ + (1)³
= 1 + 8 + 27 = 36

ప్రశ్న 98.
(x – 1) (x² – x – 6) యొక్క రెండు శూన్యాలు 3, – 2 అయిన మూడవ శూన్యము విలువ ఎంత?
సాధన.
(x – 1) (x² – x – 6) యొక్క రెండు శూన్యాలు
3, – 2.
∴ x – 1 ఒక కారణాంకము కావున,
3వ శూన్యము = 1

ప్రశ్న 99.
α, β లు శూన్యాలుగా గల వర్గ బహుపదిని రాయండి.
సాధన.
k (x² – (α + β)x + αβ) (లేదా)
x² – (α + β)x + αβ

ప్రశ్న 100.
వర్గ బహుపదిలో x పదము లేకుంటే ఆ వర్గ బహుపది శూన్యాల మొత్తము ఎంత?
జవాబు.
0

ప్రశ్న 101.
p(x) = g(x) . q(x) + r(x) లో g(x) రేఖీయ బహుపది మరియు q(x) ఘన బహుపది అయిన p(x) పరిమాణము ఎంత ?
సాధన.
p(x) పరిమాణం = g(x) పరిమాణం + q(x) పరిమాణం
= 1 + 3 = 4

ప్రశ్న 102.
p(x) = g(x) . q(x) + r(x) లో p(x) పరిమాణం 5 మరియు q(x) పరిమాణం 3 అయిన g(x) పరిమాణము ఎంత?
సాధన.
g(x) పరిమాణం = 5 – 3 = 2

ప్రశ్న 103.
p(x) = g(x) . q(x) + r(x) లో g(x), p(x) కు కారణాంకం అయితే r(x) గురించి నీవు ఏమి చెప్పగలవు ?
జవాబు.
r(x) = 0.

ప్రశ్న 104.
p(x) = x³ – 9x + k ను x – 1 తో భాగించగా శేషం 10 అయిన kవిలువ ఎంత?
సాధన.
p(1) = 0 ⇒ (1)³ – 9(1) + k = 0 ⇒ k = 8
(లేదా)

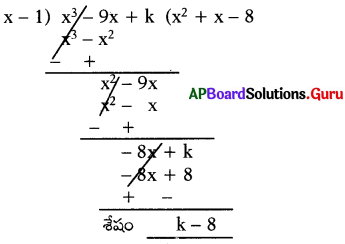
లెక్క ప్రకారం, శేషం = 0.
k-8 = 0
∴ k = 8

ప్రశ్న 105.
ax² + bx + c వర్గ బహుపది యొక్క గ్రాఫ్ X-అక్షాన్ని ఒకే ఒక బిందువు వద్ద స్పర్శిస్తుంటే ఆ స్పర్శ బిందువును తెల్పండి.
సాధన.
\(\left(\frac{-b}{2 a}, 0\right)\), [గ్రాఫ్ X – అక్షాన్ని ఒకే బిందువు వద్ద స్పర్శిస్తుంటే శూన్యాలు సమానాలు మరియు శూన్యాలు, \(\frac{-b}{2 a}, \frac{-b}{2 a}\), అవుతాయి.]

ప్రశ్న 106.
ఇచ్చిన దీర్ఘచతురస్రము యొక్క వైశాల్య బహుపది A(x) ను కనుగొనుము.

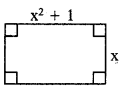
సాధన.
A(x) = పొడవు × వెడల్పు
= (x² + 1) (x) = x³ + x

ప్రశ్న 107.
α, β లు x² – 5x + k యొక్క శూన్యాలు మరియు α – β= 1 అయిన ఓ విలువ ఎంత ?
సాధన.
p(x) = x² – 5x + k యొక్క శూన్యాలు α, β
∴ α + β = \(\frac{-b}{a}\) = 5, αβ = \(\frac{c}{a}\) = k మరియు
α – β = 1, k = ?

3 + β = 5 ⇒ β = 2
∴ k = αβ = (3) (2) = 6

ప్రశ్న 108.
ఘన బహుపదిలో x² పదము లోపించిన ఆ ఘన బహుపది యొక్క శూన్యాల మొత్తం ఎంత ?
జవాబు.
0

ప్రశ్న 109.
ax² – x + 6 యొక్క పరావలయం క్రింది వైపుకు తెరచుకొని ఉంటే క్రింది వానిలో ఏది a విలువ కావచ్చును ?
(A) – 1
(B) – 2
(C) – 4
(D) పైవి అన్నీ కావచ్చు
జవాబు.
(D) పైవి అన్నీ కావచ్చు

ప్రశ్న 110.
ఇచ్చిన పటానికి చుట్టుకొలతకు బహుపది p(x) ను కనుగొనుము.

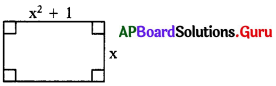
సాధన.
చుట్టుకొలత p(x) = 2 (పొడవు + వెడల్పు)
= 2(x² + 1 + x).
p(x) = 2x² + 2x + 2

ప్రశ్న 111.
క్రింది వానిలో – శూన్యముగా గల బహుపది
(A) 2x – 3
(B) 4x – 6
(C) 81 – 12
(D) పైవి అన్ని
జవాబు.
(D) పైవి అన్ని

ప్రశ్న 112.
2 మరియు -5 లు శూన్యాలుగా గల బహుపది
(A) x² – 3x – 10
(B) x² + 3x – 10
(C) x² – 2x – 5
(D ) x² + 2x + 5.
జవాబు.
(B) x² + 3x – 10

ప్రశ్న 113.
√2 – 1 మరియు √2 + 1 లు శూన్యాలుగా గల వర్గ బహుపది
(A) 2x² – 4√2x + 2
(B) x² + – 2√2 x + 1
(C) 3x² – 6√2 x + 3
(D) పైవన్నీ
జవాబు.
(D) పైవన్నీ

ప్రశ్న 114.
0, 1 మరియు – 1 లు శూన్యాలుగా గల బహుపది
(A) x³ – x² + 1
(B) x³ + x²
(C) x³ – x²
(D) x³ – x
జవాబు.
(D) x³ – x

ప్రశ్న 115.
3x² – 10x + p యొక్క శూన్యాలు ఒకదానికొకటి వ్యుత్ర్కమాలైతే 2 విలువ ఎంత ?
జవాబు.
p = 3

ప్రశ్న 116.
ఇచ్చిన పటంలో ‘0’ వృత్త కేంద్రము, వ్యాసార్ధం OA = x + 1 అయిన వృత్త వైశాల్యంను సూచించు వర్గ బహుపదిని కనుగొనుము.

సాధన.
r = OA = x + 1
∴ వృత్త వైశాల్యం A(x) = πr²
= π(x + 1)²
= π(x² + 2x + 1)
= πx² + 2πx + π

ప్రశ్న 117.
ax³ + bx² + Cx + d ఘన బహుపదిని సూచించా లంటే a, b, c ∈ R మరియు
(A) a = 0
(B) a ≠ 0
(c) b = 0
(D) d ≠ 0
జవాబు.
(B) a ≠ 0

ప్రశ్న 118.
α, β లు బహుపది శూన్యాలు మరియు α + β = 7, αβ = 10గా గల బహుపదుల సమితి
(A) శూన్య సమితి
(B) ఏకమూలక సమితి
(C) అపరిమిత సమితి
(D) నిర్ణయించలేము
జవాబు.
(C) అపరిమిత సమితి

ప్రశ్న 119.
క్రింది వానిలో ఏది సత్యం ?
(A) x² – 49 యొక్క శూన్యాలు 7, -7
(B) x² – 49 యొక్క రేఖాచిత్రం X-అక్షాన్ని (7, 0), (-7, 0) వద్ద ఖండిస్తుంది.
(C) A మరియు B
(D) x – 2 యొక్క శూన్యము – 2
జవాబు.
(C) A మరియు B

ప్రశ్న 120.
రేఖీయ బహుపది యొక్క సాధారణ రూపాన్ని రాయండి.
జవాబు.
ax + b, a ≠ 0

ప్రశ్న 121.
ఘన బహుపది యొక్క సాధారణ రూపాన్ని తెల్పండి.
జవాబు.
ax³ + bx² + cx + d, a ≠ 0

ప్రశ్న 122.
p(x) = x³ – 36x యొక్క రెండు శూన్యాలు 6, – 6 అయిన మూడవ శూన్యం ఎంత ?
సాధన.
p(x) = x³ – 36x యొక్క రెండు శూన్యాలు,
6, – 6, మూడవ శూన్యం γ అనుకొనుము.
శూన్యాల మొత్తం α + β + γ = \(\frac{-b}{a}\)
= 6 + (- 6) + γ = 0
∴ γ = 0
(లేదా) శూన్యాల లబ్ధం ABy = \(\frac{-d}{a}\)
= 6 (-6) γ = \(\frac{0}{1}\) = 0
∴ γ = 0
(లేదా)
x³ – 36x = 0 ⇒ x (x² – 36) = 0
x = 0, x² – 36 = 0
⇒ x² = 36 ⇒ x = √36 = ± 6
∴ శూన్యాలు = 0, 6, – 6
∴ మూడవ శూన్యం = 0

ప్రశ్న 123.
క్రింది పటంలో చూపిన సరళరేఖ \(\overleftrightarrow{X Y}\)ని సూచించు రేఖీయ బహుపది ఏది?

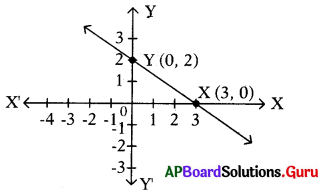
(A) p(x) = x – 3
(B) p(x) = 2 – \(\frac{2}{3}\)x
(C) p(x) = 2 + \(\frac{2}{3}\)x
(D) p(x) = x + 3
సాధన.
(B) p(x) = 2 – \(\frac{2}{3}\)x

వివరణ:
యత్న-దోష పద్ధతిలో సాధించాలి.
(A) p(x) = x – 3 ⇒ y = x – 3, (0, 2) బిందువు గుండా పోదు.
∴ A సరైన సమాధానం కాదు.

(B) p(x) = 2 – \(\frac{2}{3}\)x ⇒ y = 2 – \(\frac{2}{3}\)x,
(0, 2) మరియు (3, 0) బిందువు గుండా. పోతుంది.
∴ B సరైన సమాధానము.

→ క్రింది రేఖాచిత్రంను పరిశీలించి, 124-127 వరకు గల ప్రశ్నలకు సమాధానాలు రాయండి.

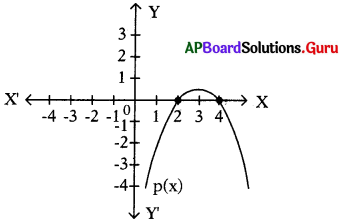
ప్రశ్న 124.
p(x) = ax² + bx + c అయితే క్రింది వానిలో ‘ ఏది సత్యం ?
(A) a > 0
(B) a < 0
(C) a = 0
(D) పైవన్నీ
జవాబు.
(B) a < 0

ప్రశ్న 125.
p(x) యొక్క శూన్యాల మొత్తం ఎంత ?
జవాబు.
2 + 4 = 6

ప్రశ్న 126.
p(x) యొక్క శూన్యాల లబ్ధం ఎంత ?
జవాబు.
2 × 4 = 8

ప్రశ్న 127.
ఈ క్రింది వానిలో ఏది p(x) యొక్క బహుపది ? ,
(A) x² – 6x -8 .
(B) – x² – 6x + 8
(C) – x² + 6x – 8
(D) x² + 6x – 8
జవాబు.
C

ప్రశ్న 128.
x² – 15x + p యొక్క ఒక శూన్యం -5 అయిన ‘p’ విలువ ఎంత?
సాధన.
p(x) = x² – 15x + p యొక్క ఒక శూన్యము = – 5
p(- 5) = 0 ⇒ (- 5)² – 15 (- 5) + p = 0
⇒ 25 + 75 + p = 0 ⇒ p = – 100

ప్రశ్న 129.
p(x) = 9x^a + 10x^b – 7x^c + x ఒక బహుపది. a, b, c యొక్క ఏ విలువలకైన క్రింది వానిలో ఏది p(x) యొక్క ఒక శూన్యం అవుతుంది ?
(A) 1
(B) 0
(C) – 1
(D) పైవన్నీ
జవాబు.
B (∵ స్థిరపదం లేదు కావున ‘O’ ఒక శూన్యము)

ప్రశ్న 130.
p(x) = x^a – 2x^b + 3x^c – 2x అనే బహుపదికి a, b, cఏ విలువలకైనా క్రింది వానిలో ఏది శూన్యము?
(A) 1.
(B) 0.
(C) A మరియు B
(D) -1
సాధన.
C (∵ స్థిరపదం, లేదు కావున ‘O’ ఒక శూన్యము)
p(1) = 1 – 2 + 3 – 2 = 0 కావున 1 ఒక శూన్యము

ప్రశ్న 131.
క్రింది ఏ బహుపది యొక్క గ్రాఫ్ మూలబిందువు గుండా పోవు సరళరేఖను సూచిస్తుంది ?
(A) p(x) = 2x
(B) p(x) = x
(C) p(x) = – x
(D) పైవన్నీ
జవాబు.
(D) పైవన్నీ

(∵ p(x) = y = mx రూపంలో గల బహుపది మూలబిందువు గుండా పోతుంది.)

ప్రశ్న 132.
p(x) = x² + kx + 9 యొక్క ఒక శూన్యము 3 అయిన kవిలువ ఎంత?
(A) – 6
(B) – 3
(C) 6
(D) 3
సాధన.
(A) – 6

వివరణ:
p(x) = x² + kx + 9 యొక్క ఒక శూన్యము 3.
p(3) = (3)² + 3k + 9 = 0
⇒ 3k + 18 = 0 ⇒ k = – 6

ప్రశ్న 133.
p(x) = ax⁴ + bx³ + cx² + dx + e నకు ‘1’ ఒక శూన్యం అయిన క్రింది వానిలో ఏది ఎల్లప్పుడు సత్యం?
(A) a + b + c + d + e = 0
(B) a + c + e = b + d
(C) e = 0
(D ) a = e = 0
సాధన.
(A) a + b + c + d + e = 0

వివరణ:
p(x) = ax⁴ + bx³ + cx² + dx + e ఆ యొక్క
ఒక శూన్యము = 1.
p(1) = a(1)⁴ + b(1)³ + c(1)² + d(1) + e = 0
∴ a + b + c + d + e = 0.

ప్రశ్న 134.
వర్గ బహుపది p(x) గ్రాఫ్ X-అక్షాన్ని OA = OB = 3 యూనిట్లు అవునట్లు ఖండించిన p(x) క్రింది వానిలో ఏది కావచ్చును ?
(A) x² – 9x + 27
(B) x² – 6x
(C) x² – 4x + 4
(D) x² – 9
సాధన.
(D) x² – 9

వివరణ:

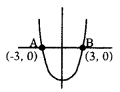
వర్గబహుపది గ్రాఫ్ లో OA = OB = 3.
∴ శూన్యాలు – 3, 3 అవుతాయి.
∴ వర్గ బహుపది = x² – 9.

ప్రశ్న 135.
3x² – 5x + 6 యొక్క శూన్యాల విలోమాలను శూన్యాలుగా గల వర్గ బహుపదిని కనుగొనుము.
సాధన.
3x² – 5x + 6 యొక్క శూన్యాలు α, β అనుకొనుము.
కావలసిన వర్గబహుపది శూన్యాలు \(\frac{1}{\alpha}, \frac{1}{\beta}\).
3x² – 5x + 6 యొక్క శూన్యాలు α, β

Short cut:
ax² + bx + c బహుపది యొక్క శూన్యాలు α, β అయిన \(\frac{1}{\alpha}, \frac{1}{\beta}\) శూన్యాలుగా గల వర్గ బహుపది
= cx² + bx + a
∴ కావలసిన వర్గబహుపది = 6x² – 5x + 3.

ప్రశ్న 136.
ax² + bx + c వర్గ బహుపది యొక్క శూన్యాలు ఒకదానికొకటి వ్యుత్తమాలైతే a = c అని చూపుము.
సాధన.
ax² + bx + c వర్గబహుపది శూన్యాలు ఒకదాని కొకటి వ్యుత్ప్రమాలు.
α ఒక శూన్యం అయిన, \(\frac{1}{\alpha}\) మరొక శూన్యం అవుతుంది.
∴ శూన్యాల లబ్ధం = \(\frac{c}{a}\)
\(\alpha \cdot \frac{1}{\alpha}=\frac{\mathrm{c}}{\mathrm{a}}\) ⇒ 1 = \(\frac{c}{a}\)
∴ a = c

ప్రశ్న 137.
x² – 12x + p యొక్క శూన్యాలు 1 : 2 నిష్పత్తిలో ఉండాలంటే ‘p’ విలువ ఎంత ?
సాధన.
x² – 12x + p యొక్క శూన్యాలు 1 : 2 నిష్పత్తిలో కలవు.
∴ శూన్యాలు α, 2α అనుకొనుము.
శూన్యాల మొత్తం = \(\frac{-b}{a}\)
α + 2α = \(\frac{-(-12)}{1}\)
3α = 12 ⇒ α = 4
శూన్యాల లబ్దం = \(\frac{c}{a}\)
α ∙ 2α = \(\frac{p}{1}\) ⇒ 2α² = 2
2(4)² = p ⇒ p = 32

ప్రశ్న 138.
α, β, γలు శూన్యాలుగా గల ఘన బహుపదిని రాయండి.
సాధన.
x³ – (α + β + γ)x² + (αβ + βγ + γα)x + αβγ

ప్రశ్న 139.
p పరిమాణం గల బహుపదిని (పరిమాణం గల ఒక బహుపదిచే భాగించినపుడు శేషం సున్నా అయిన భాగఫలం యొక్క పరిమాణం ఎంత ?
జవాబు.
p – q

ప్రశ్న 140.
ప్రవచనం-I: x² – 4x + 8 యొక్క శూన్యాల మొత్తం 4.
ప్రవచనం-II: ax²+ bx + c బహుపది యొక్క శూన్యాల లబ్ధం \(\frac{c}{\mathbf{a}}\).
(A) I సత్యం , II అసత్యం
(B) I సత్యం , II అసత్యం , I & II సరైన వివరణ’
(C) I సత్యం, II సత్యం, I & II సరైన వివరణ కాదు
(D) I మరియు II లు రెండూ అసత్యం
జవాబు.
(C) I సత్యం, II సత్యం, I & II సరైన వివరణ కాదు

ప్రశ్న 141.
సమాన శూన్యాలు కలిగిన ఒక వర్గ బహుపదిని రాయండి.
(లేదా)
ఒకే ఒక వాస్తవ శూన్యాన్ని కలిగిన వర్గబహుపదికీ ఉదాహరణనిమ్ము.
సాధన.
ఒకే ఒక శూన్యవిలువ కలిగిన వర్గ బహుపదికి ఉదాహరణ p(x) = (x – 2)² = x² – 4x + 4.

ప్రశ్న 142.
p(x) శూన్యాల మొత్తం సున్న మరియు అందులో ఒక శూన్యం. 4గా గల వర్గ బహుపదిని రాయండి.
సాధన.
α + β = 0 మరియు α = 4 ∴ β = – 4
∴ αβ = – 16
∴ p(x) = x² – 16

ప్రశ్న 143.
ఈ క్రింది వానిలో సత్యమేది ?
(A) ఒక బహుపది యందు స్థిర విలువ లేకుంటే దానికి – సున్న ఒక శూన్య విలువ
(B) శూన్య విలువ వద్ద బహుపది విలువ సున్న
(C) ఒక బహుపది (p, 0) వద్ద X – అక్షాన్ని ఖండించిన దాని శూన్య విలువ ‘p’
(D) పైవన్నీ
జవాబు.
(D) పైవన్నీ

ప్రశ్న 144.
క్రింది వానిలో ఏది. x³ – 6x² + 11x – 6 నకు శూన్యం కాదు?
(A) 0
(B) 1
(C) 2
(D) 3
జవాబు.
(A) 0

(∵ స్థిరపదం – 6 కలదు. కావున ‘O’ ఒక శూన్యము కాదు.)

ప్రశ్న 145.
ax + b బహుపది గ్రాఫ్ X – అక్షాన్ని ఖండించే బిందువు ఏది ?
(A) \(\left(-\frac{b}{a}, 0\right)\)
(B) \(\left(\frac{b}{a}, 0\right)\)
(C) \(\left(0,-\frac{b}{a}\right)\)
(D) \(\left(0, \frac{b}{a}\right)\)
జవాబు.
(A) \(\left(-\frac{b}{a}, 0\right)\)

ప్రశ్న 146.
బహుపదుల భాగహార అల్ గారిథమ్ (భాగహార నియమం)ను రాయండి.
సాధన.
p(x) = g(x) ∙ q(x) + r(x)
r(x) = 0 లేదా r(x) పరిమాణం < g(x) పరిమాణం

ప్రశ్న 147.
p(x) = 2x² – 5x + 6 అయిన p(1) + p(2) విలువను కనుగొనుము.
సాధన.
p(x) = 2x² – 5x + 6
∴ p(1) + p(2) = [2(1)² – 5(1) + 6] + [2(2)² – 5(2) + 6]
= (2 – 5 + 6) + (8 – 10 + 6)
= 3 + 4 = 7

ప్రశ్న 148.
శూన్యాలు సమానంగా గల వర్గ బహుపది యొక్క రేఖాంతం (గ్రాఫ్) చిత్తుపటాన్ని గీయండి.
(లేదా)
b² – 4ac = 0 అయ్యే సందర్భానికి వర్గ బహుపది చిత్తుపటాన్ని గీయండి.
సాధన.

ప్రశ్న 149.
(x – 3) (x – 5) లచే సూచించబడిన బహుపది శూన్యం కానిది
(A) 3
(B) 5
(C) 4
(D) పైవన్నీ
జవాబు.
(C) 4

ప్రశ్న 150.
ఒక రేఖీయ బహుపదికి ఒక శూన్య విలువ ఉండాలంటే అది ……………………….
(A) X- అక్షాన్ని ఖండించాలి
(B) X- అక్షానికి సమాంతరంగా ఉండరాదు
(C) Y-అక్ష్యానికి సమాంతరంగా ఉండవచ్చు
(D) పైవన్ని
జవాబు.
(D) పైవన్ని

ప్రశ్న 151.
రెండు వాస్తవ మూలాలను కలిగిన వరబహుపది యొక్క రేఖాచిత్రం (గ్రాఫ్) యొక్క చిత్తు పటం గీయండి.
(లేదా)
b² – 4ac > 0 అయ్యే సందర్భంలో వర్గబహుపది యొక్క రేఖాచిత్రం యొక్క చిత్తు పటం గీయండి.
సాధన.

ప్రశ్న 152.
3 శూన్యేతర వాస్తవ శూన్య విలువలు కలిగిన బహుపది పరిమాణం ……………
(A) 3 కంటే తక్కువ
(B) 3 లేదా అంతకంటే ఎక్కువ
(C) 3 లేదా అంతకంటే తక్కువ
(D) ఏదీకాదు
జవాబు.
(B) 3 లేదా అంతకంటే ఎక్కువ

ప్రశ్న 153.
x³ – 12x² + px + q నందు రెండు శూన్యాలు సమానం మరియు 3వ శూన్యం 2 అయిన ‘q’ విలువను కనుగొనుము.
సాధన.
x³ – 12x² + px + q యొక్క రెండు శూన్యాలు
సమానం మరియు 3వ శూన్యము 2.
∴ శూన్యాలు α, α, 2 అనుకొనుము. –
శూన్యాల మొత్తం α + α + 2 = \(\frac{-b}{a}\) = \(\frac{-(-12)}{1}\) = 12
∴ 2α + 2 = 12 ⇒ 2α = 10 ⇒ α = 5
శూన్యాల లబ్దం α ∙ α ∙ 2 = \(\frac{-\mathrm{d}}{\mathrm{a}}=\frac{-\mathrm{q}}{1}\)
∴ 5(5)2 = – q ⇒ 50 = – q ⇒ q = – 50

ప్రశ్న 154.
క్రింది వానిలో ఒకే ఒక శూన్యం గల బహుపది యొక్క రేఖాచిత్రం
(A)

(B)

(C)

(D)

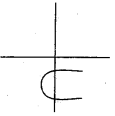
జవాబు.
(B)

ప్రశ్న 155.
x² – px + q నందు గల రెండూ శూన్యాల విలువ సమానం కావలెనన్నా ……………. కావలెను.
(A) p² = q
(B) p² = 2q
(C) p² = 3q
(D) p² = 49
జవాబు.
(D) p² = 49

ప్రశ్న 156.
p(x) = x² – px + 5 అను బహుపది యొక్క p(2) విలువ 3 అయిన ‘p’ విలువ ఎంత?
సాధన.
p(2) = 3 ⇒ (2)² – 2p + 5 = 3
⇒ 9 – 2p = 3
⇒ – 2p = 3 – 9 = – 6 ⇒ p = 3

ప్రశ్న 157.
x² – 5√5 అను బహుపది శూన్యాల మొత్తం ఎంత ?
(A) 5√ 5
(B) 5 + √5
(C) 0
(D) 5 – √5
జవాబు.
(C) 0

ప్రశ్న 158.
క్రింది వానిలో ఏది రెండు వాస్తవ శూన్యాలు కలిగిన వర్గ బహుపది యొక్క రేఖాచిత్రము కావచ్చును?

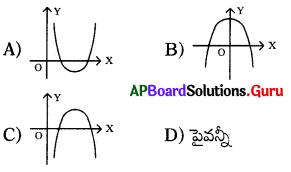
జవాబు.
D

ప్రశ్న 159.
క్రింది వానిలో ఏది α, – α, α శూన్యాలుగా గల బహుపది?
(A) x³ – αx² – α²x – α³
(B) x³ – αx² – α²x + α³
(C) x³ + αx² – α²x – α³
(D) x³ – αx² + α²x – α³
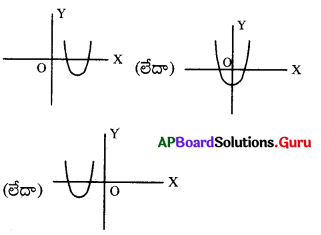
జవాబు.
(B) x³ – αx² – α²x + α³

ప్రశ్న 160.
α, -α శూన్యాలుగా గల వర్గ బహుపదిని రాయండి.
జవాబు.
x² – α²

ప్రశ్న 161.
క్రింది రేఖాచిత్రంను సూచించు వర్గ బహుపదిని కనుగొనుము.

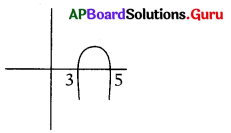
సాధన.
రేఖాచిత్రం సూచించు వర్గబహుపది శూన్యాలు 3, 5.
3, 5 శూన్యాలుగా గల వర్గ బహుపది
= x² – (3 + 5)x + (3) (5)
= x² – 8x + 15

→ గమనిక: α, β లు p(x) = x² – 3x + 2 యొక్క శూన్యాలు.
పై సమాచారం ఆధారంగా 162 – 169 వరకు గల ప్రశ్నలకు జవాబులు రాయండి.

ప్రశ్న 162.
x² – 3x + 2 యొక్క శూన్యాలు కనుగొనుము.
సాధన.
p(x) = x² – 3x + 2
∴ α + β = \(\frac{-b}{a}=\frac{-(-3)}{1}\) = 3
∴ α + β = 3 ………… (1)
∴ αβ = \(\frac{c}{a}\) = 2 ……. (2)
(లేదా)
x² – 3x + 2 యొక్క శూన్యాలు కనుగొని అందు నుండి కూడా సాధించవచ్చును.
x² – 3x + 2 = x² – 2x – x + 2 = 0 .
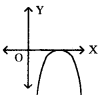
⇒ (x – 2) (x – 1) = 0
శూన్యాలు α = 2, β = 1 గా తీసుకొని సాధించ వచ్చును.

ప్రశ్న 163.
\(\frac{1}{\alpha}+\frac{1}{\beta}\) విలువను కనుగొనుము.
సాధన.
\(\frac{1}{\alpha}+\frac{1}{\beta}\) = \(\frac{\beta+\alpha}{\alpha \beta}\) = \(\frac{3}{2}\)

ప్రశ్న 164.
α2 + β2 విలువను కనుగొనుము.
సాధన.
α² + β² = (α + β)² – 2αβ
= (3)² – 2(2) = 9 – 4 = 5

ప్రశ్న 165.
α – β విలువను కనుగొనుము.
సాధన.
(α – β)² = (α + β)² – 4αβ
= (3)² – 4(2) = 9 – 8 = 1
α – β = √1 = ± 1

ప్రశ్న 166.
α³ + β³ విలువను కనుగొనుము.
సాధన.
α³ + β³ = (α + β)³ – 3αβ(α + β)
= (3)³ – 3(2) (3) = 27 – 18 = 9

ప్రశ్న 167.
α²β + αβ² విలువను కనుగొనుము.
సాధన.
α²β + αβ² = αβ(α + β) = 2(3) = 6

ప్రశ్న 168.
\(\frac{1}{\alpha^{2}}+\frac{1}{\beta^{2}}\) విలువను కనుగొనుము.
సాధన.
\(\frac{1}{\alpha^{2}}+\frac{1}{\beta^{2}}\) = \(\frac{\beta^{2}+\alpha^{2}}{\alpha^{2} \beta^{2}}\) = \(\frac{5}{2^{2}}=\frac{5}{4}\)
(∵ α² + β² = (α + β)² – 2αβ
= (3)² – 2(2) = 9 – 4 = 5)

ప్రశ్న 169.
α³ + β³ = 3αβ(α + β) విలువను కనుగొనుము.
సాధన.
α³ + β³ = 3αβ(α + β)
= (α + β)³ = 3³ = 27.

ప్రశ్న 170.
α, β, γలు x³ + 3x² – x – 2 యొక్క శూన్యాలు అయిన క్రింది వానిని జతపరుచుము.

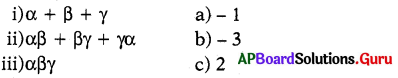
(A) i-a, ii-b, iii-c
(B) i-b, ii-a, iii-c
(C) i-c, ii-a, iii-
(d) i-b, ii-c, iii-a .
జవాబు.
(B) i-b, ii-a, iii-c

ప్రశ్న 171.
p(x) = x³ + 3x² – x – 3 యొక్క రెండు శూన్యాలు – 1 మరియు – 3 అయిన మూడవ శూన్యం ఎంత?
సాధన.
రెండు శూన్యాలు α = – 1, β = – 3
శూన్యాల మొత్తం α + β + γ = \(\frac{-b}{a}\)
(- 1) + (- 3) + γ = \(\frac{-3}{1}\)
– 4 + γ = – 3 ⇒ γ = – 3 + 4 = 1
(లేదా)
శూన్యాల లబ్ధం αβγ = \(\frac{-d}{a}\)
(-1) (-3)γ = \(\frac{-(-3)}{1}\)
γ = 1
∴ మూడవ శూన్యము = 1

ప్రశ్న 172.
ఘనబహుపది యొక్క రేఖాచిత్రము ‘చిత్తుపటాన్ని గీయండి.
జవాబు.

ప్రశ్న 173.
p(x) = 2x + 4 యొక్క రేఖాచిత్రం (గ్రాఫ్)ను గీయండి.
సాధన.
p(x) = y = 2x + 4

ప్రశ్న 174.
రేఖీయ బహుపది యొక్క చిత్తుపటాన్ని గీయండి.
జవాబు.

ప్రశ్న 175.
ప్రవచనం P: ax² + bx + c వర్గ బహుపది శూన్యాల మొత్తం \(\frac{c}{a}\)కి సమానము.
ప్రవచనం Q: ఘన బహుపది
ax³ + bx² + cx + d యొక్క శూన్యాల లబ్దము –\(\frac{b}{a}\) కి సమానము.
(A) P సత్యం, Q అసత్యం
(B) P అసత్యం, Q సత్యం
(C) P, Q లు రెండూ అసత్యం
(D) P, Q లు రెండూ సత్యం
జవాబు.
(C) P, Q లు రెండూ అసత్యం

గమనిక: p(x) = ax² + bx + c వర్గ బహుపదికి క్రింది సందర్భాలలో 176-179 వరకు గల ప్రశ్నలకు సమాధానాలు రాయండి.

ప్రశ్న 176.
a < 0 మరియు రెండు వాస్తవ శూన్యాలు గల సందర్భంలో p(x) రేఖాచిత్రము చిత్తుపటం గీయండి.
జవాబు.

ప్రశ్న 177.
a < 0 మరియు సమాన వాస్తవ శూన్యాలు కలిగిన సందర్భం యొక్క రేఖాచిత్రము చిత్తుపటం గీయండి.
జవాబు.

ప్రశ్న 178.
a < 0 మరియు వాస్తవ శూన్యాలు లేనటువంటి సందర్భం యొక్క రేఖాచిత్రము (గ్రాఫ్) చిత్తుపటం గీయండి. జవాబు.

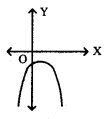
ప్రశ్న 179.
a > 0 మరియు వాస్తవ శూన్యాలు లేనటువంటి ‘ సందర్భంనకు రేఖాచిత్రము (గ్రాఫ్) చిత్తుపటం గీయండి.
జవాబు.

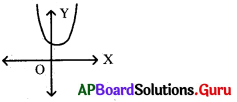
ప్రశ్న 180.
sin 90°, tan² 60° విలువలను శూన్యాలుగా గల వర్గబహుపదిని కనుగొనుము.
సాధన.
sin 90° = 1, tan² 60° = (√3)² = 3
∴ 1, 3 శూన్యాలుగా గల వర్తబహుపది
p(x) = x² – (1 + 3)x + 1(3)
= x² – 4x + 3

→ గమనిక: ABCD ఒక చతురస్రం మరియు దాని భుజము (x + 3) యూ॥ అయిన క్రింది 181-183 , ప్రశ్నలకు సమాధానాలు రాయండి.

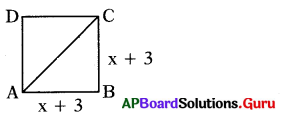
ప్రశ్న 181.
చతురస్రం యొక్క చుట్టుకొలతను సూచించు బహుపదిని కనుగొనుము.
సాధన.
చుట్టుకొలత p(x) = 4s
= 4(x + 3) = 4x + 12

ప్రశ్న 182.
చతురస్రం ABCD వైశాల్యాన్ని సూచించే బహుపదిని కనుగొనుము.
సాధన.
వైశాల్యము A(x) = s²
= (x + 3)² = x² + 6x + 9

ప్రశ్న 183.
కర్ణం AC పొడవును సూచించు రేఖీయ బహుపదిని రాయండి.
సాధన.
కర్ణము D(x) = √2s = √2 (x + 3)
= √2 x + 3√2

ప్రశ్న 184.
“ఒకే శూన్య విలువలను కలిగిన అనేక వర్గబహుపదులు/ బహుపదులు వ్యవస్థితం” అవుతాయని రంజని, కాదు ఏకైకంగా వ్యవస్థితం అవుతుందని హరి అంటున్నారు. ఎవరి వాదనతో నీవు ఏకీభవిస్తావు ? నీ సమాధానాన్ని సమర్థించుము.
సాధన.
రంజని వాదనతో ఏకీభవిస్తాను.
కారణం: α, β శూన్యాలుగా గల వర్గబహుపది
= k(x² – (α + β) x + αβ); k ∈ R
k యొక్క వేర్వేరు విలువలకు వేర్వేరు బహుపదులు వ్యవస్థితం అవుతాయి.

ప్రశ్న 185.
క్రింది బహుపదుల రేఖాచిత్రాలను, బహుపదుల వివిధ సందర్భాలకు జతపరుచుము.

(A) i-e, ii – d, iii – a, iv – b
(B) i – c, ii – d, iii – a, iv – b
(C) i-e, ii – a, iii – b, iv – C
(D) i – c, ii-e, iii – d, iv – a
జవాబు.
(B) i – c, ii – d, iii – a, iv – b

ప్రశ్న 186.
α, β, γలు బహుపది px³ + qx² + rx + s యొక్క శూన్యాలైన, క్రింది వాటిలో సరైన మ్యాచింగ్ ఏది?

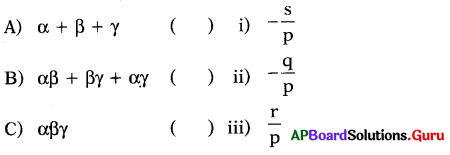
(a) A(i), B(ii), C(iii)
(b) A(ii), B(iii), C(i)
(c) A(iii), B(i), C(ii),
(d) A(ii), B(i), C(iii)
జవాబు.
(b) A(ii), B(iii), C(i)

ప్రశ్న 187.
3x – 2 బహుపది యొక్క శూన్యవిలువ ఏమిటి ?
సాధన.
f(x) = 3x – 2; f(x) = 0
3x – 2 = 0 ⇒ 3x = 2 ⇒ x = \(\frac{2}{3}\)

ప్రశ్న 188.
– \(\frac{\mathbf{k}}{\mathbf{a}}\) శూన్యముగా గల బహుపదిని చలరాశి ‘X’ లో వ్రాయుము.
సాధన.
x – \(\left(-\frac{k}{a}\right)\) = 0 ⇒ x + \(\frac{\mathrm{k}}{\mathrm{a}}\) = 0
⇒ ax + k = 0
∴ పరిమాణము ‘1’ మరియు ‘x’ చలరాశిగా గల
ax + k = 0 బహుపది శూన్య విలువ –\(\frac{\mathrm{k}}{\mathrm{a}}\)