Practice the AP 10th Class Maths Bits with Answers 2nd Lesson సమితులు on a regular basis so that you can attempt exams with utmost confidence.
AP Board 10th Class Maths Bits 2nd Lesson సమితులు
ప్రశ్న1.
A, B లు వియుక్త సమితులైతే కింది వానిలో ఏది సత్యం?
A) n(A ∪ B) = n(A) + n(B)
B) A ∩ B = Φ
C) A & B
D) n(A ∪ B) = n(A) = n(B)
జవాబు :
C) A & B
ప్రశ్న2.
n(A) = 5, n(B) = 7 మరియు ACB అయిన n(A ∪ D) విలువ ఎంత ?
జవాబు :
7
ప్రశ్న3.
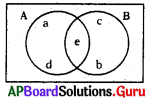
క్రింది వెన్ చిత్రంలో షేర్ చేసిన ప్రాంతాన్ని సూచించు సమితిని రాయండి.
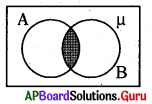
జవాబు :
A ∩ B
ప్రశ్న4.
A ⊂ B అయితే A – B = ________
A) A
B) B
C) μ
D) Φ
జవాబు :
D) Φ
ప్రశ్న5.
చంద్రునిపై నివసించు మనుజుల సమితి ________
A) శూన్యసమితి
B) విశ్వసమితి P
C) పరిమిత సమితి
D) అపరిమిత సమితి
జవాబు :
A) శూన్యసమితి
![]()
ప్రశ్న6.
క్రింద ఇవ్వబడిన వెన్ చిత్రములో క్రింది వానిలో ఏది సత్యం ?
A) A ∪ B = Φ
B) A ∪ B = μ
C) A ∩ B = μ
D) A ∩ B = Φ
జవాబు :
D) A ∩ B = Φ
ప్రశ్న7.
ఈ క్రింది వానిలో పరిమిత సమితికి ఉదాహరణ ________
A) {x/x ∈N మరియు x2 = 9}
B) 2, 3 ల మధ్య గల అకరణీయ సంఖ్యల సమితి
C) సరి ప్రధాన సంఖ్య అన్ని గుణిజాల సమితి
D) అన్ని బేసి ప్రధాన సంఖ్యల సమితి
జవాబు :
A) {x/x ∈N మరియు x2 = 9}
ప్రశ్న8.
Φ సమితి యొక్క ఉప సమితుల సంఖ్య.
జవాబు :
1
ప్రశ్న9.
ఈ క్రింది ప్రవచనాలలో ఏది అసత్యము ?
A) ప్రతీ సమితి దానికదే ఉపసమితి.
B) శూన్య సమితి ప్రతీ సమితికి ఉపసమితి.
C) రెండు వియుక్త సమితుల ఛేదనము ఒక శూన్య సమితి.
D) ఒక అపరిమిత సమితి యొక్క కార్డినల్ సంఖ్య సున్న.
జవాబు :
D) ఒక అపరిమిత సమితి యొక్క కార్డినల్ సంఖ్య సున్న.
ప్రశ్న10.
n(A) = 12, n(A ∩ B) = 5 అయితే n(A – B) విలువ ఎంత ?
జవాబు :
n(A – B) = n(A) – n(A ∩ B)
= 12 – 5 =7.
ప్రశ్న11.
A = {x:x అనేది HEADMASTER పదంలోనీ అక్షరం} అయిన ఈ సమితికి సరియగు జాబితా రూపం.
A) A = {h, e, a, d, m, a, s, t, e, r}
B) A = {h, e, a, d, m, s, t, r}
C) A = {h, e, a, d, M, S, t, e, r}
D) A = {h, e, a, d, m, a, s, t, r}
జవాబు :
B) A = {h, e, a, d, m, s, t, r}
ప్రశ్న12.
{x : X అనేది ప్రధాన సంఖ్య మరియు 6 ను భాగిస్తుంది} సమితి యొక్క రోస్టర్ రూపాన్ని రాయండి.
జవాబు :
{2, 3}
ప్రశ్న13.
A = {1, 2, 3, 4} అయిన A యొక్క ఉపసమితుల – సంఖ్య ఎంత ?
జవాబు :
16.
ప్రశ్న14.
A = {x : X అనేది EXAMINATION పదంలోని అక్షరం} అయిన ఈ సమితికి జాబితా రూపం.
A) A = {e, x, m, i, n, a, t, 0, s}
B) A = {e, x, m, i, n, a, t, 0}
C) A = {e, x, m, a, i, n, t, s}
D) D = {e, x, m, i, n, t, 0}
జవాబు :
B) A = {e, x, m, i, n, a, t, 0}
ప్రశ్న15.
ఈ క్రింది వెన్ చిత్రం సూచించునది.
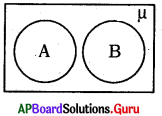
A) A ∩ B = Φ
B) A, B లు వియుక్త సమితులు
C) A మరియు B
D) A – B = Φ
జవాబు :
C) A మరియు B
ప్రశ్న16.
A ⊂ B, n(A) = 12, n(B) = 20 అయిన n(B- A) విలువ ఎంత ?
జవాబు :
A⊂B అయిన
n(B – A) = n(B) – 1(A) = 20 – 12 = 8
![]()
ప్రశ్న17.
A ⊂ B, n(A) = 4 మరియు n(B) = 6 అయిన n(A ∪ B) =
జవాబు :
A c B అయిన A ∪ B = B
∴ n(A ∪ B) = n(B) = 6
ప్రశ్న18.
n(A) = 8, n(B) = 3, n(A ⊂ B) = 2 అయిన n(A ∪ D) ని కనుగొనుము.
జవాబు :
n(A ∪ B) = n(A) + n(B) – n(A ∩ B)
= 8 + 3 – 2 = 9
ప్రశ్న19.
ఇచ్చిన పటంలోని షేర్ చేసిన ప్రాంతంను. సూచించునది.
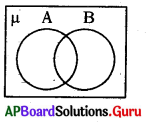
A) A – B.
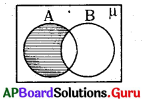
B) B – A
C) μ – B
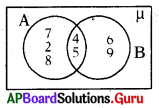
D) A ∪ B
జవాబు :
C) μ – B
ప్రశ్న20.
A = {x: x2 – 16 = 0, x ∈ R} మరియు
B= {x: x2 – 5x + 6 = 0, x ∈ R}, అయిన A ∪ B
A) ఏకమూలక సమిల
B) అనంత సమితి
C) శూన్య సమితి
D) పరిమిత సమితి
జవాబు :
D) పరిమిత సమితి
ప్రశ్న21.
క్రింది వానిని వాని యొక్క గుర్తులకు జతపరచండి.
| i) శూన్యసమితి | a) μ |
| ii) విశ్వసమితి | b) ⊆ |
| iii) ఉపసమితి | c)Φ |
A) i-c, ii-a, iii-b,
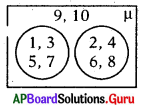
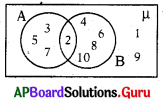
B) i-c, ii-b, iii-a
C) i-a, ii-b, iii-c
D) i-a, ii-c, iii-b
జవాబు :
A) i-c, ii-a, iii-b,
ప్రశ్న22.
A, Bకి ఉపసమితి అవునట్లు A, B సమితులకు ఒక ఉదాహరణను ఇవ్వండి.
జవాబు :
A = {2, 3}. B = {1, 2, 3, 4,}
ప్రశ్న23.
V = {x/x అనేది ఆంగ్ల భాషలోని అచ్చు} సమితిని రోస్టర్ రూపంలో రాయండి.
జవాబు :
V = {a, e, i, 0, u}
ప్రశ్న24.
{1, 8, 27, 64, 125} యొక్క సమితి నిర్మాణ రూపంను రాయండి.
జవాబు :
{x : x = n3, n ∈ N, n < 6} లేదా
{x: x అనేది 126 లోపు గల ఘనసంఖ్య}
25.
{x : x అనేది 1260 యొక్క ప్రధాన కారణాంకం} యొక్క రోస్టర్ రూపంను రాయండి.
జవాబు :
{2, 3, 5, 7} (∵ 1260 = 22 × 32 × 5 × 7)
ప్రశ్న26.
{x: x అనేది ఒక సహజ సంఖ్య మరియు x2 ≤ 36} యొక్క రోస్టర్ రూపంను తెల్పండి.
జవాబు :
{1, 2, 3, 4, 5, 6}
ప్రశ్న27.
P= {x : X అనేది -3.5 మరియు 2.7 ల మధ్య గల పూర్ణసంఖ్య} యొక్క జాబితా రూపం ఏది ?
జవాబు :
{-3, -2, -1, 0, 1, 2}
ప్రశ్న28.
ప్రవచనం-I : n(A) + n(B) = n(A ∪ B) + n (A ∩ B)
ప్రవచనం-II : A ∩ B = 6 అయిన A, B లు వియుక్త సమితులు.
A) I సత్యం, II అసత్యం
B) I సత్యం, II సత్యం
C) I అసత్యం, II సత్యం
D) I అసత్యం, II అసత్యం
జవాబు :
B) I సత్యం, II సత్యం
ప్రశ్న29.
SCHOOL పదంలోని అక్షరాలతో ఏర్పడే సమితి
A) {S, C, H, 0, L}
B) {C, H, L, 0, S}
C) {S, 0, L, H, C}
D) పైవన్నీ
జవాబు :
D) పైవన్నీ
ప్రశ్న30.
A = {x: x అనేది 36 యొక్క కారణాంకము} క్రింది వానిలో A సమితికి చెందని మూలకం ఏది ?
A) 12
B) 6
C) 5
D) 4
జవాబు :
C) 5
![]()
ప్రశ్న31.
శూన్యసమితి యొక్క గుర్తును తెల్పండి.
జవాబు :
Φ
ప్రశ్న32.
K = {5, 3, 2, 1} అయిన క్రింది వానిలో అసత్యం ?
A) 5 ∈ K
B) {5} ∈ K
C) {5} ∈ K.
D) {1, 5} ∈ K
జవాబు :
B) {5} ∈ K
ప్రశ్న33.
క్రింది వానిలో సత్య వాక్యం
A) 5 ∈ {సరిసంఖ్యలు}
B) [latex]\frac{8}{11}[/latex] ∈ {అకరణీయ సంఖ్యలు}
C) -8 ∈ {సహజసంఖ్యలు}
D) √5 ∈ {పూర్ణసంఖ్యలు}
జవాబు :
B) [latex]\frac{8}{11}[/latex] ∈ {అకరణీయ సంఖ్యలు}
ప్రశ్న34.
A = {2, 4, 6, 8, 10} అయిన క్రింది సమితులలో ఏది Aని సూచించదు ?
A) {x ; x = 2n, n ∈ N మరియు n<5}
B) {x: x అనేది 11 కన్నా తక్కువైన సరి సహజసంఖ్య }
C) {x : x = 2n, n ∈ N మరియు n < 5}
D) {x : x = 2n, n ∈ W మరియు 1 ≤ n ≤ 5}
జవాబు :
C) {x : x = 2n, n ∈ N మరియు n < 5}
ప్రశ్న35.
{1, 4, 9, 16, 25…., 81, 100} యొక్క సమితి నిర్మాణ రూపంను రాయండి.
జవాబు :
{x : x అనేది 100 వరకు గల వర్గ సంఖ్య }
(లేదా)
{x: x = n2, x ∈ N మరియు x < 11}
ప్రశ్న36.
“ASSOCIATE” లోని అక్షరాల సమితి యొక్క రోస్టర్ రూపాన్ని రాయండి.
జవాబు :
{A, S, 0, C, I, T, E}
ప్రశ్న37.
క్రింది వానిలో శూన్యసమితి
A) {x : x, 2 కన్నా పెద్దదైన సరి ప్రధానాంకము}
B) {x : x సరి ప్రధానసంఖ్య}
C) {x : x ఒక సహజసంఖ్య మరియు 1 < x < 3}
D) {x : x2 = 4 మరియు x సహజసంఖ్య }
జవాబు :
A) {x : x, 2 కన్నా పెద్దదైన సరి ప్రధానాంకము}
ప్రశ్న38.
{2} ను సూచించు సమితి నిర్మాణ రూపం
A) {x : x సరి ప్రధానాంకము}
B) {x : 1 C) {x : x2 = 4, x ఒక సహజసంఖ్య }
D) పైవన్నీ
జవాబు :
D) పైవన్న
ప్రశ్న39.
క్రింది వానిలో పరిమిత సమితి
A) {x: x = 2n, n ∈ N}
B) {x : x అనేది 2 యొక్క కారణాంకం}
C) {x : x = 2n, n ∈ N}
D) పైవన్నీ
జవాబు :
B) {x : x అనేది 2 యొక్క కారణాంకం}
ప్రశ్న40.
క్రింది వానిలో అపరిమిత సమితి
A) 3 మరియు 8 ల మధ్యగల పూర్ణసంఖ్యల సమితి
B) 2 మరియు 3 ల మధ్యగల అకరణీయ సంఖ్యల సమితి
C) 1 మరియు 50 ల మధ్యగల ప్రధానాంకముల సమితి
D) 100 కన్నా తక్కువైన సహజసంఖ్యల సమితి
జవాబు :
B) 2 మరియు 3 ల మధ్యగల అకరణీయ సంఖ్యల సమితి
ప్రశ్న41.
క్రింది సమితులలో ఏది {9} ను సూచించదు?
A) {x/x ఒక అంకె సంఖ్యలలో పెద్దది}
B) {x/x + 1 = 10}
C) {x/ √x = 3, x ∈ N}
D) {x/x – 1 = 10}
జవాబు :
D) {x/x – 1 = 10}
ప్రశ్న42.
క్రింది వానిలో పరిమిత సమితి.
A) {x : x ∈ N మరియు (x – 1) (x – 2) = 0}
B) {x: n ∈ N మరియు x = 2n + 1}
C) {x : x ∈ Z మరియు x2 ≥ 24}
D) {x : x ∈ Z మరియు x <4}
జవాబు :
A) {x : x ∈ N మరియు (x – 1) (x – 2) = 0}
ప్రశ్న43.
C = {1, 2, 3, 5} అయిన n (C) విలువ ఎంత ?
జవాబు :
n(C) = 4
ప్రశ్న44.
n (Φ) విలువను తెల్పండి.
జవాబు :
n (Φ) = 0
ప్రశ్న45.
A = {6, 7, 8, 9, 10},
B = {8, 9, 10},
C = {a, b} అయిన క్రింది వానిలో ఏది సత్యం ?
A) n(A) < n(B)
B) n(A) = n(B) + n(C)
C) n(A) = n(B) – n(C)
D) n(B) < n(C)
జవాబు :
B) n(A) = n(B) + n(C)
ప్రశ్న46.
B = {x: x + 7 = 7x, x ∈ Z} అయిన n(B) విలువ ఎంత ?
జవాబు :
x + 7 = 7x ⇒ 7 = 6x ⇒ [latex]\frac{7}{6}[/latex] = x ∈ Z
ప్రశ్న47.
క్రింది వానిలో కార్డినల్ సంఖ్య 2గా గల సమితి ఏదీ?
A) {x : x2 = 4 మరియు x పూర్ణసంఖ్య }
B) {x : x ≤ 5 మరియు x సహజసంఖ్య }
C) {x : x అనేది సరి ప్రధానసంఖ్య }
D) {x : x ∈ N మరియు x < 5, ముయు x > 8}
జవాబు :
A) {x : x2 = 4 మరియు x పూర్ణసంఖ్య }
ప్రశ్న48.
క్రింది వానిలో కార్డినల్ సంఖ్యను నిర్ణయించలేని సమితి ఏది ?
A) 6 యొక్క కారణాంకాల సమితి
B) ఆంగ్లభాషలోని అక్షరాల సమితి
C) 100 మరియు 1000 ల మధ్య గల 5 గుణిజాల సమితి
D) X – అక్షానికి సమాంతరంగా ఉండే రేఖల సమితి
జవాబు :
D) X – అక్షానికి సమాంతరంగా ఉండే రేఖల సమితి
ప్రశ్న49.
A = {1, 2, 3, 4}, B = {2, 4, 6, 8, 10} అయిన n(A ∩ B)ని కనుగొనుము.
జవాబు :
A ∩ B = {2, 4}
![]()
ప్రశ్న50.
A = {2, 4, 6, 8, 10}, B = {1, 2, 3, 4, 5, 6} అయిన n(B – A) ని కనుగొనుము.
జవాబు :
B – A = {1, 3, 5}
n(B – A) = 3
ప్రశ్న51.
ఉపసమితిని సూచించు గుర్తును రాయండి. .
జవాబు :
⊂
ప్రశ్న52.
A ⊂ B అయిన A ∪ B = ________
జవాబు :
Φ
ప్రశ్న53.
A ⊂ B అయిన A ∩ B = ________
జవాబు :
A
ప్రశ్న54.
వెన్ చిత్రం సూచించునది.
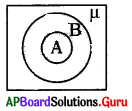
A) A ⊂ B
B) B ⊂ A
C) A, B లు వియుక్త సమితులు
D) µ ⊂ B
జవాబు :
A) A ⊂ B
ప్రశ్న55.
A = {2, 3, 4, 5, 6} అయిన Aకి గల ఉపసమితుల సంఖ్య ఎంత?
జవాబు :
32
ప్రశ్న56.
P= {1, 5}, Q = {2, 4, 6}, R = {1, 2, 3, 4, 5, 6}, S = {3, 5, 6} అయిన సందర్భంలో విశ్వ సమితి ఏది ?
A) P
B) Q
C) R
D) S
జవాబు :
C) R
ప్రశ్న57.
A = {x : x అనేది ASSASSINATION పదములోని అక్షరం}, B = {x : x అనేది STATION పదంలోని అక్షరం} అయిన క్రింది వానిలో ఏది సత్యం?
A) [latex]\mathrm{A} \not \subset \mathrm{B}[/latex]
B ) A ≠ B
C) A = B
D) A ∩ B = 0
జవాబు :
C) A = B
ప్రశ్న58.
క్రింది వానిలో ఏది సత్యం ?
A) Φ = {0}
B) Φ = { }
C) n (Φ) = 1
D) Φ = 0
జవాబు :
B) Φ = { }
ప్రశ్న59.
A = {5, 10, 20, 40} అయిన A కి ఉపసమితి కానిది
A) 4
B) {5, 10, 40}
C) {15, 10}
D) {5, 10, 20, 40}
జవాబు :
C) {15, 10}
ప్రశ్న60.
A ∩ B = ________
A) {x: x ∈ A మరియు x ∈ B}
B) {x : x ∈ A లేదా x ∈ B}
C) {x : x ∈ A మరియు x ∉ B}
D) {x : x ∉ A లేదా x ∉ B}
జవాబు :
A) {x: x ∈ A మరియు x ∈ B}
ప్రశ్న61.
షేడ్ చేసిన ప్రాంతం సూచించునది ”
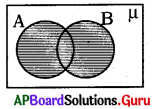
A) A – B
B) B – A
C) A ∪ B
D) A ∩ B
జవాబు :
C) A ∪ B
ప్రశ్న62.
వెన్ చిత్రానికి సంబంధించి క్రింది వానిలో ఏది సత్యం ?
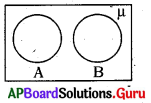
A) A ∪ B = A
B) A ∩ B = Φ
C) A – B = Φ
D) A ∪ B = B
జవాబు :
B) A ∩ B = 0
ప్రశ్న63.
షేడ్ చేసిన ప్రాంతం సూచించునది
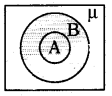
A) A ∪ B = B
B) A ∪ B = A
C) A ⊂ B
D) A మరియు C
జవాబు :
D) A మరియు C
![]()
ప్రశ్న64.
సాధారణంగా విశ్వసమితిని సూచించుటకు ఉపయోగించే వెన్ చిత్రం
![]()
జవాబు :
D
ప్రశ్న65.
A = {5, 6, 7, 8}, B = {7.8, 9, 10} అయిన A ∩ Bని కనుగొనుము.
జవాబు :
A ∩ B = {7, 8}
ప్రశ్న66.
A – B = ____________
A) {x : x ∈A మరియు x ∈ B}
B) {x : x ∈ A మరియు x ∉ B}
C) {x : x ∈ A లేదా x ∈ B}
D) {x : x # A మరియు x ∈ B}
జవాబు :
B) {x : x ∈ A మరియు x ∉ B}
ప్రశ్న67.
A – Bకి వియుక్త సమితి
A) A ∪ B
B) B – A
C) A
D) పైవన్నీ
జవాబు :
B) B – A
ప్రశ్న68.
వెన్ చిత్రం నుండి A సమితిని రాయండి.
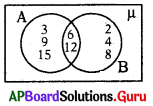
జవాబు :
A = {3, 6, 9, 12, 15}
ప్రశ్న69.
A, Bలు శూన్యసమితులు కాకపోతే A – B, B – A మరియు A ∩ Bలు
A) వియుక్త సమితులు
B) సమసమితులు
C) ఒకదానికొకటి ఉపసమితులు
D) పైవేవీ కావు
జవాబు :
A) వియుక్త సమితులు
ప్రశ్న70.
A ∪ Φ = ________
జవాబు :
A
ప్రశ్న71.
A = {1, 2, 3, 4, 5}, B = {4, 5, 6, 7} అయిన A – B ని కనుగొనుము.
జవాబు :
A – B= {1, 2, 3, 4, 5} – {4, 5, 6, 7}
= {1, 2, 3}
→ ఇచ్చిన వెన్ చిత్రాన్ని పరిశీలించి 72, 73 ప్రశ్నలకు – సమాధానాలు రాయండి.
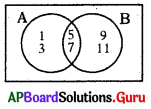
ప్రశ్న72.
B- A సమితిని రాయండి.
జవాబు :
B – A = {9, 11}
ప్రశ్న73.
A ∩ B సమితిని రాయండి.
జవాబు :
A ∩ B = {5, 7}
ప్రశ్న74.
n(A) = 5, n(B) = 4, n (A ∩ B) = 3 అయిన n(A ∪ B).ని కనుగొనుము.
జవాబు :
n(A ∪ B) = n(A) + n(B) – n(A ∩ B)
= 5 + 4 -3 = 6
ప్రశ్న75.
A ∩ B = Φ అయిన క్రింది వానిలో ఏది సత్యం ?
A) A, B లు వియుక్త సమితులు
B) A ≠ Φ మరియు B = Φ
C) A = Φ మరియు B ≠ Φ
D) పైవన్నీ
జవాబు :
D) పైవన్నీ
ప్రశ్న76.
A ∪ B = Φ కి సంబంధించి క్రింది వానిలో ఏది సత్యం ?
A) A = Φ మరియు B ≠ Φ
B) A = Φ మరియు B = Φ
C) A ≠ Φ మరియు B = Φ
D) పైవన్నీ
జవాబు :
B) A = Φ మరియు B = Φ
ప్రశ్న77.
ఒక మూలకం సమితికి చెందుతుంది అని తెలుపుటకు ఉపయోగించే గుర్తును తెల్పండి.
జవాబు :
∈
![]()
ప్రశ్న78.
క్రింది వానిని జతపరుచుము :
| i) A∪ B | a) {x : x ∈ A మరియు x ∈ B} |
| ii) A ∩ B | b) {x : x ∈ A మరియు x ∈ B} |
| iii)A – B | c) {x : x ∈ A మరియు x ∈ B} |
| iv) B – A | d) {x: x ∈ A లేదా x ∈ B} |
A) i-a, ii-b, iii-d, iv-c
B) i-d, ii-a, iii-c, iv-b
C) i-d, ii-b, iii-a, iv-c
D) i-b, ii-d, iii-c, iv-a
జవాబు :
C) i-d, ii-b, iii-a, iv-c
ప్రశ్న79.
విశ్వసమితికి గుర్తును రాయండి.
జవాబు :
µ
ప్రశ్న80.
a ∈ A ⇒ a ∈ B అయిన
A) A ⊂ B
B) B ⊂ A
C) A = B
D) A = B = Φ
జవాబు :
A) A ⊂ B
ప్రశ్న81.
A అపరిమిత సమితి అయితే n(A) విలువ ఎంత ?
జవాబు :
నిర్ణయించలేము.
ప్రశ్న82.
A, B లు రెండు సమితులైన A ∪ Bని వెన్ చిత్రంలో చూపండి.
జవాబు :
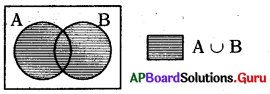
ప్రశ్న83.
A ∩ Bని సూచించు వెన్ చిత్రాన్ని గీయండి.
జవాబు :
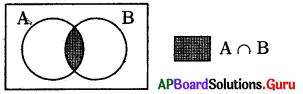
ప్రశ్న84.
A – B ని వెన్ చిత్రంలో చూపండి.
జవాబు :
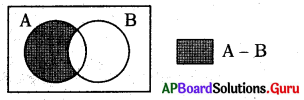
ప్రశ్న85.
A = {1, 2, 3, 4} అయిన క్రింది వానిలో ఏది అసత్యం ?
A) Φ ⊂ A
B) n(A) = 4;
C) A కి, గల ఉపసమితుల సంఖ్య 16
D) {3, 6} ⊂ A
జవాబు :
D) {3, 6} ⊂ A
ప్రశ్న86.
A = {2, 6} అయిన A కి గల ఉపసమితుల సంఖ్య ?
జవాబు :
4.
ప్రశ్న87.
A ⊂ B అయి B ⊂ C అయిన క్రింది వానిలో ఏది సత్యం ?
A) [latex]\mathrm{A} \not \subset \mathrm{C} .[/latex]
B) A ⊂ C
C) B ⊂ A
D) C ⊂ B
జవాబు :
B) A ⊂ C
ప్రశ్న88.
A = {x : x అనేది ASSOCIATION పదంలోని అక్షరం }
B = {x: X అనేది ASSOCIATE పదంలోని అక్షరం}
అయిన క్రింది వానిలో ఏది సత్యం ?
A) A ⊂ B
B) B ⊂ A
C) A ∪ B = Φ
D) పైవన్న
జవాబు :
B) B ⊂ A
ప్రశ్న89.
A = {x : x అనేది ASSISTANCE పదంలోని అక్షరం}
B= {x : x అనేది ASSISTANT పదంలోని అక్షరం} అయిన
A) A ∪ B =A
B) A ∩ B = B
C) B ⊂ A
D) పైవన్నీ
జవాబు :
D) పైవన్నీ
![]()
ప్రశ్న90.
A = B అయిన
i) A ⊂ B
ii) B ⊂ A
iii) n(A) = n(B) లలో ఏది సత్యం ?
A) i మాత్రమే సత్యం
B) i, ii లు మాత్రమే సత్యం
C) i, ii, iii లు సత్యం
D) i, iii మాత్రమే సత్యం
జవాబు :
C) i, ii, iii లు సత్యం
ప్రశ్న91.
A = {సహజసంఖ్యల సమితి}, B = {ప్రధాన సంఖ్యల సమితి} అయిన A ∩ B =
A) A
B) B
C) Φ
D) A ∪ B
జవాబు :
B) B
ప్రశ్న92.
A = {సరి సహజసంఖ్యల సమితి}, B = {ప్రధాన సంఖ్యల సమితి} అయిన A ∩ B ని కనుగొనుము.
జవాబు :
A = {2, 4, 6, 8, ….}; B = {2, 3, 5, 7, ….}.
A ∩ B = {2}
ప్రశ్న93.
A = {x : x అనేది 6300 యొక్క ప్రధాన కారణాంకం} అయిన A సమితికి చెందని వారు,
A) 11
B) 3
C) 5
D) 2
జవాబు :
A) 11
ప్రశ్న94.
ఏదైనా ఒక మూలకం సమితికి చెందదు అని తెలుపుటకు ఉపయోగించే గుర్తును రాయండి.
జవాబు :
∉
ప్రశ్న95.
{x: x ∈ N మరియు 0 జవాబు :
{1, 2, 3, 4}
ప్రశ్న96.
A = {3, 5, 7, 9}, B = {2, 4, 6, 8} అయిన
క్రింది వానిలో సత్య ప్రవచనాలు ఏవి ?
I : A, Bలు వియుక్త సమితులు
II : A = B
III : n(A) = n(B)
IV : A – B = B
A) I, II, IV
B) I, III
C) II, IV
D) II, III, IV.
జవాబు :
B) I, III
ప్రశ్న97.
B ⊂ A అయ్యే సందర్భాన్ని వెన్ చిత్రంలో చూపండి. జ.
జవాబు :

ప్రశ్న98.
2 మరియు 3ల మధ్యగల పూర్ణసంఖ్యల సమితిని రాయండి.
జవాబు :
Φ (∵ 2, 3 ల మధ్య పూర్ణసంఖ్యలు లేవు)
ప్రశ్న99.
క్రింది వెన్ చిత్రం నుండి క్రింది వానిలో ఏది అసత్యం ?
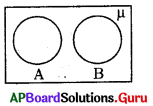
A) A ∩ B = 0
B) A – B = A
C) B – A = B
D) A ∪ B = A
జవాబు :
D) A ∪ B = A
ప్రశ్న100.
A = {1, 2, 3, 4, 5} మరియు A, B లు సమసమితులైతే n(B) విలువ ఎంత ?
జవాబు :
n(A) = n(B) = 5
ప్రశ్న101.
A = {x, y, z} అయిన Aకి గల ఉపసమితుల సంఖ్య ఎంత ?
జవాబు :
8
![]()
ప్రశ్న102.
“A సమితి B సమితికి ఉపసమితి’ గుర్తును ఉపయోగించి రాయండి.
జవాబు :
A ⊂ B
ప్రశ్న103.
P = {x/x అనేది x2 – 16 యొక్క శూన్య విలువ, x ∈ Z విటున P సమితిని రాయండి.
జవాబు :
P = {4, -4} [∵ x2 – 16 = 0, x2 = 16
⇒ x = √16 = ± 4 4 మరియు – 4 ∈ Z]
ప్రశ్న104.
A = {1, 2, 3} అయిన Aకి గల ఉపసమితులు అన్నింటిని రాయండి.
జవాబు :
{ }, {1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}, {1, 2, 3}
ప్రశ్న105.
A ∪ B = {2, 3, 5, 8, 13, 21, 34}. A, B లు వియుక్త సమితులు మరియు A = {3, 13, 21, 34} అయిన B సమితిని కనుగొనుము.
జవాబు :
B = {2, 5, 8}
→ ఇవ్వబడిన వెన్ చిత్రాన్ని పరిశీలించి, క్రింది 106 – 111 వరకు గల ప్రశ్నలకు సమాధానాలు రాయండి.
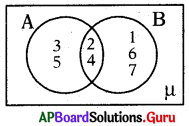
ప్రశ్న106.
A ∪ B =
జవాబు :
{1, 2, 3, 4, 5, 6, 7}
ప్రశ్న107.
A ∩ B =
జవాబు :
{2, 4}
ప్రశ్న108.
A – B =
జవాబు :
{3, 5}
ప్రశ్న109.
n(A) =
జవాబు :
4
ప్రశ్న110.
n[(A – B) ∪ (B – A)] =
జవాబు :
5
ప్రశ్న111.
n(A) + n(B) – n(A ∪ B) =
జవాబు :
2
[∵ A = {2, 3, 4, 51, (A – B) ∪ (B – A) = {1, 3, 5, 6, 7}
n(A) + n(B) – n(A ∪ B) = n(A ∩ B) = 2]
ప్రశ్న112.
A ∩ Φ = Φ ∩ A = ________
జవాబు :
Φ
![]()
ప్రశ్న113.
A ∩ μ = μ ∩ A = ________
జవాబు :
A
ప్రశ్న114.
క్రింది వెన్ చిత్రంలో A ∩ B = {6, 11} అయి x = 6 అయిన y విలువ ఎంత ?
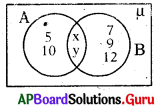
జవాబు :
11
ప్రశ్న115.
A ∪ A =
జవాబు :
A
ప్రశ్న116.
n(A) = 5, n(B) = 2 మరియు A, B లు వియుక్త సమితులు అయిన n(A ∪ B) విలువ ఎంత ?
జవాబు :
7
ప్రశ్న117.
A ∩ A =
జవాబు :
A
ప్రశ్న118.
A, B లు వియుక్త సమితులు అయిన n(A) + n(B) =
జవాబు :
n(A ∪ B)
ప్రశ్న119.
క్రింది వెన్ చిత్రంలో షేడ్ చేసిన ప్రాంతం సూచించు సమితిని రాయండి.
జవాబు :
A – B
ప్రశ్న120.
A = {2, 4, 8, 16} యొక్క నిర్మాణ రూపంను రాయండి.
జవాబు :
{x : x = 2n : n ∈ N, n < 5}
ప్రశ్న121.
క్రింది వెన్ చిత్రం నుండి B – A సమితిని రాయండి.
జవాబు :
{6, 9}
ప్రశ్న122.
(A – B) ∩ (B – A) = ________
జవాబు :
Φ
ప్రశ్న123.
క్రింది వెన్ చిత్రం నుండి B – A = ________

జవాబు :
B
ప్రశ్న124.
A={2} సమితి యొక్క ఉపసమితులు అన్ని రాయండి.
జవాబు :
2
ప్రశ్న125.
n(A ∪ B) = 14, n(A) = 8, n(A ∩ B) = 4 అయిన n(B) ని కనుగొనుము.
జవాబు :
n(A) + n(B) = n(A ∪ B) + n(A ∩ B)
8 + n(B) = 14 + 4 = 18
n(B) = 18 – 8 = 10
![]()
ప్రశ్న126.
సమితి నిర్మాణ రూపాన్ని, రోస్టర్ రూపానికి జతపరుచుము.
| a) {x : x సరి ప్రధానాంకము} | i) {0} |
| b) {x : X అనేది సున్నా కన్నా చిన్నదైన పూర్ణాంకము} | ii) {1} |
| c) {x.: x + 3 = 3, x ∈ W} | iii) {2} |
| D) {x : x2 = 1, x ∈ N} | iv) Φ |
A) a-iii, b-iv, c-i, d-ii
B) a-iii, b-ii, c-i, d-iv
C) a-iii, b-i, c-iv, d-ii
D) a-i, b-iv, c-ii, d-iii
జవాబు :
A) a-iii, b-iv, c-i, d-ii
ప్రశ్న127.
A = చతుర్భుజాల సమితి, B = చతురస్రాల సమితి, C = రాంబస్ సమితి అయిన క్రింది వానిలో ఏవి అసత్యం ?
i) B ⊂ C
ii) B ⊂ C ⊂ A
iii) A ⊂ B
iv) C ⊂ B
A) i, ii
B) iii, iv
C) i, iv
D) ii, iii
జవాబు :
B) iii, iv
ప్రశ్న128.
ప్రవచనం-P : A ⊂ B, B ⊂ A అయిన A = B
ప్రవచనం-Q : n(A) = n(B) అయిన A = B
A) P సత్యం, Q అసత్యం
B) P అసత్యం, Q సత్యం
C) P Q లు రెండూ సత్యం
D) P, Q లు రెండూ అసత్యం
జవాబు :
A) P సత్యం, .Q అసత్యం
ప్రశ్న129.
పరిమిత సమితికి ఒక ఉదాహరణనివ్వండి.
జవాబు :
{5, 7, 9}
ప్రశ్న130.
A ⊂ B అయిన n(A ∪ B) = ________
A) n(A)
B) n(B)
C) n(A ∩ B)
D) 0
జవాబు :
B) n(B)
ప్రశ్న131.
ACB అయిన n(A ∩ B) = ________
A) n(A)
B) n(B)
C) n(A ∪ B)
D) 0
జవాబు :
A) n(A)
ప్రశ్న132.
A ⊂ B = A – B = ________
A) A
B) B
C) Φ
D) µ
జవాబు :
C) Φ
ప్రశ్న133.
A = {x: x అనేది a= 2,d = 3 గా గల అంకశ్రేఢిలోని పదం మరియు x < 12} అయిన A యొక్క రోస్టర్ రూపాన్ని రాయండి.
జవాబు :
A = {2, 5, 8, 11}
ప్రశ్న134.
A అనేది x + 2 = 0 యొక్క సాధన సమితి, B అనేది x2 – 4 = 0 యొక్క సాధన సమితి అయిన A ∩ B =
జవాబు :
A = {-2}, B = {2, – 2}
∴ A ∩ B = {-2} , [∵ x + 2 = 0 ⇒ x = -2
x2 – 4 = 0 ⇒ x2 = 4
⇒ x = √4 = ± 2]
ప్రశ్న135.

వెన్ చిత్రంలో షేర్ చేసిన ప్రాంతాన్ని సూచించు సమితిని రాయండి.
జవాబు :
B – A
ప్రశ్న136.
అపరిమిత సమితికి ఒక ఉదాహరణనివ్వండి.
జవాబు :
{1, 2, 3, 4, 5, 6, …………… }
ప్రశ్న137.
B – A ను వెన్ చిత్రంలో చూపండి.
జవాబు :
ప్రశ్న138.
n(P) = 4 అయ్యే విధంగా సమితి P కి ఒక ఉదాహరణనివ్వండి.
జవాబు :
P = {0, 1, 2, 3}, n(P) = 4.
→ క్రింది వెన్ చిత్రాన్ని పరిశీలించి 139 మరియు 140 ప్రశ్నలకు సమాధానాలు రాయండి.
ప్రశ్న139.
విశ్వసమితి μని రాయండి.
జవాబు :
μ = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
ప్రశ్న140.
(A – B) ∪ (B – A) సమితిని రాయండి.
జవాబు :
(A – B) ∪ (B – A) = {3, 4, 5, 6, 7, 8, 10}
ప్రశ్న141.
అకరణీయ సంఖ్యా సమితి మరియు వాస్తవ సంఖ్యా సమితులు యొక్క ఛేదనము (intersection) …….. సమితి అగును.
A) వాస్తవ సంఖ్య
B) అకరణీయ సంఖ్య
C) పూర్ణ సంఖ్య
D) కరణీయ సంఖ్య
జవాబు :
B (∵ అకరణీయ సంఖ్యా సమితి Q ⊂ వాస్తవ సంఖ్యా సమితి R
∴ Q ∩ R = Q)
![]()
ప్రశ్న142.
“A, B లు వియుక్త సమితులు”, ఈ సమాచారాన్ని సూచించుటకు సరైన వెన్ చిత్రము ఏది ?
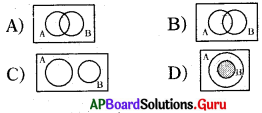
జవాబు :
C
ప్రశ్న143.
జతపరచండి :
| i) {log101, log10 10} | a) {3, 5) |
| ii) {x/x అనేది 36 యొక్క ప్రధాన కారణాంకము} | b) {-3, 3} |
| iii){x/x = 2n + 1, n ∈ N మరియు n <3} | c) {0, 1}; |
| iv) {x/x అనేది x2 – 1 = 8 యొక్క సాధన} | d) {2, 3} |
A) i – c, ii – d, iii – a, iv – b
B) i – c, ii – a, iii – b, iv – d
C) i – c, ii – d, iii – b, iv – a
D) i – d, ii – a, iii – c, iv – b
జవాబు :
A) i – c, ii – d, iii – a, iv – b
ప్రశ్న144.
i) A = B అయిన n(A) = n(B)
ii) n(A) = n(B) అయిన A = B అయిన
A) i మాత్రమే సత్యం
B) ii మాత్రమే సత్యం
C) i మరియు ii లు సత్యం
D) పైవి ఏవీ కావు
జవాబు :
A) i మాత్రమే సత్యం
ప్రశ్న145.
A = {x/x అనేది 45 యొక్క ప్రధాన కారణాంకం},
B = {log28, log216} అయిన A ∪ B =
A) {4, 5}
B) {3, 5}
C) {3, 4}
D) {3, 4, 5}
జవాబు :
D) {3, 4, 5}
A = {3, 5}, B = {3, 4}
∴ A ∪ B = {3, 4, 5}
[∵ 45 = 32 × 5
log2 8 = log2 23 = 3 log22 = 3
log2 16 = log224 = 4 log22 = 4]
ప్రశ్న146.
A = {1, 2, 5, 6}; A – B = {1, 2} అయిన క్రింది వానిలో సత్యమేది ?
A) 5 ∈ B
B) 6 ∈ B
C) n(B) ≥ 2
D) పైవన్నీ
జవాబు :
D) పైవన్నీ
ప్రశ్న147.
n(A) = 8, n(B) = 6, A, B లు వియుక్త సమితులు కానిచో n(AUB) = ….
A) 14
B) ≥ 8
C) <14
D) B మరియు C
జవాబు :
D) B మరియు C
ప్రశ్న148.
A = {x:x అనేది 30 యొక్క ప్రధాన కారణాంకము} ‘
B= {x:x అనేది 7 కన్నా చిన్నదైన ప్రధాన సంఖ్య} అయిన A = B అని చూపుము.
జవాబు :
A = {2, 3, 5} [∵ 30 = 2 × 3 × 5
B = {2, 3, 5} {∵ 7 కన్నా చిన్నవైన ప్రధాన సంఖ్యలు 2, 3, 5}
∴ A = B
ప్రశ్న149.
క్రింది సమితి Aని ఉద్దేశించి ఈ క్రింది నీయబడిన ప్రవచనాల statements నుండి సరైన జవాబు గుర్తించండి. A = {1, 2, 3, 4}
i) n(A) = 4
ii) సమితి ‘A’ కి గల ఉపసమితుల సంఖ్య 16
A) i సత్యం, ii అసత్యం
B) i అసత్యం , ii సత్యం
C) i మరియు ii లు రెండూ సత్యం
D) i మరియు ii లు రెండూ అసత్యం
జవాబు :
C) i మరియు ii లు రెండూ సత్యం
ప్రశ్న150.
P= {x: x అనునది – 4, 4 ల మధ్య గల సహజ సంఖ్య} అయిన
A) n(P) = 7
B) n(P) = 9
C) n(P) = 3
D) n(P) = 16
జవాబు :
C) n(P) = 3
ప్రశ్న151.
A = {2,3,5} యొక్క నిర్మాణ రూపం –
A) {x/X అనునది మొదటి 6 కన్నా తక్కువైన ప్రధాన సంఖ్య
B) {x/X అనునది 20 యొక్క కారణాంకం}
C) {x/X అనునది 30 యొక్క ప్రధాన కారణాంకము
D) A మరియు C
జవాబు :
D) A మరియు C
ప్రశ్న152.
X = {2, 5} అయిన ఈ క్రింది వానిలో ఏది సత్యం ?
A) X ⊂ X
B) 2 ∈ X
C) Φ ⊂ X
D) పైవన్నీ
జవాబు :
D) పైవన్నీ
ప్రశ్న153.
n(P ∪ Q) = 36, n(P) = 23, n(Q) – 25 అయిన n(P ∩ Q) విలువ ఎంత ?
జవాబు :
n(P) + n(Q) = n(P ∪Q) + n(P ∩ Q)
23 + 25 = 36 + n(P ∩ Q)
48 – 36 = n(P ∩ Q)
n(P ∩ Q) = 12
ప్రశ్న154.
Y = {x/x అనునది [latex]\frac{-7}{2}[/latex] మరియు [latex]\frac{-15}{2}[/latex] ల మధ్య గల పూర్ణ సంఖ్య} అయిన n(Y) విలువ ఎంత ?
జవాబు :
Y = {-4, – 5, – 6, – 7}, n(Y) = 4 .
[latex]\frac{-7}{2}[/latex] = – 3.5, [latex]\frac{-15}{2}[/latex] = -7.5
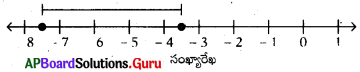
ప్రశ్న155.
A = {log101}, B = {log1010, log102} అయిన n(A ∩ B) =
A) n(Φ)
B) 0
C) A మరియు B
D) n(A ∪ D)
జవాబు :
B) 0
[∵ A ∩ B = Φ, n(A ∩ B) = n(Φ) = 0]
![]()
ప్రశ్న156.
జతపరచుము :
| గ్రూపు A | గ్రూపు B |
| P) Φ ∪ A | i) AUB |
| Q) μ ∪ Α | ii) AnB |
| R) (A ∪ D) n (A ∩ B) | iii) 4 |
| iv) A | |
| v) μ |
A) P (iv), Q (v), R (i)
B) P (iv), Q (v), R (ii)
C) P (iv), Q (ii), R (iii)
D) పైవేవీకావు
జవాబు :
B
ప్రశ్న157.
ఈ క్రింది వానిలో శూన్య సమితులేవి ”
A) రెండు ఖండన రేఖలకు గల ఉమ్మడి బిందువుల సమితి
B) వృత్త కేంద్రంనకు సమాన దూరంలోగల రెండు వేర్వేరు జ్యాల ఖండన బిందువుల సమితి
C) 8 మంది కంటే చిన్నది మరియు 9 కంటే పెద్దదైన సహజ సంఖ్యల సమితి
D) ‘B’ మరియు ‘C’
జవాబు :
D) ‘B’ మరియు ‘C’
ప్రశ్న158.
క్రింది వానిలో శూన్యసమితులను వేరుచేసి రాయండి.
A = {x : x < 1, x ∈ N}
B = {x : x + 1 = 3, x ∈ N}
C = {x : x2 = 4, x ∈ Z}
D = 2, 3 ల మధ్యగల పూర్ణాంకాల సహిత
E= {0, 1,3}
జవాబు :
శూన్యసమితులు = A, C, D
ప్రశ్న159.
P = {x/x2 = – 4 అయ్యేట్లు ఒక సహజ సంఖ్య } అయిన
A) P ఒక పరిమిత సమితి
B) P ఒక వాన్య సమితి
C) పై రెండూ
D) పైవేవీ కావు
జవాబు :
C) పై రెండూ
ప్రశ్న160.
A అనునది. తొలి పదం’ 0 గాను, పదాంతరం 2 గా గల్గిన అంకశ్రేణిలోని తొలి 5 పదాలు కలిగిన సమితి;
B అనునది తొలిపదం 8 గాను, పదాంతరం – 2 గా గల్గిన అంకశ్రేణిలోని తొలి 5 పదాలు కలిగిన సమితి అయిన .
i) n(A) = n(B),
ii) A = B
A) (i) మరియు (ii) లు రెండూ అసత్యం
B) (i) సత్యం (ii) అసత్యం
C) (i) అసత్యం , (ii) సత్యం
D) (i) మరియు (ii) రెండూ సత్యం
జవాబు :
D) (i) మరియు (ii) రెండూ సత్యం
A = {0, 2, 4, 6, 8}; B = {8, 6, 4, 2, 0}
A = B, n(A) = n(B) = 5
ప్రశ్న161.
A పరిమిత సమితి, B అపరిమిత సమితి అయిన
A) n(A ∩ B) = 0 కావచ్చును
B) (A ∪ B) ఒక అపరిమిత సమితి కావచ్చును
C) (A ∩ B) ఒక పరిమిత సమితి కావచ్చును
D) పైవన్నీ కావచ్చును
జవాబు :
D) పైవన్నీ కావచ్చును
ప్రశ్న162.
i) శూన్య సమితి గుర్తు Φ
ii) Φ నందలి మూలకాల సంఖ్య 0 కావున Φ ఒక పరిమిత సమితి
A) (i) మాత్రమే సత్యం
B) (i) మరియు (ii) లు రెండూ సత్యం
C) (ii) మాత్రమే సత్యం
D) (i) మరియు (ii) లు రెండూ అసత్యం
జవాబు :
B) (i) మరియు (ii) లు రెండూ సత్యం
ప్రశ్న163.
i) శూన్య సమితి ఒక పరిమిత సమితి
ii) విశ్వ సమితి ఒక అపరిమిత సమితి కావచ్చును
iii) విశ్వసమితి ఎల్లపుడూ ఒక పరిమిత సమితి అగును
A) i → T, ii → T, iii → F
B) i → T , ii → F, iii → i.
C) i → T, ii → T, iii → T
D) i → F, ii → F, iii → F
జవాబు :
A) i → T, ii → T, iii → F
ప్రశ్న164.
A = {x/x అనునది x2 – 5x + 6 యొక్క శూన్యం } అయిన A సమితిని రోస్టర్ రూపంలో రాయండి.
జవాబు :
x2 – 5x + 6 = 0
⇒ x2 – 2x – 3x + 6 = 0
⇒ x (x – 2) – 3 (x – 2) = 0
(x – 2) (x – 3) = 0
శూన్యాలు 2, 3
∴ A = {2, 3}
ప్రశ్న165.
P అనునది TEACHER అనే పదంలోని అక్షరం మూలకంగా గల సమితి అయిన n(P) విలువను కనుగొనుము.
జవాబు :
P = {T, E, A, C, H, R}
n(P) = 6
ప్రశ్న166.
P = {1, 2, 3, 4}; P ∪ Q = {1, 2, 3, 4, 5, 6} అయిన n(Q) కనిష్ఠ, గరిష్ట విలువలు రాయండి.
జవాబు :
n(Q) కనిష్ఠ విలువ 2, గరిష్ఠ విలువ = 6
(∵n(Q) విలువ P,Q లు వియుక్త సమితులైనప్పుడు కనిష్ఠంగాను, P ⊂ Q అయిన P ∪ Q = Q అయినపుడు గరిష్ఠంగాను ఉంటుంది).
ప్రశ్న167.
A, B లు సమసమితులు అవుతాయా ? కాదా ? ఎందుకు ?
జవాబు :
A = {R, O, P, E}, B = {P, 0, R, E}
A, B లు ఒకే మూలకాలను కలిగి ఉన్నాయి.
∴ A = B
ప్రశ్న168.
A = {p, q, r}; B = {q, r, s}
A మరియు B లు వియుక్త సమితులు (సత్యం / అసత్యం ).
జవాబు :
అసత్యం
ప్రశ్న169.
n(P) = 8; n(Q) = 6, P – Q; అయిన
n(P ∪ Q) + n(P ∩ Q) విలువను గణించండి. సాధన. n(P ∪ Q) + (P ∩ Q)
= n(P) + n(Q) = 8 + 6 = 14
ప్రశ్న170.
n(P) + n(Q) = n(P ∪ Q) అయిన ‘P’, ‘Q’ లను గూర్చి నీవు ఏమి చెప్పగలవు ?
జవాబు :
P ∩ Q = Q (లేదా) P, Q లు వియుక్త సమితులు.
ప్రశ్న171.
X, Y సమితులు వియుక్త సమితులు కాకుండునట్లు X,Y లకు ఒక ఉదాహరణను ఇవ్వండి.
జవాబు :
X = {3, 5, 7,, Y = {2, 3, 4, 5}
ప్రశ్న172.
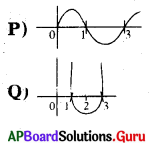
P అనునది బహుపదిలోని శూన్యాల సమితి;
Q అనునది వర్గబహుపది శూన్యాల సమితి అయిన
P – Q సమితిని కనుగొనుము.
జవాబు :
P = {0, 1, 3}, Q = {1, 3}
P – Q = {0, 1, 3} – {1, 3} = {0}
ప్రశ్న173.
n(T) = 20; n(C) = 30; n(T ∩ C) = 10 అయిన n(T – C) = ________
A) 10
B) – 10
C) 20
D) 30
జవాబు :
A) 10
n(T – C) = n(T) = n(T ∩ C)
= 20 – 10 = 10
ప్రశ్న174.
A ⊂ B, n(A) = 15 మరియు n(B) = 20 అయిన n(A – B) విలువ ఎంత ?
జవాబు :
A ⊂ B అయిన A – B = Φ
∴ n(A – B) = “0”
![]()
ప్రశ్న175.
A = {tan 45, sec 30, cos 60},
B = {cot 45, cosec x, sin 30} మరియు A = B అయిన X =
A) 30°
B) 60°
C) 90°
D) నిర్ణయించలేము
జవాబు :
B) 60°
A = {tan 45°, sec 30°, cos 60°}
= {1, [latex]\frac{2}{\sqrt{3}}, \frac{1}{2}[/latex]}
B = {cot 45°, cosec x, sin 30°}
= {1, cosec X, [latex]\frac{1}{2}[/latex]}
A = B కావున cosec X = [latex]\frac{2}{\sqrt{3}}[/latex]
X = 60°
(లేదా)
A, B లలో వరుసగా tan 45° = cot 45°
cos 60° = sin 30° కావున
cosec X = sec 30° = [latex]\frac{2}{\sqrt{3}}[/latex] కావలెను
X = 60°
[∵ cosec 60° = [latex]\frac{2}{\sqrt{3}}[/latex]]
ప్రశ్న176.
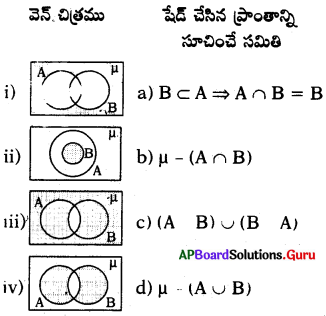
క్రింది సమితుల రోస్టర్ రూపాన్ని, వాని యొక్క సమితి నిర్మాణ రూపానికి జతపరచుము :

A) i – b, ii – c, iii – d, iv – a
B) i – c, ii – b, iii – a, iv – d
C) i – c, ii – d, iii – a, iv – b
D) i – b, ii – d, iii – a, iv – c
జవాబు :
C) i – c, ii – d, iii – a, iv – b
ప్రశ్న177.
A) i – b, ii – a iii – d, iv – c
B) i – c, ii – a, iii – d, iv – b
C) i – d, ii – a, iii – b, iv – c
D) i – d, ii – c, iii – b, iv – a
జవాబు :
C) i – d, ii – a, iii – b, iv – c
→ A = {x: x అనే – (x – 3) (x + 5) యొక్క శూన్యము}
శూన్యము B = {x: x అనేది (x – 3) (x – 5) (x – 6) యొక్క శూన్యము} అయితే
క్రింది 178-180 వరకు గల ప్రశ్నలకు సమాధానాలు రాయండి.
ప్రశ్న178.
A ∪ Bని కనుగొనుము.
జవాబు :
A = {3, – 5}, B = {3, 5, 6}
A ∪ B = {-5, 3, 5, 6}
ప్రశ్న179.
A ∩ Bని కనుగొనుము.
జవాబు :
A = {3, – 5}, B = {3, 5, 6} .
A ∩ B = {3}
ప్రశ్న180.
(A ∪ D) – (A ∩ B) సమితిని రాయండి.
జవాబు :
(A ∪ D) – (A ∩ B) = {-5, 3, 5, 6} – {3}
= {-5, 5, 6}
ప్రశ్న181.
A = {1, 2, 3} మరియు Φ = { } అయిన A ∩ Φ కనుగొనండి.
జవాబు :
Φ
ప్రశ్న182.
క్రింది వెన్ చిత్రాన్ని పరిశీలించి, n(A ∪ B) విలువ కనుగొనండి.
జవాబు :
5
ప్రశ్న183.
మూడు విభిన్న మూలకాలను కలిగిన సమితి ఎని ఉపసమితులను కలిగి ఉంటుంది ?
జవాబు :
8 ఉపసమితులు.
ప్రశ్న184.
A = {1, 2, 3} మరియు B = {2, 4, 6} అయిన n(A ∪ D) ఎంత ?
జవాబు :
A = {1, 2, 3}, B = {2, 4, 6}
A ∪ B = {1, 2, 3} ∪ {2, 4, 6}
= {1, 2, 3, 4, 6}
n(A ∪ B) = 5