AP 10th Class Maths Bits 1st Lesson వాస్తవ సంఖ్యలు

Practice the AP 10th Class Maths Bits with Answers 1st Lesson వాస్తవ సంఖ్యలు on a regular basis so that you can attempt exams with utmost confidence.

AP Board 10th Class Maths Bits 1st Lesson వాస్తవ సంఖ్యలు

ప్రశ్న 1.
log_a\(\frac{\mathbf{x}}{\mathbf{y}}\)
(A) \(\frac{\log _{a} x}{\log _{a} y}\)
(B) log_ax – log_ay
(C) log_ax + log_ay
(D) log_ax – y.
జవాబు.
(B) log_ax – log_ay

ప్రశ్న 2.
0.0875 యొక్క \(\frac{\mathbf{p}}{\mathbf{q}}\) రూపంను రాయండి.
సాధన.
0.0875 = \(\frac{875}{10000}\) = \(\frac{875}{2^{4} \times 5^{4}}\) = \(\frac{7}{2^{4} \times 5}\)

ప్రశ్న 3.
p ప్రధాన సంఖ్య అయిన √P
(A) సంయుక్త సంఖ్య
(B) అకరణీయ సంఖ్య
(C) ధనపూర్ణ సంఖ్య
(D) కరణీయ సంఖ్య
జవాబు
(D) కరణీయ సంఖ్య

ప్రశ్న 4.
\(\frac{52}{160}\) = \(\frac{13}{2^{n} \times 5^{m}}\) అయిన m + n విలువను కనుగొనుము.
సాధన.
\(\frac{52}{160}\) = \(\frac{2^{2} \times 13}{2^{5} \times 5}\) = \(\frac{13}{2^{3} \times 5}\) = \(\frac{13}{2^{n} \times 5^{m}}\)
n = 3, m = 1
∴ m + n = 3 + 1 = 4

ప్రశ్న 5.
log 625 = k log 5 అయిన ఓ విలువ ఎంత ?
సాధన.
log 625 = k log 5
log 5⁴ = k log 5
4 log 5 = k log 5
∴ k = 4

ప్రశ్న 6.
log₂ x = 3 అయిన X విలువ ఎంత ?
సాధన.
log₂x = 3 ను ఘాతరూపంలో రాయగా
2³ = x
∴ x = 8

ప్రశ్న 7.
\(\frac{1}{2}\) మరియు √1 ల మధ్య గల అకరణీయ సంఖ్య ………………..
(A) \(\frac{9}{4}\)
(B) \(\frac{3}{4}\)
(C) \(\frac{5}{4}\)
(D) \(\frac{7}{4}\)
సాధన.
(B) \(\frac{3}{4}\)

వివరణ:
\(\frac{1}{2}\) మరియు √1 ల మధ్య గల అకరణీయ సంఖ్య
= \(\frac{\frac{1}{2}+1}{2}\) = \(\frac{\frac{3}{2}}{2}\) = \(\frac{3}{4}\)

ప్రశ్న 8.
కరణీయ, అకరణీయ సంఖ్యల సమ్మేళన సమితి ఏది?
జవాబు.
వాస్తవ సంఖ్యల సమితి (R).

ప్రశ్న 9.
3⁵ = 243 యొక్క సంవర్గమాన రూపం రాయండి.
సాధన.
log₃ 243 = 5

ప్రశ్న 10.
“అయినచో” అనే సంయోజకమునకు గుర్తును రాయండి.
జవాబు.
⇒

ప్రశ్న11.
729 యొక్క ప్రధాన కారణాంకంను రాయండి.
సాధన.
729 = 3⁶

ప్రశ్న 12.
X మరియు y లు రెండు ప్రధాన సంఖ్యలైతే వాటి గసాభా ఎంత ?
జవాబు.
1

ప్రశ్న 13.
log₁₀0.01 విలువ ఎంత ?
సాధన.
log₁₀0.01 = log₁₀10^-2
= – 2 log₁₀10 = – 2 (1) = – 2

ప్రశ్న 14.
0 నుండి 100 వరకు గల బేసి సంఖ్యల సంఖ్య ఎంత ?
జవాబు.
50

ప్రశ్న 15.
log₄ 8 = x యొక్క ఘాత రూపంను రాయండి.
సాధన.
4^x = 8

ప్రశ్న 16.
\(\frac{36}{2^{3} \times 5^{3}}\) విలువను దశాంశ రూపంలో తెల్పండి. ”
సాధన.
\(\frac{36}{2^{3} \times 5^{3}}\) = \(\frac{36}{(2 \times 5)^{3}}\) = \(\frac{36}{1000}\) = 0.03

ప్రశ్న 17.
రెండు సంఖ్యల కసాగు 108 మరియు గసాకా 9 అయిన అందులో ఒక సంఖ్య 54 అయిన రెండవ సంఖ్య ఎంత?
సాధన.
క.సా.గు × గ.సా.భా = రెండు సంఖ్యల లబ్దం
108 × 9 = 54 × x
∴ x = \(\frac{108 \times 9}{54}\) = 18

ప్రశ్న 18.
36 కు గల ప్రధాన కారణాంకాల సంఖ్య ఎంత ?
సాధన.
36 = 2² × 3², కావున 36 యొక్క ప్రధాన కారణాంకాలు 2, 3.
∴ 36 యొక్క ప్రధాన కారణాంకాల సంఖ్య = 2

ప్రశ్న 19.
log₁₀0.001 = – 3 యొక్క ఘాతాంక రూపంను రాయండి.
సాధన.
10^-3 = 0.001

ప్రశ్న 20.
ఈ క్రింది వానిలో అకరణీయ సంఖ్య కానిది ……
(A) log₁₀3
(B) 5.\(\overline{23}\)
(C) 123.123
(D) \(\frac{10}{19}\)
జవాబు.
(A) log₁₀3

ప్రశ్న 21.
24, 36 ల క.సా.గు ను తెల్పండి.
సాధన.
24 = 2³ × 3, 36 = 2² × 3²,
24, 36 ల క.సా.గు = 2³ × 3² = 72

ప్రశ్న 22.
log₇1 విలువ ఎంత ?
జవాబు.
0

ప్రశ్న 23.
a^b = c యొక్క సంవర్గమాన రూపం
(A) log^a c = b
(B) log^b c = a
(C) log^a b = c
(D) log^b a = c
జవాబు.
(A) log^a c = b

ప్రశ్న 24.
3 log (x + 3) = log 27 అయిన x విలువ ఎంత?
సాధన.
3 log (x + 3) = log 27
log (x + 3)³ = log 27
∴ (x + 3)³ = 27
⇒ (x + 3)³ = 33
⇒ x + 3 = 3
⇒ x = 3 – 3 = 0
∴ x = 0

ప్రశ్న 25.
ఈ క్రింది అకరణీయ సంఖ్యలలో దేనికి అంతమయ్యే దశాంశ రూపం ఉంటుంది?
(A) \(\frac{11}{7000}\)
(B) \(\frac{91}{21000}\)
(C) \(\frac{343}{2^{3} \times 5^{3} \times 7^{3}}\)
(D) \(\frac{21}{9000}\)
జవాబు.
(C) \(\frac{343}{2^{3} \times 5^{3} \times 7^{3}}\)

ప్రశ్న 26.
log₂₅ 5 = \(\frac{1}{2}\) అని చూపుము.
సాధన.
log₂₅ 5 = x
∴ 25^x = 5 = √25
⇒ 25^x = 25^1/2
⇒ x = \(\frac{1}{2}\)
∴ log₂₅5 = \(\frac{1}{2}\)

ప్రశ్న 27.
2.\(\overline{6}\) కు సమానమైన అకరణీయ సంఖ్య
(A) \(\frac{7}{3}\)
(B) \(\frac{8}{3}\)
(C) \(\frac{16}{3}\)
(D) \(\frac{17}{7}\)
జవాబు.
(B) \(\frac{8}{3}\)

ప్రశ్న 28.
అంకగణిత థమిక సిద్ధాంతం క్రింది వానిలో దేనికి అనువర్తిస్తుంది ?
(A) 4
(B) 3
(C) 2
(D) 1
జవాబు.
(B) 3

ప్రశ్న 29.
6⁵⁰ విస్తరణలో చివరి అంకె ఏది ?
జవాబు.
6

ప్రశ్న 30.
ఈ క్రింది వానిలో అంతమయ్యే దశాంశం ఏది?
(A) \(\frac{10}{81}\)
(B) \(\frac{41}{75}\)
(C) \(\frac{8}{125}\)
(D) \(\frac{3}{14}\)
జవాబు.
(C) \(\frac{8}{125}\)

ప్రశ్న 31.
log₂ 32 విలువ ఎంత ?
సాధన.
log₂ 32 = log₂ 2⁵ = 5 log₂ 2 = 5(1) = 5

ప్రశ్న 32.
క్రింది వానిలో కరణీయ సంఖ్య కానిది ఏది ?
(A) √2
(B) √3
(C) √4
(D) √5
జవాబు.
(C) √4

ప్రశ్న 33.
6²⁰²⁰ + 5²⁰²¹ లో ఒకట్ల స్థానంలోని సంఖ్య
(A) 6
(B) 5
(C) 1
(D) 0
జవాబు.
(C) 1

ప్రశ్న 34.
log_a \(\sqrt{x^{4}}\) = y యొక్క ఘాతరూపం –
(A) a^y = x⁴
(B) y^a = 4
(C) a^y = x²
(D) x^y = a²
జవాబు.
(C) a^y = x²

ప్రశ్న 35.
6²⁰¹⁹ యొక్క విస్తరణ రూపంలోని ఒకట్ల స్థానంలో ఉండే అంకె ఏది ?
జవాబు.
6

ప్రశ్న 36.
క్రింది వానిలో కరణీయ సంఖ్య ఏది ?
(A) √4
(B) √3
(C) \(\frac{5}{2}\)
(D) \(\frac{2}{3}\)
జవాబు.
(B) √3

ప్రశ్న 37.
క్రింది వానిలో అకరణీయ సంఖ్య ఏది ?
(i) 2 – √3
(ii) √4 – √25
(A) (i) మాత్రమే
(B) (ii) మాత్రమే
(C) (i) మరియు (ii)
(D) (i) మరియు (ii)లు కావు
జవాబు.
(B) (ii) మాత్రమే

ప్రశ్న 38.
√2 మరియు √3 ల మధ్యగల అకరణీయ సంఖ్య
(A) \(\frac{3}{2}\)
(B) \(\frac{5}{2}\)
(C) \(\frac{1}{2}\)
(D) 1
జవాబు.
(A) \(\frac{3}{2}\)

ప్రశ్న 39.
క్రింది వానిలో \(\frac{1}{2}\) మరియు 1ల మధ్య లేనటువంటి ఒక అకరణీయ సంఖ్యను రాయండి.
జవాబు.
1.5

ప్రశ్న 40.
m ధన పూర్ణ సంఖ్య అయిన \(\sqrt{2 \mathrm{~m}+1}\) అకరణీయ సంఖ్య కావడానికి m యొక్క కనిష్ఠ విలువ ఎంత ?
సాధన.
m ధనపూర్ణ సంఖ్య మరియు \(\sqrt{2 \mathrm{~m}+1}\) అకరణీయ సంఖ్య అయిన 2m + 1 ఖచ్చిత వర్గం కావలెను.
∴ 2m + 1 = 1 లేదా 4 లేదా 9 …. కావలెను.
2m + 1 = 1 ⇒ m = 0
2m + 1 = 4 ⇒ m = \(\frac{3}{2}\)
2m + 1 = 9 ⇒ m = 4
0, \(\frac{3}{2}\)లు ధనపూర్ణ సంఖ్యలు కావు. కావున m యొక్క కనిష్ఠ విలువ = 4

ప్రశ్న 41.
x, yలు ప్రధానాంకాలు అయిన x³y² మరియు x²y³ల గ.సా.భాను రాయండి.
జవాబు.
x²y²

ప్రశ్న 42.
క్రింది వానిలో కరణీయ సంఖ్య ఏది ? –
(A) (2 + √3) + (2 – √3)
(B) (2 + √3) (2 – √3)
(C) √2 + √8
(D) √2.√8
జవాబు.
(C) √2 + √8

ప్రశ్న 43.
క్రింది వానిలో 5005 యొక్క ప్రధాన కారణాంకం కానిది.
(A) 11
(B) 7
(C) 5
(D) 3
జవాబు.
(D) 3

ప్రశ్న 44.
3825 యొక్క ప్రధాన కారణాంకాల లబ్ధంను రాయండి.
సాధన.
3825 = 3² × 5² × 17

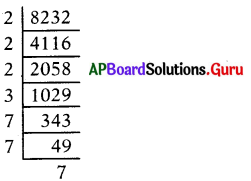
ప్రశ్న 45.
8232 = 2³ × 3 × 7ⁿ అయిన n విలువ ఎంత ?
సాధన.
8232 = 2³ × 3 × 7ⁿ
2³ × 3 × 7³ = 2³ × 3 × 7ⁿ
∴ n = 3

ప్రశ్న 46.
156 = 2² × 3 × k అయిన k విలువ ఎంత ?
సాధన.
156 = 2² × 3 × k
2² × 3 × 13 = 2² × 3 × k
∴ k = 13

ప్రశ్న 47.
2³ × 3² × 5 మరియు 2² × 3³ × 5² యొక్క గ.సా.కా
(A) 2³ × 3³ × 5²
(B) 2² × 3² × 5
(C) 2³ × 3² × 5
(D) 2 × 3 × 5
జవాబు.
(B) 2² × 3² × 5

ప్రశ్న 48.
120, 150 మరియు 210లగ.సా.5 k² – 6 అయిన k విలువ ఎంత?
సాధన.
120 = 2³ × 3 × 5
150 = 2 × 3 × 5²
210 = 2 × 3 × 5 × 7
గ.సా.కా = 2 × 3 × 5 = 30
∴ k² – 6 = 30
⇒ k² = 36
⇒ k = √36
⇒ k = ± 6

ప్రశ్న 49.
అంకగణిత ప్రాథమిక సిద్ధాంతమును రాయండి.
జవాబు.
అంకగణిత ప్రాథమిక సిద్ధాంతము: ప్రతి సంయుక్త సంఖ్యను ప్రధాన కారణాంకాల లబ్దంగా రాయవచ్చును మరియు ప్రధాన కారణాంకాల క్రమం ఏదైనప్పటికి ఈ కారణాంకాల లబ్దము ఏకైకము.

ప్రశ్న 50.
29 మరియు 3 లకు యూక్లిడ్ భాగహార నియమం a = bq + rను అనువర్తింపజేస్తే q విలువ ఎంత ?
సాధన.
29 = 3 × 9 + 2
a = bq + r
∴ q = 9

ప్రశ్న 51.
2³ × 3 × 5 మరియు 2² × 5 × 7 యొక్క క.సా.గు ఎంత ?
సాధన.
క.సా.గు = 2³ × 3 × 5 × 7 = 840

ప్రశ్న 52.
a, b లు ధనపూర్ణ సంఖ్యలు అయిన a = bq + r అయ్యేటట్లు q, r అనే పూర్ణాంకాలు వ్యవస్థితం అనే యూక్లిడ్ భాగహార నియమంలో r విలువ ఎల్లప్పుడూ
(A) 0 ≤ r ≤ b
(B) 0 ≤ r ≤ b
(C) 1 < r < b
(D) 0 ≤ r < a
జవాబు.
(D) 0 ≤ r < a

ప్రశ్న 53.
రెండు సంఖ్యల లబ్దం 1600 మరియు వాని గ.సా.కా 5 అయిన ఆ సంఖ్యల క.సా.గు ఎంత ?
సాధన.
రెండు సంఖ్యల లబ్దం = క.సా.గు × గ.సా.భా
1600 = క.సా.గు × 5
∴ క.సా.గు = \(\frac{1600}{5}\) = 320

ప్రశ్న 54.
యూక్లిడ్ భాగహార నియమాన్ని రాయండి.
జవాబు.
యూక్లిడ్ భాగహార నియమం: a = bq + r,
0 ≤ r < b అయ్యే విధంగా a మరియు bల జతకు అనుగుణంగా q మరియు rలు ఏకైక ‘పూర్ణసంఖ్యలు వ్యవస్థితం అవుతాయి.

ప్రశ్న 55.
క్రింది వానిలో పరస్పర ప్రధానాంకాల జత
(A) (21, 49)
(B) (11, 55)
(C) (18, 25)
(D) (23, 69)
జవాబు.
(C) (18, 25)

ప్రశ్న 56.
23.34ను సూచించే అకరణీయ సంఖ్యను కనిష్ఠ రూపంలో రాయండి.
సాధన.
23.34 = \(\frac{2334}{100}\) = \(\frac{2334}{2^{2} \times 5^{2}}\) = \(\frac{1167}{2 \times 5^{2}}\)

ప్రశ్న 57.
కింది వానిలో అంతం కాని ఆవర్తనం అయ్యే దశాంశము ఏది ?
(A) \(\frac{105}{48}\)
(B) \(\frac{41}{75}\)
(C) \(\frac{25}{32}\)
(D) \(\frac{16}{125}\)
జవాబు.
(B) \(\frac{41}{75}\)

ప్రశ్న 58.
కింది వానిలో అంతమయ్యే దశాంశము ఏది ?
(A) \(\frac{11}{12}\)
(B) \(\frac{143}{110}\)
(C) \(\frac{41}{75}\)
(D) \(\frac{100}{81}\)
జవాబు.
(B) \(\frac{143}{110}\)

ప్రశ్న 59.
a = bq + r (a, bలు ధన పూర్ణసంఖ్యలు) యూక్లిడ్ భాగహార న్యాయంలో r = 0 అయిన
(A) as b కారణాంకము
(B) a కి q కారణాంకము
(C) A మరియు B
(D) b కి q కారణాంకము
జవాబు.
(C) A మరియు B

ప్రశ్న 60.
\(\frac{21}{25}\) యొక్క దశాంశ రూపంను తెల్పండి.
(A) 0.8
(B) 8.4
(C) 0.48
(D) 0.84
సాధన.
(D) 0.84

వివరణ
\(\frac{21}{25}\) = \(\frac{21}{5^{2}}\) = \(\frac{21 \times 2^{2}}{5^{2} \times 2^{2}}\) = \(\frac{84}{10^{2}}\) = 0.84

ప్రశ్న 61.
\(\frac{23}{2^{3} 5^{2}}\) యొక్క దశాంశ రూపంను భాగహారం చేయకనే రాయండి.
సాధన.
\(\frac{23}{2^{3} \times 5^{2}}\) = \(\frac{23}{2^{3} \times 5^{2}} \times \frac{5}{5}\) = \(\frac{115}{10^{3}}\) = 0.115

ప్రశ్న 62.
\(\frac{129}{2^{3} 5^{2} \times 7^{k}}\) అంతమయ్యే దశాంశము అయిన ఓ విలువ ఎంత ?
సాధన.
\(\frac{129}{2^{3} 5^{2} \times 7^{k}}\) అంతమయ్యే దశాంశము అయిన
2³ × 5² × 7^k = 2^m5ⁿ రూపంలో ఉండాలి.
7^k = 1 కావాలి: 7^k = 7⁰
∴ k = 0

ప్రశ్న 63.
క్రింది వానిలో అంతంకాని ఆవర్తన దశాంశము
(A) \(\frac{2019}{2^{2} \times 5^{2}}\)
(B) \(\frac{2020}{2^{3} \times 5}\)
(C) \(\frac{2021}{2^{3} \times 3 \times 5^{2}}\)
(D) \(\frac{2022}{2^{3} \times 3 \times 5}\)
జవాబు.
(C) \(\frac{2021}{2^{3} \times 3 \times 5^{2}}\)

ప్రశ్న 64.
“రెండు కరణీయ సంఖ్యల మొత్తం ఎల్లప్పుడు కరణీయ సంఖ్య కాకపోవచ్చును” ఒక ఉదాహరణతో సమర్థించండి.
సాధన.
2 + √3 మరియు 5 – √3 లు కరణీయ సంఖ్యలు. వీని మొత్తం (2 + √3) + (5 – √3) = 7 ఒక అకరణీయ సంఖ్య.

ప్రశ్న 65.
“రెండు కరణీయ సంఖ్యల భేదం ఎల్లప్పుడు కరణీయ సంఖ్య కాకపోవచ్చును”.
పై ప్రవచనాన్ని ఒక ఉదాహరణతో సమర్థించండి.
సాధన.
3 + √3 మరియు 2 + √3 లు కరణీయ సంఖ్యలు.
వీని భేదం (3 + √3) – (2 + √3)

ప్రశ్న 66.
ఇచ్చిన అకరణీయ సంఖ్యలను వాని దశాంశ రూపానికి జతపరచండి. .

(A) i-c, ii-a, iii-b, iv-d
(B) i-c, ii-d, iii-a, iv-b
(C) i-b, ii-d, iii-a, iv-c
(D) i-b, ii-d, iii-c, iv-a.
జవాబు.
(B) i-c, ii-d, iii-a, iv-b

ప్రశ్న 67.
√3 = \(\frac{3}{\sqrt{3}}\)ను \(\frac{p}{q}\) రూపంలో రాయవచ్చును. కావున √3 అకరణీయ సంఖ్య అని కిరణ్ అంటున్నారు. కిరణ్ వాదనతో నీవు ఏకీభవిస్తావా ? లేదా ? ఎందుకు ?
సాధన.
కిరణ్ వాదనతో ఏకీభవించను.
√3 = \(\frac{3}{\sqrt{3}}\)ను \(\frac{p}{q}\) రూపంలో రాయగలిగినప్పటికి p, qలు రెండూ పూర్ణసంఖ్యలు, q ≠ 0 అయితేనే \(\frac{p}{q}\) అకరణీయ సంఖ్య అవుతుంది. √3 = \(\frac{3}{\sqrt{3}}\) = \(\frac{p}{q}\), q = √3 పూర్ణ సంఖ్య కాదు. కావున √3 అకరణీయ సంఖ్య అనే వాదన సరైనది కాదు.

ప్రశ్న 68.
\(\frac{17}{125}\) యొక్క దశాంశ రూపంలో దశాంశ భాగంలోని అంకెల సంఖ్య ఎంత ?
సాధన.

ప్రశ్న 69.
\(\frac{237}{2^{\mathrm{n}} \times 5^{3}}\) యొక్క దశాంశ రూపం 4 దశాంశ అంకెల తర్వాత అంతమైతే n విలువ ఎంత ?
సాధన.
\(\frac{237}{2^{\mathrm{n}} \times 5^{3}}\) యొక్క దశాంశ రూపం 4 దశాంశ అంకెల తర్వాత అంతమైతే \(\frac{\mathrm{p}}{\mathrm{q}}\) రూపంలో q = 2⁴ × 5³ గా ఉండాలి.
∴ n = 4

ప్రశ్న 70.
log₇7 విలువను తెల్పండి.
జవాబు.
1

ప్రశ్న 71.
\(\frac{\mathrm{p}}{\mathrm{q}}\) (p, q లు సాపేక్ష ప్రధానాంకాలు, q ≠ 0) ను అంతమయ్యే దశాంశంగా రాయగలిగితే q యొక్క రూపంను రాయండి.
జవాబు.
2ⁿ × 5^m, n, m ∈ W

ప్రశ్న 72.
log_a 1 విలువ ఎంత ?
జవాబు.
0

ప్రశ్న 73.
log_a x = b ను ఘాతరూపంలో రాయండి.
జవాబు.
a_b = x

ప్రశ్న 74.
log₃ 9 = x అయిన x విలువ ఎంత ?
సాధన.
log₃ 9 = x ⇒ 3^x = 9 = 3²
∴ x = 2

ప్రశ్న 75.
log_c √c = 2 అయిన 2 విలువను కనుగొనుము.
సాధన.
log_c √c = log_c c^1/2 = \(\frac{1}{2}\)log_cc = \(\frac{1}{2}\)(1) = \(\frac{1}{2}\)
(లేదా)
log_c √c = x అనుకొనుము.
c^x = √c ⇒ c^x = c^1/2
∴ x = \(\frac{1}{2}\)

ప్రశ్న 76.
2 log 3 + log 5 = log N అయిన N విలువను కనుగొనుము.
సాధన.
2 log 3 + log 5 = log N
= log 3² + log 5
= log 9 + log 5
= log 45 = log N [∵ log m + log n = log mn]
∴ N = 45

ప్రశ్న 77.
log_a324 = 2 అయిన a విలువ ఎంత ?
సాధన.
log_a324 = 2 అయితే a² = 324 = 18²
∴ a = 18.
(లేదా)
log_a324 = 2
⇒ log_a 18² = 2
⇒ 2 log_a 18 = 2
⇒ log_a 18 = \(\frac{2}{2}\) = 1
⇒ log_a 18 = 1
∴ a = 18 (∵ log_aa = 1)

ప్రశ్న 78.
log_x√x = k + 3 అయిన ఓ విలువ ఎంత ?
సాధన.

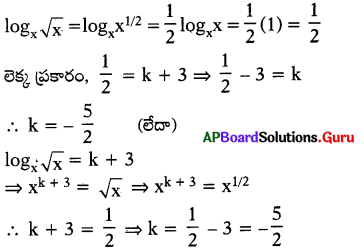
ప్రశ్న 79.
log x²y^m24 = 2 log x + 5 log y + 4 log z అయిన m విలువ ఎంత ?
సాధన.
log x²y^m24 = 2 log x + 5 log y + 4 log z
= log x² + log y⁵ + log z⁴
(∵ log x^m = m log x)
= log x² ∙ y⁵ ∙ z⁴
∴ m = 5

ప్రశ్న 80.
కింది వానిలో ఏది సత్య౦ ?
(A) log₈64 = 2
(B) log₄64 = 3
(C) log₂64 = 4
(D) log₂64 = 6
సాధన.
(C) log₂64 = 4

ప్రశ్న 81.
log_2/3 x = 3 అయిన x విలువ ఏంత?
సాధన.
log_2/3 x = 3 ⇒ \(\left(\frac{2}{3}\right)^{3}\) = x
∴ x = \(\frac{8}{27}\)

ప్రశ్న 82.
log₃ 27√3 విలువను కనుగోనుము.
సాధన.
log₃ 27√3 = log₃3³ × 3^1/2 = log₃3^{3 + 1/2}
= log₃3^7/2 = \(\frac{7}{2}\) log₃3 = \(\frac{7}{2}\)(1) = \(\frac{7}{2}\)
∴ x = \(\frac{7}{2}\)

ప్రశ్న 83.
log₁₀ 25 + log₁₀4 = 2 అని చూపుము.
సాధన.
log₁₀ 25 + log₁₀4 = log₁₀25 × 4
[∵ log x + log y = log xy]
= log₁₀100
= log₁₀10²2
= 2 log₁₀10 = 2

ప్రశ్న 84.
log x + log y = log (x + y) అయిన x ను y లో తెలపండి
సాధన.
log x + log y = log (x + y)
∴ log xy = log (x + y)
∴ xy = x + y
⇒ xy – x = y
⇒ x(y – 1) = y
∴ x = \(\frac{y}{y-1}\)

ప్రశ్న 85.
log₃27 + log₂16 = 7 అని చూపుము.
సాధన.
log₃27 + log₂16 = log₃3³ + log₂2⁴
(∵ log x^m = m log x)
= 3 log₃3 + 4 log₂2
= 3(1) + 4(1)
= 3 + 4 = 7

ప్రశ్న 86.
log (x + 1) – log (x – 1) = log\(\frac{5}{4}\) అయిన x విలువను గణించండి.
సాధన.
log (x + 1) – log (x – 1) = log\(\frac{5}{4}\)
log\(\left(\frac{x+1}{x-1}\right)\) = log\(\frac{5}{4}\) [∵ logx – log y = log\(\frac{x}{y}\)]
∴ \(\frac{x+1}{x-1}\) = \(\frac{5}{4}\)
⇒ 5x – 5 = 4x + 4
⇒ 5x – 4x = 4 + 5 = 9
∴ x = 9

ప్రశ్న 87.
క్రింది వానిలో ఏది సత్యం ?
(A) ఏ శూన్యేతర ఆధారానికైనా ఒకటి సంవర్గమానం సున్న.
(B) ఏ శూన్యేతర ఆధారానికైనా ఒక సంఖ్య సంవర్గ మానం అదే సంఖ్య ఆధారానికి 1 అవుతుంది.
(C) ఒక సంఖ్య సంవర్గమానాలు వేర్వేరు ఆధారాలకు వేర్వేరుగా ఉంటాయి.
(D) పైవి అన్నీ
జవాబు.
D) పైవి అన్నీ

ప్రశ్న 88.
log 30 ని క్రింది ఏ రూపంలో రాయలేము?
(A) log 15 + log 2
(B) log 20 + log 10
(C) log 60 – log 2
(D) log 5 + log 6
జవాబు.
(B) log 20 + log 10

ప్రశ్న 89.
\(\log _{\sqrt{6}}\) 216 విలువను కనుగొనుము.
సాధన.
\(\log _{\sqrt{6}}\) 216 = x అనుకొనుము.
(√6)^x = 216
⇒ 6^x/2 = 6³
⇒ \(\frac{x}{2}\) = 3
∴ x = 6

ప్రశ్న 90.
log₅(x² + 9) = 2 అయిన x విలువ ఎంత ?
సాధన.
logs(x² + 9) = 2 ⇒ 5² = x² + 9
∴ x² + 9 = 25 ⇒ x² = 25 – 9 = 16
∴ x = √16 = ± 4

ప్రశ్న 91.
log 6⁴ = 4 log 6. ఈ సూక్ష్మీకరణలో వాడిన సూత్రాన్ని రాయండి.
జవాబు.
log x^m

ప్రశ్న 92.
log (x – 1) + log (x + 1) = log 24 అయిన X విలువ ఎంత ?
సాధన.
log (x – 1) + log (x + 1) = log 24
log (x – 1) (x + 1) = log 24
∴ (x – 1) (x + 1) = 24
⇒ x² – 1 = 24 ⇒ x² = 25
∴ x = √25 = ± 5

ప్రశ్న 93.
3^log₃x = 4 అయిన X విలువ ఎంత ?
సాధన.
3^log₃x = 4 అయిన x = 4 (∵ a^log_ax = x)
(లేదా)
3^log₃x = 4 ను సంవర్గమాన రూపంలో రాయగా
log₃4 = log₃ x (∵ a^m = x ⇒ log_ax = m)
∴ x = 4

ప్రశ్న 94.
log₃3√3 విలువ ఎంత ?
సాధన.
log₃3√3 = x అనుకొనుము.
3^x = 3√3 = 3^3/2
∴ x = \(\frac{3}{2}\)

ప్రశ్న 95.
జతపరుచుము:

(A) i-d, ii-a, iii-c, iv-b
(B) i-d, ii-b, iii-a, iv-c
(C) i-d, ii-c, iii-b, iv-a
(D) i-c, ii-d, iii-b, iv-a
జవాబు.
(C) i-d, ii-c, iii-b, iv-a

ప్రశ్న 96.
log₈2 = y అయిన y విలువను కనుగొనుము.
సాధన.
log₈2 = y
⇒ 8^y = 2 ⇒ (2³)y = 2 ⇒ 2^3y = 2¹
∴ 3y = 1 ⇒ y = \(\frac{1}{3}\)

ప్రశ్న 97.
సహజ సంవర్గమానం యొక్క ఆధారము
(A) e
(B) π
(C ) 10
(D) 1
జవాబు.
(A) e

ప్రశ్న 98.
log 10 + 2 log 3 – log 2 ను ఒకే సంవర్గమానంగా రాయండి.
సాధన.
log 10 + 2 log 3 – log 2
= log 10 + log 32 – log 2
= log 10 + log 9 – log 2
= log \(\frac{10 \times 9}{2}\) = log 45

ప్రశ్న 99.
జతపరుచుము:

(A) i-c, ii-b, iii-a
(B) i-a, ii-b, iii-c
(C) i-b, ii-c, iii-a
(D) i-b, ii-a, iii-c
జవాబు.
(A) i-c, ii-b, iii-a

ప్రశ్న 100.
log₂ 16 – log₂ 4 = 2 అని చూపుము.
సాధన.
log₂ 16 – log₂ 4 = log₂\(\frac{16}{4}\)
(∵ log x – log y = log \(\frac{x}{y}\))
= log₂ 4
= log₂2²
= 2 log₂ 2 = 2(1) = 2
(∵ log x^m = m log x)

ప్రశ్న 101.
log \(\frac{16}{81}\) = p (log 2 – log 3) అయిన p విలువను కనుగొనుము.
సాధన.
log\(\frac{16}{81}\) = log 16 – log 81
= log 2⁴ – log 3⁴
= 4 log 2 – 4 log 3
= 4 (log 2 – log 3)
∴ 4 (log 2 – log 3) = p(log 2 – log 3)
∴ p = 4.

ప్రశ్న 102.
3² = 9 యొక్క సంవర్గమాన రూపంను రాయండి.
సాధన.
log₃9 = 2

ప్రశ్న 103.
“రెండు కరణీయ సంఖ్యల మొత్తం కరణీయ సంఖ్య కాకపోవచ్చు” అనడానికి క్రింది వానిలో ఏది సరైన ఉదాహరణ ?
(A) √2 + √3
(B) (√2 + √3) + (√2 – √3)
(C) (2 – √3) + (2 + √3)
(D) (2 – 2√3) + (2 + 5√3)
జవాబు.
(C) (2 – √3) + (2 + √3)

ప్రశ్న 104.
“రెండు కరణీయ సంఖ్యల లబ్దం కరణీయ సంఖ్య కాకపోవచ్చు” అని నిరూపించుటకు ఒక ఉదాహరణను ఇవ్వండి.
సాధన.
√2 మరియు 2√2 లు కరణీయ సంఖ్యలు.
వీని లబ్దం √2 × 2√2 = 4 ఒక అకరణీయ సంఖ్య.
(లేదా)
2 – √3 మరియు 2 + √3 లు కరణీయ సంఖ్యలు.
వీని లబ్ధం (2 – √3) (2 + √3)
= 2² – (√3)²
= 4 – 3 = 1 అకరణీయ సంఖ్య.

ప్రశ్న 105.
క్రింది వానిలో ఒకట్ల స్థానంలో సున్నను కలిగి ఉండే సంఖ్య ఏది?
(A) 2³ × 3⁵ × 7
(B) 2⁵ × 3² × 11
(C) 5² × 3³ × 7
(D) 2² × 3 × 5³
జవాబు.
(D) 2² × 3 × 5³
[∵ ‘0’ తో అంతం కావాలంటే ఆ సంఖ్య ప్రధాన కారణాంకాలలో 2 మరియు 5 ఉండాలి.]

ప్రశ్న 106.
log₁₀2 = 0.3010 అయిన log₁₀4 = 0.6020 అని చూపుము.
సాధన.
log₁₀4 = log₁₀2² = 2 log₁₀2
= 2 × 0.3010 = 0.6020

ప్రశ్న 107.
21252 = 3 × 7 × 2² × 23 × 11 = 2² × 7 × p × 11 × 23 అయిన p విలువ ఎంత ?
జవాబు.
p = 3

ప్రశ్న 108.
పై 107వ సమస్యలో pవిలువను కనుగొనుటలో నీవు ఉపయోగించుకొన్న సిద్ధాంతం పేరు రాయండి.
జవాబు.
అంకగణిత ప్రాథమిక సిద్ధాంతము.

ప్రశ్న 109.
4 మరియు 5 ల మధ్యగల ‘ఒక కరణీయ సంఖ్యను రాయండి.
సాధన.
4, 5 ల మధ్యగల కరణీయ సంఖ్య = \(\sqrt{4 \times 5}\) = \(\sqrt{20}\)
(లేదా)
4 = \(\sqrt{16}\), 5 = \(\sqrt{25}\). 4, 5 మధ్యగల కరణీయ సంఖ్యలు \(\sqrt{17}, \sqrt{18}, \sqrt{19}, \sqrt{20}, \sqrt{21}, \ldots . \sqrt{24}\) వీనిలో ఏదేని ఒకటి రాయవచ్చును.
(లేదా)
4, 5 మధ్యగల ఏదేని అంతంకాని ఆవర్తన దశాంశ భిన్నం కూడా కరణీయ సంఖ్య అవుతుంది.
∴ 4, 5ల మధ్యగల కరణీయ సంఖ్యకు ఉదాహరణ
4.52374152932…….. 2

ప్రశ్న 110.
2 log 3 + 3 log 5 – 5 log 2 ను ఒకే సంవర్గ మానంగా రాయడంలో సోపానక్రమాన్ని ఎన్నుకొనుము.
సోపానం (a) : log 1125-log 32
సోపానం (b) : log 9 + log 125 – log 32,
సోపానం (c) : log (9 × 125) – log 32
సోపానం (d) : log \(\frac{1125}{32}\)
సోపానం (e) : log 3² + log 5³ – log 2⁵
(A) b, c, d, a, e
(B) d, e, b, c, a
(C) e, b, c, a, d C
(D) e, a, b, d, c
జవాబు.
(C) e, b, c, a, d C

ప్రశ్న 111.
√5 క్రింది ఏ రెండు సంఖ్యల మధ్య ఉంటుంది ?
(A) 4, 5
(B) 2, 3
(C) 25, 26
(D) 5, 6
జవాబు.
(B) 2, 3
(∵ 2 = √4 , 3 = √9 కావున వీని మధ్య √5 ఉంటుంది.)

ప్రశ్న 112.
క్రింది వానిలో అసత్య వాక్యము .
(A) ప్రతి సంయుక్త సంఖ్యను ప్రధాన కారణాంకాలుగా రాయవచ్చును.
(B) ప్రతి సంయుక్త సంఖ్య ప్రధాన కారణాంకాల లబ్దము ఏకైకము.
(C) సాపేక్ష ప్రధాన సంఖ్యల క.సా.గు వాని లబ్దానికి సమానం.
(D) సాపే ప్రధాన సంఖ్యల గ.సా.కా. 2
జవాబు.
(D) సాపే ప్రధాన సంఖ్యల గ.సా.కా. 2
(∵ సాపేక్ష ప్రధాన సంఖ్యల గ.సా.బా = 1)

ప్రశ్న 113.
రెండు కరణీయ సంఖ్యల భేదం కరణీయ సంఖ్య కాకపోవచ్చు అని చెప్పడానికి క్రింది వానిలో ఏది సరైన ఉదాహరణ ?
(A) (4 + √5) – (6 + √5)
(B) (4 +√5) – (6 – √5)
(C) (√2 + √3) – (√2 – √3)
(D) 2√5 – √5
జవాబు.
(A) (4 + √5) – (6 + √5)

ప్రశ్న 114.
2.\(\overline{6}\) కు సమానమైన అకరణీయ సంఖ్య
(A) \(\frac{7}{3}\)
(B) \(\frac{8}{3}\)
(C) \(\frac{16}{7}\)
(D) \(\frac{17}{7}\)
జవాబు.
(B) \(\frac{8}{3}\)

ప్రశ్న 115.
క్రింది వానిలో ఏది అసత్యం ‘ ?
I) రెండు కరణీయ సంఖ్యల మొత్తం ఎల్లప్పుడూ కరణీయ సంఖ్య
II) రెండు కరణీయ సంఖ్యల లబ్దం ఎల్లప్పుడూ అకరణీయ సంఖ్య
(A) I మాత్రమే
(B) II మాత్రమే
(C) I మరియు II
(D) పైవి ఏవీకావు
జవాబు.
(C) I మరియు II

ప్రశ్న 116.
a, bలు పూర్ణ సంఖ్యలు మరియు a ≠ 0, b # 0, a, bల అన్ని విలువలకు \(\frac{a^{2}+b^{2}}{2 a b}\) ఒక
(A) సంయుక్త సంఖ్య
(B) అకరణీయ సంఖ్య
(C) ప్రధాన సంఖ్య
(D) కరణీయ సంఖ్య
జవాబు.
(B) అకరణీయ సంఖ్య

ప్రశ్న 117.
\(\frac{1}{4000}\) యొక్క దశాంశ రూపంను రాయండి.
సాధన.

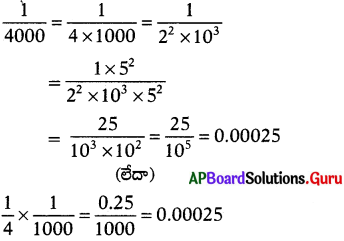
ప్రశ్న 118.
p, qలు సాపేక్ష ప్రధాన సంఖ్యలు, q ≠ 0, అకరణీయ సంఖ్య \(\frac{p}{q}\) కు సంబంధించి క్రింది వానిలో ఏది అసత్యం ? (n, m ∈ W)
(A) q అనేది 10 యొక్క ఘాతసంఖ్య అయితే \(\frac{p}{q}\) అంతమయ్యే దశాంశం.
(B) q = 2ⁿ × 5^m రూపంలో ఉంటే \(\frac{p}{q}\) అంతమయ్యే దశాంశము.
(C) q = 2ⁿ × 5^m రూపంలో ఉంటే \(\frac{p}{q}\) అంతంకాని ఆవర్తన దశాంశము.
(D) q యొక్క ప్రధాన కారణాంకాలలో 2 మరియు 5లతో పాటు ఇతర ప్రధాన కారణాంకాలుంటే \(\frac{p}{q}\) అంతం కాని ఆవర్తన దశాంశము.
జవాబు.
(D) q యొక్క ప్రధాన కారణాంకాలలో 2 మరియు 5లతో పాటు ఇతర ప్రధాన కారణాంకాలుంటే \(\frac{p}{q}\) అంతం కాని ఆవర్తన దశాంశము.

ప్రశ్న 119.
క్రిడిది వానిలో ఒకట్ల స్థానంలో 5ను కలిగి ఉండే సంఖ్య ఏది ?
(A) 2 × 5³ × 3.
(B) 2³ × 3² ×7
(C) 2³ × 5 × 3²
(D) 3² × 5 × 7
జవాబు.
(D) 3² × 5 × 7

ప్రశ్న 120.
a = bq + r అయ్యే విధంగా a = 29, b = 6 అయిన a, r లను కనుగొనుము.
సాధన.
a = 29, b = 6 ⇒ 29 = 6 × 4 + 5
a = bq + r
∴ q = 4, r = 5

ప్రశ్న 121.
p, q లు పూర్ణ సంఖ్యలు, q ≠ 0, \(\frac{\mathbf{p}}{\mathbf{q}}\) రూపంలో రాయలేని వాస్తవ సంఖ్యలను ….. సంఖ్యలు అంటారు.
జవాబు.
కరణీయ

ప్రశ్న 122.
a = 42, b = 8 అయితే a విలువను a = bq + r రూపంలో తెల్పండి.
సాధన.
a = 42, b = 8.
∴ 42 = 8 × 5 + 2

ప్రశ్న 123.
0.00025 = \(\frac{25}{10^{x}}\) అయిన x విలువ ఎంత ?
సాధన.
0.00025 = \(\frac{25}{10^{5}}\) = \(\frac{25}{10^{x}}\)
∴ x = 5

ప్రశ్న 124.
క్రింది వానిని ఆరోహణా క్రమంలో రాయండి.
log₂ 4, log₂16, log₂ 8, log₂ 2
సాధన.
log₂ 2, log₂ 4, log₂ 8, log₂ 16
A.P. 10వ తరగతి జీ గణితశాస్త్రం |

ప్రశ్న 125.
0.375ను p, qలు పరస్పర ప్రధానాంకాలుగా \(\frac{\mathrm{p}}{\mathrm{q}}\) రూపంలో రాసిన q విలువ క్రింది వానిలో ఏది కావచ్చును?
(A) 1000
(B) 40
(C) 8
(D) పైవన్నీ
సాధన.
(D) పైవన్నీ

వివరణ
0.375 = \(\frac{375}{1000}\) = \(\frac{15}{40}\) = \(\frac{3}{8}\)
∴ q = 1000, 40, 8 కావచ్చును.

ప్రశ్న 126.
\(\frac{7}{25}\) యొక్క దశాంశ రూపంను రాయండి.
సాధన.
\(\frac{7}{25}\) = \(\frac{7}{5^{2}} \times \frac{2^{2}}{2^{2}}\) = \(\frac{7 \times 4}{10^{2}}\) = \(\frac{28}{10^{2}}\) = 0.28

ప్రశ్న 127.
\(\frac{7218}{2^{2} \times 5^{2}}\) యొక్క దశాంశ రూపంను రాయండి.
సాధన.
\(\frac{7218}{2^{2} \times 5^{2}}\) = \(\frac{7218}{10^{2}}\) = 72.18

ప్రశ్న 128.
\(\frac{36}{2^{3} \times 5^{2}}\) ను దశాంశ రూపంలో తెల్పండి.
సాధన.

ప్రశ్న 129.
3√2 అకరణీయ సంఖ్య కావడానికి గుణించాల్సిన – కనిష్ఠ కరణీయ సంఖ్య ఏది ?
జవాబు.
√2

ప్రశ్న 130.
\(\frac{37}{2^{3} \times 5^{2} \times 7}\) అంతమయ్యే దశాంశం కావడానికి గుణించాల్సిన కనిష్ఠ సంఖ్య ఏది ?
జవాబు.
7

ప్రశ్న 131.
ఒక సహజసంఖ్య 5తో అంతం కావాలంటే దాని ప్రధాన కారణాంకాలలో తప్పక ఉండాల్సిన కారణాంకం ఏది?
జవాబు.
5

ప్రశ్న 132.
16380 యొక్క ప్రధాన కారణాంకాల లబ్ధం 2² × 5 × 7 × p² × 13 అయిన p విలువ ఎంత ?
సాధన.
16380 = 2² × 3² × 5 × 7 × 13
= 2² × 5 × 7 × p² × 13
∴ p = 3
(లేదా)
16380 = 2² × 5 × 7 × p² × 13
∴ \(\frac{16380}{2 \times 5 \times 7 \times 13}=\) = p²
⇒ 9 – p² ⇒ √9 = p
∴ p = 3

ప్రశ్న 133.
log₂₇ 9 = \(\frac{2}{3}\) అని చూపుము.
సాధన.
log₂₇9 = x అనుకొనుము.
∴ 27^x = 9 ⇒ (3³)^x = 3²
⇒ 3^3x = 3² ⇒ 3x = 2
∴ x = \(\frac{2}{3}\)

ప్రశ్న 134.
2 log 3 – 3 log 2 ను ఒకే సంవర్గమానంగా రాయండి.
సాధన.
2 log 3 – 3 log 2 = log 3² – log 2³
= log 9 – log 8 = log \(\frac{9}{8}\)
[∵ log x^m = m log x, log \(\frac{x}{y}\) = log x -logy]

ప్రశ్న 135.
3 log 2 + 2 log 5ను log N రూపంలో తెల్పండి.
సాధన.
3 log 2 + 2 log 5 = log 2³ + log 5²
= log 8 + log 25
= log (8 × 25)
= log 200

ప్రశ్న 136.
log 2 + log 3 ని ఒకే సంవర్గమానంగా రాయండి.
సాధన.
log 6 ( log x + log y = log xy)

ప్రశ్న 137.
log \(\frac{343}{125}\) = k(log 7 – log 5) అయిన ఓ విలువ ఎంత ?
సాధన.
log \(\frac{343}{125}\) = log \(\left(\frac{7}{5}\right)^{3}\)
= 3 log \(\frac{7}{5}\) = 3 (log 7 – log 5)
∴ 3 (log 7 – log 5) = k (log 7 – log 5)
∴ k = 3

ప్రశ్న 138.
\(\log _{\sqrt{2}}\) 4 విలువను కనుగొనుము.
సాధన.
\(\log _{\sqrt{2}}\) 4 = x అనుకొనుము.
⇒ (√2)^xx = 4 ⇒ 2^x/2 = 2² ⇒ \(\frac{x}{2}\) = 2
∴ x = 4 (లేదా)
\(\log _{\sqrt{2}}\) (√2)⁴ = 4 \(\log _{\sqrt{2}}\) √2 = 4(1) =4

ప్రశ్న 139.
log₅5 మరియు log₅125ల సగటు క్రింది వానిలో దేనికి సమానము ?
(A) log₅25
(B) 2
(C) sec 60°
(D) పైవన్నీ
సాధన.
(D) పైవన్నీ

వివరణ:
log₅5 = 1,
log₅ 125 = log₅ 5³ = 3 log₅ 5 = 3
1, 3ల సగటు = \(\frac{1+3}{2}\) = 2
log₅ 25 = log₅ 5² = 2 log₅ 5 = 2
sec 60° = 2

ప్రశ్న 140.
log 243 + log 1 = log x అయిన X = 243 అని చూపుము.
సాధన.
log 243 + log 1 = log 243 × 1 = log 243
log 243 = log x
∴ x = 243

ప్రశ్న 141.
3 log₅ 4 = log₅ 2^m అయిన m విలువ ఎంత ?
సాధన.
3 log₅ 4 = log₅ 4³
= log₅ 64 = log₅ 2⁶ = log₅ 2^m
∴ m = 6

ప్రశ్న 142.
log 16 – log 2 ను log N రూపంలో రాయగా N విలువ ఎంత?
సాధన.
log 16 – log 2 = log \(\frac{16}{2}\) = log 8
∴ N = 8

ప్రశ్న 143.
log₁₀ 25 + log₁₀ 4 = x² అయిన x విలువ ఎంత?
సాధన.
log ₁₀ 25 + log₁₀ 4
= log₁₀ 100 = log₁₀ 10²
= 2 log₁₀ 10 = 2
∴ 2 = x² ⇒ x = √2

ప్రశ్న 144.
log 100 × log 99 × log 98 × …….. × log 2 × log 1 విలువ ఎంత ?
జవాబు.
0 [∵ log 1 = 0]

ప్రశ్న 145.
\(\log _{\sqrt{7}}\) 343 = x అయిన X విలువ ఎంత ?
సాధన.
\(\log _{\sqrt{7}}\) 343 = x ⇒ (√7)^x = 343
⇒ 7^x/2 = 7³ ⇒ \(\frac{x}{2}\) = 3
∴ x = 6

ప్రశ్న 146.
2^x = y మరియు log₂ y = 3 అయిన (x – y)² విలువను కనుగొనుము.
సాధన.
2^x = y మరియు log₂ y = 3
⇒ log₂ 2^xx = 3 [∵ 2^x = y]
⇒ x log₂ 2 = 3
∴ x(1) = 3 ⇒ x = 3
∴ 2³ = y ⇒ y = 8
(x – y)² = (3 – 8)² = (- 5)² – 25

ప్రశ్న 147.
ఈ క్రింది వానిలో అంతం కాని ఆవర్తన దశాంశము ఏది ?
(A) √4
(B) log₂32
(C) \(\frac{10}{3}\)
(D) \(\frac{3}{10}\)
జవాబు.
(C) \(\frac{10}{3}\)

ప్రశ్న 148.
log₂ 8, log₂ 16 ల క.సా.గు ………………..
(A) log₉ 324
(B) 12
(C) log₂ 2¹²
(D) పైవన్నీ
జవాబు.
(D) పైవన్నీ

ప్రశ్న 149.
a = 4q + r రూపంలో వ్రాయగలిగిన ‘r’ యొక్క గరిష్ఠ సాధ్య విలువ ఎంత ?
జవాబు.
3.

ప్రశ్న 150.
log₁₀ x = k అయిన క్రింది వానిని జతపరుచుము.

(A) i-c, ii-a, iii-b, iv-d
(B) i-d, ii-a, iii-b, iv-c
(C) i-c, ii-b, iii-a, iv-d
(D) i-d, ii-b, iii-a, iv-c
జవాబు.
(D) i-d, ii-b, iii-a, iv-c

ప్రశ్న 151.
x = log₂ 3 మరియు y = log₂ 5 అయిన log₂ 30 ని x, y లలో తెల్పండి.
సాధన.
x = log₂ 30 = log₂ (2 × 3 × 5)
= log₂ 2 + log₂ 3 + log₂ 5
= 1 + x + y

ప్రశ్న 152.
log₁₀ 2 = 0.3010 అయిన log₁₀ 5 విలువను కనుగొనుము.
సాధన.
log₁₀ 5 = log₁₀ \(\left(\frac{10}{2}\right)\)
= log₁₀ 10 – log₁₀ 2
= 1 – 0.3010 = 0.6990

ప్రశ్న 153.
log₅ (x + 5) = 1 అయిన ‘X’ విలువను కనుగొనుము.
సాధన.
log₅ (x + 5) = 1.
⇒ x + 5 = 5 = x = 0

ప్రశ్న 154.
2 log, x = 6 అయిన ‘X’, ‘y’ ల నుధ్య సంబంధమును తెల్పండి.
సాధన.
2 log, x = 6 = log, x = 3
∴ y³ = x

ప్రశ్న 155.
యూక్లిడ్ భాగహార నియమాన్ని ఉపయోగించి 60 మరియు 100 ల గ.సా.భాను కనుగొనడంలో గల సోపానాలను క్రమంలో అమర్చండి.
సోపానం (i) : 60 = 40(1) + 20
సోపానం (ii) : 100 = 60(1) + 40
సోపానం (iii) : 40 = 20(2) + 0
సోపానం (iv) : 60, 100 ల గ.సా.భా – 20
(A) (i), (ii), (iii), (iv)
(B) (ii), (i), (iii), (iv)
(C) (ii), (iv), (iii), (i)
(D) (iii), (ii), (iv), (i)
జవాబు.
(B) (ii), (i), (iii), (iv)

ప్రశ్న 156.
log (x² – 1) – log (x + 1) = log 9 అయిన ‘x’ విలువ ఎంత ?
సాధన.
log (x² – 1) – log (x + 1) = log 9 .
log\(\left(\frac{x^{2}-1}{x+1}\right)\) = log 9

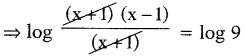
⇒ x – 1 = 9
∴ x = 10

ప్రశ్న 157.
a = bq + r నందు a = 80, b = 10 అయినపుడు q + r విలువ ఎంత?
సాధన.
80 = 10 × 8 + 0
a = bq + r, q = 8, r = 0
∴ q + r = 8 + 0 = 8

ప్రశ్న 158.
log₃ 729 విలువను కనుగొనుము.
సాధన.
log₃ 729 = log₃ 3⁶ = 6 log₃3 = 6

ప్రశ్న 159.
√p అనునది ఒక ప్రధాన సంఖ్య అయిన p యొక్క కనీస విలువ ఎంత ?
జవాబు.
2

ప్రశ్న 160.
ప్రవచనం I: \frac{13}{2^{3} \times 5}\(\) యొక్క దశాంశరూపం అంతమయ్యే దశాంశం అవుతుంది.
వివరణ (II): n, m లు రుణేతర పూర్ణసంఖ్యలు మరియు q యొక్క ప్రధాన కారణాంకాల లబ్దం 2ⁿ × 5^m రూపంలో ఉంటే అకరణీయ సంఖ్య
x = \(\frac{\mathrm{P}}{\mathrm{q}}\) అయిన x యొక్క దశాంశ రూపం అంతమయ్యే డశాంశం అవుతుంది.
(A) I మరియు II లు రెండూ సత్యం, I & II సరైన వివరణ
(B) I సత్యం, II అసత్యం , I & II సరైన వివరణ
(C) I అసత్యం , II సత్యం , I కి II సరైన వివరణ
(D) I అసత్యం , II అసత్యం , I & II సరైన వివరణ కాదు
జవాబు.
(A) I మరియు II లు రెండూ సత్యం, I & II సరైన వివరణ

ప్రశ్న 161.
\(\left(a^{1 / x}=\frac{1}{p}\right)\) యొక్క సంవర్గమాన రూపం …………
(A) log_a p = \(\frac{-1}{\mathrm{X}}\)
(B) log_a \(\frac{1}{\mathrm{p}}\) = \(\frac{1}{\mathrm{x}}\)
C) ‘A’ మరియు ‘B’
(D) ఏదీకాదు
సాధన.
C) ‘A’ మరియు ‘B’

వివరణ:

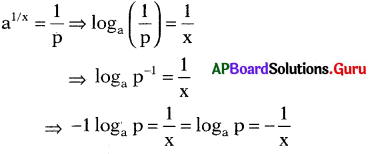
ప్రశ్న 162.
2².3⁴.4² మరియు 2^x.3³.4⁵ ల గసాభా 2².3⁴.4² అయిన X విలువ ………………
(A) 2
(B) 22
(C) ≤ 2
(D) చెప్పలేము
జవాబు.
(B) 22

ప్రశ్న 163.
\(\log _{\sqrt{y}}\) y = x² అయిన x ను కనుగొనుము.
సాధన.

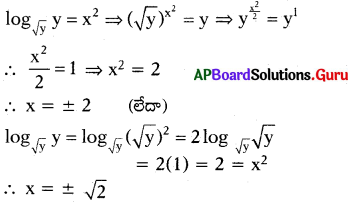
ప్రశ్న 164.
ఈ క్రింది వానిలో సత్యమేది ?
(A) ఋణ సంఖ్యల సంవర్గమానం ఋణాత్మకం
(B) కొన్ని సంఖ్యల సంవర్గమానం విలువ ఋణాత్మకం కావచ్చు
(C) అన్ని ధన సంఖ్యల సంవర్గమానం విలువ ధనాత్మకం
(D) పైవన్నీ
జవాబు.
(B) కొన్ని సంఖ్యల సంవర్గమానం విలువ ఋణాత్మకం కావచ్చు

ప్రశ్న 165.
మొదటి 3 ప్రధాన సంఖ్యల కసాగును రాయండి.
సాధన.
మొదటి 3 ప్రధాన సంఖ్యల క.సా.గు
= 2 × 3 × 5 = 30

ప్రశ్న 166.
ఈ క్రింది వానిలో అకరణీయ సంఖ్య –
(A) log₁₀1
(B) log₁₀10
(C) log₁₀₀10
(D) పైవన్నీ
జవాబు.
(D) పైవన్నీ

ప్రశ్న 167.
aⁿ యొక్క ఫలిత సంఖ్య యొక్క ఒకట్ల స్థానంలో ‘1’ ఉండవలెనన్న ‘a’ యొక్క సాధ్య విలువ
(A) 1
(B) 3
(C) 7
(D) పై వానిలో ఏదైనా ఒకటి
జవాబు.
(D) పై వానిలో ఏదైనా ఒకటి

ప్రశ్న 168.
2, 3 మధ్యగల కరణీయ సంఖ్య …………
(A) √5
(B) √6
(C) √7
(D) పైవన్నీ
జవాబు.
(D) పైవన్నీ

ప్రశ్న 169.
log₅x = y యొక్క ఘాత రూపంను రాయండి.
జవాబు.
5^y = x

ప్రశ్న 170.
log_{sin 30} tan 45 = 0 అని చూపుము.
సాధన.
log_{sin 30} tan 45 = log_1/2 1 = 0 (∵ log_a 1 = 0)

ప్రశ్న 171.
\(\frac{1}{\log _{a} 9}\) = 0.5 అయిన ‘a’ విలువను కనుగొనుము.
సాధన.
\(\frac{1}{\log _{a} 9}\) = 0.5 = \(\frac{1}{2}\)
⇒ log_a 9 = 2 ⇒ a² = 9 = 3² ⇒ a = 3

ప్రశ్న 172.
0.45 యొక్క \(\frac{\mathbf{p}}{\mathbf{q}}\) రూపంను రాయండి.
సాధన.
0.45 = \(\frac{45}{100}\) = \(\frac{9}{20}\)

ప్రశ్న 173.
\(\left(\log _{81} \sqrt{3^{16}}\right)\) విలువ ఎంత ?
సాధన.

ప్రశ్న 174.
log_o.50.0625 విలువ ఎంత?
సాధన.
log_o.50.0625 = log_0.5 (0.5)⁴
= 4 log_0.5 0.5 = 4
(లేదా)

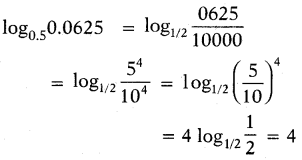
ప్రశ్న175.
log₉ 4. log₉ 3. log₉ 2. log₉ 1 విలువ ఎంత ?
జవాబు :
0 (∵ log_a 1 = 0)

ప్రశ్న176.
ఈ క్రింది వానిలో సంయుక్త సంఖ్య ___________
A) 7 × 11 + 11
B) 7 × 11 × 13 + 13
C) 7 × 11 × 13 × 15
D) పైవన్నీ
జవాబు :
D) పైవన్నీ

ప్రశ్న177.
ఏదైనా పూర్ణ సంఖ్య వర్గం ___________ రూపంలో ఉండును.
A) 4p
B) 4p + 1
C) 4p + 2
D) ‘A’ లేదా ‘B’
జవాబు :
D) ‘A’ లేదా ‘B’

ప్రశ్న178.
x = 2, q ≠0. \(\frac{p}{q}\) కనిష్ఠ రూపంలో
q = 2^m × 3ⁿ × 5^r, n ≠ 0 అయిన x గురించి నీవు ఏమి చెప్పగలవు ?
A) అంతమగు దశాంశము
B) అంతంకాని. ఆవర్తన దశాంశము
C) కరణీయ సంఖ్య
D) సహజ సంఖ్య
జవాబు :
B) అంతంకాని. ఆవర్తన దశాంశము

ప్రశ్న179.
log (sin θ) + log (cosec θ) విలువ ఎంత ?
జవాబు :
log (sin θ) + log (cosec θ)
= log sin θ × cosec θ [∵ log x + log y = log xy]
= log(sin θ × \(\frac{1}{\sin \theta}\))
= log (1) = 0

ప్రశ్న180.
log (tan θ) + log (cosec θ) + log (cos θ) = 0 అని చూపుము.
జవాబు :
log (tan θ) + log (cosec θ) + log (cos θ) = log (tan θ . cosec θ . cos θ)
[: log x + log y + log z = log (xyz)]

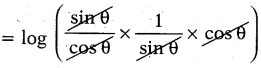
= log (1) = 0

ప్రశ్న181.
log_2/3 \(\left(\frac{27}{8}\right)\) విలువ ఎంత ?
జవాబు :
– 3

ప్రశ్న182.
ఆకరణీయ సంఖ్య \(\frac{7}{2^{2} \times 5}\) యొక్క దశాంశ రూపం రాయండి.
జవాబు :
0.35

ప్రశ్న183.
log_3√5 √5 యొక్క విలువ ఎంత ?
జవాబు :

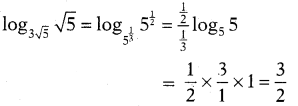
ప్రశ్న184.
ఏ వాక్యముతో నీవు ఏకీభవిస్తావు ?
P : రెండు కరణీయ సంఖ్యల లబ్దం ఎల్లప్పుడూ – అకరణీయ సంఖ్యే.
Q : అకరణీయ మరియు కరణీయ సంఖ్యల లబ్దం ఎల్లప్పుడూ కరణీయ సంఖ్య.
i) P మాత్రమే
ii) Q మాత్రమే
iii) P మరియు Q
జవాబు :
ii) Q మాత్రమే

ప్రశ్న185.
3 log_2 = x ను ఘాతరూపంలో వ్రాయుము.
జవాబు :
3 log₂ 2 = x
log₂2₃ = x ⇒ log₂ 8 = x ⇒ 2_x = 8