AP Board 10th Class Maths Solutions Chapter 14 సాంఖ్యకశాస్త్రం Exercise 14.2

SCERT AP 10th Class Maths Textbook Solutions Chapter 14 సాంఖ్యకశాస్త్రం Exercise 14.2 Textbook Exercise Questions and Answers.

AP State Syllabus 10th Class Maths Solutions 14th Lesson సాంఖ్యకశాస్త్రం Exercise 14.2

ప్రశ్న 1.
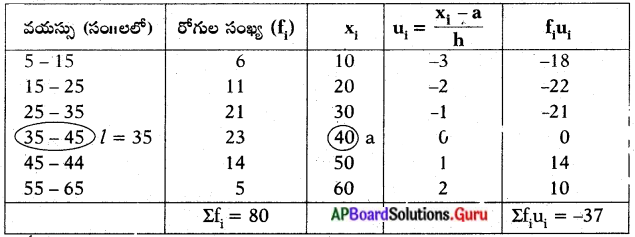
ఒక సంవత్సర కాలంలో, ఒక వైద్యశాలలో చేరిన రోగుల యొక్క వయస్సుల వివరాలు ఈ క్రింది పట్టికలో ఇవ్వబడినాయి.

పై దత్తాంశానికి సగటు మరియు బాహుళకాలను కనుగొనుము. అదేవిధంగా అట్టి కేంద్ర స్థాన విలువలను పోల్చి వ్యాఖ్యానించుము.
సాధన.

దత్తాంశం యొక్క బాహుళకము (Z) = l + [latex]\frac{\left(f_{1}-f_{0}\right)}{2 f_{1}-\left(f_{0}+f_{2}\right)}[/latex] × h
l = బాహుళక తరగతి యొక్క దిగువ హద్దు = 35
h = బాహుళక తరగతి పొడవు = 10
f = బాహుళక తరగతి యొక్క పౌనఃపున్యము = 23
f₁ = బాహుళక తరగతి ముందున్న తరగతి యొక్క పౌనఃపున్యము = 21
f₀ = బాహుళక తరగతికి తరువాత నున్న తరగతి యొక్క పౌనఃపున్యము = 14
బాహుళకము = l + [latex]\frac{\left(f_{1}-f_{0}\right)}{2 f_{1}-\left(f_{0}+f_{2}\right)}[/latex] × h
= 35 + [latex]\frac{23-21}{2 \times 23-(21+14)}[/latex] × 10
= 35 + [latex]\frac{20}{11}[/latex]
= 35 + 1.81 = 36.81
∴ బాహుళకము = 36.81 సం॥
సగటు ([latex]\overline{\mathbf{x}}[/latex]) = a + [latex]\frac{\Sigma \mathrm{f}_{\mathrm{i}} \mathrm{u}_{\mathrm{i}}}{\Sigma \mathrm{f}_{\mathrm{i}}}[/latex] × h
a = 40
Σf_iu_i = – 37
Σf_i = 80
h = 10
∴ సగటు ([latex]\overline{\mathbf{x}}[/latex]) = a + [latex]\frac{\Sigma \mathrm{f}_{\mathrm{i}} \mathrm{u}_{\mathrm{i}}}{\Sigma \mathrm{f}_{\mathrm{i}}}[/latex] × h
= 40 + [latex]\frac{-37}{80}[/latex] × 10
= 40 – [latex]\frac{37}{8}[/latex]
= 40 – 4.625 = 35.375
∴ ఒక సంవత్సర కాలంలో, ఒక వైద్యశాలలో చేరిన రోగుల యొక్క వయస్సు సగటు ([latex]\overline{\mathbf{x}}[/latex]) = 35.375సం||

వ్యాఖ్యానం :
ఒక వైద్యశాలలో చేరిన ఎక్కువ మంది యొక్క వయస్సు 36.8 సం||. కానీ సరాసరి వైద్యశాలలో చేరిన వారి వయస్సు 35.37 సం||. ఇక్కడ సగటు బాహుళకము కన్నా తక్కువగా ఉన్నది.

ప్రశ్న 2.
ఈ క్రింది పట్టికలో 225 విద్యుత్ పరికరాల జీవితకాల (గంటలలో) వివరాలు ఇవ్వబడినాయి. . . . జీవితకాలం

పై విద్యుత్ పరికరాల జీవితకాల బాహుళకాన్ని కనుగొనుము.
సాధన.

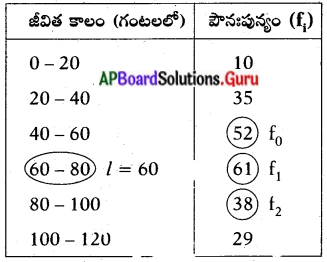
l = బాహుళక తరగతి యొక్క దిగువహద్దు = 60
h = బాహుళక తరగతి పొడవు = 20 .
f₁ = బాహుళక తరగతి యొక్క పౌనఃపున్యము = 61
f₀ = బాహుళక తరగతి ముందున్న తరగతి యొక్క పౌనఃపున్యము = 52
f₂ = బాహుళక తరగతికి తరువాతనున్న తరగతి యొక్క పౌనఃపున్యము = 38
బాహుళకము = l + [latex]\frac{\left(f_{1}-f_{0}\right)}{2 f_{1}-\left(f_{0}+f_{2}\right)}[/latex] × h
= 60 + [latex]\left[\frac{61-52}{2 \times 61-(52+38)}\right][/latex] × 20
= 60 + [latex]\frac{180}{32}[/latex]
= 60 + 5.625
= 65.625
విద్యుత్ పరికరాల జీవితకాల బాహుళకము = 65.625.

ప్రశ్న 3.
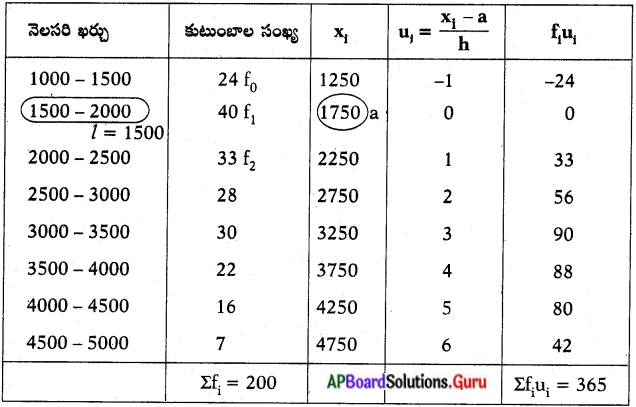
ఒక గ్రామంలోని 200 కుటుంబాల యొక్క నెలసరి ఖర్చుల వివరాలను ఈ క్రింది పౌనఃపున్య విభాజన పట్టికలో ఇవ్వబడినవి. అట్టి కుటుంబాల నెలసరి ఖర్చుల బాహుళకాన్ని కనుక్కోండి. అదే విధంగా నెలసరి సరాసరి ఖర్చును కనుక్కోండి.

సాధన.

బాహుళకము :
l = 1500,
f₁ = 40,
f₀ = 24,
f₂ = 33,
h = 500
∴ బాహుళకము = l + [latex]\frac{\left(f_{1}-f_{0}\right)}{2 f_{1}-\left(f_{0}+f_{2}\right)}[/latex] × h
= 1500 + [latex]\frac{[40-24]}{2 \times 40-(24+33)}[/latex] × 500
= 1500 + [latex]\frac{16 \times 500}{23}[/latex]
= 1500 + [latex]\frac{8000}{23}[/latex]
= 1500 + 347.82
= 1847.32
∴ బాహుళకము = ₹1847.82.
ఊహించిన సగటు (a) = 1750
∴ సగటు ([latex]\overline{\mathbf{x}}[/latex]) = a + [latex]\frac{\Sigma \mathrm{f}_{\mathrm{i}} \mathrm{u}_{\mathrm{i}}}{\Sigma \mathrm{f}_{\mathrm{i}}}[/latex] × h
= 1750 + [latex]\frac{365}{200}[/latex] × 500
= 1750 + [latex]\frac{365 \times 5}{2}[/latex]
= 1750 + 912.5
= ₹ 2662.5
ఇచ్చిన దత్తాంశం యొక్క బాహుళకం = ₹ 1847.83,
నెలసరి సరాసరి ఖర్చు = ₹ 2662.5.

ప్రశ్న 4.
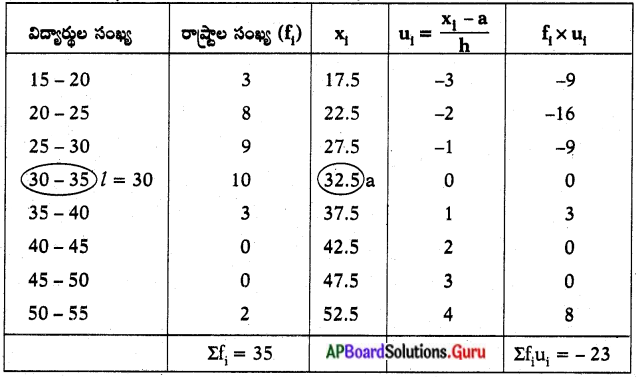
రాష్ట్రాల వారీగా సెకండరీ పాఠశాలల్లో గల ఉపాధ్యాయ – విద్యార్థి నిష్పత్తి విలువలను ఈ క్రింది పౌనఃపున్య విభాజన పట్టికలో ఇవ్వడమైనది. ఇట్టి దత్తాంశానికి బాహుళకాన్ని మరియు సగటును గణించండి. మరియు ఈ రెండు కేంద్రస్థాన విలువలపై వ్యాఖ్యానించుము.

సాధన.

బాహుళకము :
l = 30, f₁ = 9, f₀ = 10, f₂ = 3, h = 5.
∴ బాహుళకము = l + [latex]\frac{\left(f_{1}-f_{0}\right)}{2 f_{1}-\left(f_{0}+f_{2}\right)}[/latex] × h
= 30 + [latex]\frac{[10-9]}{20-12}[/latex] × 5
= 30 + [latex]\frac{5}{8}[/latex]
= 30 + 0.625
∴ బాహుళకము = 30.625.

సగటు:
Σf_i = 35
Σf_iu_i = – 23
a = 32.5, h = 5
∴ సగటు ([latex]\overline{\mathbf{x}}[/latex]) = a + [latex]\frac{\Sigma \mathrm{f}_{\mathrm{i}} \mathrm{u}_{\mathrm{i}}}{\Sigma \mathrm{f}_{\mathrm{i}}}[/latex] × h
= 32.5 + [latex]\frac{-23}{35}[/latex] × 5
= 32.5 – [latex]\frac{23}{7}[/latex]
= 32.5 – 3.28
= 29.21.
∴ ఇచ్చిన దత్తాంశం యొక్క బాహుళకం = 30.6,
∴ సగటు = 29.21.
వ్యాఖ్యానం :
బాహుళకము ప్రకారం ఉపాధ్యాయ విద్యార్థి నిష్పత్తి 30.6 కానీ సరాసరి విలువ 29.2 గా గలదు.

ప్రశ్న 5.
వన్డే క్రికెట్ మ్యాచుల్లో ప్రపంచంలో అత్యున్నత శ్రేణి బ్యాట్స్మ న్లు సాధించిన పరుగుల వివరాలను ఈ క్రింది పౌనఃపున్య విభాజన పట్టికలో ఇవ్వడమైనది.

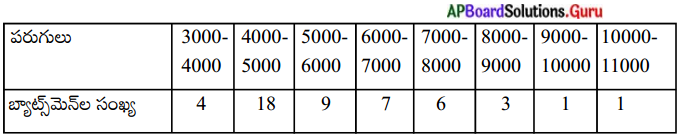
పై దత్తాంశమునకు బాహుళకాన్ని కనుగొనుము
సాధన.

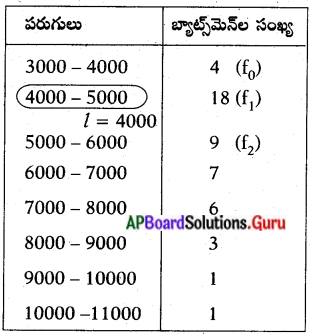
పరుగులు బ్యాట్స్మన్ల సంఖ్య
∴ l = 4000, f₀ = 4, f_` = 18, f₂ = 9,.
h = 1000 (f) (4000 – 5000) 18 (f)
∴ బాహుళకం = l + [latex]\frac{\left(f_{1}-f_{0}\right)}{2 f_{1}-\left(f_{0}+f_{2}\right)}[/latex] × h
= 4000 + [latex]\frac{18-4}{2 \times 18-[9+4]}[/latex] × 1000
= 4000 + [latex]\frac{14000}{23}[/latex]
= 4000 + 608.69
= 4608.69
∴ బాహుళకము = 4608.7 పరుగులు.

ప్రశ్న 6.
ఒక విద్యార్థి, రోడ్డుపై ఒక స్థానం నుంచి వెళ్ళుచున్న కార్ల సంఖ్యను ప్రతి మూడు నిమిషాలకు ఒకసారి (1 పీరియడ్), 100 పీరియడ్ లో లెక్కించి, వివరాలను ఈ క్రింది పట్టికలో క్రోడీకరించాడు.

పై దత్తాంశానికి “బాహుళకాన్ని” కనుక్కోండి.
సాధన.

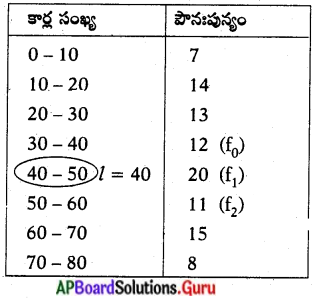
l = 40, f₁ = 20, f₀ = 12, f₂ = 11, h = 10
∴ బాహుళకము = l + [latex]\frac{\left(f_{1}-f_{0}\right)}{2 f_{1}-\left(f_{0}+f_{2}\right)}[/latex] × h
= 40 + [latex]\frac{(20-12)}{2 \times 20-(12+11)}[/latex] × 10
= 40 + [latex]\frac{80}{17}[/latex]
= 40 + 4.7
44.7
బాహుళకము = 44.7 కార్లు.